海洋平台气泡幕降噪性能及影响因素

储乐平， 李 巍， 赵瑞云， 刘 松， 张苏飞， 李 楷， 王延林， 石艳芳

(1. 海洋石油工程股份有限公司， 天津 300451；2. 大连理工大学 船舶工程学院， 辽宁 大连 116024；3. 大连理工大学 海洋科学与技术学院， 辽宁 盘锦 124221)

0 引 言

在海洋平台桩腿上设置气泡幕降噪系统，用以降低打桩噪声，避免对施工区域附近的海豚、白鳍豚等海生物的栖息活动造成影响。气泡幕降噪系统由压缩机、压缩空气分配/控制/显示单元、气泡发生管等3部分组成，其工作原理是压缩空气经过气泡发生管后产生大量气泡，气泡与海水混合形成一个气泡与水的混合帷幕(气泡幕)，利用声音在不同介质间传播的衰减特性起到降噪的作用。

20世纪70年代以来，西方发达国家海军的大中型反潜水面舰艇相继引入气泡幕降噪系统，美国海军称其为“Masker”系统。1990年，王虹斌等[1]分析“Masker”系统及其设计思想，说明降噪系统的布置与舰艇的使命任务、总体布置、经济代价、战斗使用准则等息息相关，并针对不同的舰艇需要指定合理的布置措施。蒋兴舟等[2]和庄宏业[3]均通过水洞试验验证气泡幕在鱼雷航行过程中不仅能提高螺旋桨压力，而且能减少空泡，降低辐射噪声与自噪声。2005年，王虹斌等[4]以水池船模为试验对象，采用控制变量法研究喷气管布置方式、喷孔直径、喷气量等因素对船模降噪效果的影响，试验结果表明为了得到最佳降噪效果，对喷气环布置方式、喷气环与发射器声源之间的相对位置、喷孔直径分布、船速和最佳喷气量进行控制都是必不可少的。同年，该团队以特种舰艇模型为试验对象，再一次验证气泡幕对其具有良好的降噪效果，可见气泡幕降噪具有非常高的实用性和经济价值。

近些年，气泡幕降噪技术已逐渐从军事领域转向海洋工程领域。海洋中生物活动、风力作用、机械运动都会产生大量气泡，气泡群是水中的强散射体，其对透过的声波有很强的衰减和散射作用。孙佳伟[5]通过试验研究水下气泡幕的声透射特性，对气泡幕降噪原理进行深层次分析。苗天丞[6]将试验分析与数值模拟相结合，系统研究浸没式排气的流动与噪声变化规律，并从浸没式排气噪声产生机理出发提出多种降噪方案。韩蕊[7]基于边界积分法(Boundary Integral Method，BIM)建立多气泡非线性耦合数值模型，解决三维气泡融合、多个环状气泡耦合作用等问题，并对水幕反导、大尺度爆炸中气泡的生长过程进行分析。刘竞婷[8]针对水下排气过程，采用理论、数值模拟、试验相结合的方式，对气液两相流流动状态的演化过程和辐射声学特性进行研究，提供水下排气噪声预报方法，为解决工程上的噪声问题提供思路。

与此同时，国外研究者也在对气泡幕的降噪性能进行研究。GIMALTDINOV等[9]研究甲烷气体在处于水合物形成过程时对声波的影响，研究发现，在低频区(小于1 kHz)，水合物形成过程对传播速率、衰减系数和波反射值有较大影响，特别是在水合物形成过程中，波的衰减系数增加2个数量级以上。PHAM等[10]研究非线性共振气泡幕对声波的散射，验证2个重要的效应：阵列内的气泡比孤立的气泡具有更大的辐射阻尼；由于气泡-气泡相互作用，可探测到与声源施加的声压不同的压力。BRYSON等[11]提出一种改进的方法用来预测冲击波产生的峰值入射压力和能流密度，结果表明加入衰减系数后的衰减方程与实测数据吻合较好。

本文在前人研究的基础上，以海洋平台气泡发生管为对象，研究气泡发生管的喷孔数量、排列方式、孔径、通气量对最终形成的气泡幕的体积分数的影响。

1 计算理论

1.1 简化假设

针对气泡发生管模型的特点，给出2点假设：(1) 忽略2排孔产生气体的相互作用，只研究单排孔的体积分数变化；(2) 将气体与液体相互作用视为三维非稳态过程，喷孔附近属于完全湍流状态。

1.2 气泡幕降噪

声波在水中气泡幕层的衰减主要与气泡幕的混合密度和压缩性有关。

水中气泡幕层混合密度ρ的计算公式为

ρ=(1-α)ρw+αρg

(1)

式中：ρw为水的密度；ρg为空气密度；α为气泡幕内空气体积分数，α计算公式为

(2)

式中：Vg为气泡幕层内空气体积；Vw为气泡幕内水的体积。

水中气泡幕层压缩性β为

β=(1-α)βw+αβg

(3)

式中：βw为水的压缩性；βg为空气压缩性。

对于频率远低于气泡幕层气泡共振频率的声波，其在气泡幕层中的传播速度Cot为

(4)

试验表明：只要水中含少量空气，如α=0.001，在接近水面处，声速从1 500 m/s下降至305 m/s；当α=0.5时，声速最小，Cot=20 m/s[12]。

1.3 计算模型

连续性方程、动量守恒方程和能量守恒方程是流体力学中的3个基本方程，此次计算不涉及能量的交换，因此主要介绍连续性方程和动量守恒方程。针对计算模型的特点，须考虑两相流体(水和空气)间的耦合作用，采用欧拉多相分离流模型，该模型在所有相共用一个压力场时对每个相的质量、动量和能量传输方程进行求解。

湍流流动是日常生活中较常见的现象，如圆柱绕流、大气的流动等通常是湍流状态，湍流的运动状态极其复杂，通常利用计算机对其进行模拟。计算的主要方法包括直接数值模拟(Direct Numerical Simulation，DNS)方法、大涡模拟(Large Eddy Simulation，LES)方法和雷诺平均N-S(Reynolds Average N-S，RANS)方法，前两者受计算力的限制，在复杂工程问题上无法应用。RANS是STAR-CCM+中常用的数值模拟方法，常用的湍流模型包括Spalart-Allmaras(一方程湍流模型)，k-ε和k-ω系列(二方程模型)以及雷诺应力模型(Reynolds Stress Model，RSM)。RSM对层流中各向异性湍流的状况适用性较好，但计算成本较高。二方程模型是最简单的完整湍流模型，常用的二方程模型包括SSTk-ω、Standardk-ω、RNGk-ε、Standardk-ε、Realizablek-ε。

本文使用Standardk-ε湍流模型，该模型引入湍动能k和耗散率，其运输方程为

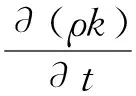
(5)

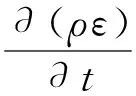
(6)

式(5)和式(6)中：t为时间；μ为流体动力黏度；σk、σε、Cε1、Cε2为模型因数，取值分别为1.00、1.30、1.44、1.92；Pk和Pε分别为浮力和湍流产生项；ε0为抵消湍流衰减的源项；Sk和Sε为用户定义源项；f2为阻尼项；Te和T0为时间尺度项；μt为湍流黏度，其计算公式为

μt=ρCμfμkT

(7)

式中：Cμ为模型因数，取值为0.09；fμ为阻尼项；T为湍流时间尺度。

2 数值预测及分析

2.1 模型建立及网格划分

为计算气泡幕中空气压缩系数和气泡幕混合层密度，需要建立气泡发生管三维模型。截取气泡发生管的一段进行分析以降低计算成本。气泡发生管的计算模型截取长度为1 000 mm，包含5排共20个气泡发生孔，孔间距为200 mm、孔径为2 mm，直列分布，如图1所示。除直列分布外，还有将每排相邻喷孔分别错开50 mm的螺旋状分布，如图2和图3所示。

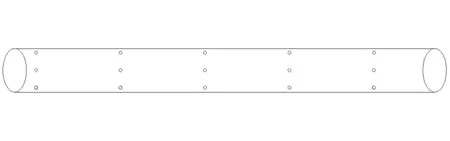
图1 气泡发生管(直列)

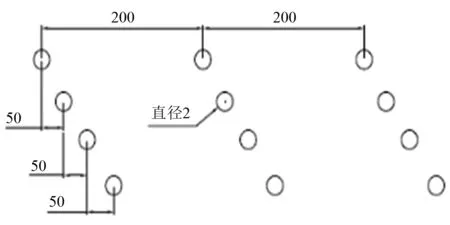
单位：mm图2 螺旋状气泡发生管开孔

图3 气泡发生管(螺旋状)

STAR-CCM+能够划分多种形式的网格，包括四面体、六面体、多面体、柱体等。此次计算利用多面体网格对整个计算域进行网格划分。网格设置相关参数如表1所示。

表1 网格设置

为兼顾计算成本与计算精度，在划分网格时，通过体网格和面网格加密功能，对计算域、气泡发生管周围和喷孔进行局部加密，加密尺寸如表2所示。

表2 网格加密尺寸

2.2 边界条件

计算域模型缩尺比为1∶1，计算域高度为0.70 m、宽度为0.25 m，两侧离气泡发生管距离不等，靠近气泡发生管一侧的距离为0.05 m。边界条件设置为壁面，远离管的一侧设为速度入口，速度为0 m/s，用于模拟无限水域，计算域长度方向根据计算孔数进行修改。计算域模型如图4所示。喷孔设置为速度入口，用于模拟管内气体喷入流域；计算域沿管长方向设为对称边界，上边界设为压力出口，初始相为水相。

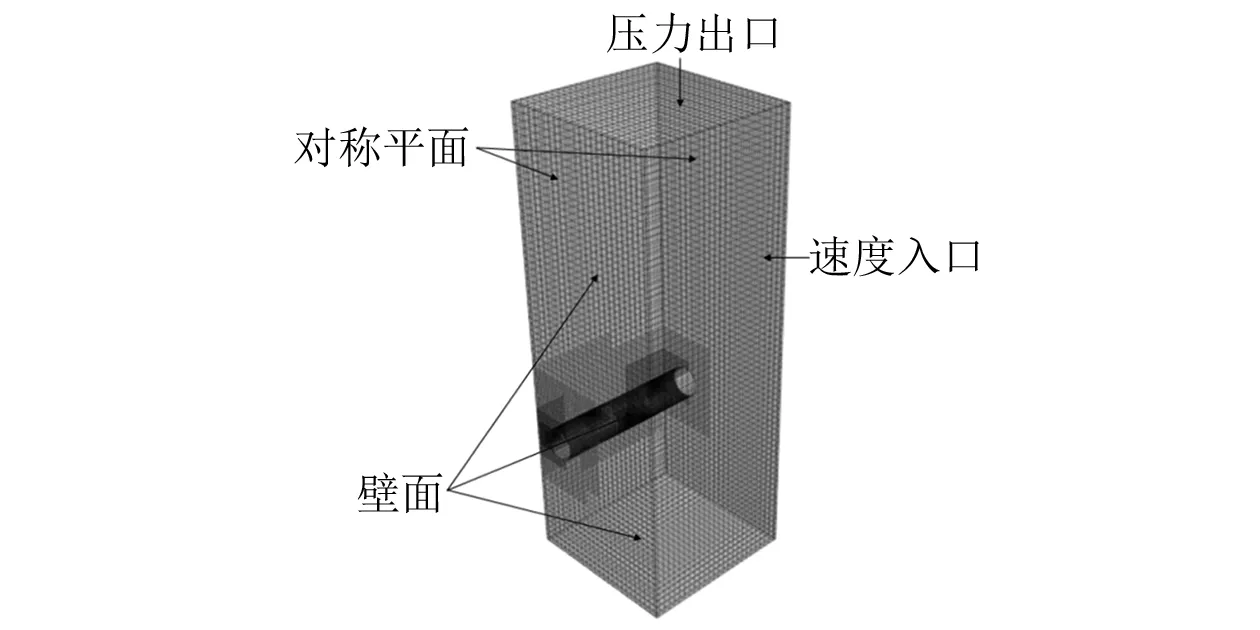
图4 计算域模型

此外，为了避免对称边界距喷孔过近发生边界反射，计算域在沿管长方向对称地各延长2倍孔间距，如图5所示，其中da为实际排气区域的距离。对于有n排喷孔的模型，da=50 mm(孔间距)×n。

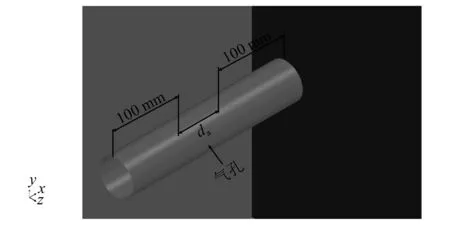
图5 孔计算域模型管长方向长度示例

物理模型选用三维隐式不定常湍流模型，考虑重力作用并启动单元质量校正。为了模拟气泡从气泡发生管产生及在水中的演变过程，采用欧拉多相分离流模型，设置水和空气两相，并给出相间相互作用尺度，其中相互作用尺度是指气泡幕中离散气泡的平均直径。气体和液体的材料属性如表3所示。

表3 气液材料属性

2.3 数值结果及分析

采用控制变量法研究气泡幕体积分数的变化规律，将可能对体积分数产生影响的因素罗列出来，包括喷孔数量、喷孔排列方式、孔径、通气量。这4个因素的可行域如表4所示。

表4 气泡幕体积分数影响因素及其可行域

此外，由于计算域的尺寸会随着所研究影响因素的改变而改变，如孔数增加，计算域的长度也会增大，因此计算时应将计算域换算成有效体积：

Ve=wdh

(8)

式中：Ve为计算域的有效体积；d为有效长度；w和h分别为计算域的宽度和高度，根据第2.2节，w=0.25 m，h=0.70 m。实际计算域体积V为

V=wLh

(9)

式中：L为计算域长度，其与孔数的关系为L=d+(4×50) mm。L的几何含义为在有效区域的基础上沿管长方向向两侧各扩充2倍孔距的距离，以防止产生壁面效应。

实际的气泡幕体积分数αe的计算式为

(10)

(1) 研究喷孔数量对气泡幕体积分数的影响。排列方式选用螺旋排列，孔径为2 mm，通气量为0.025 m3/min。计算得到不同喷孔数量下气泡幕体积分数的计算结果，如图6所示。由图6可知：随着喷孔数量的增加，气泡幕的有效体积分数稳定在3.76%，即气泡幕体积分数与喷孔数量的多少无关。

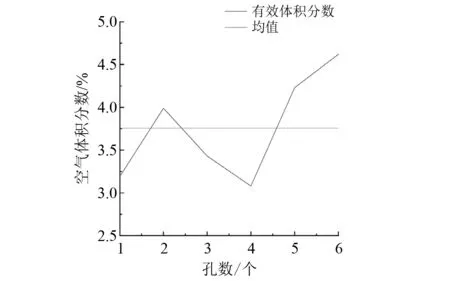
图6 气泡幕体积分数随喷孔数量变化

(2) 研究喷孔排列方式对气泡幕体积分数的影响。孔数设置为4孔(螺旋式的一个排列循环)，孔径为2 mm，通气量为0.025 m3/min。不同排列方式下气泡幕体积分数如图7所示。由图7可知，螺旋式排列方式的气泡幕体积分数较直列而言略有提高。

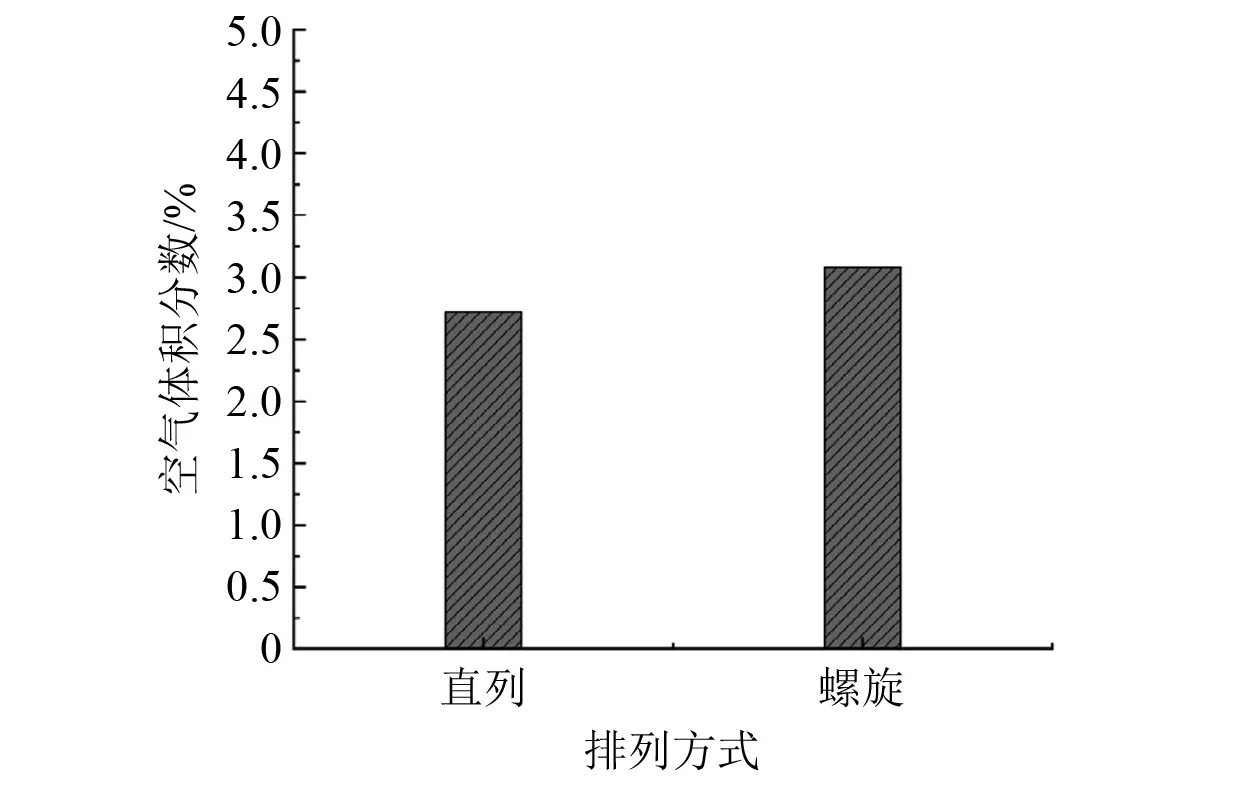
图7 不同排列方式下气泡幕体积分数柱状图

分析原因在于，直列布置时同一排孔在铅锤方向上共面，相邻孔之间的气泡幕会出现耦合现象，如图8所示。在气泡幕耦合作用下，相同体积下的气泡幕体积减小，使得体积分数减小。

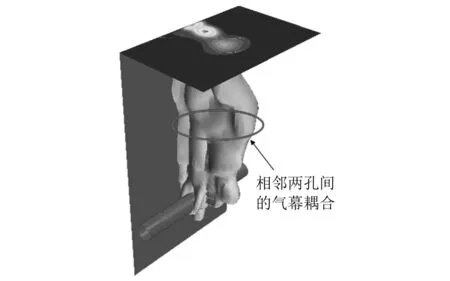
图8 直列排列下相邻孔间气泡幕耦合

(3) 研究不同孔径对气泡幕体积分数的影响。孔数设为4孔，排列方式选择螺旋排列，通气量为0.025 m3/min。计算结果如图9所示。由图9可知：随着孔径增大，气泡幕体积分数没有明显变化，基本稳定在2.98%。

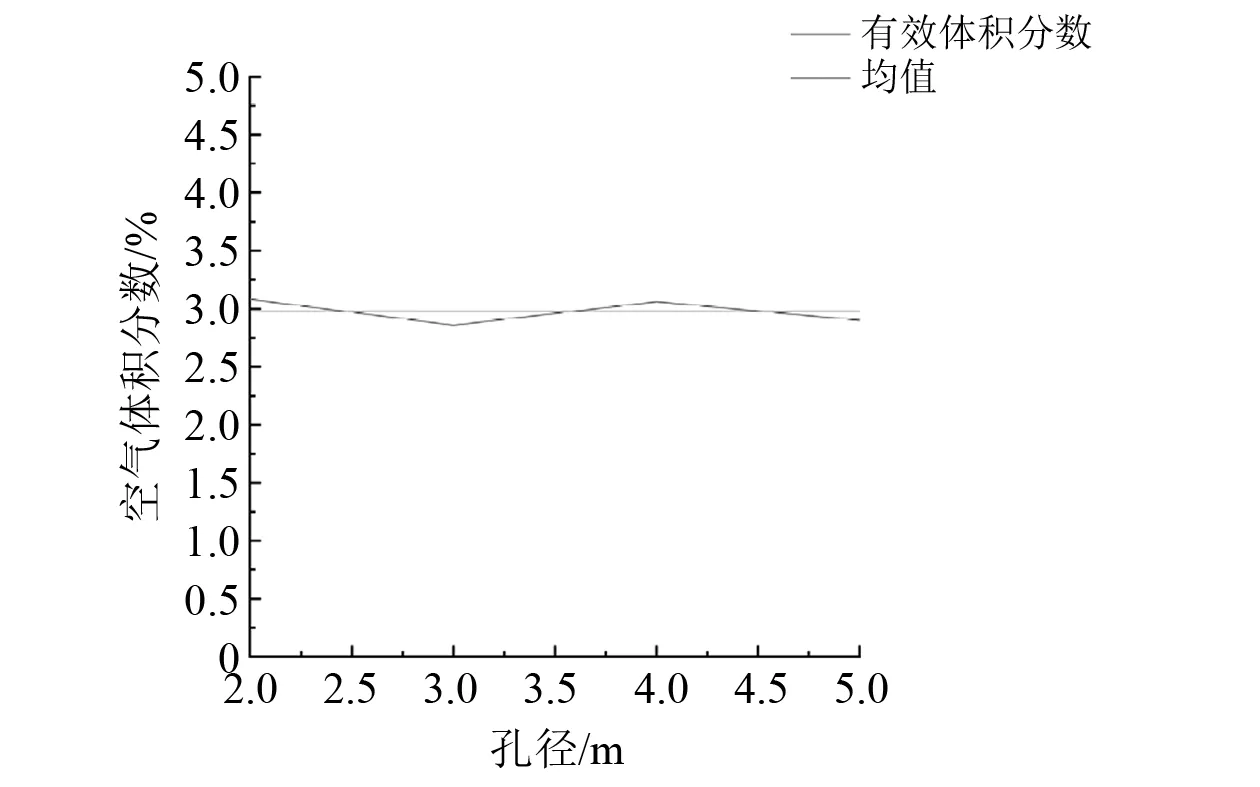
图9 气泡幕体积分数随孔径变化

(4) 研究通气量对气泡幕体积分数的影响。孔数设为4孔，排列方式为螺旋排列，孔径为2 mm。计算结果如图10所示。由图10可知，随着通气量增大，气泡幕体积分数也随之增加。

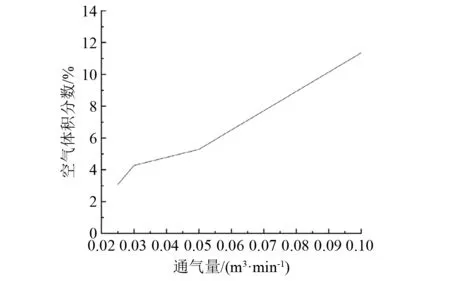
图10 气泡幕体积分数随通气量变化

3 结 论

(1) 针对螺旋排列模型，孔数和孔径对气泡幕有效体积分数的影响较小，原因是两孔间气泡幕的耦合作用较小，孔数增加，计算域体积增大，气泡幕量与体积之间近似为正比关系。

(2) 与直列排列相比，螺旋排列的气泡幕体积分数更大，原因是直列使同排相邻孔气泡幕间产生耦合作用，使得体积分数减小。

(3) 通气量对气泡幕体积分数影响较大，且为正相关，通气量越大，气泡幕有效体积分数越大。