基于SWAT的径流模拟参数优化方案及不确定性分析

陈 长 征，甘 容，杨 峰，左 其 亭

(1.郑州大学 水利科学与工程学院，河南 郑州 450001； 2.河南省地下水污染防治与修复重点实验室，河南 郑州 450001； 3.河南省出山店水库建设管理局，河南 信阳 464043)

0 引 言

水文模型是对水流运动过程及其逻辑机理的概化，随着计算机技术的高速发展，不同种类的水文模型陆续出现，逐步被应用到水旱灾害防治、水文预报、水资源管理、水环境保护和水文变化成因分析等领域[1]。

参数率定是水文模型优化的重要内容，但模型中通常涉及大量参数，难以同时保障全部参数的精确性，因此，评估参数敏感性、遴选关键参数对模型优化具有重要意义[2-3]。顺序不确定拟合算法(Sequential Uncertainty Fitting Version2，SUFI-2)是SWAT(Soil and Water Assessment Tool)模型率定的常用工具，刘伟等[4]比较了SUFI-2和广义似然不确定性估计算法GLUE(Generalized Likelihood Uncertainty Estimation)在参数率定和不确定性评估等方面的性能，结果表明SUFI-2算法的率定效率更高。周帅等[5]利用SUFI-2识别敏感参数及其置信区间，进而量化了参数交互作用不确定性对径流模拟的敏感性。Abbaspour等利用SUFI-2筛选出敏感参数后，通过超拉丁立方体抽样构造参数组合，将目标函数如纳什效率NS(Nash-Sutcliffe)的最优值对应参数组合的模拟结果选为最佳模拟，计算其决定系数R2(Coefficient of Determination)、百分比偏差PBIAS(Percentage Bias)、克林-古普塔效率KGE(Kling-Gupta Efficiency)等指标，依据各指标评估模拟性能[6]。应用SUFI-2的研究中，多数将NS作为目标函数确立最佳模拟[7-8]，但是除NS外的评价指标取值不确定性大，会出现NS评价的模型性能优秀，其他指标评价的性能差的现象，需要反复调参才能避免，降低了模型优化速率。

本文以淮河出山店水库为例，基于SWAT-CUP软件下广泛应用的SUFI-2算法，设置NS、R2和PBIAS3种目标函数，比较不同目标函数下的参数敏感性；结合模型性能评价准则，确立模型最佳模拟参数，建立了适用于该水库流域的分布式SWAT模型，可为流域未来水资源形势的科学把握和水库的合理调度提供基础支撑。

1 材料与方法

1.1 研究区概况

出山店水库是淮河防洪系统的骨干工程，总库容12.51亿m3，控制流域面积约2 900 km2，于2019年投入使用，是淮河干流上首个控制性工程。水库以上的淮河干流长110 km，近几十年流域内下垫面变化较小，总体上人类活动对河道径流影响较低，对水文数值模拟研究有利。流域内水系发育，支流众多，南侧支流坡陡水急，北侧支流弯多水浅；气候为亚热和暖温过渡带季风气候，多年平均气温15.1 ℃。多年平均降水量1 130.9 mm，汛期集中在6～9月份，时空分布不均，水旱灾害频生。研究区水文气象站位置如图1所示，其中大坡岭水文站控制面积1 640 km2，其来水信息对出山店水库的水情预报及洪水调度起着非常重要的作用。

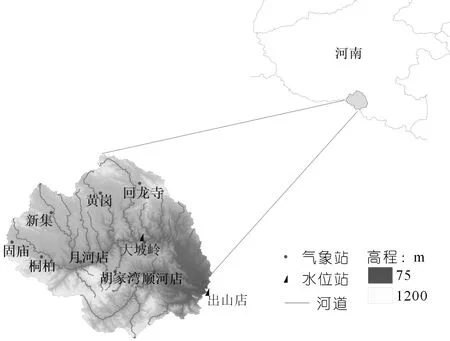
图1 研究区概况Fig.1 Overview of the study basin

1.2 数据介绍

模型构建需要的基础空间数据包括：数字高程模型DEM(Digital Elevation Model)、土地利用(见图2)和土壤类型(见图3)。土地利用采用的是资源环境科学与数据中心发布的《2010年中国土地利用现状遥感监测数据》。由DEM可知：研究区西北平均高程700～1 200 m，地势较高，山峦众多，中东平均高程100～300 m，地势平起伏小。由土地利用数据可知：耕地和林地占研究区总面积比例超过90%，其中耕地多种植水稻和小麦，水稻田约占70%耕地。由土壤类型数据可知：研究区中东分布累积性红土和不饱和始成土，分别占26%和23%，西北分布石灰性粗骨土和饱和黏性土，约占14%和20%。空间数据来源及分辨率如表1所列。

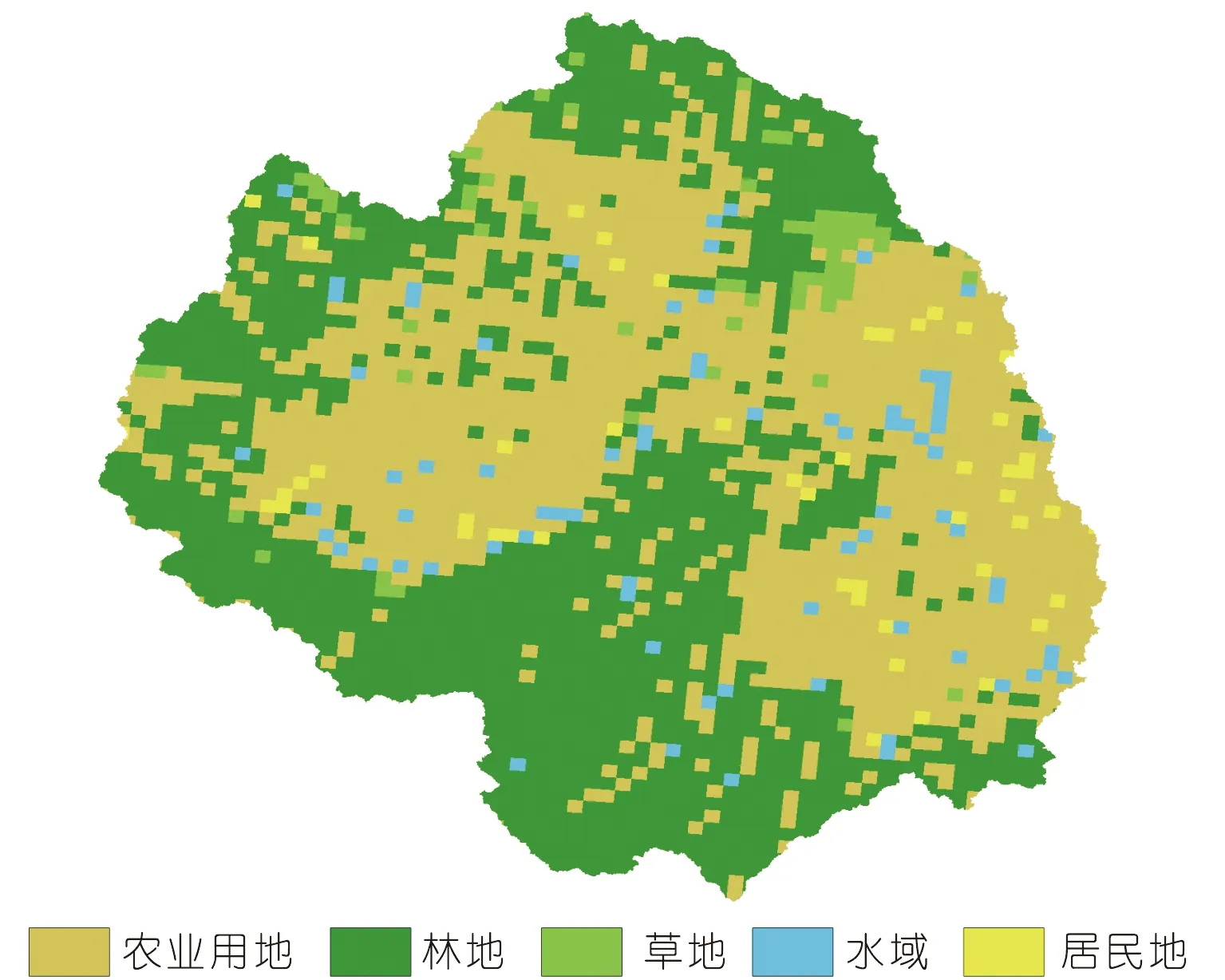
图2 土地利用类型(2010年)Fig.2 Type of land use (2010)

图3 土壤类型Fig.3 Type of soil

表1 空间数据介绍

气象数据源于中国气象数据网和地方水文年鉴，研究区境内气象站有桐柏国家站和8个地方站，时间序列为1958～2018年，包括逐日降水、最高气温、最低气温、风速、湿度和太阳辐射等；水文数据为水库上游大坡岭水文站1960～2018年逐月径流资料。

1.3 研究方法

研究包括3个主要部分：① 参数敏感性分析，② 参数范围优选和最佳模拟的确定，③ 模型验证，研究流程如图4所示。

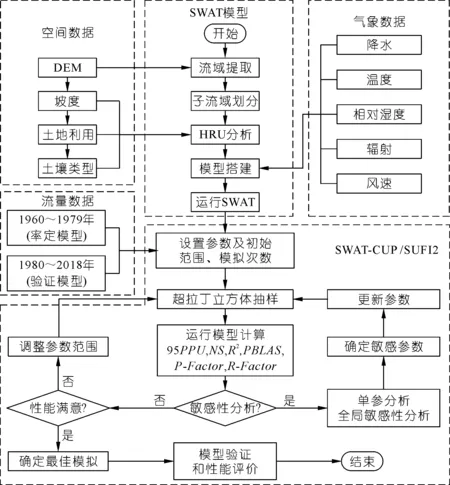
图4 研究流程Fig.4 Flow chart of the study

1.3.1SWAT模型和率定参数

SWAT是基于物理的分布式水文模型，它将流域划为多个子流域SUBs(Subbasins)，再依据土地利用、土壤和坡度特征将SUB划为水文响应单元HRUs(Hydrological Response Units)。模型中流域水文循环分为两个部分：第一部分为陆地阶段，控制进入河道的水、泥沙和营养物等；第二部分为河道演算阶段，计算水、泥沙等沿着河道运动至流域出口的过程。基于水量平衡方程计算陆地产流，如公式(1)，河网中的水经过主河道演算和水库演算，最终汇流至流域出口[9]。

(1)

式中：SWt为土壤最终含水量，mm；SW0为土壤前期含水量，mm；t为时间步长，d；Rd为第i天降水量，mm；Qsur为第i天地表径流量，mm；Ea为第i天蒸发量，mm；Ws为第i天土壤剖面底层的渗流和侧流量，mm；Qg为第i天地下水出流量，mm。

选用14种水文相关参数参与模型率定，如表2所列，其中数值空间分布具有异质性的参数(如CN2)，将其调参方式设为基于原始值进行缩放，目的是保留其空间分布特性，使流域建模的特征和实际更加贴近[10-12]。

表2 模型参数

1.3.2目标函数

目标函数是SUFI-2的关键输出，建立目标函数与模拟变量的联系可分析参数敏感性。选取纳什效率NS，确定系数R2和百分比偏差PBIAS作为本次模拟的目标函数，分别由公式(2)～(4) 表示。其中，NS可体现模拟径流和实测径流的总体贴合情况，但会赋予洪峰段更高的计算权重，容易忽视平水期或枯水期的拟合情况；R2是模拟值与实测值的拟合优度，弊端是R2对模拟值整体偏高或偏低的偏差响应不明显；百分比偏差PBIAS可体现模拟值和实测值的累积偏差，当模拟水文过程与实际趋势贴合情况良好时，PBIAS可更加精确地评估模型总水量平衡的效果[13]。

(2)

(3)

(4)

式中：Qm为实测流量；Qs为模拟流量；i和n为样本编号和总样本数量。

1.3.3参数敏感性分析

敏感性评估有助于识别关键参数，降低参数不确定性影响，进而提升模型优化效率，采用SUFI-2提供的一次性OAT (One-At-a-Time) 敏感性分析和全局敏感性分析方法评估参数敏感性。其中，OAT属于局部敏感性分析方法，做法是保持其他参数不变，调动单个参数，观察目标函数变化。OAT操作简单，可快速估计参数敏感程度；全局敏感性分析是目标函数在参数同时变化的情况下，对某个参数的平均变化率，方法如下[6]：

(1) 计算目标函数g(b)的雅可比行列式J：

(5)

(2) 通过Gauss-Newton法和克莱默定理估计参数下限的协方差矩阵C：

(6)

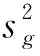
(3) 通过雅可比矩阵的中列平均值计算参数全局敏感度S：

(7)

1.3.4最佳模拟

基于95%置信水平上的不确定性区95PPU(95% prediction uncertainty)的评价准则，优选合适的参数范围。95PPU有两个特征指标：P-factor和R-factor。其中，P-factor是观测数据被95PPU包络的百分比，R-factor是95PPU的平均厚度，如式(8)和(9)所示。P-factor越大且R-factor越小，表明更窄的95PPU可包含更多的观测值，即95PPU不确定性越小。理论上P-factor=1且R-factor=0时，模拟值与实测值完全吻合，此时模型参数完全和真实流域一致。实际建模中认为P-factor>0.7且R-factor<1时，模拟的不确定性可接受[6]。

(8)

(9)

式中：n*为95PPU包含的观测样本个数，n为观测样本总数；Qu和Ql分别为模拟值累积分布的97.5%和2.5%分位点；σ为观测流量序列的标准差。

利用优选的参数最终范围模拟径流，计算全部模拟结果的目标函数，结合模型性能评价的分级准则(见表3)[14]，筛选出目标函数性能评价处于当前最高级的所有模拟结果；从这个范围中选取最佳模拟，便可避免使用单个目标函数确立最佳模拟的弊端。

表3 模型性能的评价准则

2 结果和讨论

2.1 参数敏感性分析

2.1.1OAT结果分析

模拟流域1960～1979年逐月径流过程，图5为OAT方法下NS，R2和PBIAS的变化特征，由图5可知：参数CN2、SOL_BD，SOL_AWC，CANMX，GWQMN，RCHRG_DP，ESCO和GW_REVAP改变时，目标函数的变化相对明显，参数的敏感性较强。其中，反映总体水量平衡的PBIAS对参数的变化反应最为灵敏，NS和R2对参数变化反应相对迟钝。

图5 调动单个参数时目标函数的变化特征Fig.5 Variation characteristics of the objective functions when changing single parameter

2.1.2全局敏感性分析

表4显示了基于不同目标函数计算的参数全局敏感度，其中T检验的统计值t-Stat(Statistical value of the T-test)是标准化后的取值，其绝对值越大代表参数越敏感；图6 为t-Stat的显著性检验结果，其中P-Value(Probability of rejecting the original assumption)是T检验拒绝原假设(参数不敏感)的概率，当P-Value≤0.05时，拒绝原假设即参数敏感。由图6知，参数CN2，CANMX，SOL_BD和GW_DELAY基于NS，R2，PBIAS计算的P-Value全小于0.05，即NS、R2、PBIAS都将其判定为敏感参数；基于R2判定为敏感的参数有CN2，CANMX，SOL_BD，GW_DELAY，ALPHA_BF和GWQMN；基于PBIAS判定为敏感的参数有CN2，CANMX，SOL_BD，GW_DELAY，GWQMN，GW_REVAP，ESCO，RCHRG_DP和SOL_AWC。

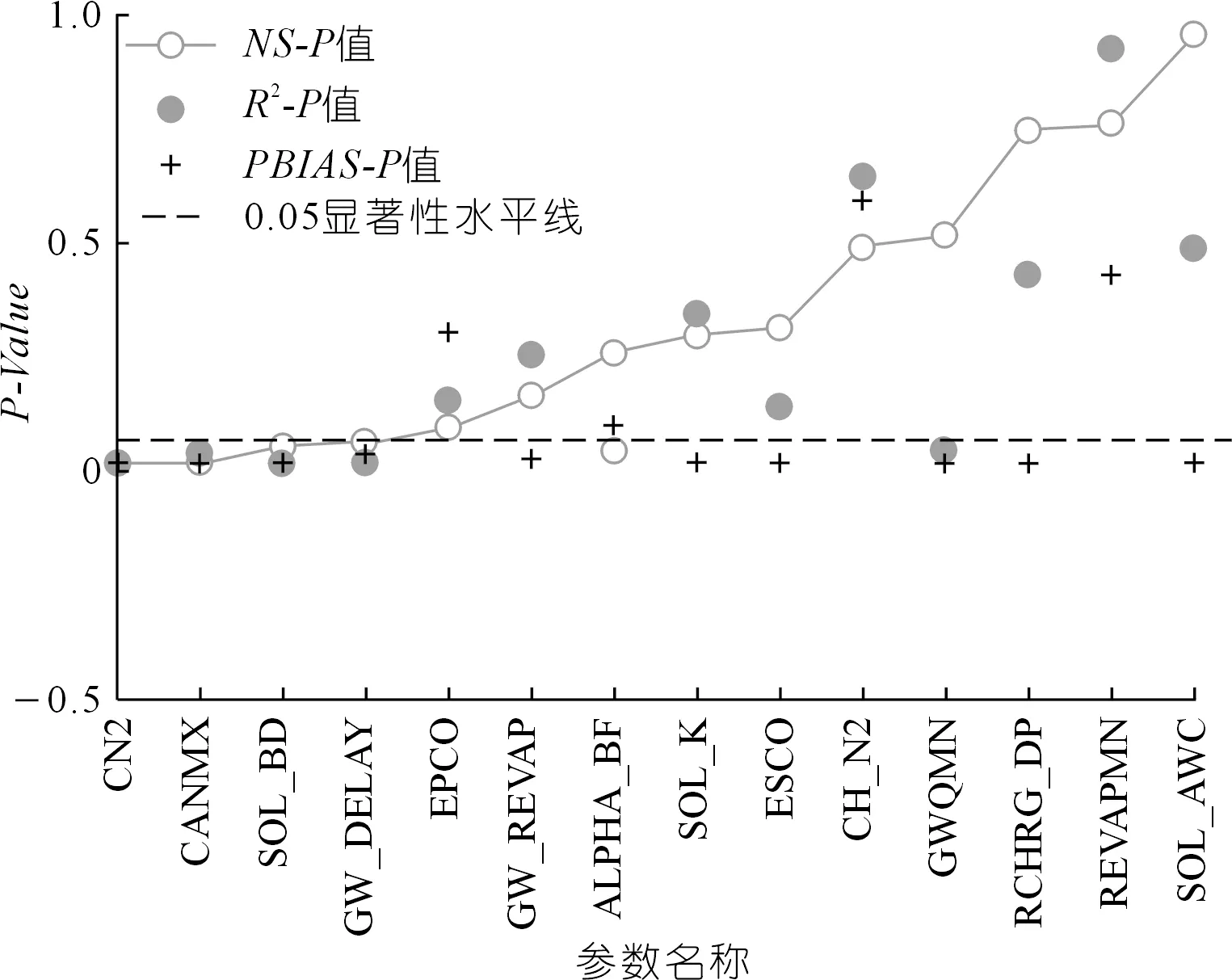
图6 全局敏感度显著性检验P-ValueFig.6 P-value of significance test for the global sensitivity

综上可发现：参数CN2，CANMX，SOL_BD和GW_DELAY的敏感性最强，是参数率定时需要被重点关注的对象；参数ALPHA_BF和GWQMN被R2判定为敏感，被NS判定为不敏感，表明ALPHA_BF和GWQMN对平水期和枯水期的水文过程影响更强；参数GW_REVAP，ESCO，RCHRG_DP和SOL_AWC只被PBIAS判定为敏感，原因可能是参数引起的丰枯水季流量偏差的作用相当，在径流总体走势上体现不明显。基于PBIAS计算的P-Value基本处于3个目标函数中的最低水平，基于R2和NS计算的P-Value互有高低，表明PBIAS对参数变化的响应度最强，与OAT结果一致。

全局敏感性分析确定了11个敏感参数，比OAT多3个，原因是OAT的前提是参数互相独立，而实际中参数敏感性会随其他参数改变而发生变化。因此，全局敏感性分析得出的参数敏感性结果更加可靠，但面对参数极多情况，OAT仍是初步掌握参数敏感度的实用方法，必要时可采用OAT迅速实现参数降维。

2.2 确定最佳模拟

采用PBIAS判断出的敏感参数参与模型率定，基于P-factor>0.7且R-factor<1的准则降低模拟不确定性，直到效果满意，参数最终范围如表4所列。图7是参数最终范围上500次随机模拟结果的目标函数的空间散点分布和坐标面投影。其中，NS-R2相关系数为0.67，NS-PBIAS相关系数为0.52，R2-PBIAS相关系数为0.07。这表明利用3个目标函数评价模型性能时，NS的综合能力最强，兼具了R2和PBIAS的部分特性。由图7可发现NS即将取到最优值时，R2和PBIAS的取值范围较大，NS最优值对应的PBIAS取值在优秀等级范围外。PBIAS评价的模型性能包括优秀、良好、一般和较差4个等级，NS评价的模型性能包括优秀和良好2个等级，R2评价的模型性能只有优秀等级，表明PBIAS确实对参数变化响应最灵敏，变化幅度最大。综上，采用限制评定等级的方法遴选最佳模拟，首先，限定NS，R2，PBIAS都处于优秀等级范围内，然后采用性能评价综合能力最高的NS作为寻优标准，以其最高值对应模拟为最佳模拟。

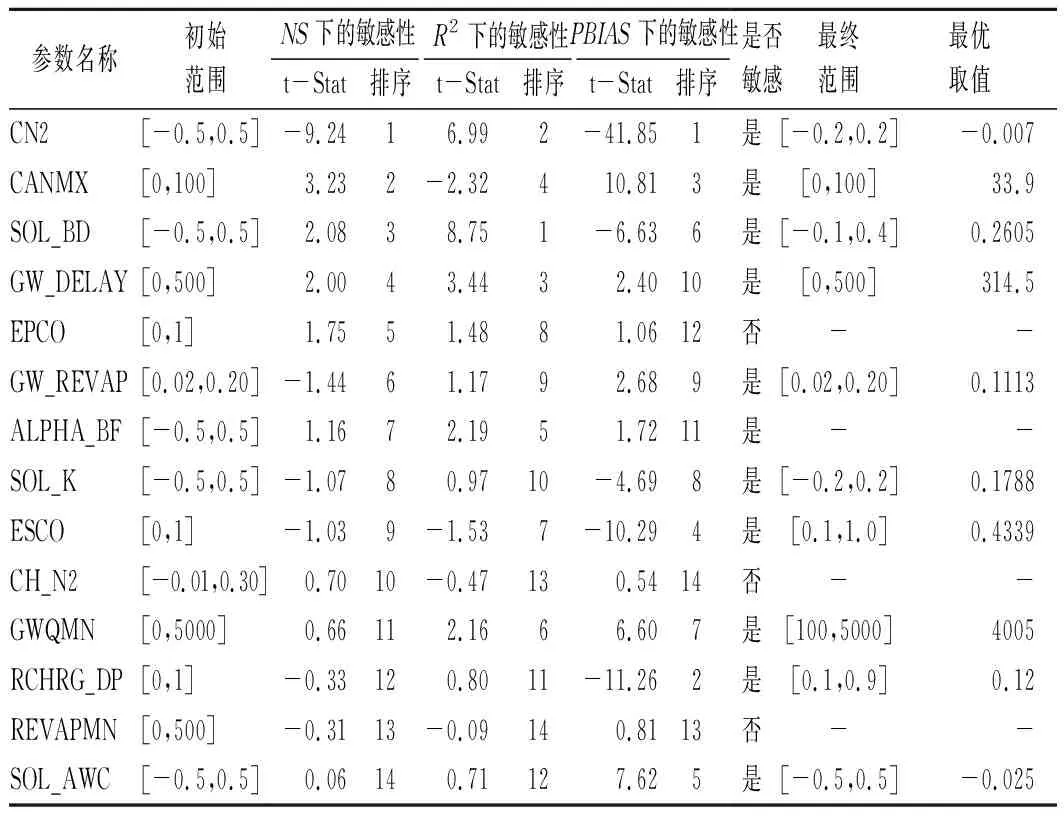
表4 参数在NS、R2、PBIAS为目标函数时的全局敏感性统计

2.3 模型应用

将最终参数范围和最佳模拟应用到流域1980～2018年的逐月径流模拟，分1980～1999年和2000～2018年两个验证期，评估最佳参数范围和最佳模拟的性能。

由率定期和验证期的降水分布可知(见图8)，率定期的逐月降水高于验证期01和02；由大坡岭水文站模拟逐月径流过程可知(见图9)：率定期和验证期01和02的P-factor分别为0.86，0.84，0.86，均大于0.7；R-factor分别为0.65，0.77，0.78，均小于1.0。表明模型输出的不确定性较小，可接受。率定期、验证期01和02的P-factor基本一致，表明率定出的参数范围在率定期和验证期01和02捕捉流域特征的能力相当；率定期的R-factor明显小于两个验证期，可能是由降水分布差异导致的。降水愈多，降水对径流的影响越强，径流和降水的关系越密切，参数对SWAT的影响相对越低，SWAT模拟性能更加优秀[15-16]。率定期与验证期的参数范围相同，但率定期降水较多，其输出的95PPU整体性能更优，表现为模拟径流过程向实测径流过程贴近，使95PPU的平均宽度更小。

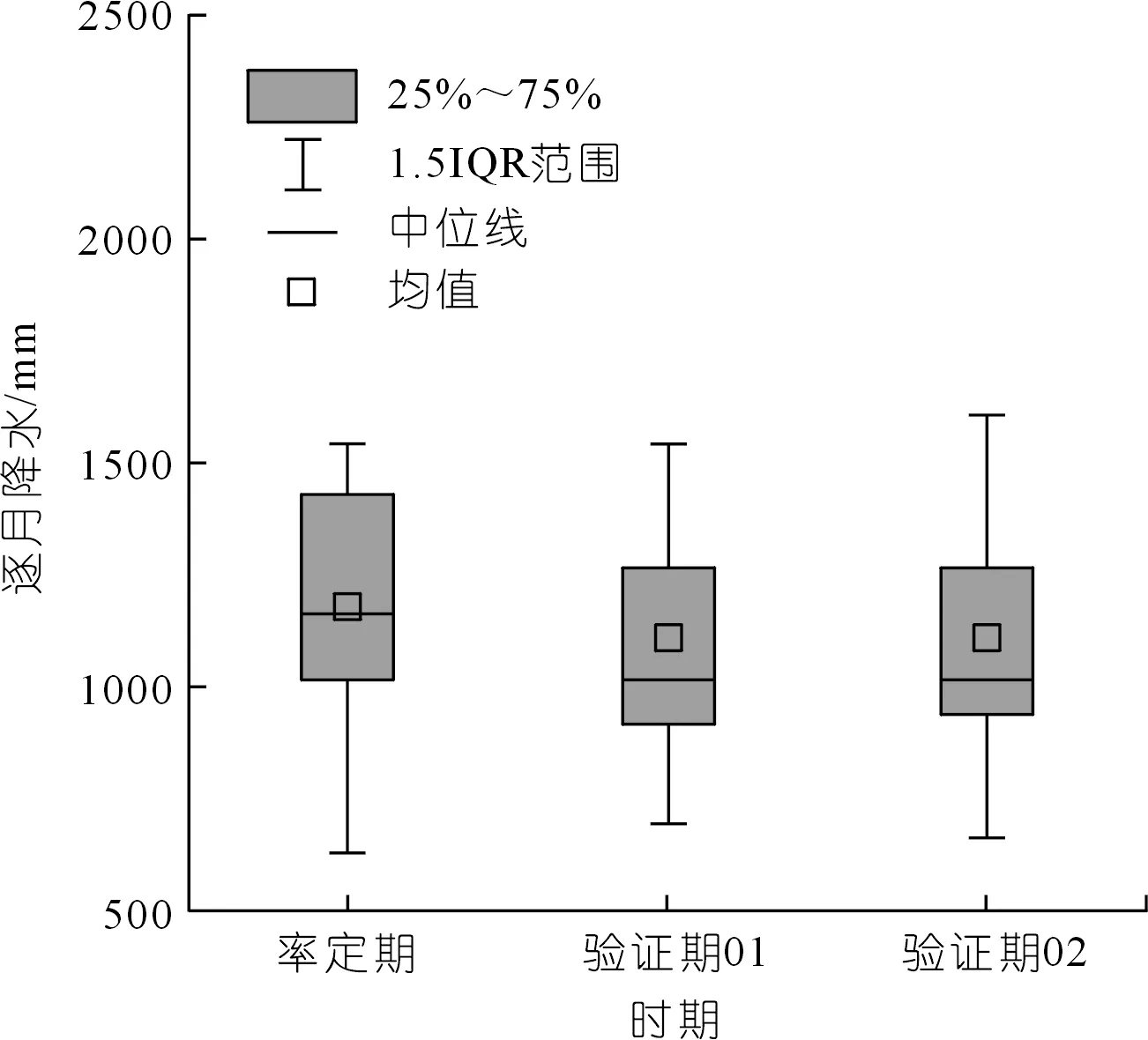
图8 逐月降水分布箱形图Fig.8 The box chart of monthly precipitation

图9 大坡岭站月径流模拟过程Fig.9 Monthly runoff simulation process of the Dapoling Hydrological Station

表5是最佳模拟在率定期、验证期01和验证期02的性能评价，由表可知不同目标函数的评价标准下，率定期和验证期的性能评价都为优秀，表明最佳模拟在长时间序列中可以取得稳定良好的性能，基于NS、R2和PBIAS3种目标函数的评价分级准则遴选最佳模拟的方法可行，这种方法可避免评价指标性能差别大时参数的反复迭代，在一定程度上提高了模型优化的效率。

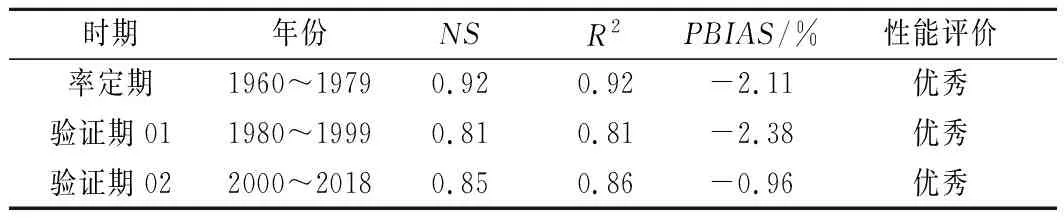
表5 不同时期最佳模拟的性能评价

3 结 论

本文基于设立NS，R2和PBIAS3个目标函数的SUFI-2算法确定了出山店水库流域的敏感水文参数，率定出参数最终范围和最佳模拟，结论如下：

(1) 基于不同的目标函数，确立的参数敏感性有所差异。NS，R2和PBIAS3种目标函数中，PBIAS对参数变化响应度最高，基于PBIAS确定的敏感参数最多，包括CN2，CANMX，SOL_BD，GW_DELAY，GWQMN， GW_REVAP，ESCO，RCHRG_DP和SOL_AWC；同类研究中，建议使用PBIAS作为目标函数筛选敏感参数，但当率定参数的数目较大时，建议使用NS作为目标函数，因为NS能够更快速地实现参数降维，牺牲部分模型性能提高优化效率。

(2) SWAT的径流模拟不确定性和降水分布相关，降水愈丰，降水对径流模拟的影响权重愈大，模拟的拟合效果越好；因此，固定参数范围后，率定期和验证期的P-factor变化不大，但降水越多，95PPU越向着性能更高的方向集中，使平均宽度R-factor变窄，从而表现为丰水期的模拟不确定性更小。

(3) 利用NS，R2和PBIAS评价参数最终范围内的全部模拟结果时，PBIAS评价的性能等级的不确定性最大，NS评价性能的综合能力最高。因此，建议通过限制PBIAS缩小选择范围，然后由高到低挑选NS的方法确定最佳模拟，可避免反复调参，提高效率。

(4) 出山店水库正处于试运行阶段，本文的研究结果对于水库流域开展水资源评价具有重要意义，特别是对流域未来气候下水资源变化形势的分析工作有一定参考价值。