PSO的航空发动机min-max控制器参数优化设计

朱日兴， 吴国洪

(1.南昌理工学院航天航空学院，南昌 330000； 2.南昌市小型通航飞机维修工程技术研究中心，南昌 330000)

0 引言

为了在不同推力水平之间进行良好的过渡且防止航空发动机在运行期间超出任何安全或操作限制[1-2]，航空发动机一般采用min-max燃油流量选择控制逻辑[3-4]，这种选择逻辑架构在实际中也得到了广泛应用，如通用电气GE90[5]和普惠2000[6]等航空发动机就采用该控制技术，然而，这种控制策略的非线性以及切换特性导致其控制器增益的参数整定过程十分复杂。目前，国内外学者对航空发动机min-max燃油选择控制器增益整定进行了相关研究：文献[7]采用了根轨迹分析法和时域分析法来设计控制器参数，但设计过程极具复杂性且不具有最优性；文献[8]采用迭代反馈调谐的方法来优化航空发动机加速度控制器的增益，但此方法容易陷入局部最优解，而且最终迭代次数需要进行相互比较来确定，优化过程比较复杂；文献[9-10]采用试凑法，虽然该方法简单且操作方便，但设计过程时间较长，且不具有全局最优性。

考虑到这种控制策略的非线性和切换特性，基于试凑法可能不会使发动机性能最优化，而基于梯度的优化方法在增益调节方面的性能较弱且无法全局寻优。因此，本文提出了一种基于非梯度优化技术-粒子群优化(PSO)算法的航空发动机min-max控制系统参数优化设计方法。优化目的是在尽可能短的时间内以最小的燃料消耗使航空发动机的输出变量满足所需的期望值，同时发动机中的关键变量不超过各自的安全范围。

1 基于PSO的min-max控制器参数整定

本章主要介绍粒子群算法在航空发动机控制系统的应用，其中min-max选择逻辑结构如图1所示。该发动机控制系统是由主控制与限制控制共同组成。限制控制中，限制器部分包括最大值限制器和最小值限制器。最大值限制器包括风扇转速限制、核心轴转速、加速计划和燃烧室压力；最小值限制器包括燃烧室压力和减速计划。粒子群优化算法是由KENNEDY和EBERHART研究发明的一种群体智能寻优算法，它是模拟自然界鸟类觅食行为而衍生出来的一种进化算法[11-14]。此算法调整参数少、简单易行、运行方便且收敛速度快，因而在许多领域得到了广泛的应用，已经成为当今智能优化方法领域研究的热点[15-17]。

min-max燃油选择控制器增益参数的整定过程被转化为一个数值优化问题。最终目标是在尽可能短的时间内以最小的燃料消耗使航空发动机的输出变量满足所需的期望值，同时各个关键的热力学变量不超过各自的安全范围。值得一提的是，发动机的燃油流量和相应的发动机推力与发动机的压力比(EPR)成正相关[18]。此外，由于本文考虑的环境条件为标准海平面，因此发动机的校正转速和发动机实际转速是相等的。

航空发动机控制系统的性能指标主要包括发动机过渡态响应时间和燃油消耗量[19]，因此目标函数可定义为

(1)

式中:wf为发动机过渡态期间的燃油消耗量；wf,max为发动机整个运行期间最大的燃油消耗量；T为仿真总时间；ΔT为采样时间；t为时间索引；首先对航空发动机性能指标进行归一化处理，然后根据权重系数α1，α2来决定每个变量的重要程度；tacc和tdec分别是发动机遵循飞行员油门指令所需的过渡态加速和减速时间。优化的主要对象是过渡态控制器和限制保护控制器的增益参数。控制变量由粒子群优化算法进行寻优调整，以最优化上述所设目标函数。

PSO算法和Simulink控制系统动态模型联合优化控制器增益参数的运算过程如图2所示，PSO算法不断改变min-max控制回路的增益参数，并迭代地模拟航空发动机性能，直到满足条件达到结果的最优化。

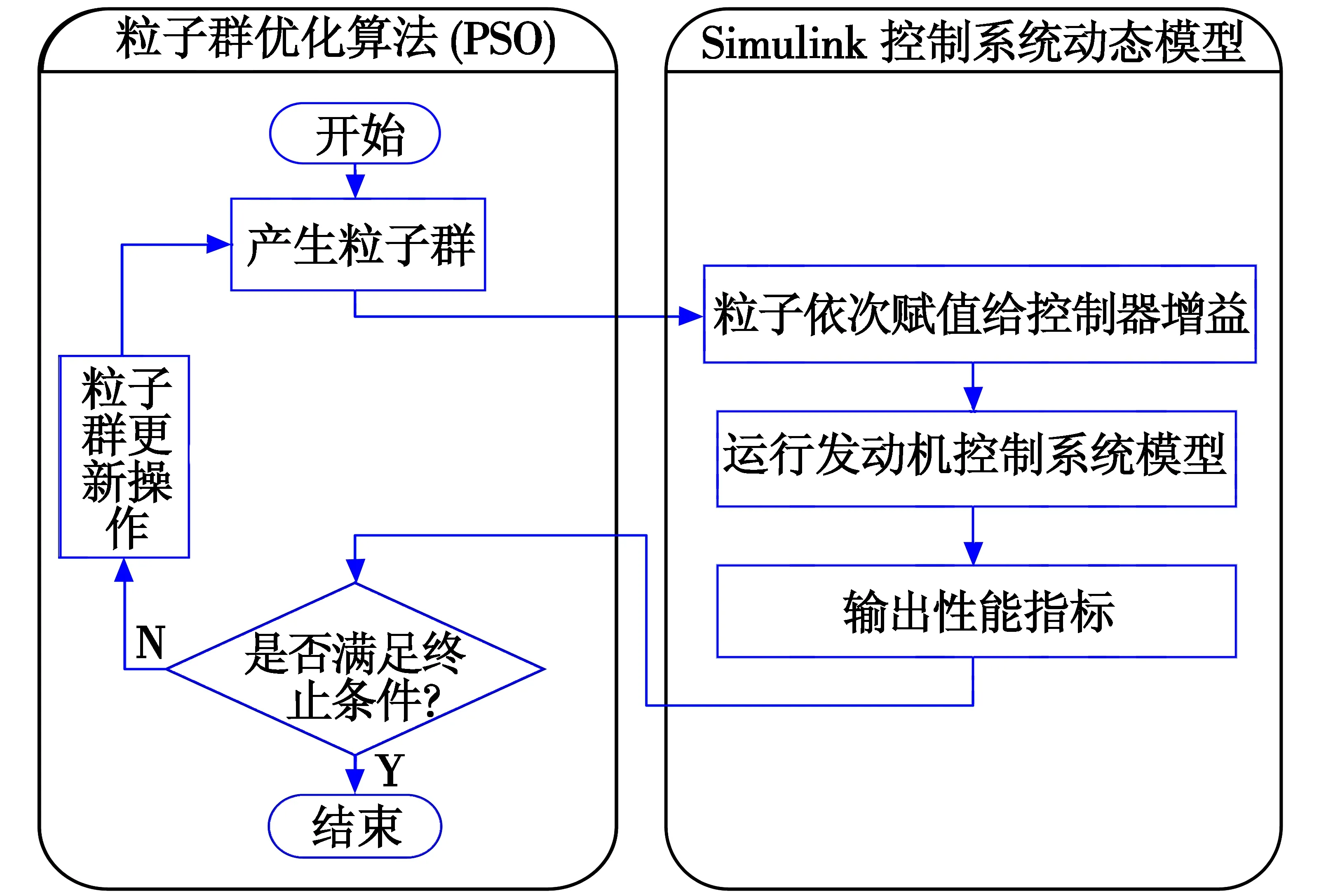
图2 基于PSO的优化过程Fig.2 Optimization process based on PSO

对于min-max控制系统中增益参数的优化，更新单体粒子的速度和位置从而找到最优解，即

xi=xi+vi

(2)

vi=w(t)×vi+α+β

(3)

(4)

(5)

w(t)=(wini-wend)(GK-g)/GK+wend

(6)

其中：惯性因子w(t)在PSO搜索过程中线性递减变化；初始惯性权值wini=0.9，最终惯性权值wend=0.4；最大迭代次数GK=150；粒子群总数为120；学习因子c1=c2=2。

图3为粒子群算法优化发动机排气温度(EGT)限制保护控制器增益的适应度曲线，由图中可看出适应度函数逐代递减。

图3 适应度值变化曲线Fig.3 Curve of fitness value

此外，为了证明算法的收敛性，优化过程已经使用不同的初始化粒子群，并做了几次运算。仿真表明，采用相同的适应度值函数，其最终得到的结果是相同的，而基于梯度的优化算法需要逻辑上接近最终解的初始解，否则它们会陷入局部最小值。

基于上述优化算法，依次可得到每个限制控制器的增益参数最优解，如表1所示，其中，Kp表示比例控制增益，Ki表示积分控制增益。

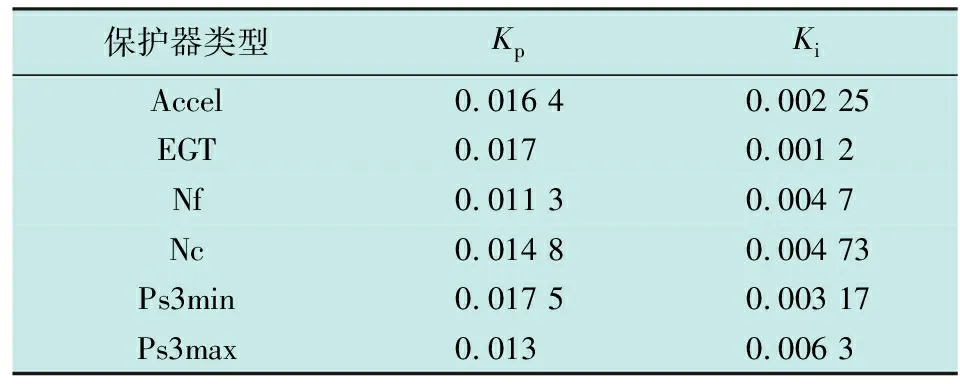
表1 优化后限制保护器的Kp和Ki值

图4和图5分别为优化前后的航空发动机控制系统性能指标仿真结果对比图。图中，wf表示燃油流量，1 lb≈0.453 6 kg。

图4 优化前后的响应时间对比图Fig.4 Comparison of response time before and after optimization

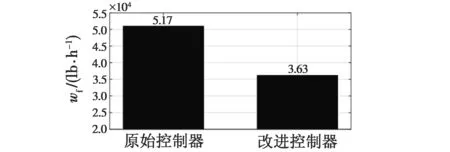
图5 优化前后的燃油消耗量对比图Fig.5 Comparison of fuel consumption before and after optimization

从图4和图5中可看出,经过PSO算法优化限制保护控制器增益参数后，发动机过渡态响应时间从6.31 s缩短到了3.8 s，响应时间缩短了约39%；燃油消耗量减少了30%左右。

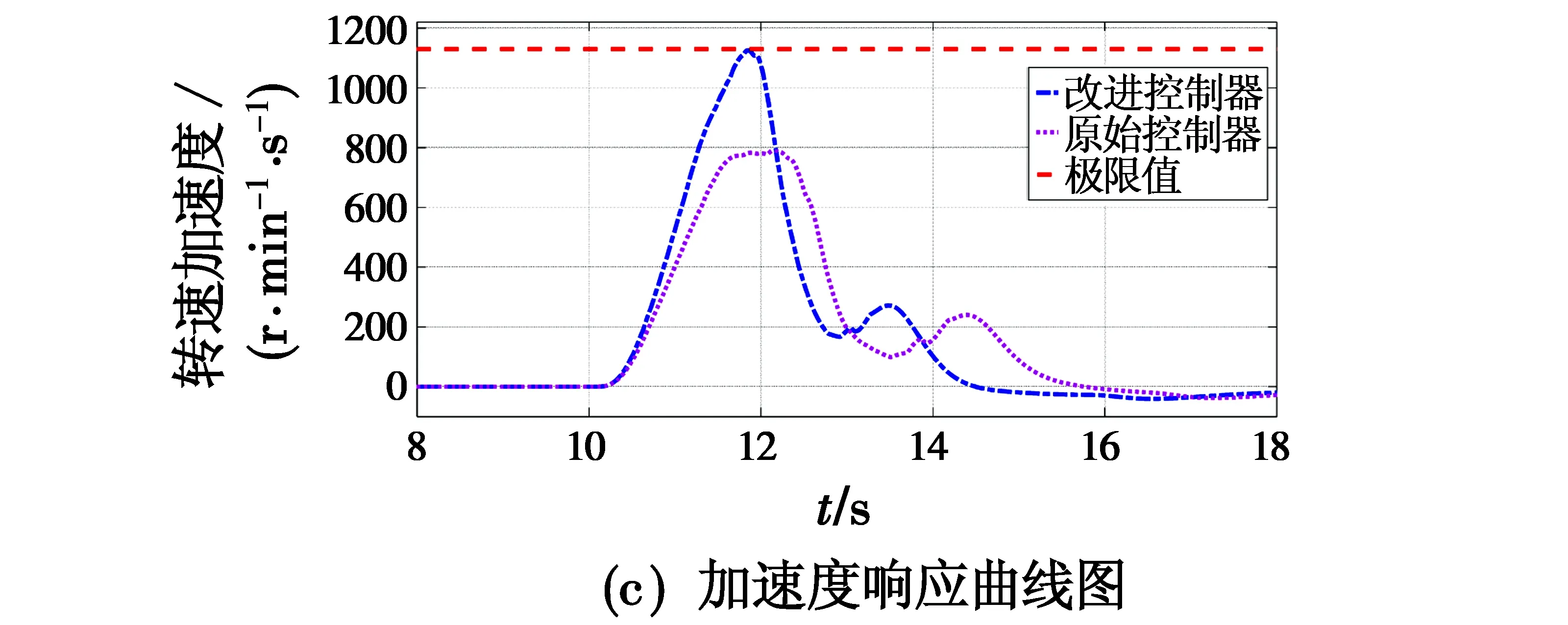
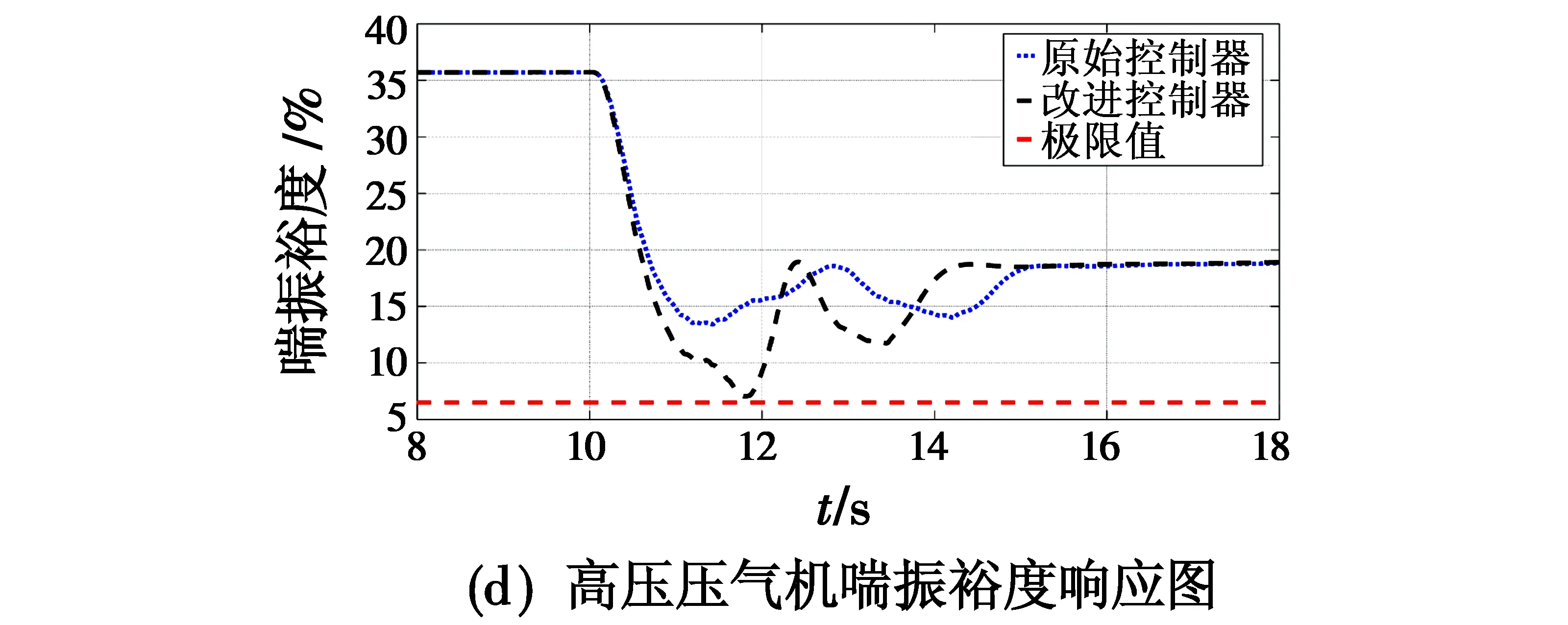
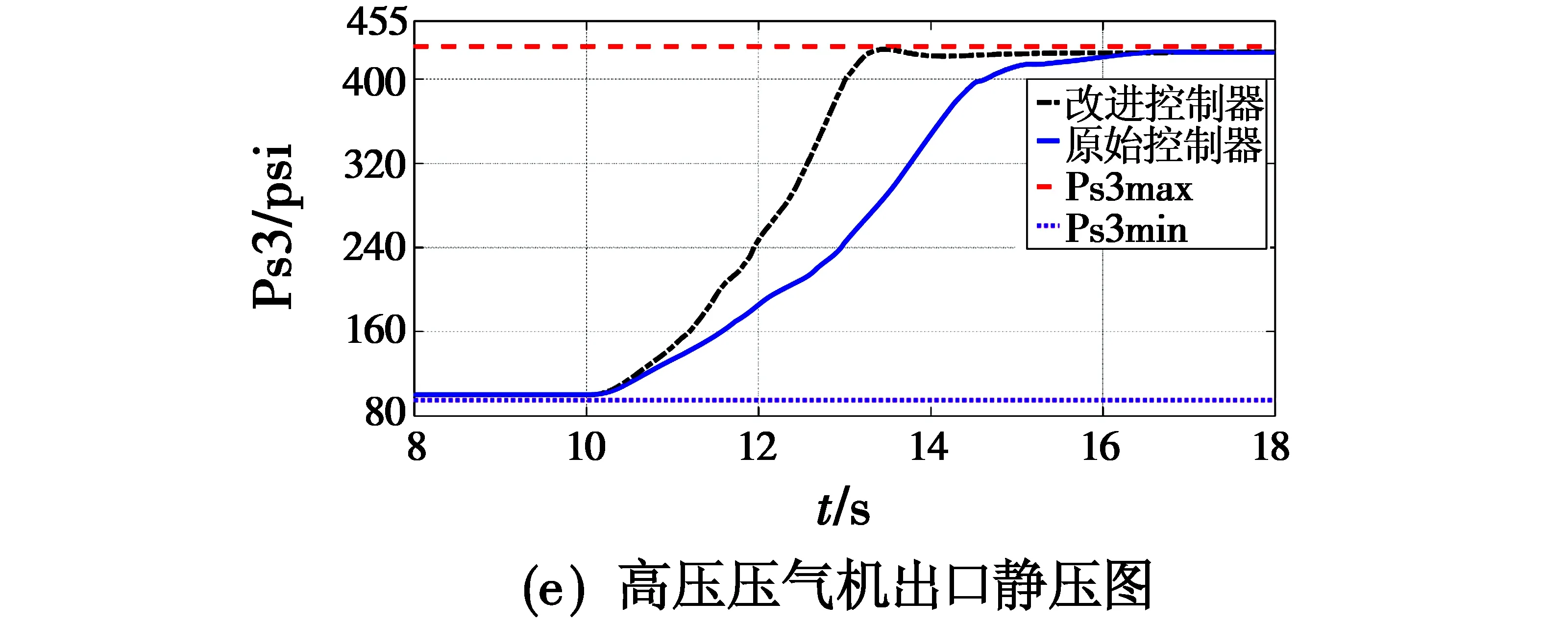
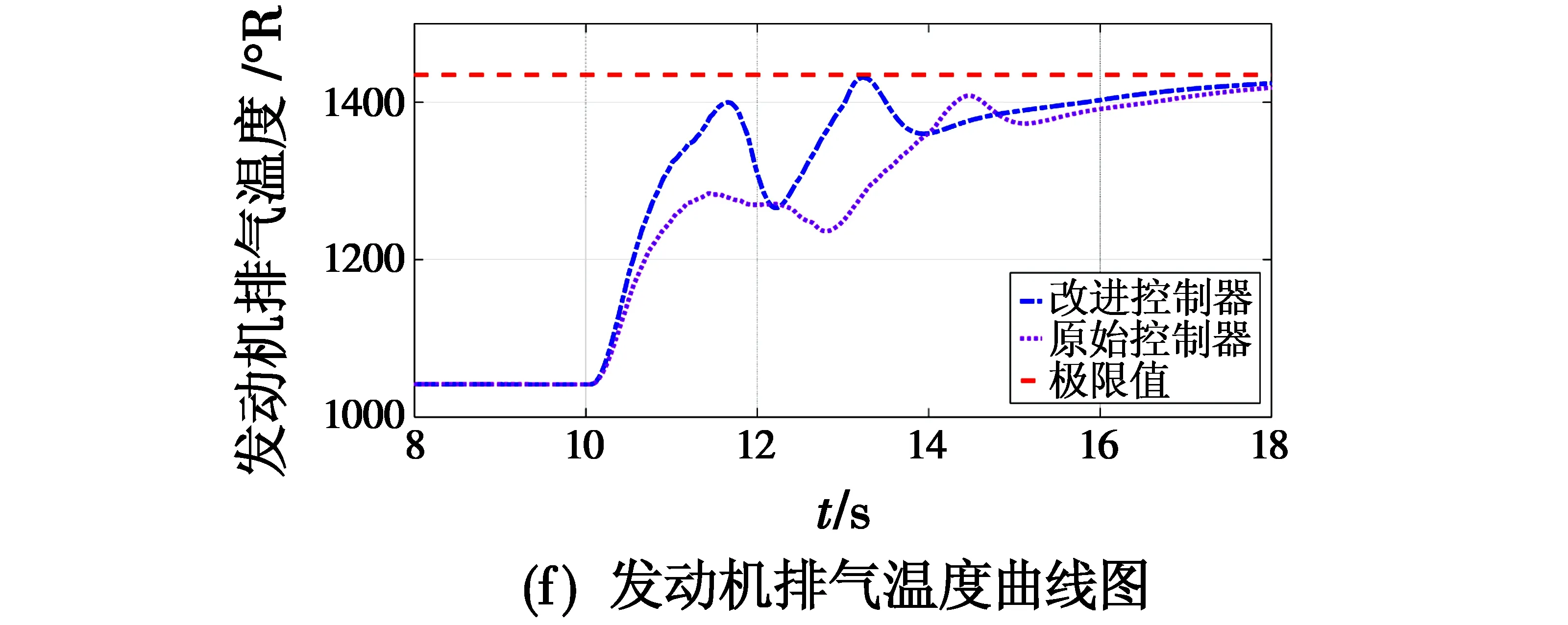
图6 优化后发动机热力学参数响应图Fig.6 Response of engine thermodynamic parameters after optimization

2 加权系数对发动机性能的影响分析

本章主要研究适应度函数中的加权因子对发动机性能指标的影响。其中,加权系数的选择主要取决于飞机的特殊用途以及过渡态性能要求。例如，对于军用飞机而言，发动机的加减速性能会显得更加重要；而对于民航客机而言，燃油消耗量的大小则显得更为重要[20]。

图7所示为适应度函数中加权因子的变化对目标函数中燃油消耗量和加减速时间最优值的影响。

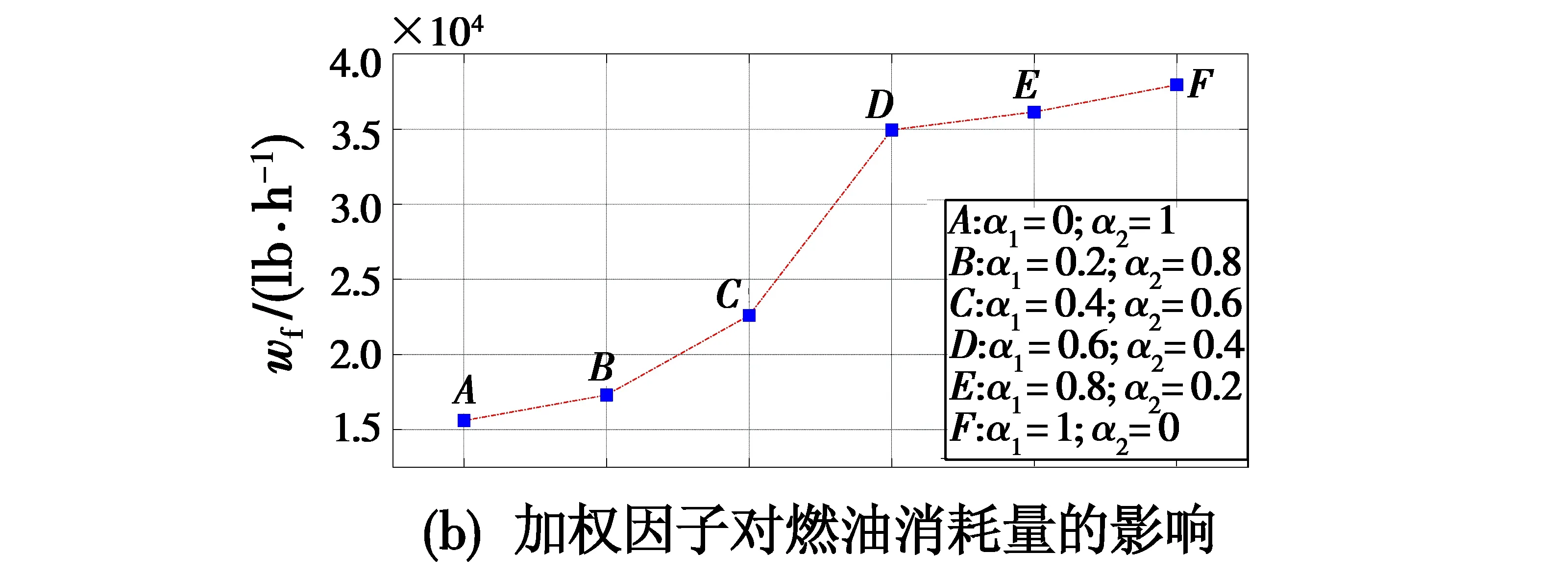
图7 加权因子对响应时间和燃油消耗量的影响Fig.7 Influence of weighting factors on response time and fuel consumption

由图7可看出，随着燃油消耗量加权因子α2相对于加减速时间加权因子α1的增大，在优化过程中耗油量逐渐减少，发动机加减速性能逐渐变差。而随着加减速时间加权因子α1逐渐大于燃油消耗量加权因子α2，航空发动机的过渡态性能有所提升，但耗油量也大幅度增加。以上仿真结果再次证明了本文所提出的智能优化方法在航空发动机min-max控制结构中参数优化的有效性及优越性。

图8为航空发动机过渡态响应时间和燃油消耗量之间相互均衡关系图。由图中折线变化趋势可知，飞机发动机过渡态性能的提高都是以牺牲燃油消耗量为代价的。

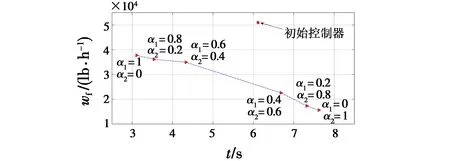
图8 加权因子对发动机性能的影响

3 结论

本文提出了一种基于粒子群优化算法的航空发动机min-max控制器增益参数优化设计方法。min-max燃油选择控制器增益参数整定被转化为最优化问题，优化的主要对象是过渡态控制器和限制保护器的增益参数。目的是在尽可能短的时间内以最小的燃料消耗使航空发动机的输出变量满足所需的期望点，同时发动机中的关键变量不超过各自的安全范围。在该数值优化问题中，适应度函数被设计为加权发动机响应时间和加权燃油消耗量的总和，并在航空发动机控制系统仿真平台对此优化设计方法进行了数值仿真。

仿真结果显示，此方法不仅有效地改善了航空发动机过渡态的性能，而且能够保证发动机在系统给定的极限值范围内安全运行，证明了该方法的有效性及优越性。此外，进一步分析了目标函数中加权因子对发动机性能指标(控制系统响应时间和发动机燃油消耗量)的影响，并绘制了三者之间的平衡关系图，可为发动机设计所选择的权重因子提供参考依据。