雄安新区剪切波速剖面VS30 估算模型研究1

张 肖 张 合 云 萌 汪 飞

1）昆明理工大学, 昆明 650500

2）河北红山巨厚沉积与地震灾害国家野外科学观测研究站, 河北邢台 054000

3）雄安新区震灾预防中心, 河北雄安新区 071700

4）中土大地国际建筑设计有限公司, 石家庄 050000

引言

土层剪切波速是场地分类的重要参数，广泛应用于工程勘察、地震工程等领域。王笃国等（2021）提出，场地类别显著影响峰值加速度放大系数和特征周期，对工程场地抗震设防尤为重要。目前我国规范使用VS20和覆盖层厚度作为场地分类的主要参数，如《建筑抗震设计规范》（GB 50011-2010）（中华人民共和国住房和城乡建设部等，2010），而国外许多国家和地区采用VS30进行场地分类，如Federal Emergency Management Agency（2015）。这种差异的存在，使国内学者进行研究对比、应用国外研究成果时存在场地分类和参数不统一等问题，因此开展VS30研究具有一定意义。Boore 等（2011）认为受场地环境、预算约束、超出设置的速度阈值等因素制约，存在较多剪切波速剖面深度不足30 m 的情况。因此，准确估算VS30成为国内外学者研究方向。

目前国内外广泛采用的方法是对大量剪切波速数据进行拟合，从而计算VS30。许多专家提出VS30估算模型及其适用性研究（Cadet 等，2009；Dai 等，2013；Zhao 等，2013；Wang 等，2015；Hassani 等，2016；Xie 等，2016），Kuo 等（2011）提出利用速度模型底部速度值代替等效剪切波速值的常速度外推模型；Boore 等（2004，2011）根据美国加州、日本KiK-net 等钻孔数据提出速度梯度外推模型；Wang 等（2015）提出利用双深度模型方法估算VS30。国内学者基于以上常用模型提出了适合我国不同地区的VS30估算模型，并对常见模型适用性进行了研究（喻畑等，2015；刘培玄等，2015；胡进军等，2018；江志杰等，2018；党鹏飞等，2019；张龙飞等，2020）。

Boore 等（2011）提出，在土层性质类似的国家或地区，VS30与某深度的剪切波速间存在一定经验关系，基于美国加州钻孔剖面深度超过30 m 的台站钻孔数据，得到加州地区剪切波速剖面深度小于30 m 的VS30，并给出速度梯度模型。笔者通过雄安新区435 个钻孔剖面数据，采用Boore 等速度梯度模型进行计算对比，发现仅当钻孔剖面深度达21 m 以上时，基于Boore 等（2011）模型的VS30估算值和实测值相关系数可达0.9 以上，因此认为Boore 等（2011）模型参数不适用于雄安新区，需找到适合雄安新区的VS30经验估算模型。

1 钻孔数据

本文收集了雄安新区起步区区域性地震安全性评价工程中435 个钻孔（图1），雄安新区工程地质条件相对单一，收集的钻孔基本涵盖雄安新区全域工程地质情况（除白洋淀水域）。435 个钻孔中，最大深度为100 m，最小深度为80 m，其中深度80～89 m 钻孔共313 个，深度90～99 m 钻孔共120 个，深度100 m钻孔共2 个。按照Federal Emergency Management Agency（2015）场地分类标准，雄安新区435 个钻孔均位于D 类场地。本文从435 个钻孔中随机选取300 个钻孔进行回归分析，其余135 个钻孔进行VS30估算模型可靠性研究。

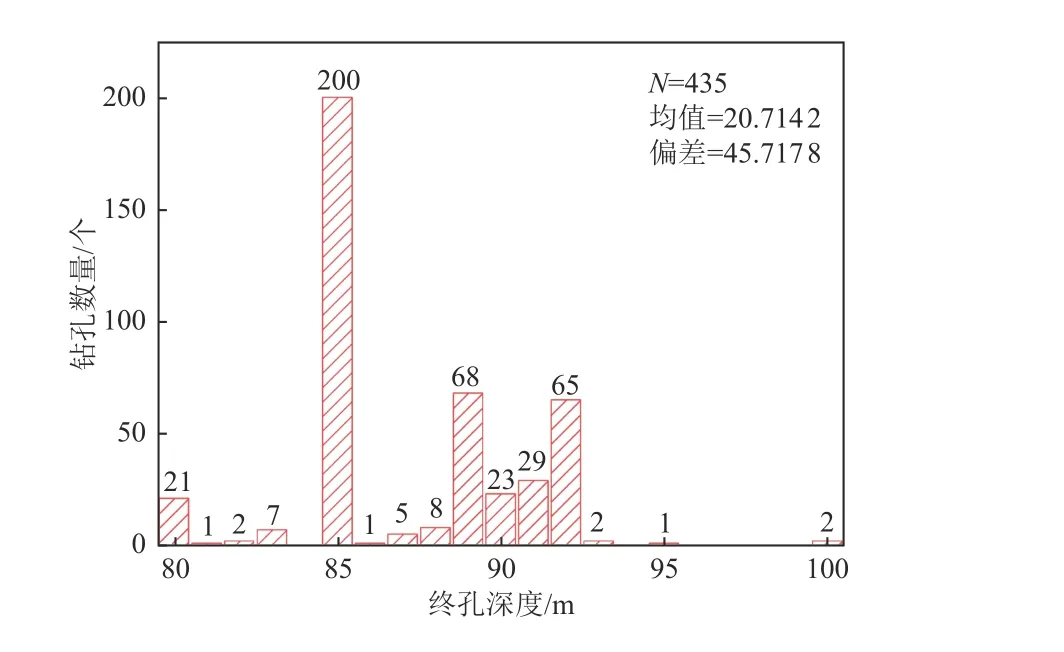
图1 不同深度钻孔数量分布Fig. 1 Number distribution of boreholes with different depth

2 VS30 模型拟合方法

为更好地进行数据拟合与模型对比分析，获得雄安新区近地表剪切波速剖面深度不足30 m 的VS30估算模型，本文在Boore 等（2011）模型的基础上，对对数二次模型和对数三次模型进行拟合分析，线性拟合公式为：

本文采用回归分析方法，利用SPSS 软件对雄安新区300 个剪切波速剖面深度达30 m 以上的场地数据进行处理，拟合出深度为5～29 m 时VS30和VSz（深度z＜30 m）经验关系，获得各类模型系数，如表1 所示，各类模型在不同深度处的拟合结果如图2 所示。

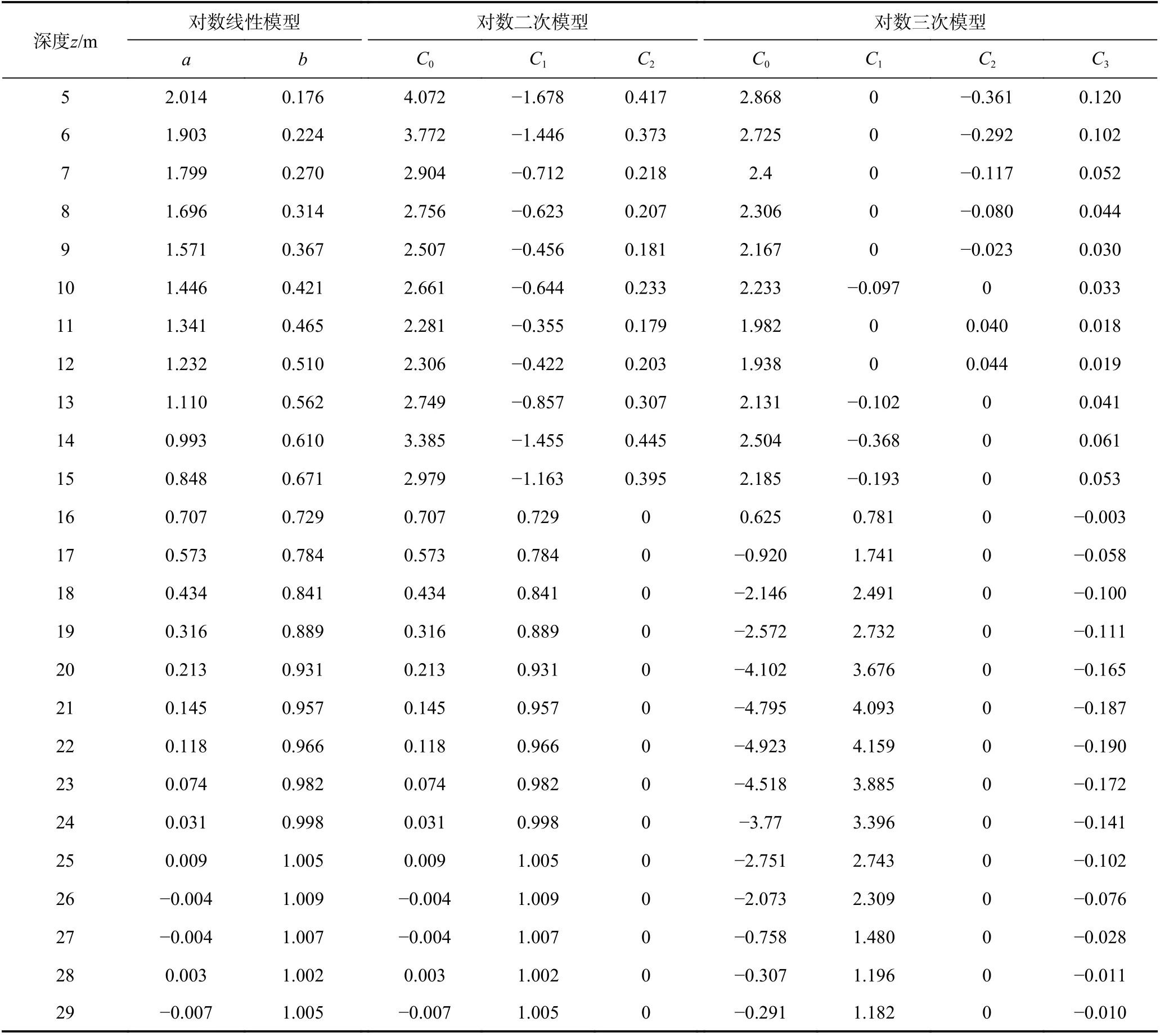
表1 雄安新区钻孔VS30 估算模型拟合系数Table 1 The fitting coefficients of VS30 estimation models of boreholes in Xiong’an

受雄安新区钻孔资料缺乏和环境、经济条件等因素限制，当剪切波速剖面深度不足30 m 时，可由表1参数进行雄安新区VS30估算及场地类别划分。由图2 可知，随着钻孔剖面深度的增加，对数线性模型、对数二次模型和对数三次模型拟合误差减小。

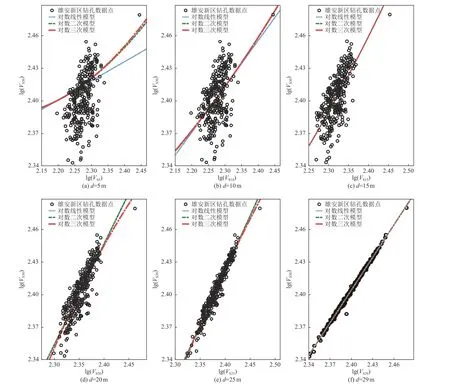
图2 不同深度处3 种模型拟合结果Fig. 2 Fitting results of three models at different depths

3 VS30 估算模型可靠性检验

3.1 估算模型可靠性

为得到适合雄安新区的估算模型，需将3 个估算模型得到的等效剪切波速VSE30与测量值VS30进行可靠性和相关性分析，皮尔森相关系数r及二者的残差标准差σRES可由下式计算：

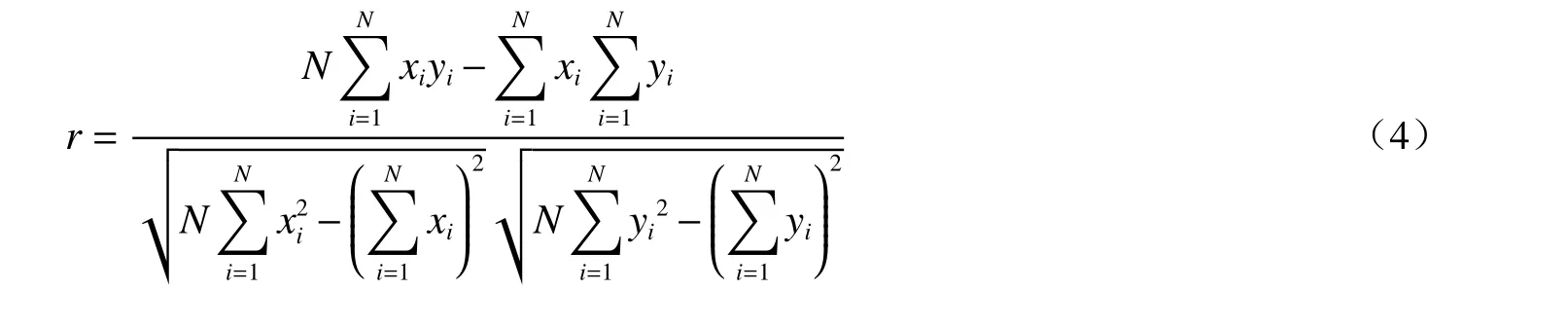
不同深度下对数线性模型、对数二次模型、对数三次模型与Boore 等（2011）模型的VSE30和VS30对比如图3 所示，模型计算的残差标准差如图4 所示。

由图3 可知，随着深度的增加，各模型得到的VSE30与VS30越接近；对数线性模型、对数二次模型和对数三次模型计算结果更集中，而Boore 等（2011）模型计算结果较离散。计算结果表明，对数线性模型、对数二次模型和对数三次模型得到的皮尔森相关系数均达0.99 以上，但对数三次模型残差标准差略小于对数线性模型和对数二次模型（图4）。当深度小于10 m 时，对数线性模型、对数二次模型和对数三次模型均存在约3%的低估现象，其中对数二次模型预测值相对更准确；当深度小于15 m 时，Boore 等（2011）模型存在严重低估VS30的情况，可能因为剪切波速对数关系具有区域性特征所致。

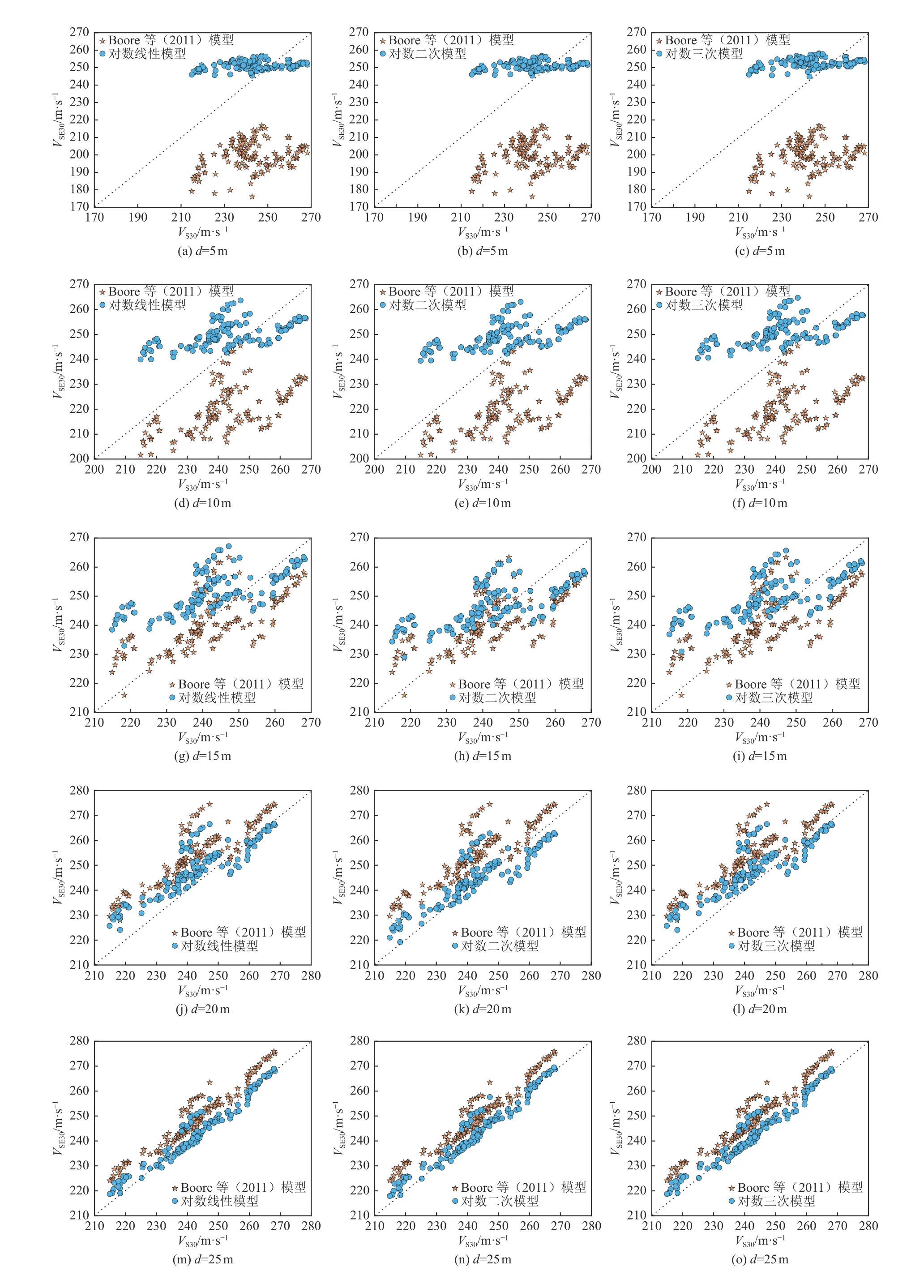
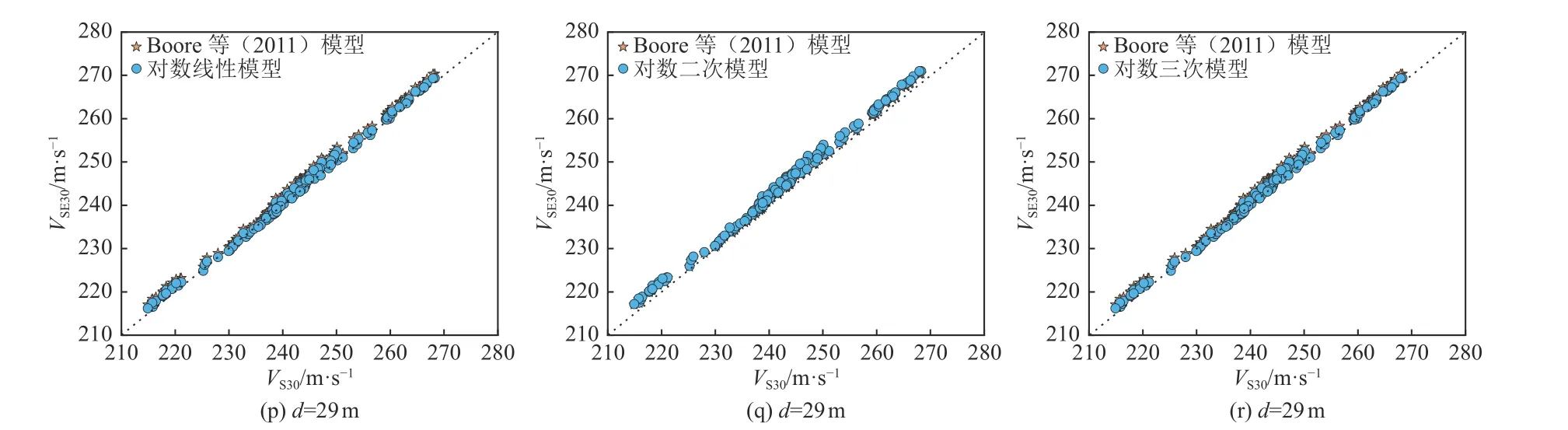
图3 不同深度下3 种模型与Boore 等（2011）模型VSE30 和VS30 对比Fig. 3 Comparison of VSE30 and VS30 between the three models and the Boore model at different depths

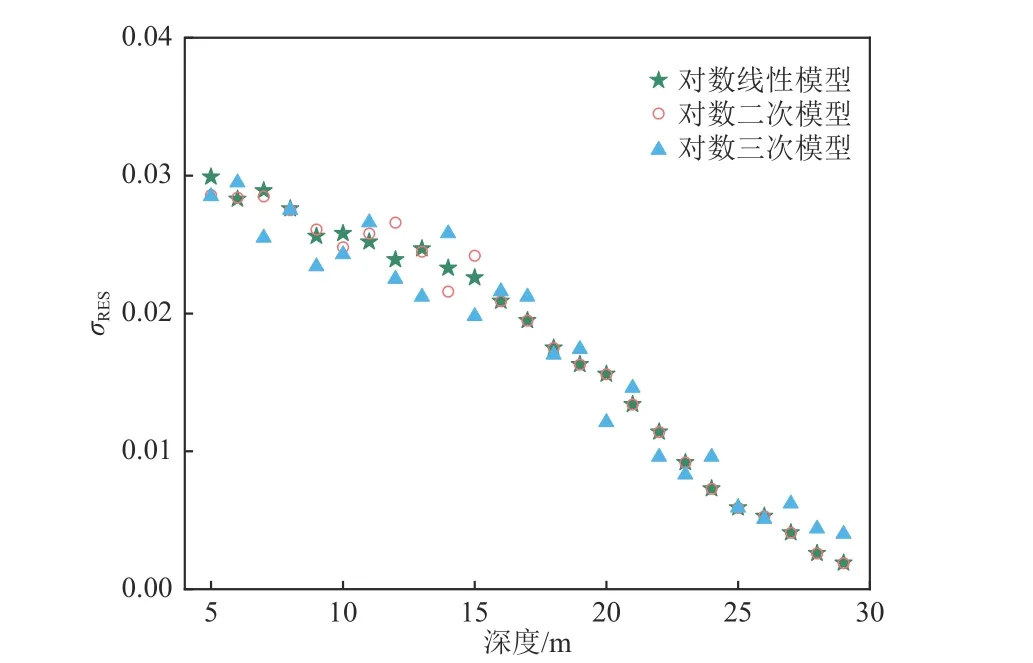
图4 不同深度下3 种模型残差标准差Fig. 4 The standard deviation of residuals of the three modles at different depths

3.2 估算模型适用性

Wang 等（2015）提出通过估算值VSE30和实测值VS30之间的相对误差Rerror研究模型适用性，计算公式为：

相对误差计算结果如表2、图5 所示。由表2 可知，对数线性模型相对误差为0～15.25%，对数二次模型相对误差为0～14.81%，对数三次模型相对误差为0.01%～14.79%，Boore 等（2011）模型相对误差较大，为0.16%～27.48%。由图5 可知，随着深度的增加，对数线性模型、对数二次模型和对数三次模型相对误差集中为0～5%，其中对数三次模型对应的钻孔数量略多。

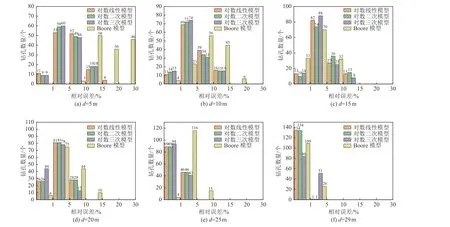
图5 各估算模型相对误差柱状图Fig. 5 Histogram of the relative error of VSE30 estimated by each model

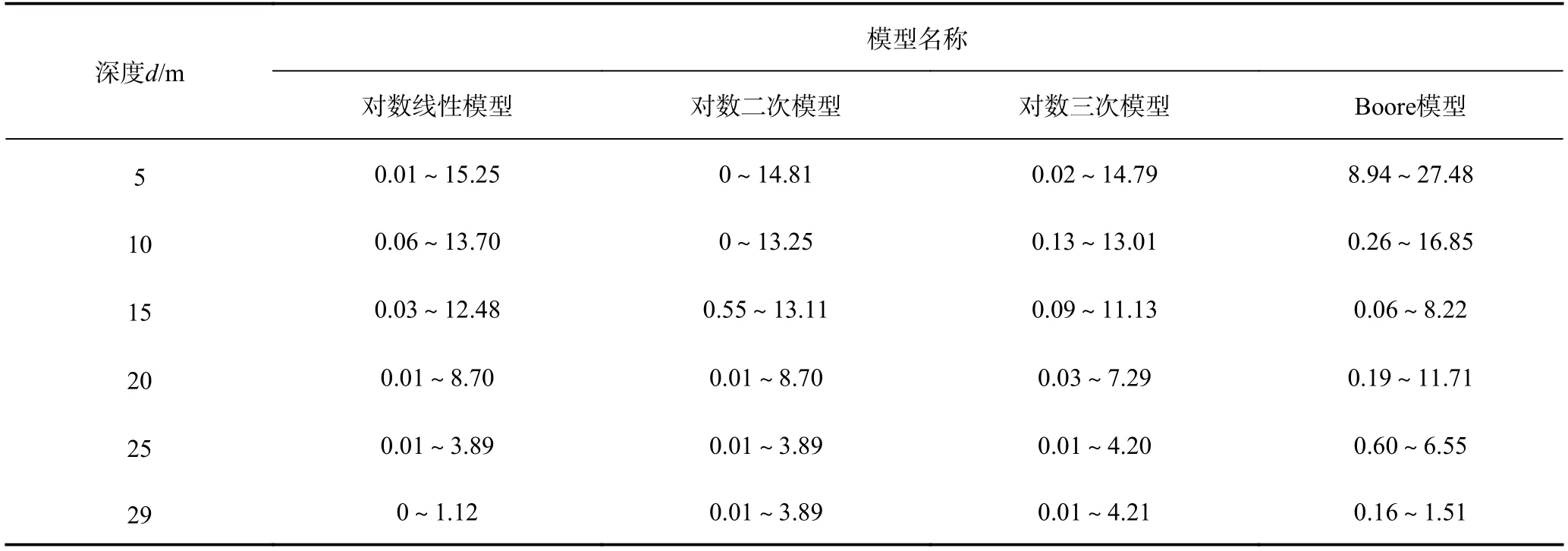
表2 各估算模型相对误差（单位：%）Table 2 Relative error range of each estimation model（Unit：%）

4 讨论与结论

本文基于雄安新区起步区区域性地震安全性评价工程435 个钻孔剖面数据，选取其中300 个钻孔剖面进行回归分析，利用剩余的135 个钻孔剖面数据进行模型可靠性检验,得到以下结论：

（1）Boore 等（2011）模型估算不同深度VS30时，存在系统性偏差，出现低估VS30现象，尤其是当深度小于15 m 时，低估现象较明显，随着钻孔深度的增加，偏差逐渐降低。对数线性模型、对数二次模型、对数三次模型仅在深度小于10 m 时，存在约3%的低估现象，可忽略不计。Boore 等（2011）模型与本文模型差异性说明场地速度模型具有区域性，速度模型是土体形成过程中物理性质的体现。因此，本文对数线性模型、对数二次模型、对数三次模型预测效果明显优于Boore 等（2011）模型。

（2）对数线性模型、对数二次模型、对数三次模型皮尔森相关系数基本一致，对数三次模型相对误差、残差标准差均较小。

（3）当雄安新区钻孔深度小于15 m 时，建议选择对数三次模型和本文给出的相应参数进行VSE30估算；当钻孔深度为15～20 m 时，建议选择对数线性模型和本文给出的相应参数进行估算；当钻孔深度大于25 m时，建议选择对数三次模型和本文给出的相应参数进行VSE30估算。因此，对数三次模型可在一定程度上为雄安新区缺少钻孔数据或钻孔剖面深度不足30 m 的VS30估算提供参考。

（4）在不同的VS30范围内，Boore 等（2011）模型的低估现象是全频段的，变化一致。而本文对数线性模型、对数二次模型、对数三次模型存在1 个分界点，即VS30=250 m/s，低于该临界值时出现高估现象，高于该临界值时出现低估现象。在高于临界值和低于临界值的2 个频段，随着钻孔深度的增加，VSE30以相反的趋势接近VS30，这可能是因为本文模型是基于理想状态下，土层密实和坚硬程度随着深度的增加呈线性递增，但实际情况呈非线性增加。