深度融合特征提取网络及其在化工过程软测量中的应用

周乐，沈程凯，吴超，侯北平，宋执环

（1 浙江科技学院自动化与电气工程学院，浙江 杭州 310024； 2 浙江大学工业控制技术国家重点实验室，浙江 杭州 310027）

引 言

近年来，随着现代流程工业的飞速发展，生产规模越来越庞大。然而，受到技术或预算的限制，现代流程工业中往往存在部分难以通过在线传感器直接进行检测的关键变量，尤其是关键的质量指标。因此，为了解决关键质量指标的估计和控制问题，软测量技术越发得到人们的重视。该技术建立易测的过程变量与难测的质量变量之间的数学模型，具有成本低、配置灵活、实时性好和维护简单等优点[1-3]。

软测量技术通常分为两大类，分别为机理模型和数据驱动模型。由于流程工业过程日趋复杂，建立准确的机理模型也愈发困难。随着传感器技术的高速发展以及集散控制系统的广泛应用，通过分析海量的现场数据，基于数据驱动的软测量技术得到了快速发展[4-5]。这项技术通过历史数据建立预测模型，无须先验知识和操作经验，在复杂流程工业监测与软测量领域得到了广泛的应用。目前，常见的数据驱动软测量技术主要包括多元统计方法和机器学习方法。常用的模型有主成分回归(principal component regression,PCR)、偏最小二乘回归(partial least squares regression, PLSR)、支持向量机(support vector machine, SVM)以及人工神经网络(artificial neural network,ANN)等[6-9]。

目前常用的数据驱动软测量技术绝大部分为静态建模方法，而实际的复杂流程工业过程观测数据往往包含很强的动态特性。为提取数据的动态特性或自相关特性，Ku 等[10]首次提出动态主成分分析(dynamic principal component analysis, DPCA)模型并用于过程监控，而动态偏最小二乘回归模型(dynamic partial least squares regression,DPLSR)被提出以预测动态过程数据[11-12]。Ge 等[13]提出了动态概率潜隐变量回归(dynamic probabilistic latent variable model,DPLVM)模型，在线性动态系统[14-15]的框架之下有效地捕捉数据的自相关性的特征，并用于工业过程在线监测以及关键质量变量预测。Zhou 等[16-17]提出了一种切换的自回归动态潜隐变量模型，并给出了模态切换的后验估计方法，用于解决多模态动态过程建模问题。然而，上述方法均属于线性建模方法，无法准确提取观测数据间的非线性相关关系。

针对非线性数据建模问题，常见的方法主要包括机器学习建模方法和神经网络模型。传统的非线性机器学习建模方法有核主成分分析(kernel principal component analysis, KPCA)、核最小二乘法(kernel partial least squares, KPLS)等[18-19]。近年来，神经网络模型，尤其是深度学习建模方法得到了快速发展。但是与传统的机器学习模型相比，基于深度学习的软测量技术仍存在一定的缺陷。其主要问题在于深度学习方法属于黑箱模型，无法准确描述模型的运作机制，可解释性差，从而增大了模型优化和超参数选择的难度。Kingma 等[20]提出了一种变分自编码器模型(variational autoencoder,VAE)，将变分贝叶斯模型与自编码器结构结合，利用神经网络学习变分推导的参数，并且对编码器添加约束，限制潜隐变量服从单位高斯分布，增强了模型的可解释性。VAE 模型能有效提取数据的深层非线性特征，已被广泛应用于流程工业过程建模与监控领域[21-22]。

此外，基于机器学习和深度学习技术，研究者初步研究了非线性动态建模问题。Odiowei 等[23]提出了典型变量分析与核密度估计相结合的方法，在典型变量分析模型的基础上，更新了相关变量的概率密度以及指标的估计方法，使其适用于非线性动态过程监控。Yuan 等[24]提出了基于有监督长短记忆网络建模的软测量方法(supervised long shortterm memory network,SLSTM)，同时利用过程变量和质量变量来构建LSTM网络。此外，考虑到观测数据同时存在互相关和自相关关系，Yuan 等[25]进一步提出了基于时空注意力机制的长短记忆网络模型(spatiotemporal attention-based long short-term memory,STA-LSTM)，通过给予每个变量不同的权重系数，可自适应地计算潜隐信息与质量变量的相关程度。Yao 等[26]提出了增量式动态特征提取及传递模型(incremental dynamic features extracting and transferring model,IDFETM)，在提取到非线性动态特征的同时，采用增量学习方法，使模型获得了快速吸收和优化历史信息的能力。另有一些学者基于现有的深度学习框架提出了一系列改进模型，有效提高了动态过程建模准确度和预测性能，并提高了模型鲁棒性[27-30]。此 外，Shen 等[31]在VAE 的 基 础 上 提 出 了 一种有监督非线性动态系统(supervised nonlinear dynamic system, SNDS)。该模型基于时间窗提取数据的动态特性，并利用VAE 模型，将传统的动态潜隐变量模型扩展至非线性概率形式，兼具动态潜隐变量建模方法和深度学习技术的优点，能有效提取非线性动态特征。在SNDS 中，虽然每个潜隐变量都被用于和相应的质量变量拟合训练，但在进行在线质量预报时，通常只使用最后一个潜隐变量进行质量预测。当针对强动态数据时，需设置较大的时间窗以提取完整的动态信息。虽然相邻潜隐变量间可进行有效的信息交互，但是该模型存在历史潜隐变量信息在传递过程中被稀释的问题。为解决上述问题，本文提出一种新的深度融合特征提取网络(deep fusion feature extraction network, DFFEN)。该方法在VAE 框架下构建非线性动态潜隐变量，同时，引入自注意力机制[32-33]融合时间窗内的所有动态潜隐信息，优化因时间窗过长而导致的动态潜隐特征被遗忘的问题。此外，在后端网络构建动态潜隐变量和关键质量变量之间的回归模型，以实现关键质量变量的预报。

本文提出深度融合特征提取网络及其相应的化工过程软测量方法，并通过实验验证本文提出方法的有效性。

1 有监督非线性动态系统（SNDS）模型回顾

SNDS 结合VAE 的框架，将线性动态系统扩展至非线性形式[31]，其结构可被表示为

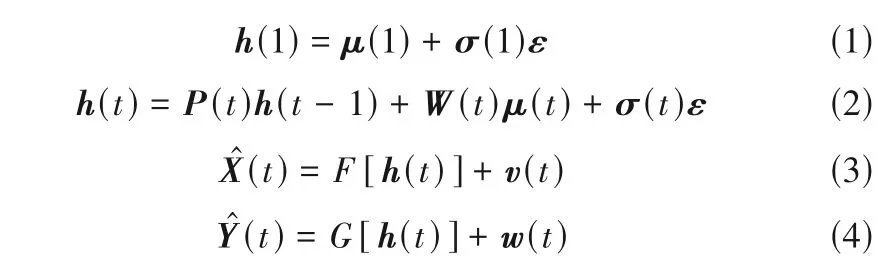
式中，h(t)是动态潜隐变量；转移矩阵P(t)用于构建h(t)和h(t- 1)之间的关系，以传递动态潜隐变量之间的自相关信息；转移矩阵W(t)用于计算第t个VAE 生成的均值μ(t)和当前潜隐变量h(t)之间的关系，以便通过重采样方式生成潜隐变量h(t)；Y^ (t)是重构的输出样本；和VAE 模型中的重构公式类似，F(*)和G(*)表示非线性变换过程，F(*)代表自编码器的解码过程，用于重构输入数据，而G(*)用于将生成的潜隐变量h(t)和输出变量样本数据拟合，从而构建回归模型，对关键质量变量进行预测；ε、v(t) 和w(t) 代表高斯噪声，其分布分别为ε～N(0,I)，v(t)～N(0,σ2xI)和w(t)～N(0,σ2yI)。

SNDS 的模型结构主要分为两个部分，分别是特征提取部分以及回归模型部分。首先通过多个相互连接的自编码器提取动态潜隐变量，再进行有监督训练，是一种可解释性较强的深度学习模型。

2 深度融合特征提取网络（DFFEN）模型及其软测量方法

2.1 DFFEN模型结构

虽然在处理非线性动态工业数据时，SNDS 能通过提取非线性动态信息实现对关键质量变量的预测，但仍存在一些不足之处。实际的化工过程数据往往具有较强的动态特性。针对强动态数据，需要构建长时间窗来描述数据的强自相关性。而当时间窗过长时，会导致较早时间的动态相关信息在传递时易被弱化，存在信息稀释的问题。为解决上述问题，本文提出了一种新的深度融合特征提取网络。该模型融合了自注意力机制[32-33]，通过计算时间窗内的动态潜隐变量权重，有效提取非线性动态数据的相关关系。

DFFEN的模型结构如图1所示。该模型主要分为两部分：前端网络进行自监督训练，用于获取融合后的动态潜隐变量信息；后端网络通过拟合潜隐变量与质量变量样本，完成有监督训练。前端与后端网络共同组成了一个完整的软测量模型。

图1 DFFEN模型结构Fig.1 Model structure of the DFFEN

作为一类动态特征提取网络，首先需要对样本进行预处理，采用滑动窗口策略对标准化后的时间序列样本进行划分。选择合适的模型长度T后，可以将过程变量以及质量变量样本各自划分为T组。

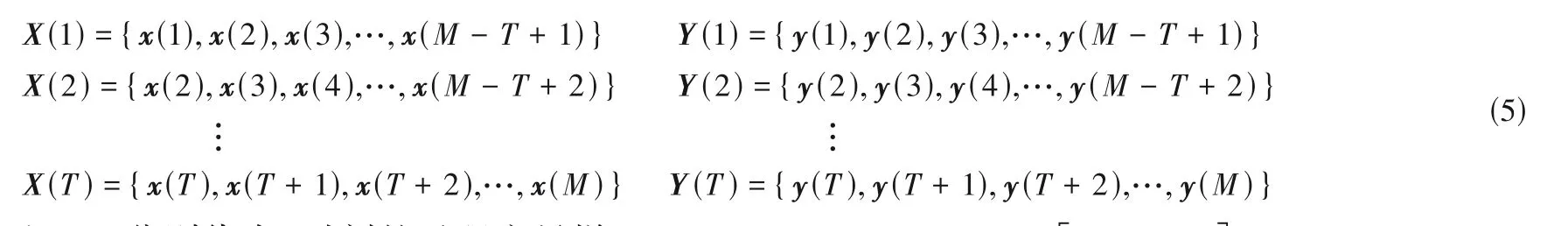
式中，x(t)和y(t)分别代表t时刻的过程变量样本以及质量变量样本；M为总样本大小。这种数据划分策略既能保护输入样本的时序性，又便于后续的动态建模过程。

DFFEN 的前端网络由T个相互连接的VAE 组成，每个自编码器负责产生对应的潜隐变量h(t)。当时间序列X(1)至X(T)作为训练集输入到前端网络训练完成后，得到相应的动态潜隐变量信息h(t)，其结构如式（6）所示。

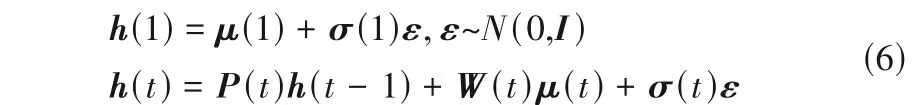
式中，t∈[2,T]；μ(t)、σ(t)以及ε分别代表第t个VAE 的均值、方差以及高斯噪声；P(t)为h(t)和h(t- 1)之间的转移矩阵；W(t)是系数矩阵，用于计算潜隐变量h(t)与均值μ(t)的相关关系。

通过重采样方式，第一个自编码器训练得到的参数μ(1)、σ(1)和ε可被用于构造潜隐变量h(1)。同理可得到h(2)至h(T)。而引入高斯噪声ε，有效提高了网络的鲁棒性。其中，动态潜隐变量之间的连接方式类似于信息传递链，通过累加的方式，潜隐变量信息由前向后传递。构建动态潜隐变量信息传递通道有利于提取完整的动态潜隐变量，为后续的有监督拟合提供了更加可靠的关键信息。

T个相互连接的VAE可用于产生相对应的潜隐变量h(t)，且信息传递链的构造使得潜隐变量包含了动态特性。然而，当实际工业过程数据包含了强动态相关性时，模型长度T往往很大，从而导致各VAE 提取到的动态潜隐变量信息随着信息传递过程而逐渐损失，以至影响潜隐信息提取效果以及后端网络预测精度。因此，网络结构[式(6)]在处理强动态相关工业数据时的建模效果会被削弱。

为改善上述问题，自注意力机制被用于融合时间窗内的动态潜隐变量信息。其结构如式(7)所示。

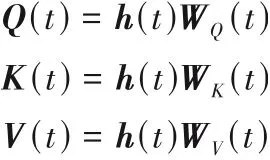
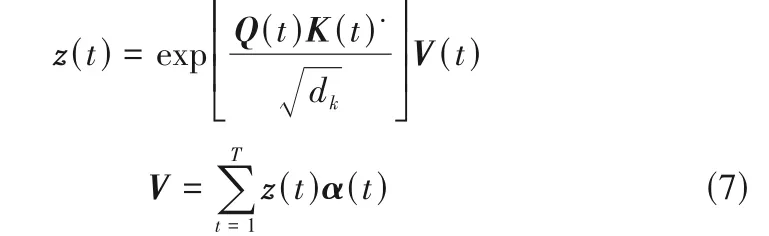
式中，Q(t)、K(t)和V(t)分别代表动态潜隐变量期望投影的向量空间，相应地，WQ(t)、WK(t)和WV(t)为各自的权重矩阵；dk为距离参数；z(t)代表t时刻潜隐变量变换后的输出。最后利用训练完成的系数α(t)整合所有变换后的动态潜隐变量信息，得到特征融合后的非线性动态潜隐变量V。之后，利用融合后的非线性动态潜隐变量进行解码，完成前端网络搭建。

在后端网络中，将提取到的动态潜隐变量信息和关键质量变量拟合，其结构如式(8)、式(9)所示。

式中，t∈[1,T]；F(*)和G(*)分别代表解码层以及拟合层的非线性变换过程；w1和w2为高斯噪声。

2.2 DFFEN网络损失函数

为估计DFFEN 的模型参数，首先需要确定模型的损失函数。VAE 的目的是生成服从原数据集分布的潜隐变量h(t)。根据VAE 的模型结构，可得出其边缘概率的对数似然函数方程。

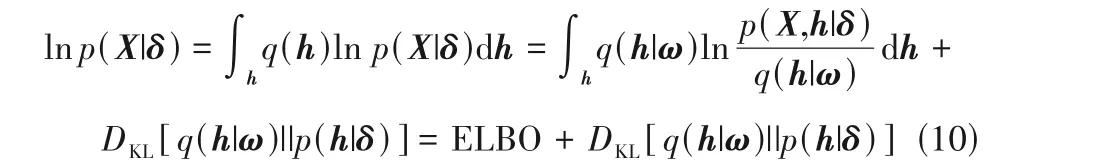
式中，X代表输入样本；h代表潜隐变量；q(h|ω)及p(X,h|δ)分别被定义为编码层和解码层的输出的概率分布；ω和δ分别为编码层和解码层的参数。通过推导可得VAE 的似然函数分为证据下界（evidence lower bound，ELBO）以 及 KL 散 度(Kullback-Leibler divergence)两部分。变分推断的目标是寻求一个概率密度函数q(h|ω)来近似p(h|δ)。以该优化方案为目标，需要使KL 散度最小，相当于最大化ELBO。

针对DFFEN 模型，其最大化联合概率函数的问题可转化为ELBO的最大化问题，该目标函数为

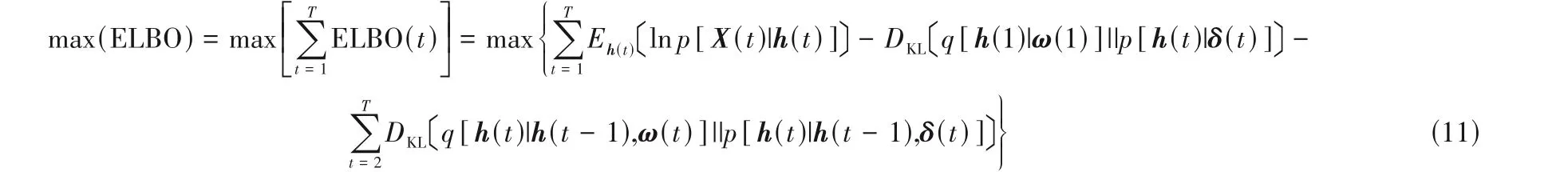
其中，第一项为后验分布期望值；第二、三项代表KL 散度。初始先验概率服从高斯分布为p[h(t)|δ(t)]=N(0,I)。随后动态先验分布满足p[h(t)|h(t-1),δ(t)]=N[P(t)h(t-1),I]。q[h(1)|ω(1)]及q[h(t)|h(t- 1),ω(t)]作为后验概率的估计值也服从高斯分布。由以上条件可得到DFFEN 模型的损失函数如式(12)所示。

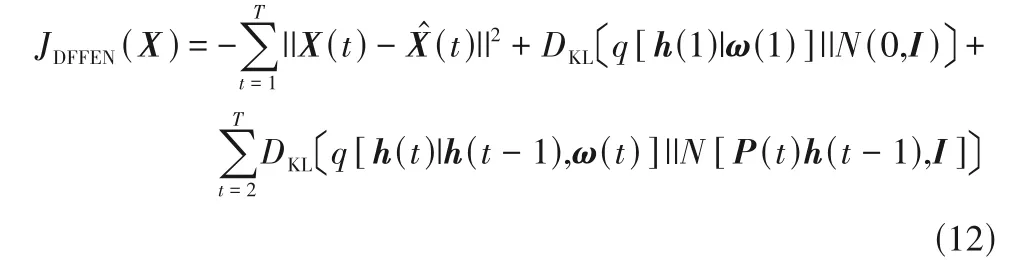
2.3 DFFEN优化器选择

为更高效地优化网络结构，须选择合适的优化函数。Adam 优化器因其计算高效、收敛速度快等优点，得到了广泛使用。Adam 优化器的梯度更新规则如式（13）所示。组成训练样本。

②将建模样本进行标准化处理后，利用滑动窗口策略，得到T组过程变量样本和T组质量变量样本。

③固定优化器为Adam 优化器，选择合适的训练次数、批次大小以及隐层数目，并设置合适的模型长度T以及动态潜隐变量维度。

④初始化DFFEN的模型参数。

⑤进行前端网络的训练。当损失不再降低时，保留模型参数。

⑥提取融合后的动态潜隐变量V，用于后端网络的训练。

⑦输入测试数据集，得到预测的质量变量样本Y^test(T)。

基于有监督DFFEN的软测量流程如图2所示。

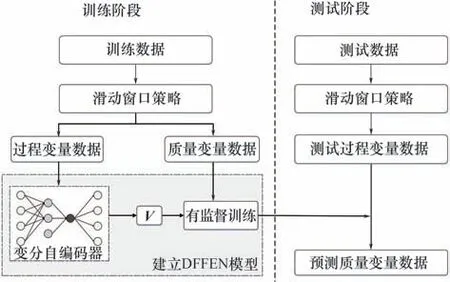
图2 基于DFFEN的软测量流程图Fig.2 Flow chart of DFFEN for soft sensing

2.4 基于有监督DFFEN的软测量

为预测最终的质量变量，需构建相应的回归模型。本文使用两层全连接网络进行有监督训练，其损失函数采用最小平方误差。

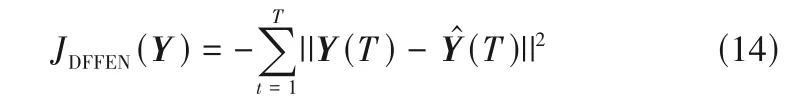
为评估软测量模型的性能，通常使用均方根误差(RMSE)和拟合优度R2两个指标。RMSE 和R2的计算公式如式(15)、式(16)所示。

前端网络的损失函数用于重构近似输入样本的同时，生成概率分布的近似值，以保证构造的非线性动态潜隐变量服从设定的分布。后端网络用于拟合潜隐变量信息和关键质量变量样本之间的输入输出关系。基于DFFEN 的化工过程软测量方法的具体步骤如下。

①收集化工过程的过程变量X以及质量变量Y

式中，yj代表第j个质量变量样本的实际值；y^j代表第j个质量变量样本的预测值；Nt代表样本数目；yˉt代表实际质量变量样本的均值。RMSE 用来表示样本实际值和预测值的平均平方差，R2用于描述样本预测值和实际值的匹配程度。模型性能越好，预测值越接近实际值，RMSE越小，R2越高。

3 实验案例

本节将通过一个数值案例和一个实际的合成氨生产过程验证基于DFFEN 的软测量方法的有效性。

3.1 数值案例

本节首先构建了一个非线性动态系统，其具体结构如式（17）、式（18）所示。

式中，h(t)代表动态潜隐变量；x(t)代表过程变量；y(t)代表质量变量。此外，为描述实际工业过程中包含的测量噪声，分别加入白噪声w1(t)、w2(t)和w3(t)，其中w1(t)和w2(t)是均值为0、方差为0.7 的高斯噪声；w3(t)是均值为0、方差为0.1 的高斯噪声。

利用上述非线性动态系统，本文共生成了1000 个样本。前500 个数据作为训练集，用于训练模型参数。后500 个数据作为测试集，用于评价模型预测性能。此外，本文还选择了概率主成分回归(probabilistic principal component regression, PPCR)模型、SNDS 和有监督堆栈自编码器(supervisedstacked autoencoder, SSAE)作为对比模型。DFFEN模型的隐层维度设置为n=8，拟合层的神经元数量设置为150 个。同时，对比模型SNDS 和SSAE 的隐层神经元个数也设置为n=8，拟合层神经元个数设置为150 个，其中SNDS 的模型长度T=4，SSAE 设置为三层特征提取层，PPCR 的潜隐变量维度设置为n=2。

为获取更有效的模型参数，本文测试了DFFEN在不同参数T设置下的预测性能。不同参数T下的多次实验平均评价指数如图3 所示。可以得出，当T=4 时，DFFEN 模型达到最佳性能。各模型在本数值案例的实验结果如表1所示。不同模型的软测量结果和预测误差如图4 和图5 所示。受到非线性数据结构的影响，线性模型PPCR 的预测效果最差。SSAE 通过提取深层特征进行有监督训练，SNDS 利用自编码器的架构提取到了动态潜隐变量，其模型预测精度均优于线性模型。而DFFEN 能够有效提取长时间尺度的非线性动态特征，模型预测效果最佳。

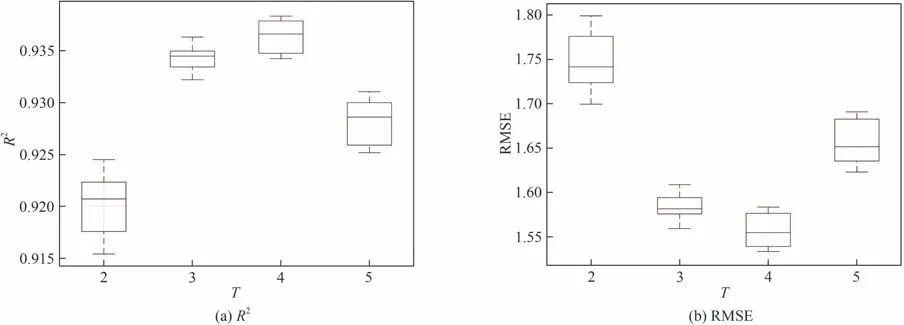
图3 T与评价指标R2和RMSE的关系Fig.3 The evaluation indices R2 and RMSE versus T

图4 数值案例中不同模型的软测量结果Fig.4 Soft sensing results for different models in the numerical case

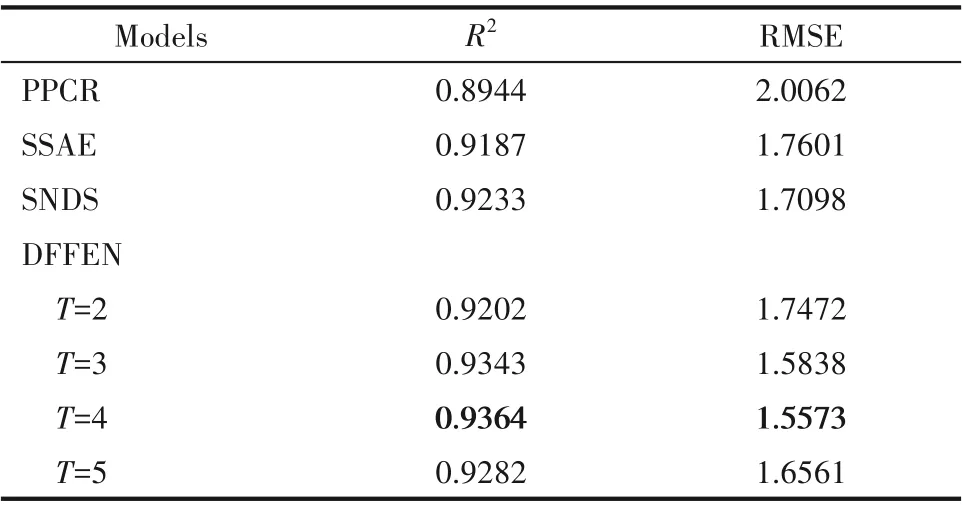
表1 数值案例不同模型预测结果Table 1 Prediction results for different models using numerical case

3.2 合成氨生产过程

在合成氨生产过程中，氢气是主要原料之一。通常以甲烷作为原料，经过甲烷转化装置得到高纯度氢气。该装置包括预转化炉、一段转化炉和二段转化炉。其中一段转化炉的装置流程如图6 所示。根据反应机理，塔中的反应温度是炉内制氢的关键。只有充足的燃气资源才能确保反应顺利进行。因此，准确地测量炉内的氧含量对于降低生产成本同时保证氢气的纯度以及产量尤为重要。

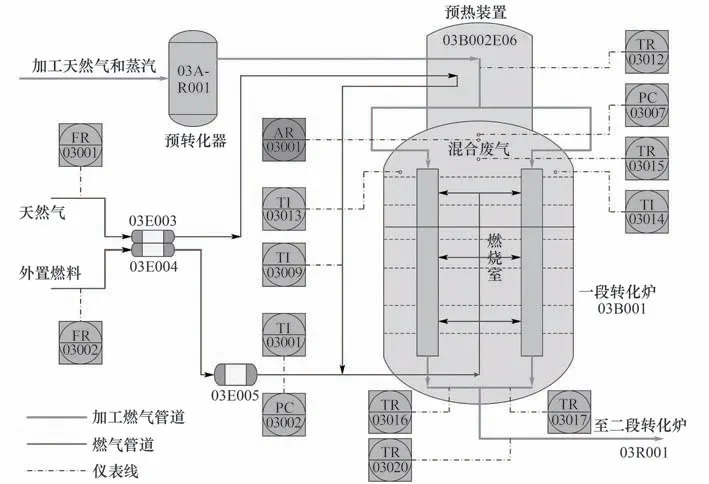
图6 一段转化炉流程图Fig.6 The flowchart of primary reformer

本文选择了一段转化炉中的13个易测的辅助变量作为输入，炉顶的氧浓度作为被预测的关键质量变量。各变量的具体描述如表2所示。本文共使用20500 个样本进行模型训练和测试。其中20000 个样本作为训练集，另外500 个样本作为测试集验证模型的预测性能。此外，继续选择SNDS、PPCR 和SSAE作为对比模型。

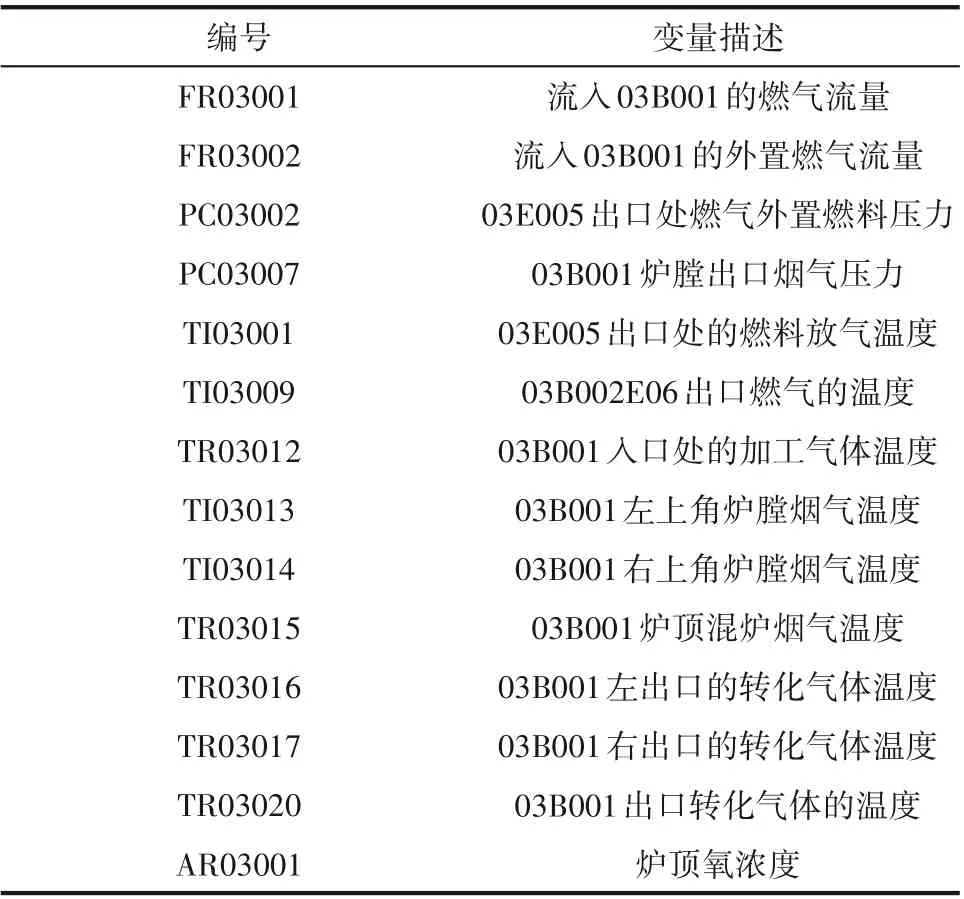
表2 一段转化炉变量描述Table 2 The description of the variables in primary reformer

由于实际的生产过程具有较强的动态特性，DFFEN 的模型长度T需要设置得较大，经过性能测试，T的值设置为33，隐层维度为11，拟合层为2 层，其中神经元个数为150 个。SNDS 的模型长度设置T=33，同样地，拟合层设置为2 层，神经元个数为150 个。SSAE 的特征提取层设置为3 层，各层神经元个数设置为n=11，拟合层和DFFEN 及SNDS 相同。PPCR 的潜隐变量个数设置为n=11。不同模型在合成氨过程的预测结果如表3 和图7 所示。可以看出，DFFEN 的预测精度最高，特别是250～500 样本区间。SSAE虽然也有较好的预测能力，但只是大致反应质量变量的变化趋势，无法对其进行精确预测。SNDS 的预测值虽然能够反映大致趋势，但是波动极大，与实际值存在较大误差。此外，由于PPCR 为静态线性模型，不适用于非线性动态建模，拟合效果过差。图8 展示了4 种模型的预测误差。如图所示，DFFEN 的预测误差较另外3 种模型更接近于0，误差更小。而PPCR、SSAE 和SNDS 的预测误差明显偏高，尤其在1～100样本区间内最为明显。因此，对比其余3种模型，DFFEN的预测值更接近实际值，性能最优。

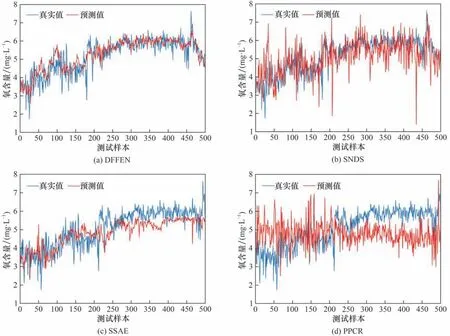
图7 各模型在合成氨过程的预测结果Fig.7 Prediction results for different models in the synthetic ammonia process

图8 各模型在合成氨过程中的预测误差Fig.8 Prediction error for different models in the syntheticammonia process

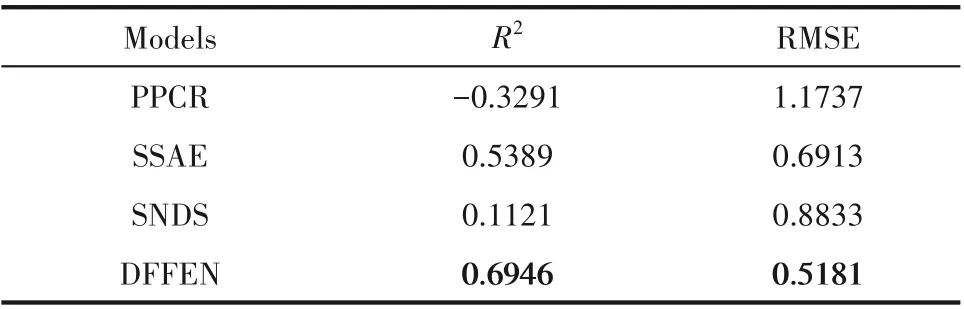
表3 各模型在合成氨过程的预测结果Table 3 Prediction results for different models in the synthetic ammonia process

4 结 论

针对复杂化工过程的非线性和强动态特性，本文提出了一种新的深度融合特征提取网络。该模型在变分自编码器的框架下提取非线性潜隐变量，并通过构造信息传递链捕获动态特征。利用信息融合的方法，融合后的潜隐变量克服了动态相关信息在传递过程中被稀释的缺陷，有效提高了模型的预测精度。通过数值案例以及实际的合成氨生产过程验证了所提出方法的有效性。实验结果表明，该模型能够有效处理复杂化工过程的非线性强动态数据，模型预测效果较好，同时该模型具有较好的扩展性，具备良好的应用前景。