基于双部分丢弃的模拟移动床产率提高策略

魏朋，陈珺，王志国，刘飞

（江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122）

引 言

模拟移动床(simulated moving bed,SMB)色谱技术是化学工程中一种重要的分离纯化技术，该技术主要是利用进料中各组分与固定相吸附剂的亲和力差异来实现组分间的分离[1]。传统的模拟移动床装置由多个带有样品进出口的色谱柱通过多位阀和管道串联而成，并通过周期性地切换多位阀以实现固定相与流动相相对于进出料口的反向运动。自20世纪60年代Broughton等[2]提出以来，模拟移动床技术因具有传质驱动力大、分离能力强、洗脱液消耗少和可连续化生产等特点[3]，其应用领域已从石油化工、制糖工业扩展到生物制药、精细化工等行业[4-7]。

模拟移动床分离过程的工艺复杂，其分离性能(如纯度、产率和回收率等)由多个工艺参数共同决定，且不同分离性能之间存在很强的竞争关系[8]。因此，如何提高分离性能一直是模拟移动床分离过程的研究重点之一。提高分离性能的解决策略主要归纳为两种，一种是根据对性能参数的不同要求通过多目标优化算法寻找工艺参数的Pareto 最优解。如Minceva 等[9]在对二甲苯的分离过程中采用两级优化策略，实现了以尽可能小的洗脱液消耗获得最大产率的目标；胡蓉等[10]采用多目标教学优化算法实现了对二甲苯回收率和纯度的同时最大化；Matos 等[11]在双萘酚对映体的分离过程中采用并行粒子群优化算法，实现了产率的最大化和洗脱液消耗的最小化。另一种是基于传统的模拟移动床工艺开发新的操作策略，如可改变每区色谱柱数量的Varical 策 略[12]、调 节 进 料 流 量 的PowerFeed 策 略[13]、调节进料浓度的Modicon 策略[14]、间歇模拟移动床[15]、三区模拟移动床[16]和部分丢弃(partial-discard,PD)策略[17]等。其中，PD 策略工作原理为在每个切换周期的初始阶段丢弃一部分含杂质(弱吸附组分)的提取产品或最后阶段丢弃一部分含杂质(强吸附组分)的提余产品以提高产品的纯度。虽然PD 策略能够提高产品的纯度，但丢弃的高浓度产品会造成产品回收率的较大损失。为了改善此策略，即在确保产品高纯度的同时尽可能地减小产品回收率的损失，又有学者提出了分馏和反馈策略[18]、回收部分丢弃策略[19]、功率部分丢弃策略[20]、全回收部分丢弃策略[21]和带产品柱的策略[22]等。

上述的两种解决策略虽然从不同的角度出发提高了分离性能，但其多是基于平衡理论[23-24]这一理想设计工具的，即在完全分离区域内寻找期望的工艺点(包括入口和出口处的流量)，这会限制进料流量的选取范围，进而限制了模拟移动床的产率。此外，文献[22]中提出的带产品柱的策略建议将模拟移动床丢弃的产品流通入到一个特殊的产品柱中，通过合理设计该产品柱的柱长、流速和吸附剂性质等可实现丢弃流中两产品的有效分离，但该策略需要研发具有高吸附容量和分配系数的新型吸附剂，这是一个耗时且成本较高的过程。

针对在完全分离区域内选取工艺点导致的产率受限这一问题，在保证产品纯度的情况下，本文提出一种旨在提高模拟移动床产率的带额外色谱柱的双部分丢弃(extra-column and binary-partialdiscard，EC-BiPD)策略。首先，该策略在一定程度上突破了平衡理论中完全分离区域的限制，即在保证提取产品纯度合格的情况下，通过增大进料流量将工艺点选取在纯提取产品和非纯提余产品区域。然后，把在每个切换周期最后阶段含较多杂质的提余产品暂时丢弃，并作为进料通入到一个额外色谱柱(extra-column, EC)中以进一步分离，然而该额外色谱柱只收集纯度达到一定要求的产品(称为额外产品)，其余部分被永久丢弃。最后，把在模拟移动床和额外色谱柱处分别收集到的产品混合得到总产品，并分析额外产品的积分纯度阈值对总产品性能参数的影响。

1 带额外色谱柱的双部分丢弃策略的原理

1.1 平衡理论

Mazzotti 等[23]提出的平衡理论促进了模拟移动床技术的快速发展和广泛应用，该理论为工艺点的选取提供了理论指导。经证明，在线性吸附等温线情况下，二元混合物完全分离的条件为：

式中，Qj为模拟移动床在j区的体积流量；ts为切换时间；ε为色谱柱的空隙率；VC为色谱柱的体积。

根据式(1)，可将mⅡ-mⅢ平面划分为图1 所示的不同分离区域，其中由w、a和b三点确定的区域为两组分的完全分离区域。当工艺点选取在该区域内时，获得的两产品的纯度接近100%。在完全分离区域的正上方为纯提取产品和非纯提余产品区域，当工艺点选取在该区域内时，获得的提取产品的纯度接近100%，而提余产品的纯度一般较差。于是可以根据不同的分离区域，大概确定分离过程的工艺点。

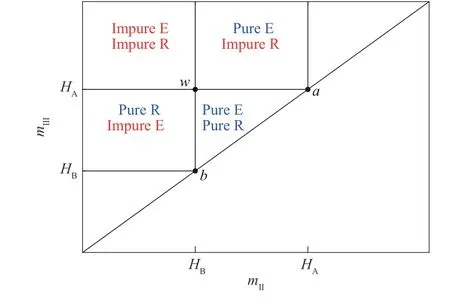
图1 线性吸附等温线描述的系统在mⅡ-mⅢ平面上的不同分离区域Fig.1 Different separation regions on the mⅡ-mⅢplane of the system described by linear adsorption isotherms

提高模拟移动床分离过程的产率，最直接的方式就是增加进料流量，但若进料流量的增加超出了色谱柱的吸附容量，那么会有更多的强吸附组分随提余产品排出，使提取产品的回收率和提余产品的纯度都降低。若进一步增加进料流量，那么含有弱吸附组分的再生洗脱液会穿越过渡区，使提取产品的纯度降低。考虑到后续的简便设计，本文在确保提取产品纯度合格的情况下，通过增大进料流量，使工艺点从初始的完全分离区域移动至纯提取产品和非纯提余产品区域。然而，此操作会损失提余产品的纯度，接下来需要进一步分离含有杂质即强吸附组分的提余产品。

1.2 双部分丢弃

模拟移动床经过多次切换达到循环稳态，此时产品的浓度呈周期性变化。以图2所示的提余产品的浓度变化为例，由于之前增大进料流量损失了提余产品的纯度，可以发现强吸附组分主要从每个切换周期的最后阶段流出，这也是造成提余产品纯度不合格的原因。

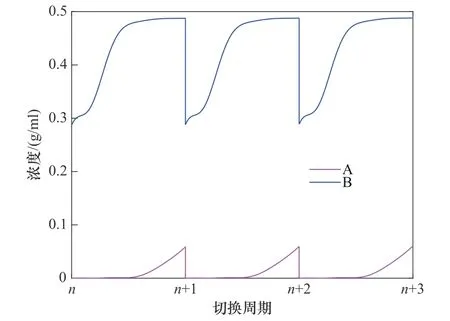
图2 在模拟移动床的循环稳态下提余产品的浓度变化（A为强吸附组分,B为弱吸附组分）Fig.2 The change of the concentration of the raffinate products under the cyclic steady state of the simulated moving bed

提余产品在分离出来之前，根据其最终用途需要特定的纯度。如图3 所示，由于在切换周期各时刻的提余产品的纯度(称为微分纯度)是不同的，故在此定义一个积分纯度的概念。例如，提余产品的积分纯度定义为从切换周期的初始时刻(τ=0)开始收集提余产品到收集结束(τ=τend)时提余产品的累积纯度，其中τ为以一个切换周期为基础定义的无量纲时间，其在0～1之间变化，如式(3)所定义。现假设所需提余产品的纯度为98.00%，从图3 可以看出，提余产品在整个切换周期的积分纯度为97.32%，低于所需要的纯度。若在τ为0.93 时就停止收集提余产品，那么提余产品的积分纯度正好为98.00%，且τ越小积分纯度就越大，但这会损失大量高浓度的提余产品，影响提余产品的回收率。因此，可根据积分纯度来决定何时停止收集提余产品并把其余部分丢弃。本文提出的操作策略建议把τend之前的提余产品收集，把τend之后的提余产品暂时丢弃。

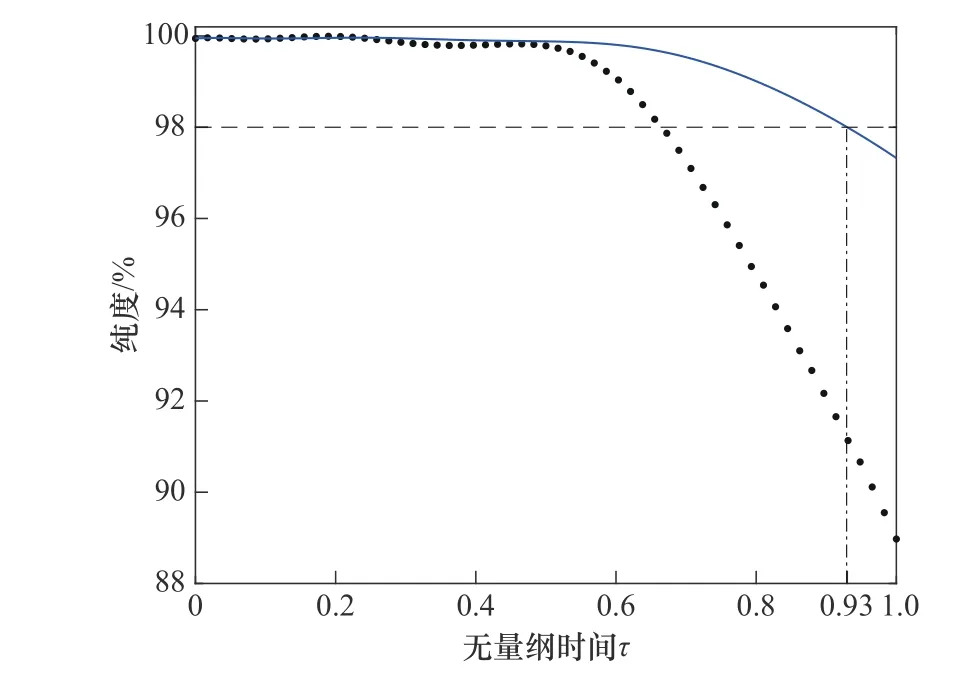
图3 提余产品的纯度变化（蓝色实线表示积分纯度,黑点表示微分纯度）Fig.3 Purity change of raffinate products

τ=t/ts,0 ≤τ≤1 (3)

为补偿提余产品回收率的损失，本文提出的操作策略在模拟移动床提余产品的出口处增加一个缓冲罐，用于收集上一步中丢弃的提余产品。当一个切换周期中需丢弃的提余产品在缓冲罐中收集完毕时，将其混合均匀并作为进料注入到一个额外色谱柱中，并称这部分进料为循环进料，然后用洗脱液冲洗该额外色谱柱。定义额外色谱柱在进料阶段与洗脱液阶段的总时长为一个注入周期，其大小等于模拟移动床的切换周期，以保证整个分离过程的连续运行，如图4 所示。考虑到成本与简便设计，此额外色谱柱和模拟移动床的色谱柱具有相同的规格，如相同的柱长、直径和固相吸附剂等。

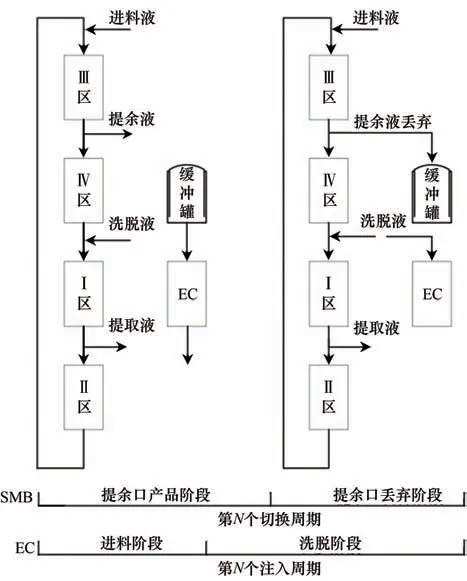
图4 EC-BiPD策略的操作示意图Fig.4 Schematic diagram of the EC-BiPD strategy

单个色谱柱很难有效分离亨利系数相差不大的两组分，这会导致弱吸附组分B 后沿的出口浓度与强吸附组分A 前沿的出口浓度重叠较为严重，如图5所示。但如果在额外色谱柱的进料中两组分的浓度相差较大，那么产品的出口浓度也会相差较大。所以仍能够以积分纯度为指导，在每个注入周期的初始阶段收集一部分指定纯度的产品B和最后阶段收集一部分指定纯度的产品A，这里收集到的产品A和产品B分别称为额外产品A和额外产品B。值得注意的是，额外产品A 的积分纯度定义为从每个注入周期的末尾时刻开始反向累积产品，直到累积纯度低于所要求的为止。在中间阶段两产品出口浓度重叠较严重的部分被当作杂质永久丢弃，注意此处杂质的永久丢弃是指相对于整个分离过程而言其不会再单独作为进料进行分离，但仍可将其与上游生产的待分离混合物进行混合并作为其他分离过程的进料，从而保证生产的经济效益。于是从额外色谱柱的出口处依次流出的为额外产品B、杂质和额外产品A。下一注入周期重复相同的操作，额外色谱柱可实现连续化生产。

图5 在一个注入周期中额外色谱柱的出口浓度示意图（虚线表示每个注入周期中进料阶段和洗脱阶段的分界线；操作条件:进料中组分A和B的浓度分别为1.17和2.35 g/ml）Fig.5 Schematic diagram of outlet concentration of the extra column during an injection cycle

2 分离过程的建模

2.1 模型描述

已有学者开发出不同复杂程度的色谱柱模型来研究模拟移动床的分离过程，如理想模型、平衡扩散模型、传质扩散模型和一般速率模型[25]等。由于本文研究的主要目的是验证所提策略的可行性，为简单起见，本文选取色谱柱的平衡扩散模型，该模型最大的特点为各组分在固定相与流动相之间的平衡是瞬间完成的[26]。

(1) 在平衡扩散模型中，流动相的质量守恒方程为：

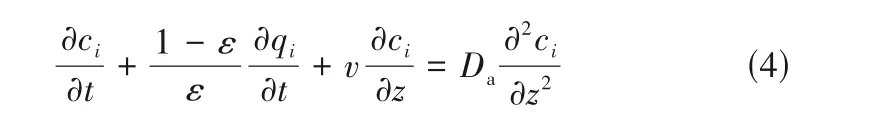
式中，ci、qi分别为组分i(i=A,B)在流动相与固定相中的浓度；v为流动相的流动速度；Da为表观轴向扩散系数；z、t分别为空间和时间坐标。

(2)线性吸附平衡方程为：

提取液出口节点处

QⅡ=QⅠ-QE,couti,Ⅰ=cini,Ⅱ=ci,E(10)

进料入口节点处

QⅢ=QⅡ+QF,couti,ⅡQⅡ+ci,FQF=cini,ⅢQⅢ(11)

提余液出口节点处

QⅣ=QⅢ-QR,couti,Ⅲ=cini,Ⅳ=ci,R(12)

式中，Qk(k= D,E,F,R)为洗脱液、提取液、进料和提余液的体积流量；cout/ini,j为组分i在j区的出口浓度或入口浓度；ci,k(k= D, E, F, R)为组分i在洗脱液、提取液、进料和提余液中的浓度。

(5) 额外色谱柱的数学模型同样可由式(4)～式(8)构成。模拟移动床与额外色谱柱连接处的平衡方程为：

式中，tF,EC、QF,EC、ci,F,EC分别为额外色谱柱的循环进料时长、循环进料流量、循环进料中组分i的浓度；tR,discard、cˉi,R,discard分别为模拟移动床提余口丢弃阶段的时长、组分i的平均浓度。

2.2 性能参数

评估模拟移动床分离过程的性能参数有纯度、回收率和产率等。本文研究了EC-BiPD 策略对这些性能参数的影响，并与传统的SMB 和PD 策略进行了比较。在模拟移动床循环稳态下的一个切换周期内，这些性能参数的定义如下。

(1)为了便于后续的表示，首先定义如下几个参数(单位：g)：在SMB提取口的产品阶段得到的组分i的质量

式中，tE,product、tR,product分别为模拟移动床提取口和提余口产品阶段的持续时间；tinitial,EC、tlast,EC分别为额外色谱柱初始阶段和最后阶段的持续时间；Qinitial,EC、Qlast,EC分别为额外色谱柱初始阶段和最后阶段的体积流量；cˉi,E,product、cˉi,R,product分别为在模拟移动床提取口和提余口的产品阶段组分i的平均浓度；cˉi,initial,EC、cˉi,last,EC分别为在额外色谱柱的初始阶段和最后阶段组分i的平均浓度。

(2)纯度Pu（单位：%）。纯度反映产品的质量，其定义为在一个切换周期内，产品流中收集到的目标产品的量与收集到的两产品总量的比值。

产品A的纯度为：

(3)回收率Re（单位：%）。对于增值产品而言，在生产待分离的混合物时就已经进行了大量投资，所以目标产品的回收率是很重要的。回收率反映进料的利用情况，其定义为在一个切换周期内，产品流中收集到的目标产品的量与进料中该产品总量的比值。

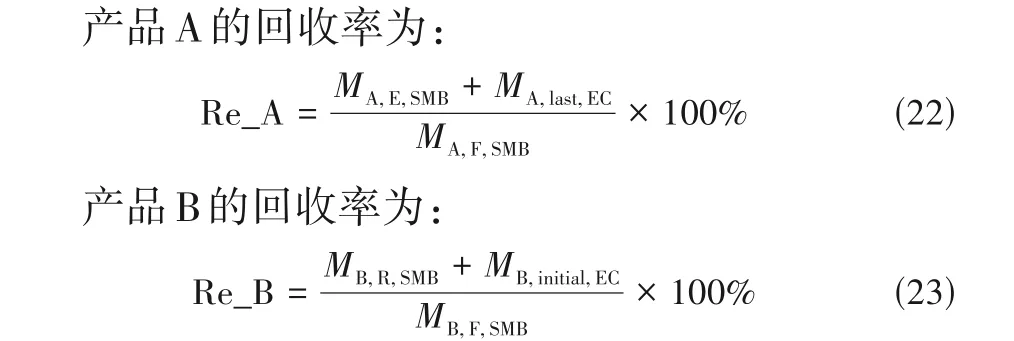
(4) 产率Pr [单位：g/（ml·p），p 为切换周期的单位]。产率反映分离过程的效率，是很关键的一个经济指标，其定义为单位体积吸附剂在一个切换周期内所得到的两产品的总质量。

2.3 模型参数

本文提出的EC-BiPD 策略以8 柱4 区结构的传统模拟移动床为主体分离装置，以额外色谱柱为补充分离装置，并采用色谱柱的平衡扩散模型来模拟实际的分离过程。由于本文只是通过仿真来研究所提策略的可行性，故只采用文献[27]中的模型参数和初始工艺参数，不针对具体的分离对象，所有的参数如表1所示。由于额外色谱柱与模拟移动床的色谱柱具有相同的规格，故在此不再单独列出其模型参数。

表1 模拟移动床的模型参数及初始工艺参数Table 1 Model parameters and process parameters of the simulated moving bed

3 结果与讨论

3.1 确定新工艺点

为提高模拟移动床的产率，同时考虑到对色谱柱中总压降的要求，现将模拟移动床的进料流量从初始工艺点处的0.0200 ml/s 提高到新工艺点处的0.0300 ml/s，Ⅰ区和洗脱液的流量保持不变。根据模拟移动床在节点处的平衡模型即式(9)～式(12)和流量比关系即式(2)可推导出式(26)，可以发现新工艺点处的流量比关系(mⅡ,mⅢ)为mⅡ-mⅢ平面上的一条直线，如图6中的黑色虚线Lnew所示。

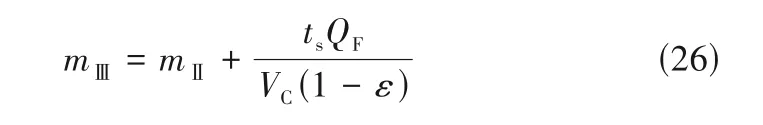
由于本文提出的操作策略将工艺点选取在纯提取产品和非纯提余产品区域，故在该区域的虚线Lnew上选取一组工艺点。基于流量泵的实际控制精度，最终选取了26 个均匀分布的工艺点，如图6 中的蓝点所示。表2总结了模拟移动床依次运行在这26 个工艺点时所获得的性能参数(这里只考虑纯度和回收率)，可以看出，随着mⅡ或mⅢ的增大，提取产品的纯度升高而回收率下降；相反，提余产品的纯度下降而回收率升高。根据两产品的实际用途，现假定所需的纯度均为98.00%。考虑到分离过程中提取产品纯度的鲁棒性，同时兼顾回收率的要求，本文选取这组工艺点中的第3 个(mⅡ= 0.2950,mⅢ=0.5589)作为新工艺点。

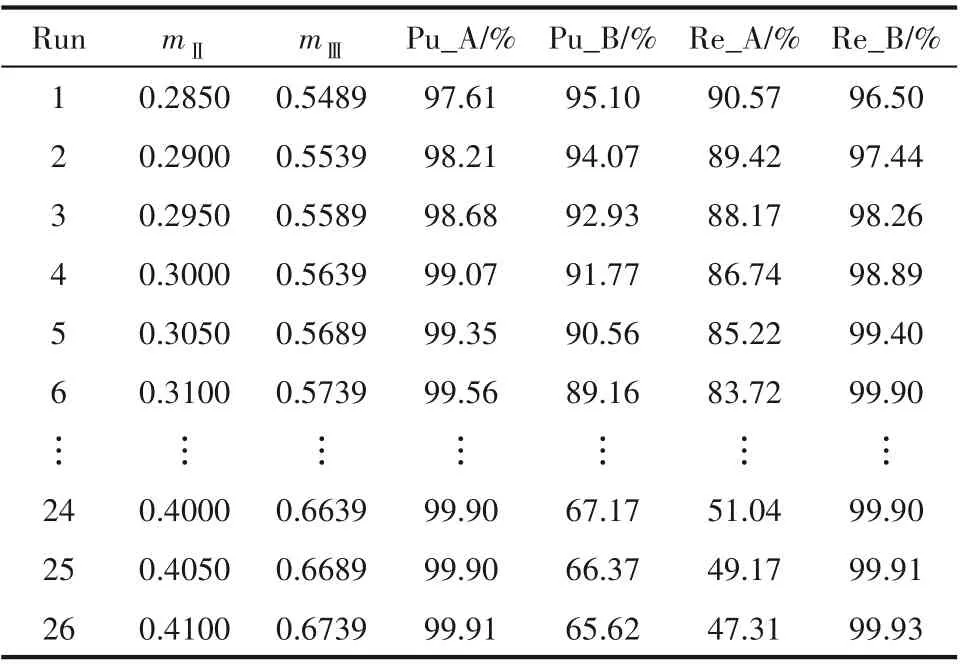
表2 模拟移动床运行在新工艺点时所获得的性能参数Table 2 The performance parameters obtained when the simulated moving bed runs at the new process point

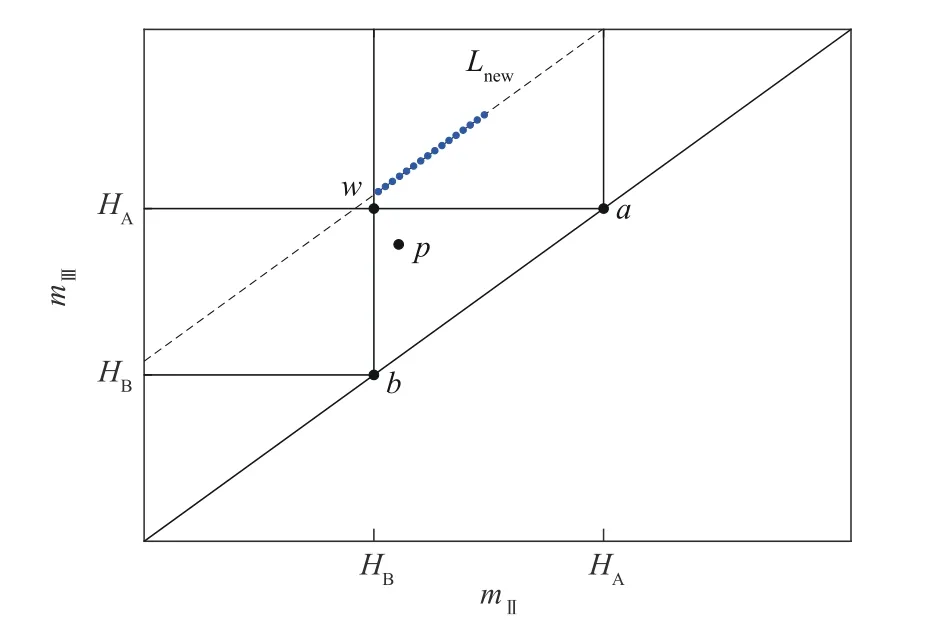
图6 新工艺点处的流量比(mⅡ,mⅢ)在mⅡ- mⅢ平面上的分布（p点表示初始工艺点,蓝点表示一组提高产率的工艺点）Fig.6 The distribution of the flow ratio(mⅡ,mⅢ)on the mⅡ- mⅢplane at the new process point

模拟移动床运行在该新工艺点时，其经过51次切换达到循环稳态，此时提余产品的出口浓度如图7 所示。从图7 可以看出，在循环稳态下的每个切换周期的最后阶段，提余产品中含有较高浓度的杂质(强吸附组分A)，这会影响提余产品的纯度和提取产品的回收率。因此，接下来需要利用部分丢弃策略来处理这部分含有高浓度杂质的提余产品。

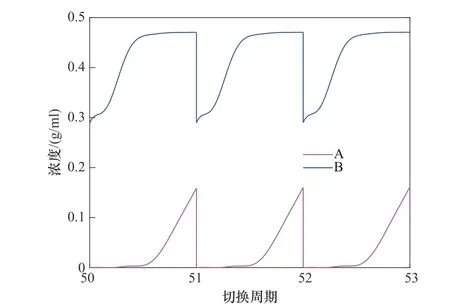
图7 模拟移动床运行在新工艺点时得到的提余产品的浓度Fig.7 The concentration of the raffinate products obtained when the simulated moving bed runs at the new process point

3.2 部分提余产品的暂时丢弃

模拟移动床运行在新工艺点下到达循环稳态后，其在一个切换周期中提余产品的积分纯度如图8 所示。不难发现，在提余产品的收集截止时间τend从0 增大到1 的过程中，其积分纯度从接近100%不断下降至92.93%，相应得到的提余产品的纯度也由合格变为不合格。值得注意的是，提余产品的积分纯度为98.00%时的τend为0.74，此时刚好满足3.1 节中假定的对提余产品纯度的要求。于是可根据部分丢弃策略，把τend之后的提余产品丢弃，此时提余产品的回收率仅为69.91%。被丢弃的提余产品虽然不符合纯度的要求，但其中含有大量高浓度的产品，所以该部分只是暂时丢弃并收集在一个缓冲罐中，然后作为进料通入到一个额外色谱柱中以进一步分离。

由于单个色谱柱很难有效分离亨利系数相差不大的两组分，再考虑到对产品回收率的要求，所以单个色谱柱只能收集到一定量的纯度达不到98.00%的额外产品A和额外产品B。本文通过提高提余产品的积分纯度阈值，以提高获得的提余产品的纯度。然后利用高纯度的提余产品来补偿纯度不达标的额外产品B，总产品B 的纯度为两部分产品混合后的纯度。在98.00%～99.60%之间选取一组均匀分布的数据作为提余产品的积分纯度阈值，提余产品在这组纯度阈值下进行部分丢弃后的性能参数如表3所示。

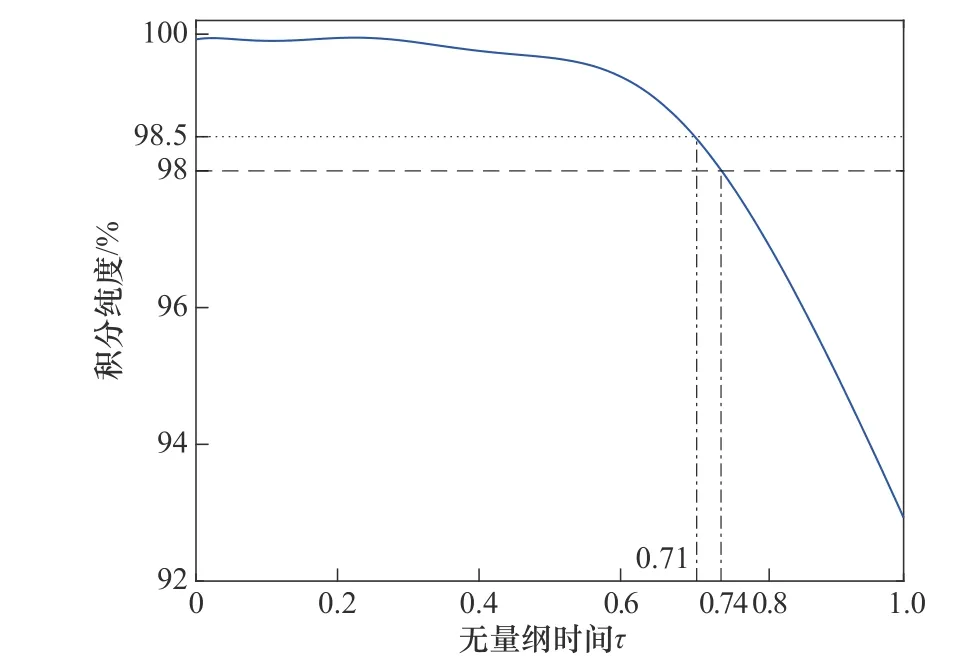
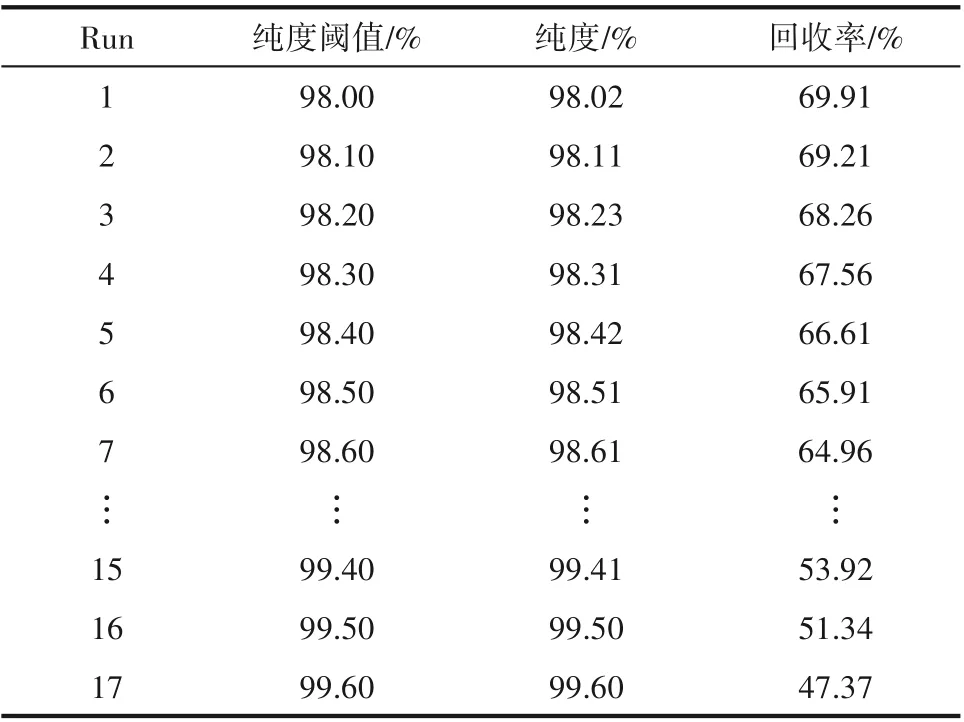
表3 提余产品在不同纯度阈值下进行部分丢弃后的性能参数Table 3 Performance parameters of raffinate products after partial-discard under different purity thresholds

从表3 可以看出，随着设置的提余产品积分纯度阈值的增大，提余产品的纯度会相应升高，但其回收率会有明显下降。综合考虑提余产品的纯度与回收率这两个性能参数，最终设置提余产品的积分纯度阈值为98.50%，此时的τend为0.71，如图8 所示。在满足纯度要求的提余产品收集完毕后，其余提余产品被收集在一个缓冲罐中并作为下面额外色谱柱的循环进料，此时循环进料中组分A 的浓度为0.0939 g/ml，组分B的浓度为0.4691 g/ml。

3.3 部分额外产品的永久丢弃

本文选取的额外色谱柱与模拟移动床的色谱柱具有相同的规格。首先设置循环进料的流量与模拟移动床在吸附区的流量保持相同，当循环进料注入完毕，然后在注入周期的其他时间内用洗脱液冲洗该额外色谱柱。如此循环往复，该额外色谱柱可实现连续生产。

图9为额外产品的出口浓度示意图，不难发现，两额外产品的浓度虽有较大部分的重叠但相差也较大。此外，在每个注入周期的前期，会有大量相对纯净的洗脱液流出，可以把这部分洗脱液收集起来循环使用，以减少洗脱液的消耗。根据之前定义的积分纯度计算出两额外产品的积分纯度，如图10所示。可以看出，从额外色谱柱流出产品的时刻即τpro开始，额外产品B 的积分纯度由100%逐渐降至83.37%；从τ=1 到τpro的累积过程中，额外产品A 的积分纯度变化幅度较大，由100%降至16.63%。于是通过设置两额外产品的积分纯度阈值，以计算出额外产品B的收集截止时间和额外产品A 的收集开始时间，其余时间内的产品被当作杂质永久丢弃。最后将额外产品A 和额外产品B分别与之前得到的提取产品和提余产品混合，根据式(20)～式(24)计算总产品的性能参数。

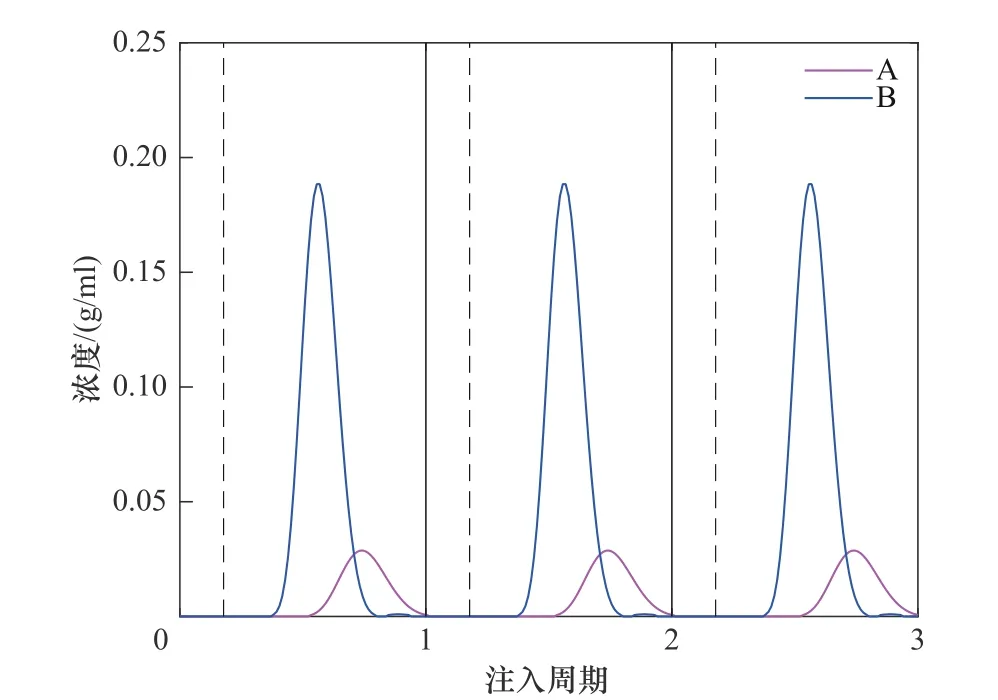
图9 额外产品的出口浓度示意图（实线表示相邻两个注入周期的分界线；虚线表示每个注入周期中进料阶段和洗脱阶段的分界线。操作条件:以表3中Run6下丢弃的提余产品作为额外色谱柱的进料）Fig.9 Schematic diagram of outlet concentration of extra products

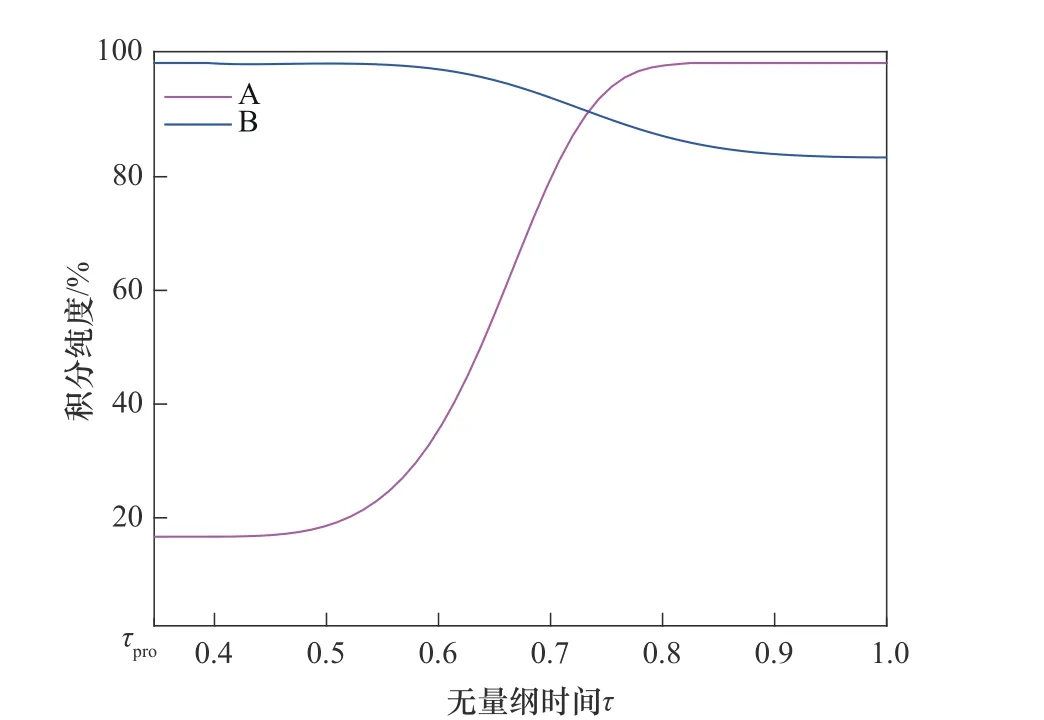
图10 额外产品的积分纯度（操作条件:以表3中Run6下丢弃的提余产品作为额外色谱柱的进料）Fig.10 Integral purity of extra products

图11 分析了额外产品的积分纯度阈值对总产品纯度和回收率的影响。从图11(a)可以看出，在额外产品A 的积分纯度阈值从90.00%逐渐增大到98.00%的过程中，产品A 的纯度不断变大且始终高于98.00%，这是因为之前获得的大量纯度高于98.00%的提取产品弥补了此处纯度未达到98.00%的额外产品A。另外，产品A 的回收率从91.98%不断下降，但也都高于90.50%。因此，可将额外产品A 的积分纯度阈值设置为90.00%，以使产品A 能够在满足给定的纯度要求下获得最大回收率。从图11(b)可以看出，当额外产品B 的积分纯度阈值小于96.40%时，产品B 的纯度始终小于98.00%，此时获得的产品B 不合格。只有当额外产品B 的积分纯度阈值设置为96.40%及以上时，产品B 才能达到所要求的纯度(虚线上方的部分)，相应的回收率会降至94.32%以下(点线下方的部分)。因此，可将额外产品B 的积分纯度阈值设置为96.40%，以使产品B 能获得最大的回收率。此时，根据式(25)可知，模拟移动床分离过程的产率也达到最大。

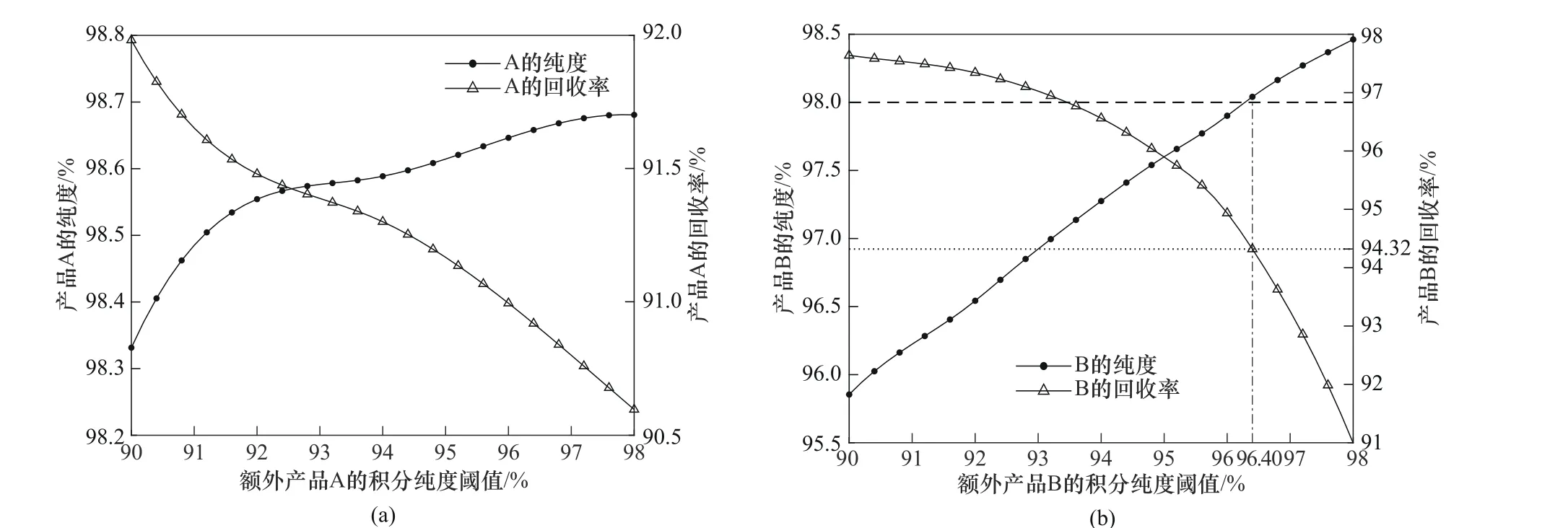
图11 额外产品的积分纯度阈值对总产品性能参数的影响Fig.11 Effect of integral purity threshold of extra products on performance parameters of total products

表4总结了本文提出的EC-BiPD策略、传统SMB工艺和PD 策略获得的性能参数。可以看出，ECBiPD策略获得的产品A和产品B都能满足98.00%的纯度要求且都能以较高的回收率回收进料，虽然与传统SMB 工艺相比稍有不足但优于PD 策略。最重要的是，与传统SMB 工艺相比EC-BiPD 策略可将产率由0.0215 g/(ml·p)提高到0.0280 g/(ml·p)，即产率提高了30.23%。总体来说，本文提出的EC-BiPD 策略优于传统SMB工艺和PD策略。

表4 不同策略间的性能参数对比Table 4 Comparison of performance parameters between different strategies

4 结 论

为提高模拟移动床分离过程的产率，本文提出一种带额外色谱柱的双部分丢弃策略。在该策略中，通过增大进料流量的方式来提高产率，新的工艺点不是传统地选取在完全分离区域内部，而是选取在纯提取产品和非纯提余产品区域。研究了该区域内的工艺点对模拟移动床所得产品纯度和回收率的影响，然后确定了最终的新工艺点。

根据积分纯度的概念，模拟移动床只收集在每个切换周期前期满足纯度要求的提余产品，而把后期中部分含杂质的提余产品暂时丢弃并收集在一个缓冲罐中。研究了提余产品的不同积分纯度阈值对其回收率的影响，得出提余产品积分纯度阈值的小幅提高会造成其回收率的大幅下降。在综合考虑提余产品的纯度和回收率这两个性能参数下，确定了所需的提余产品的积分纯度阈值。

缓冲罐中收集到的提余产品被作为循环进料通入到一个特定规格的额外色谱柱中，并研究了在该柱出口处两额外产品积分纯度的变化。通过设置额外产品的积分纯度阈值，以计算额外产品B 的收集截止时间和额外产品A 的收集开始时间，并把其余时间内的额外产品永久丢弃。本文还研究了两额外产品的积分纯度阈值对总产品性能参数的影响，结果表明随着额外产品A 积分纯度阈值的增加，产品A 的纯度始终高于98.00%且最大回收率为91.98%；额外产品B 的积分纯度阈值高于96.40%时，产品B的纯度才能达到98.00%。

本文最后对比了EC-BiPD 策略、传统SMB 工艺和PD 策略，结果表明EC-BiPD 策略可以在满足产品纯度的要求下，以较高的回收率利用进料。最重要的是，EC-BiPD 策略可将传统SMB 工艺的产率提高30.23%，在很大程度上解决工业生产过程中对原料需求量日益增加的问题。因此，本文提出的ECBiPD 策略切实可行且优于传统SMB 工艺和PD策略。