基于流量振荡的窄矩形通道内临界热通量机理模型

闫美月，邓坚，潘良明，马在勇，李想，邓杰文，何清澈

（1 重庆大学低品位能源利用技术及系统教育部重点实验室，重庆 400044； 2 中国核动力研究设计院反应堆系统设计技术重点实验室，四川 成都 610041）

引 言

作为反应堆三大热工设计准则之一，临界热通量(CHF)对设备经济性和安全性极其重要[1-3]，而流量振荡会导致沸腾危机在相对较小的热通量时发生，此时的临界热通量称为PM-CHF[4-6]。

流量振荡的发生会造成设备稳定运行范围减小，因此有学者尝试不同方法来消除流量振荡：Qu等[7]和Lin等[8]发现增加入口节流元件可以消除流量振荡。Fan 等[9]则发现增加入口节流元件只能在质量流速大于550 kg/(m2·s)时降低微通道的流量振荡。Maulbetsch[10]认为节流方法仅适用于短通道，对于L/D＞150 的长加热通道来说，并不能消除流量波动和沸腾危机的早发。Kaya等[11]实验发现即使增大入口节流仍然可观察到微通道的PM-CHF。

另有学者观察了流量振荡发生时的回路特性。Haas 等[12]在环形管道中发现流动不稳定时的PMCHF 为稳定CHF 的60%。Stoddard 等[13]指出在水平环形管道中增加热通量、提高入口水温以及降低压力都会促使流动不稳定性提前。Lee 等[14]发现流量漂移和流量振荡都可能会引起沸腾危机早发，且在PM-CHF发生时，通道内流型通常表现为弹状流-搅混流。Zhao等[15]的研究结果表明在低压竖直圆管中流量波动周期在1～11 s之间。

Ghione 等[16]指出在窄矩形通道中流动不稳定性的起始点与常规通道不同。而随着窄缝宽度的减小，流动不稳定性的脉动更强烈[17]。Sudo等[18]在常压窄矩形通道内双向流动的沸腾临界实验中发现，在向下流动的低质量流速区会发生由于流动反转导致的沸腾临界。于德海[19]和何海沙[20]将低压下窄矩形通道内的PM-CHF分成低质量流速和高质量流速两种情况，转换点约为400 kg/(m2·s)。盛程等[21]在自然循环饱和沸腾的条件下发现流量波动会造成流型不稳定，甚至会造成流动停滞。

目前关于PM-CHF 的研究并没有涉及窄矩形通道中的沸腾危机触发机理。特别是在截面具有较大长宽比窄矩形通道中，由于通道阻力更大，流动不稳定的脉动更强，气泡行为与其他通道存在很大不同[22-24]，更容易造成气泡堵塞。因此本文对矩形窄缝通道内PM-CHF 触发机理展开了可视化实验研究，分析窄矩形通道内气泡行为及流型演变过程，并从流量振荡的角度进行理论分析与推导，建立窄矩形通道中流量振荡条件下PM-CHF 预测模型。

1 窄矩形通道沸腾临界实验

1.1 实验回路

为了准确获得窄矩形通道在不同工况下的CHF 值，本文设计并搭建了如图1 所示的实验回路，回路主要包括主回路、冷却回路、水补充回路等。

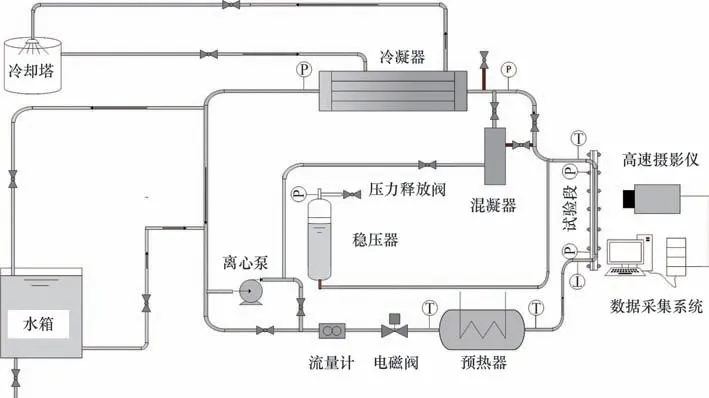
图1 实验回路示意图Fig.1 Schematic diagram of experimental loop

单相液体流入预热器，通过预热器和冷却回路配合，保证实验段的入口温度。主回路由管路系统、主要部件、测量系统和可视化实验段组成。可视化实验段如图2 所示，为了观察加热通道内的气泡行为和沸腾临界情况，通道设计为单面加热，高速摄影仪(Revealer X113)从宽边记录通道内气泡行为，拍摄帧率和拍摄面积分别为4300 帧/秒和60 mm×60 mm。

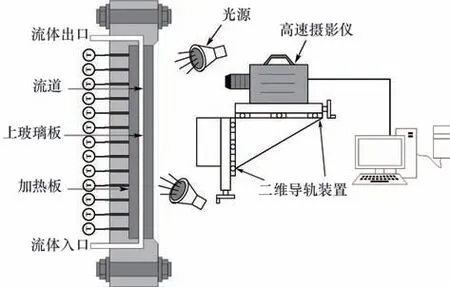
图2 可视化部分示意图Fig.2 Schematic diagram of visualization part

为了准确监测加热壁的温度变化，31 根T 型热电偶从不同位置进行温度读取。由于沸腾危机主要发生在靠近实验段出口的位置，为了及时反映沸腾危机发生时温度的突然升高并保护实验段，大部分热电偶被安排在靠近通道出口的位置。热电偶的测点分布如图3所示。

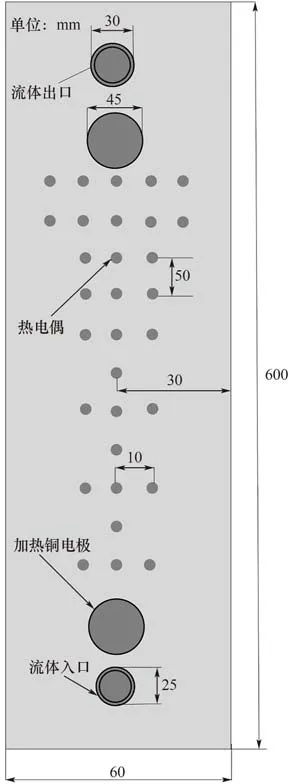
图3 热电偶布置图Fig.3 Schematic diagram of thermocouple locations

1.2 参数范围

实验的参数工况如表1所示。

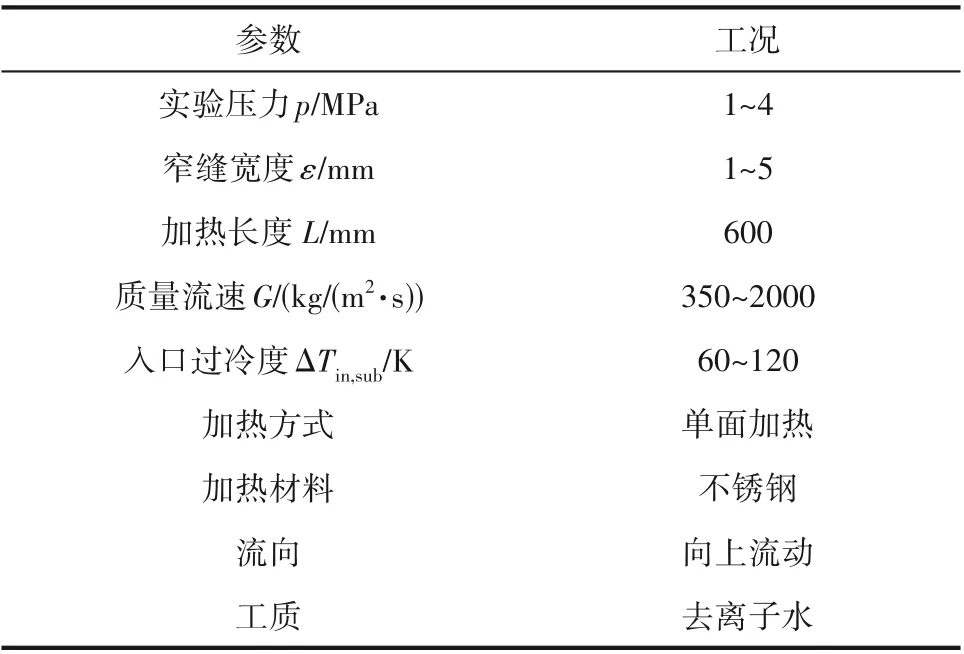
表1 实验参数工况Table 1 Range of experimental parameters

2 结果与讨论

2.1 质量流速对CHF的影响

图4示出了窄矩形通道中CHF随质量流速的变化情况。可以看出，随着质量流速的增加，CHF 几乎线性增加：一方面，随着质量流速的增加，用于加热流体的能量必然增加；另一方面，流体速度的增加使气泡脱离频率增加，加热壁面上气泡不容易聚集，增加通道内气泡的数量。质量流速较小时容易发生流动不稳定，回路中流量存在较大波动，流量波谷时容易发生沸腾危机；而随着质量流速的增加，流动惯性力增加，稳定性提高，相对于有流量波动波谷存在的流动不稳定工况，更不容易发生沸腾危机。因此在工况范围内，质量流速的增加可以提高CHF。

图4中

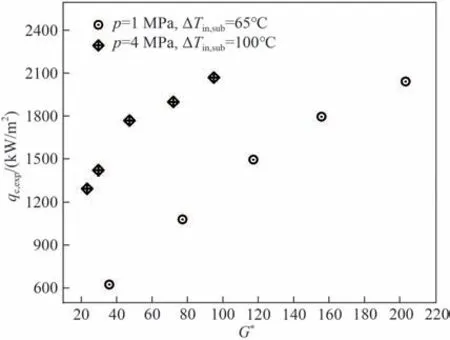
图4 质量流速对CHF影响Fig.4 The effect of mass flux on CHF

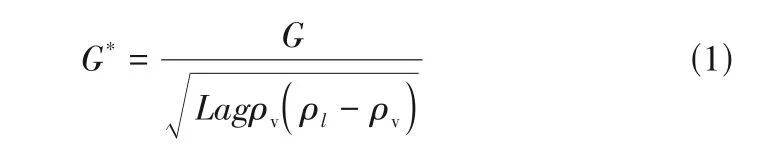
2.2 流量振荡对CHF的影响

当流量振荡，并接近沸腾危机时，通道中流型变化如图5所示。

从图5 可看出，流动不稳定性发生时弹状流和搅混流交替出现：0～50 ms 为弹状流，50～100 ms 为搅混流，从100 ms 又开始搅混流向弹状流的转变，因此由流量振荡引起的PM-CHF 主要发生在弹状流-搅混流区域，且流量振荡周期大约为0.1 s。对应回路流量波动和加热壁面温度变化如图6 所示，加热壁面温度以最靠近出口处的31 号热电偶温度为代表，其余热电偶具有相同变化趋势。

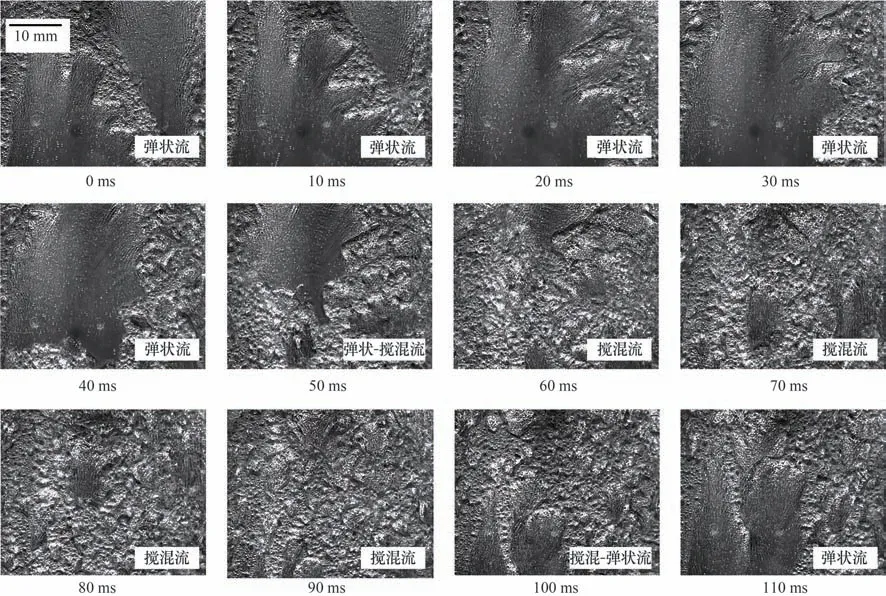
图5 流动不稳定性条件下CHF发生时流型变化Fig.5 The variation of flow pattern when CHF occurs under conditions of flow instability

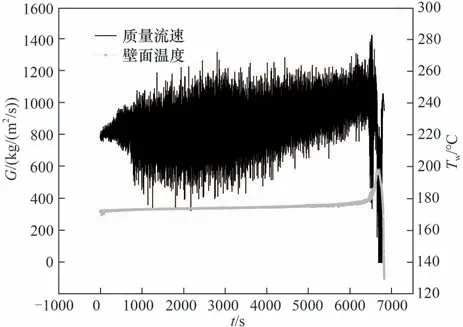
图6 流量振荡条件下CHF发生时流量和温度变化Fig.6 The variation of mass flux and temperature when CHF occurs under condition of flow oscillation

随着热通量增加，壁面沸腾更剧烈，含汽量升高，通道阻力增加，回路驱动力相对减小，气相和液相的同向运动减弱，液体对原气泡位置的相向补充运动更为显著；此时窄矩形通道中的边角效应和二次流也相对显著，因此通道中此时为搅混流，回路流量减小。随着时间的发展，气泡流出加热段，同时由于流速较小，液体补充和边角效应造成的二次流这种无序运动逐渐减弱，通道中阻力减小，系统驱动力逐渐加强，气相与液相的同向运动趋势增加，气泡在接近流道出口处产生大气泡弹，通道内流型转变为弹状流，驱动压头增加，流量增加；如此循环，导致回路流量处于一种波动形式。

当热通量较高时，加热壁面生成气泡频率及脱离速度增加，通道内气泡量增加，通道内二次流及两相的相对运动会使得通道阻力增加；当热通量继续增加并达到某值时，阻力的增加会使回路驱动力和回路流量减小到一定值，气相和液相的同向运动较弱，相向运动增强，同时由于气泡脱离频率和脱离速度很快，气体的扰动会使得液体无法补充到干涸点，会造成壁面温度升高而发生沸腾危机。

2.3 CHF模型

2.3.1 现有CHF 模型 现有的基于气液界面不稳定性建立的CHF预测模型如表2所示。

表2 不稳定性模型Table2 Instability models

根据Taylor不稳定性建立的CHF预测模型主要应用在池式沸腾中。目前有许多学者建立了过冷流动沸腾下CHF 机理模型，其中微液层蒸干模型得到了多数学者的认可[7-8]，微液层蒸干模型认为，气泡弹与加热面之间存在微液层，当微液层中的蒸发速率大于液体润湿壁面的速率时CHF 发生。而且微液层蒸干模型认为气泡弹的大小是根据Helmholtz流动不稳定性确定的，可以将CHF与流动不稳定性联系起来，因此本文将实验值与根据Helmholtz不稳定性建立的CHF预测模型进行比较，结果如图7所示。

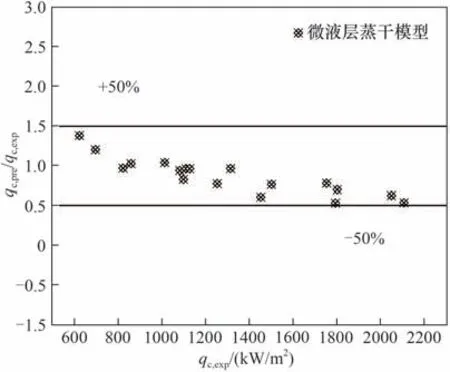
图7 微液层蒸干模型预测值与本实验值的对比情况Fig.7 The comparison between the prediction of sublayerdryout model and the experimental value

2.3.2 新CHF 模型 假设：(1)由于CHF 发生时，气泡尺寸几乎与通道宽度相当，因此气液状态在同一水平高度处一致，表现为沿流动方向(x)和垂直于加热壁面方向(z)上的二维流动；(2)忽略流体的压缩性和黏性。

则无论液相还是气相，相应的控制方程为：连续性方程

当气泡从加热壁面脱离时，周围液体进入补充并对加热壁面进行冷却。在高热通量下，气泡产生和脱离速度增加；当热通量达到某值时，气泡从加热壁面脱离速度足够快，将会阻碍液体的补充，从而导致加热壁面温度上升，发生CHF。而对于竖直流动来说，气泡脱离加热壁面和液体的补充运动可以看成是垂直于加热壁面方向上的相对运动，而重力对垂直于加热壁面方向上的运动没有影响，因此式(24)中右侧第二项不是影响流动不稳定性的因素，因此对于竖直流动的临界速度

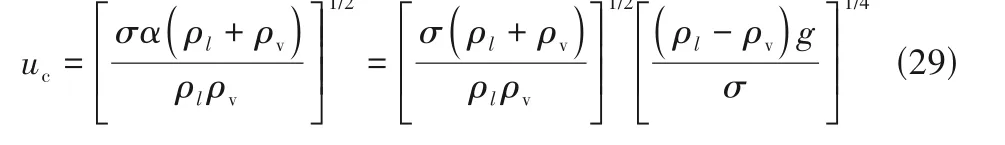
本文假设汽化核心在加热壁面上是正方形分布，相邻汽化核心之间的距离相等[29]；而且在热通量较高甚至临近CHF 时，加热壁面过热度已经很高，汽化核心数量已经达到极限，因此再进一步增加热通量，加热壁面上汽化核心数量并不会较大变化，而只是增加气泡脱离频率和脱离速度[30]。

如图8所示，当发生CHF时，气液交界面表现为正弦波形(在弹状流时，由于大气泡的产生，气液界面提升，相当于波动的波峰，搅混流对应波动的波谷，波峰和波谷所占时间相同)，因此对于每个波动周期在加热壁面上主要可以分为波峰和波谷两个区域，每个区域对应的热通量如下。

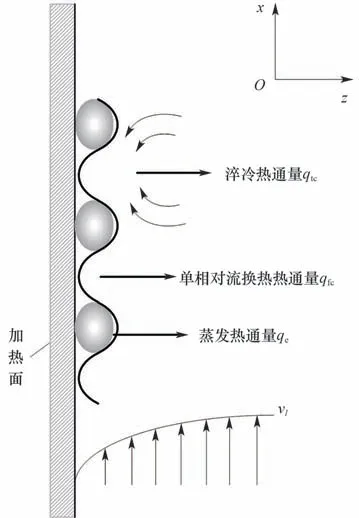
图8 CHF发生时气泡行为及热通量分布示意图Fig.8 The schematic diagram of bubble behaviors and heatflux distribution when CHF occurs

产生气泡的核化区：由于气泡的产生对应周期的波峰，而此处基本被气泡覆盖，主要为蒸发热通量；核化点的间隙：气液搅混时对应波动的波谷，当气泡脱离加热壁面时会有冷流体补充进入气泡原来的位置，此时对应加热壁面的热通量为淬冷热通量，以及加热壁面和流体之间的单相对流换热热通量。

将图8 与图5 中的可视化结果对应，在弹状流时，由于大气泡的产生，气液界面提升，相当于图8中的波峰，因此在波峰处主要对应蒸发热通量；而在搅混流时，气液搅混，对应冷流体补充原气泡所在位置的淬冷换热热通量以及与液相直接接触的单相对流换热热通量。根据高速摄影仪拍摄的图像，波峰和波谷出现的时间间隔相同，因此认为对于每个周期来说，波峰和波谷所占面积相同。而且波峰处主要对应蒸发热通量，波谷主要对应淬冷热通量和单相对流换热热通量，因此对于每个周期，每个热通量仅占一半的波动面积或波动时间的一半，因此当关注整个周期下的临界热通量时，CHF计算式为：

所建模型与实验值的比较结果如图9 所示，可以看到模型的预测值与实验结果吻合较好。

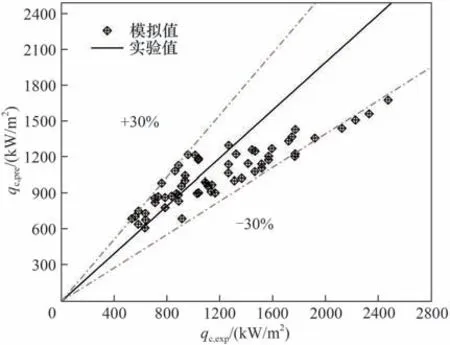
图9 模型计算值与实验值对比Fig.9 The comparison of the predicted values and experimental values

表3 汽化核心密度预测关系式Table 3 Correlations of nucleate site density

3 结 论

(1)本文通过可视化实验，观察到在窄矩形通道中临近CHF 发生时，流量波动会造成流动不稳定，其表现为弹状流-搅混流。

(2)CHF随质量流速增加而增加，且在窄矩形通道中会发生由流量振荡造成的PM-CHF，流量振荡周期约为0.1 s。

(3)基于流量振荡以及窄矩形通道内气泡特性，建立了新的窄矩形通道内PM-CHF 机理模型。该模型可将与实验值的对比预测误差控制在30%以内，相比于使用微液层蒸干模型描述时50%的对比误差有了较大提升。

符 号 说 明

g——重力加速度，m/s2

L——矩形通道加热长度，m

r——半径，m

δ——气相厚度，m

ρ——密度，kg/m3

σ——表面张力，N/m2

下角标

c——临界值

e——蒸发

exp——实验值

fc——对流

in——入口

l——液相

pre——预测值

sub——过冷

tc——瞬态导热

v——气相

w——壁面