基于ANFIS的多因素PSO_BP_PID算法在列车防冒进中的研究
姜俊彤 李 鸿 苏 醒
(长沙理工大学电气与信息工程学院 湖南 长沙 410114)
0 引 言
长久以来,列车实验线防超速都是基于单纯线性化距离-速度的控制策略与司机经验相结合进行人工防护,但实际上列车运行过程十分复杂,具有很多不确定因素与离散性[1-2]。由于轨道交通安全运行问题日渐被我国重视,针对传统的列车传递函数进行控制难以满足现实需求。
近年来,随着列车精确定位技术的研究日渐成熟[3-4],基于车载列车设备上的安全防护控制算法的研究也日益深入:林颖等[5]针对CBTC车载设备提出安全制动曲线模型,董海鹰等[6]提出将模糊神经网络应用于高速列车ATP上,并利用预测控制对其进行基于速度-距离的一次制动,但预测控制自我调整较为缓慢的缺点难以避免;柏卓彤等[7]提出基于速度距离表的安全制动曲线,对列车安全行驶提出更高的要求;谭莉等[8]对ATP曲线制定的步长上进行研究,但ATP防护曲线不等同于列车期望输出序列,并未对目标序列提出研究;姜俊彤等[9]提出基于ANFIS模型在防冒进系统上直接进行制动控制,但在理论分析上可看出,随着初始制动速度的增加,在众多列车影响因素作用下,其误差也在显著增加。上述算法对于使用ANFIS模型在列车行驶模型的可行性上进行了研究,但针对列车行驶的多因素需求及需求下的速度控制器的研究则甚少。本文在文献[10-11]的基础上,建立基于ANFIS的列车离散化模型,并针对安全防护曲线下的目标输出序列进行优化,并设计基于PSO_BP_PID算法的速度控制器,从而达到保证列车在多因素需求下行驶的要求。
现有的防冒进系统控制策略控制方法主要有两种[12]:第一种为触发防护曲线即采取紧急或满常单一挡位制动;第二种为触发防护曲线之后以PID对其进行变挡控制。在列车运行线路加长且线路运行条件复杂多变的情况下,仅以防护曲线采取单一挡位制动明显是不符合需求的。而PID控制虽然具有算法的局限性,在模型切换情况下的速度跟踪存在局部跟踪切换频繁的问题,造成了运行冲击率指标较大等结果。而冲击率影响着乘客乘坐列车的舒适度,频繁地切换在一定程度上也加快了列车设备的损坏。而对于耗能方面,由于加速度频繁地切换列车挡位,控制下的列车耗能也无法有效解决。尽管有上述一系列问题的存在,但由于PID控制算法理论成熟、容易应用,并且以人工驾驶为主的情况下对控制精度要求不高的情况存在,其仍然是当前列车防冒进系统中一个很好的选择。
1 防护曲线建模
本文以理论制动防护曲线行驶数据为对象,以相同时间区段积分分解的方式通过列车加速度与速度传感器以及列车距离定位装置采集到的数据建立最优限速目标模型。以从开始制动到结束制动的以0.5 s为时间区段的{t0,t1,t2,…,tn}中采集到的速度{v1,v2,…,vn}、距离安全停车点的距离{d1,d2,…,dn}、{a1,a2,…,an}建立目标模型。
在目标模型中的速度信号是通过列车车轮速度传感器采集,由于车轮存在着空转等干扰传感器信号准确度的情况,采用小波算法阈值去噪法作为判断噪声的依据从而对速度信号进行降噪,去除速度数据集的高斯白噪声,算法流程如图2所示。

图1 去噪算法流程
其中母小波采用DB4小波,对其进行6层分解,阈值处理函数选取rigrsure阈值与软阈值去噪法,其公式如下:
(1)
f(k)=(sort(|s|))2k=0,1,…,N-1
(2)
(3)

(4)
(5)

(6)

提取基于时间序列的经过小波去噪后的速度信号{vφ0,vφ2,…,vφn}与目标距离{d1,d2,…,dn},由于高斯模型有着对任何函数逼近的效果,故对速度与目标距离的关系根据拟合效果选用四阶高斯变换以95%置信度为置信区间对数据集进行处理,得到速度与制动距离拟合公式如下:
d_car=a1×exp(-((v_car-b1)/c1)2)+
a2×exp(-((v_car-b2)/c2)2)+
a3×exp(-((v_car-b3)/c3)2)+
a4×exp(-((v_car-b4)/c4)2)
(7)
式中:d_car为制动距离;v_car为列车速度;ai为权重系数;bi为均值系数;ci为方差系数。
2 多因素目标序列
由于获取到的基于时间序列的速度、加速度、目标距离数据仅是对于安全停车的要求,并未将列车运行的舒适度、节能性因素进行考虑。故本文基于第1节速度-距离曲线作为安全停车的参考,采用粒子群算法将多因素评价指标作为适应度函数对目标曲线进行优化。
2.1 改进的粒子群算法
粒子多维位置矩阵取决于数据的解,每个粒子的位置都代表着一组对于问题的解值,即单个粒子位置矩阵的列数为c。当样本数据是多维度d的情况下,单个粒子位置矩阵维度为c×d。若e为粒子群的种群数量,则粒子群矩阵维度将为c×d×e。在此情况下单个粒子群的矩阵可表示为:
x(:,:,a)=[p11,p12,…,p1c;…;pd1,pd2,…,pdc]
a=0,1,2,…,e
(8)
式中:pij为第a个粒子群中第i个样本维度的第j个聚类中心。
适应度函数是能把粒子群优化的关键部分,对于粒子群算法学习的依据便是适应度函数的优劣。则本文的训练迭代目标函数公式为:
P_fitnessmin=w1fs+w2fe+w3fj
(9)
式中:fs为行车精确度指标;fe为平稳性指标;fj为节能型指标;w1、w2、w3分别为各自指标的权重系数,且满足w1+w2+w3=0。
在实际寻优过程中,各个粒子之间其实是相互独立的,每个粒子的学习效果是不尽相同的,若单纯以线性递减的方法而忽略粒子间的特性而对样本数据进行学习,将会使得部分适应度低的粒子丧失对整个族群学习的贡献。故本文将每个粒子的惯性因子独立起来,并对每个粒子的学习因子进行系数补偿,使其具有根据自身学习的速度动态调整惯性因子的能力,即:
vi(j+1)=wvi(j)+c1r1(pi(j)-xi(j))+
c2r2(pbest(j)-xi(j))
(10)
xi(j+1)=xi(j)+v(j+1)
(11)
(12)

(13)
式中:w为惯性因子;c1、c2为学习因子;r1、r2为0到1之间的随机数;vi(j)为第j次迭代第i个粒子的速度;xi(j)为第j次迭代第i个粒子的位置;pi(j)为第j次迭代第i个粒子的个体最优值;pbest(j)为第j次迭代之后整个粒子群的全局最优解;W0为整体的线性递减的学习因子;h为补偿系数,h∈[-0.5,0.5]。

2.2 评价指标的选择
由于对目标曲线的优化归根结底是对频域上的速度进行的,故每项指标的选定其实是关于速度选取的变量,因此本文构建以加速度为寻优变量的满足列车运行为要求的粒子群适应度函数。
2.2.1停车精确度指标
在每个寻优周期下,为保证列车在停车方面的精确度,制动距离与v-s曲线应尽可能相同,故本文对停车精确度指标定义如下:
v_car(t)=v_car(t-1)-(a×t)
(14)
Δs=(v_car(t)+v_car(t-1)×t)/2
s_car(t)=s_car(t-1)-Δs
fs(t)=|s_car(t)-d(v_car(t))|
(15)
式中:v_car(t)为t时刻的速度;a为t-1时刻寻优的加速度;Δs为距离的增量;s_car(t)为t时刻距离目标停车点的距离;fs(t)为停车精确度指标。
2.2.2行车平稳度指标
行车平稳度通常是以列车乘客对于加速度变化率的心理反应作为评价,当加速度变化率越慢,即行车越平稳,乘客的心理反应越舒适,故本文对于行车平稳度的指标如下:
fa=|a(t)-a(t-1)|
(16)
式中:a(t)为粒子群当前寻优的解;a(t-1)为上次循环粒子群最优解。
2.2.3节能性指标
列车运行的能耗与众多影响因素有关,比如列车上的设备、牵引制动时的机械、车轮的磨耗程度等。由于难以对不可避免因素进行控制,本文仅对列车行驶时的动力学模型进行分析,即技能型指标为:

(17)
式中:E为耗能;m为列车质量;at-1为t-1时刻的加速度;Δs为t时刻与t-1时刻间的速度增量。
而算法寻优过程中,vt-1为每次最优结果计算下的常量,故可得出E=f(a3)。即节能性指标归根结底与加速度本身的大小有关,则技能性指标为:fj=|a3|。
2.2.4限制性因素
由于粒子群算法是对整个求解空间进行寻优,难以避免会碰到不符合正常行驶条件却又指标优良的最优解。针对列车运行的现实条件对算法进行约束,当粒子群寻优解超过约束条件时,适应度函数取极大值。
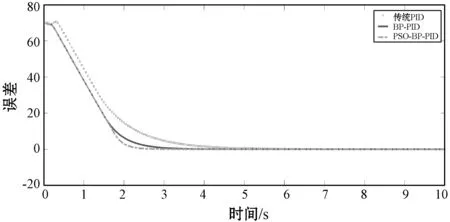
1) 安全性。在安全性指标考虑上,v_car s_car(t)-d(v_car(t))>0 (18) 2) 动力学限制性。在列车制动过程中,由于制动力的原因,加速度应与列车运行速度的方向相反,即寻优的解即x(i)≤0。根据各个参数的动力学模型与现实数据,城轨列车的最大减速度不该超过固定值,即x(i)≥-1.5。 若将列车在运行区间看作一个质点在多种作用力下进行运动,其力学模型可简化为下列公式: C=F-W-B (19) 式中:F为当前牵引工况下的牵引总力;W为线路运行条件下的总阻力;B为当前制动工况下制动总力。倘若由c来表示列车单位合力,则当机车处于制动状态时,机车的力学模型可以表示为: c=-w-βCb=-(w0+ij+βcb) (20) w0=a+bv+cv2 (21) 式中:βC为常用制动系数;b为机车单位动力制动力;单位阻力w由单位基本阻力w0和单位附加阻力组成[11]。线路的多种影响因素组成了列车的单位附加阻力,并且存在着时变性、非线性等特点,在实际的使用中难以理论化公式应用其中。因此,通常w0的使用将会采用大量实验综合得到的经验公式作为使用依据。 根据受力分析,可以计算加速度、速度等,计算加速度公式如下: (22) 式中:a为列车加速度,单位为m/s2;c为列车单位质量合力,单位为N/kN;γ回转质量系数,一般为0.06。 由3.1节受力分析可知列车的运行过程充满了非线性的特点,而控制模型对于PID算法的控制精确度具有十分重要的影响。基于对上述问题的考虑,本文采用ANFIS对于列车离散化方程进行建模。 可将列车非线性模型改写为: v(t)=F(v(t-1),a(t-d)) (23) 式中:v(t)与v(t-1)为t时刻的输出与输入量;d为输入量滞后时间,在理想运行状态下加速度的滞后时间为1;F(x)为经过优化后的模糊神经网络逼近的非线性离散函数。 模糊神经网络训练集采用离线训练的方式对923组历史数据集进行训练,并加入至模糊神经网络训练步骤。基于列车制动过程的离散性与非线性,考虑到高斯型隶属度函数对于复杂系统的良好逼近能力,故本文选用高斯型隶属度函数进行模糊神经网络的学习。以双输入网络最大化模糊规则数的原则,设定模糊聚类的分类数为9,进行样本集的模糊聚类训练。 模型结构如图2所示。 图2 模糊神经网络结构 图2为本文双输入、单输出神经网络模糊系统的结构示意图,它采用多层前向神经网络,每层完成一个特定的任务然后把信息传到下一层。通过T-S模糊模型的表达方式对列车离散化非线性模型进行表达。 对于列车制动这种非线性、时变系统而言,PID控制具有良好的稳态响应特性,而在动态响应特性上则难以达到列车行驶快速响应的要求。BP-PID具有对于系数自整定、动态响应良好的特点,但初始化的随机权重系数对于算法的控制效果与学习速率有所影响。故本文采用具有优化初始权重功能的PSO_BP_PID算法进行控制。 控制器由三部分组成,分别为优化后的预测序列、基于PSO_BP_PID的控制器、基于ANFIS的列车运行模型。速度控制器结构如图3所示。 图3 速度控制器结构 采用增量式PID的控制器算式为: (24) 式中:u(k)为系统第k时刻的输出;e(k)为系统第k时刻误差。 用于PID控制系统的神经网络结构如图4所示,设有n个输入节点、m个隐含层节点、k个输出节点。输入节点的选取与影响PID控制的状态变量有关,在此选为3。隐含层节点的选取暂时没有理论性的依据,一般不小于m+n-1,隐含层的节点越多对于输入与输出的描述更为精确,但过多的隐含层选择将会影响系统学习的效率,在满足精度的前提下选取隐含层节点数为5。神经网络的输出为PID的控制量,在此选为3个节点,分别对应着Ki、Kd、KP。BP神经网络的输入为: xi(k)=e(k+1-i) (25) 从而可得隐含层的输入输出为: (26) (27) (28) (29) 从而可得: (30) 可得神经网络输出层的计算式: (31) 同理可得隐含层输出为: (32) 式中:g′(x)=g(x)[1-g(x)];f′(x)=1-f2(x)。 图4 BP神经网络结构 针对列车超速防护需要时刻满足复杂运行条件的要求,将模糊神经网络应用于列车运行模型中,通过其算法能够逼近任意非线性模型的优势,训练结果作为列车运行离散化模型。对基于时间序列的传感器数据进行小波去噪,并对其进行高斯线性拟合从而得到防护曲线的关系式。并基于防护曲线,通过改进型粒子群算法进行寻优得到基于多因素考虑的目标速度序列,将其作为基于PSO_BP_PID的速度控制器的目标输出。具体算法流程如下: 步骤1通过小波算法离线处理基于时间序列的防护曲线传感器数据,并通过高斯线性拟合得到防护曲线结果。 步骤2初始化粒子群规模与属性,建立以fs准确度、fj节能性、fa舒适度多指标的适应度函数,并通过改进型粒子群算法迭代学习并更新初始化属性,从而得到基于控制周期的目标输出序列。 步骤5采用阶跃信号对神经网络的权重进行学习,控制器趋于稳定之后将目标序列作为其输出期望,将ANFIS的离散化方程作为其运行模型进行控制。当实际输出与期望输出之间产生误差时,速度控制器将多步误差作为输入,通过神经网络对Kp、Ki、Kd三个整定系数进行输出,达到调节速度与期望速度一致的目的。 本文通过MATLAB实验方法,对所建立的基于ANFIS的多因素PSO-BP-PID速度控制器进行仿真分析。实验条件以中车株机试运线道路数据为例,实验列车行驶数据以两台SS3型电力机车头为相反方向动力来源并且不挂载货运车厢的行驶实验常用结构为例,以70 km/h为运行最大速度,并通过多项指标对比其控制策略优势。 采用最小方差估计对规则后件进行辨识,获得规则后件参数。结合反向传播法和梯度下降法对ANFIS模型前/后参数进行优化调整,训练误差见图5。 图5 ANFIS误差训练 写成覆盖vin∈[0,70]的模糊子集高斯型隶属函数表达式: 通用可以写成覆盖ain∈[0,1.2]的模糊子集高斯型隶属函数表达式: 归纳出列车离散化运动方程由以下9个模型组成: R1:vout1=vin+0.024 35ain-0.003 964 R2:vout2=0.998 9vin-0.015 21ain-0.012 63 R3:vout3=0.997 5vin-0.042ain+0.003 189 R4:vout4=0.999 5vin-0.133 8ain+0.017 14 R5:vout5=0.999 8vin-0.071 33ain+0.023 28 R6:vout6=0.998 6vin-0.056 05ain+0.057 R7:vout7=0.999 7vin-0.017 67ain+0.022 34 R8:vout8=vin-0.034 26ain-0.010 53 R9:vout9=0.998 5vin-0.050 74ain-0.107 3 想要达到对被控系统与实际相同的控制效果,其运动模型的建立是关键。而由图5可看出通过ANFIS学习之后的模糊表达式对于列车离散化运行模型有良好的表达效果,其均方根误差稳定在0.008 9左右,满足列控系统的精度要求,与列车的实际运行数据有着优良的拟合度。 为验证改进型粒子群对于目标序列的优化程度,对其进行0.5 s为迭代周期的算法初步仿真并对其性能指标进行计算,仿真结果如图6所示。 图6 粒子群优化结果 运行计算指标如表1所示。 表1 评价指标 可以看出,通过改进型粒子群对于防护曲线进行算法优化,得到的目标输出序列与理论防护曲线的拟合程度非常高。但通过指标计算可以看出,本文基于多因素考虑的目标序列,在距离指标上与多因素相比有所优势,但同时在舒适度指标上降低了13.2%,而在耗能指标上降低了7.1%左右,从而在综合性指标上相比多因素指标降低了4.6%。故通过初步仿真可以看出,本文对于目标输出序列在保证精确度的情况下,对列车行驶的多因素进行考虑的优化方法是行之有效的。 若在列车真实运行线路下采用神经网络进行训练,训练过程中造成的安全问题难以解决。故神经网络的训练采取以模拟控制系统给与阶跃信号在线训练的方式,即以控制系统反馈的e(k)、e(k-1)、e(k-2)作为输入,以三个参数即Kp、Ki、Kp为输出进行训练直至控制系统达到稳定。为保证神经网络在控制系统中训练的样本数据集的充足性,设定整个控制过程为10 s,即在以0.05 s为控制周期的控制过程而言数据样本有200组数据集。 为验证本文算法对于传统的PID算法与BP-PID算法的优化,并在考虑列车实际运行安全性的情况下,规定在超调量为0的参数下对模糊神经网络训练下的列车多模型进行阶跃信号仿真,并计算其动态与静态性能指标,仿真结果如图7、图8所示。 图7 阶跃信号误差 图8 阶跃信号跟踪 动静态性能指标如表2所示。 表2 动静态性能指标 可以看出,三个算法在静态指标下都十分优良,在∞的周期上传统PID的静态误差在0.001 58左右,而PSO_BP_PID与BP_PID收敛于0.000 2左右。由于目标输出值设定较大,故采用进入0.02%的误差实际为调节时间。BP_PID相比传统PID在动态性能上优化效果十分明显,上升时间指标减少了0.55 s,调节时间指标减少2.3 s。而PSO_BP_PID相比BP_PID算法在动态性能上有所改进,这得益于相比随机初始权重,通过粒子群对于初始权重进行选择有效提高了BP-PID算法的学习速率。 将基于ANFIS的训练模型作为列车离散化运行模型,基于粒子群优化的多因素目标序列作为列车设定输出,以0.05 s为控制周期,以70 km/h为初始速度,以距离安全停车点314.981 2 m作为初始化路程,对其进行防冒进运行仿真并对性能指标进行计算,计算结果如表3所示。由于通过阶跃信号学习之后的PSO_BP_PID与BP_PID算法在控制效果上差异甚小,故仿真仅对本文算法与PID算法进行比较,仿真结果如图9-图14所示。 表3 算法性能指标 图9 速度总体跟踪 图10 速度局部跟踪 图11 速度误差跟踪 图12 加速度跟踪 图13 加速度增量跟踪 图14 耗能跟踪 将以0.05 s为控制周期与0.5 s为控制周期的仿真结果进行对比,弱化周期步数对于路程误差指标计算的影响,从仿真结果与性能指标可以看出,通过细化控制周期的方式能够有效提高列车行驶时的综合性能,细化控制周期后的舒适度仅为上文指标的25.2%,耗能指标仅为上文指标的19.3%。说明本文算法能够在保证列车安全行驶的精确度的前提下,有效提高运行的舒适度,降低了行驶耗能,达到了列车考虑多因素运行的需求。 以我国试运线上列车防冒进的控制需求出发,针对列车制动过程高度非线性、影响因素众多、强耦合性等特点,建立基于ANFIS的列车制动离散化方程,并通过基于多因素考虑的改进型粒子群算法建立基于防护曲线的目标输出序列,并针对列车速度控制器进行设计。仿真结果表明本文基于ANFIS建立的多因素PSO_BP_PID算法在保证列车安全行驶的情况下具有行驶舒适度高、耗能低的优点。3 基于ANFIS的列车运动模型
3.1 受力分析
3.2 列车运动离散化方程建模

4 列车速度控制器设计
4.1 速度控制器结构

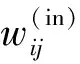


4.2 算法流程


5 仿真实验与结果分析












6 结 语

