DC系列汽车板常用流动应力模型的研究

张东凯，张龙柱，李晓广，余亚克，穆康奇

(河钢集团邯钢公司 用户技术研究中心，河北 邯郸 056015)

汽车作为大众消费品，其60%～70%的零部件制造采用冲压成形工艺[1]。传统冲压成形工艺设计主要依靠现场试错方式来进行，这无疑增加了生产成本和周期。随着计算机技术的发展，通过有限元方法对冲压成形进行模拟仿真，可以指导冲压工艺，从而减少试制次数，提高生产效率。流动应力曲线作为冲压成形仿真的一个关键输入参数，其准确性直接影响仿真精度。目前流动应力模型的研究有很多，包括理论与试验研究[2-7]。李宏烨[8]研究了不同流动应力模型对C15E(5 mm)不锈钢在小应变(均匀应变)范围内的拟合精度。崔伟强[9]基于屈服点至颈缩点间的真应力-塑性应变曲线，通过单向拉伸仿真对比分析了8种不同硬化准则对该材料的适用性，确定了Swift-Hockett-Sherby组合模型的加权系数。H.J.KLEEMOLA等[10]研究了Ludwik、Hollomon、Swift和Voce模型对退火铜流动应力曲线的适用性，预测了均匀应变值，发现Hollomon模型在对数坐标系中线性相关系数很高，但预测的均匀应变误差却很大。程超[11]采用AUTOFORM软件中常用的4种流动应力模型对DC04E+Z、DC56D+Z和HX220YD+Z的试验数据进行拟合，从均方差角度分析了拟合误差，结果发现Swift-Hockett-Sherby组合模型拟合效果最好。董伊康[12]采用Ludwik、Swift、Hockett-Sherby、Voce、Swift-Hockett-Sherby、Swift-Voce流动应力模型对DX56D+Z、HC220BD+Z、HC420LA、HC420/780DP4汽车钢板小应变范围内的流动应力试验曲线进行拟合，并从相关系数角度分析拟合精度。Sebastian Dziallach[13]采用激光光学测量设备对DX54、DP600、TRIP700进行了液压胀形试验，并通过拟合单向拉伸试验曲线，分析了不同流动应力模型在大应变范围预测精度。李宏烨[14]基于中厚板材料的拉伸曲线，研究了8种流动应力模型的物理意义，从相关系数及均方差两个方面分析了拟合精度，并提出了利用轧制-拉伸实验方案得出大应变流动应力曲线。刘国承[15]基于Swift和Voce模型建立Swift-Voce模型，从相关系数、均方根两个方面对汽车板的流动应力曲线进行拟合分析，结果发现Swift-Voce模型可以有效预测DX54深冲钢在大应变范围内的流动应力。

目前对流动应力模型的研究多局限于小应变分析，钢种跨代大，缺乏对DC全系列深冲钢(简称DC系列)的研究，包括冷轧和镀锌，且对该系列钢种大应变分析的少。而DC系列深冲钢广泛应用于汽车车门、前后盖、顶盖等内外板及加强件中，使用量大，因此选取了DC01、DC03、DC04、DC05、DC06、DX53D+Z、DX54D+Z、DX56D+Z及DX57D+Z共9种DC系列汽车板和Combined Swift-Hockett-Sherby(Combined S-H)、Ghosh、Swift、Hockett-Sherby、Voce共五种常用流动应力模型。将这些模型拟合DC系列汽车板均匀应变范围内的拉伸曲线，分析了拟合精度。之后分析了DC系列汽车板流动应力模型在大应变范围内的差异性和规律性。最后以DX54[13]单向拉伸曲线为拟合对象，结合DX54液压胀形试验曲线,分析了常用五种流动应力模型对DX54深冲钢大应变范围的适用性。

1 常用流动应力曲线模型

目前流动应力模型很多，如Hollomon、Ludwik、Swift、Ghosh、Hockett-Sherby、Combined S-H、Voce、Voce+Voce、Voce++、ThyssenKruppTEM等模型，但是在成形仿真软件中，常用的有Swift模型、Ghosh模型、Hockett-Sherby模型、Combined S-H模型、Voce模型，其表达式如下：

符号说明：σ为真应力，εpl为真塑性应变，σs为真屈服强度(等于实验中的屈服强度)，exp[X]=eX。

Swift模型为非饱和模型，无初值：

σ=C(εpl+ε0)p

(1)

式中：C、p为大于零的拟合参数，ε0为屈服强度对应的应变。

Ghosh模型为非饱和模型，无初值：

σ=C(εpl+ε0)p-D

(2)

式中：C、D、ε0、p为大于零的拟合参数。

Hockett-Sherby模型为饱和模型，即随着塑性应变增大，真应力趋于定值，初始点为屈服强度点：

(3)

式中：σsat、a、p为大于零的拟合参数。

Combined S-H模型是Swift模型和Hockett-Sherby模型的组合，它引入权重系数α，通过调整权重系数来优化拟合曲线：

σ=(1-α)C(εpl+ε0)p2

(4)

式中：C、ε0、p2、εsat、a、p3、α为大于零的拟合参数。

Voce模型为饱和模型，初始点为屈服强度点:

σ=σs+A[1-exp(-mεpl)]

(5)

式中：A、m为大于零的拟合参数。

2 均匀应变范围内的拟合分析

对DC01、DC03、DC04、DC05、DC06、DX53D+Z(53D)、DX54D+Z(54D)、DX56D+Z(56D)及DX57D+Z(56D)共9种牌号(以下简称DC系列)进行单向拉伸测试，测量结果见表1，真应力真应变曲线见图2。

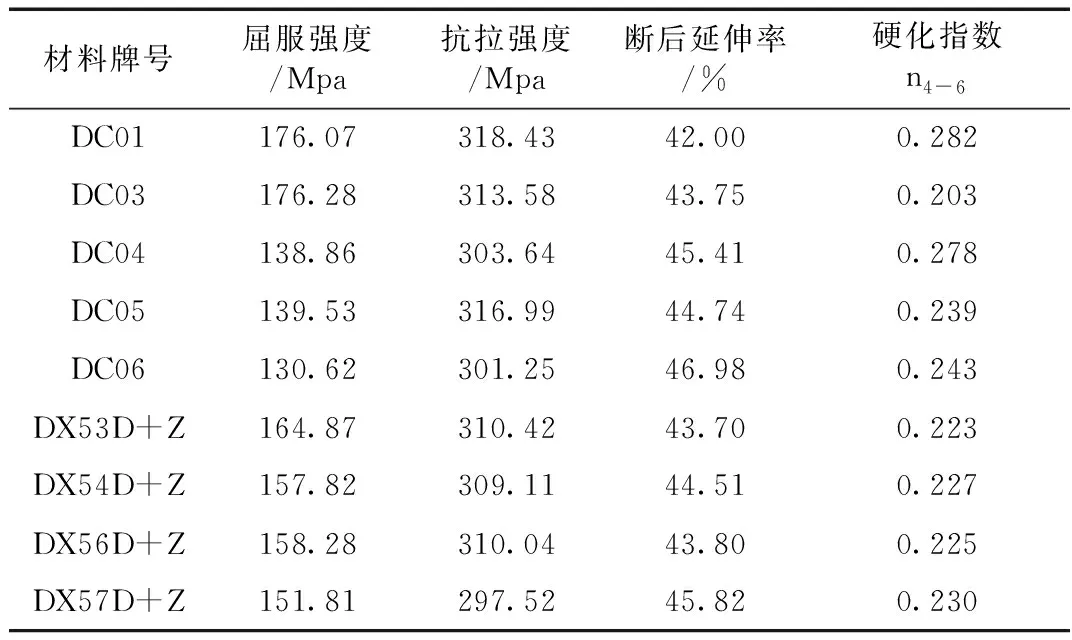
表1 轧制方向拉伸试验测量结果

图1 不同牌号材料的拉伸曲线

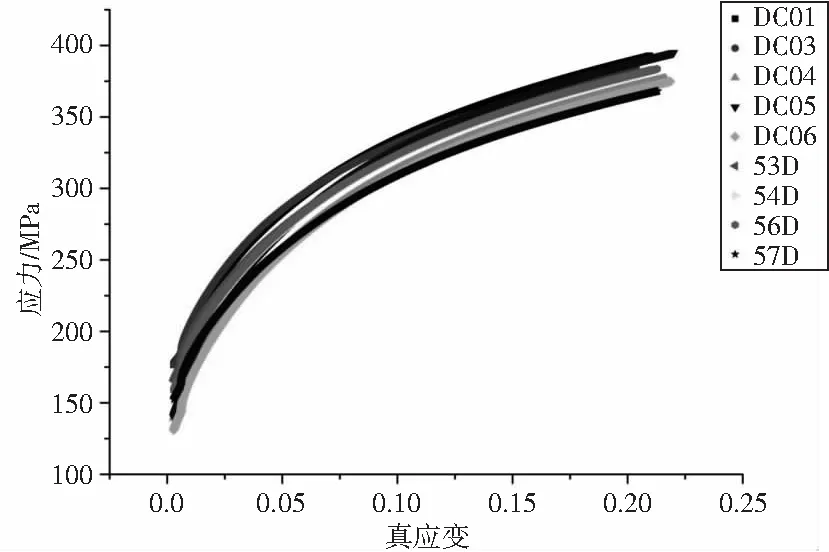
图2 真应力塑性应变曲线

2.1 曲线拟合

采用Swift、Ghosh、Hockett-Sherby、Combined S-H、Voce共5种常用流动应力模型对图2曲线拟合见图3。

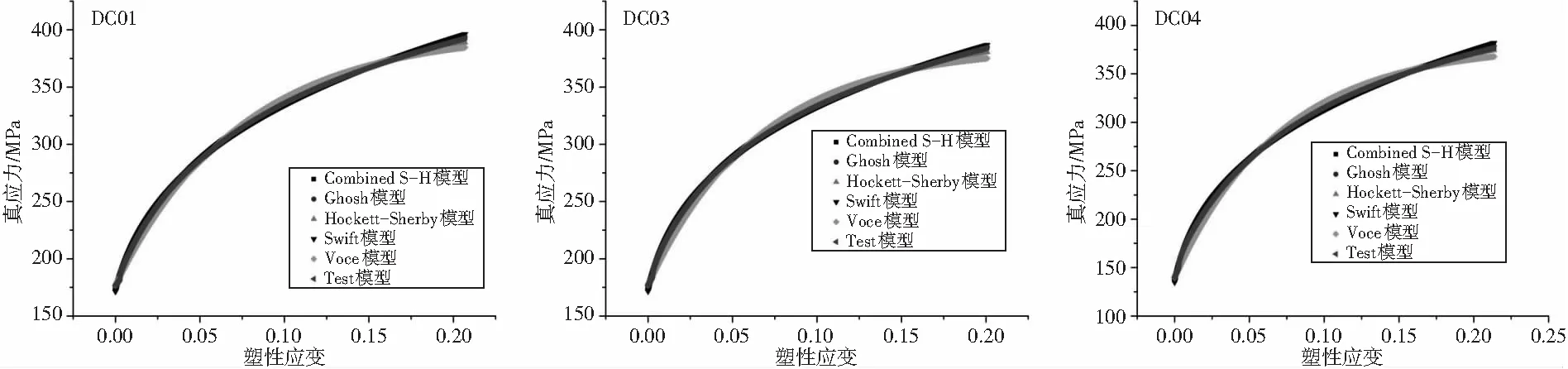
(a) (b) (c)

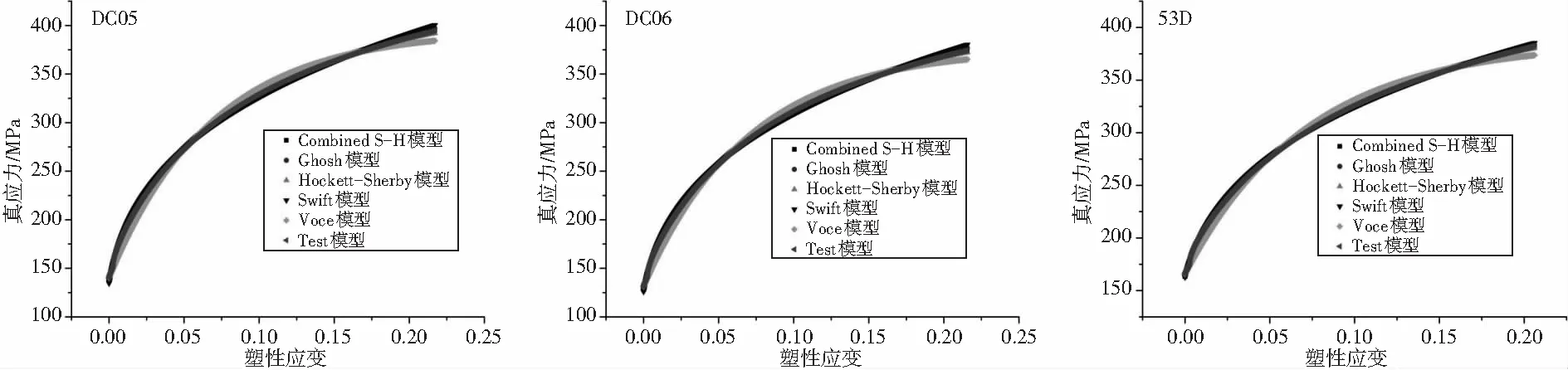
(d) (e) (f)

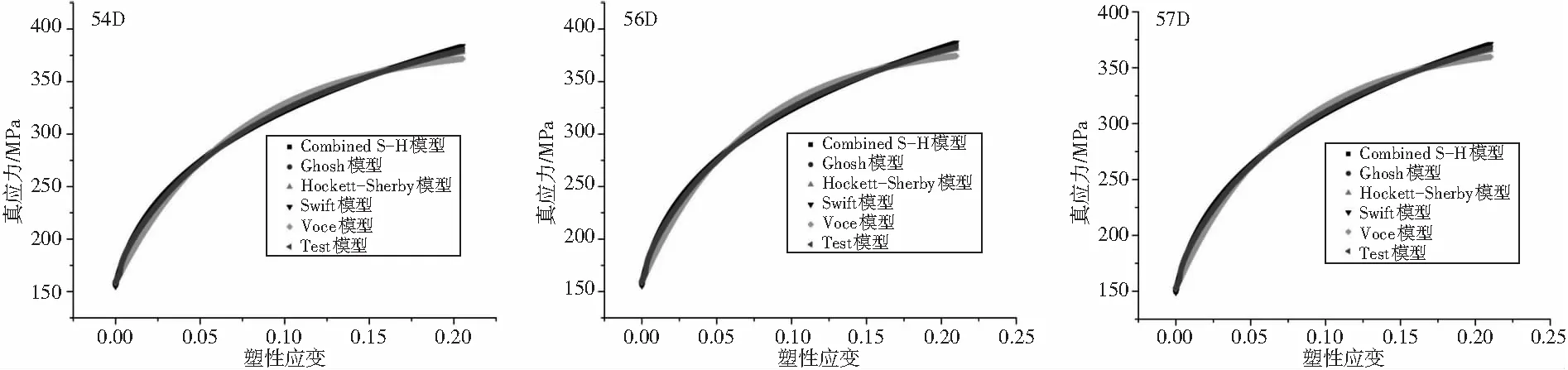
(g) (h) (i)图3 拟合结果

2.2 拟合分析

考虑到曲线拟合的起点、终点、误差绝对值及误差分布，从均方根、相关参数、屈服强度及均匀应变四个方面分析了拟合精度。

2.2.1 均方根分析

拟合曲线与试验曲线之间的均方根误差，结果见图4。

图4 DC系列不同模型拟合的均方根

2.2.2 相关系数分析

相关系数结果见图5，可以看出5种模型的相干系数均大于0.98，其中，Combined S-H模型在0.9995到1之间，Ghosh模型在0.9995左右，Hockett-Sherby和Swift在0.9995至0.990之间，Voce模型在0.9980到0.9955之间，Combined S-H模型相关系数最高。

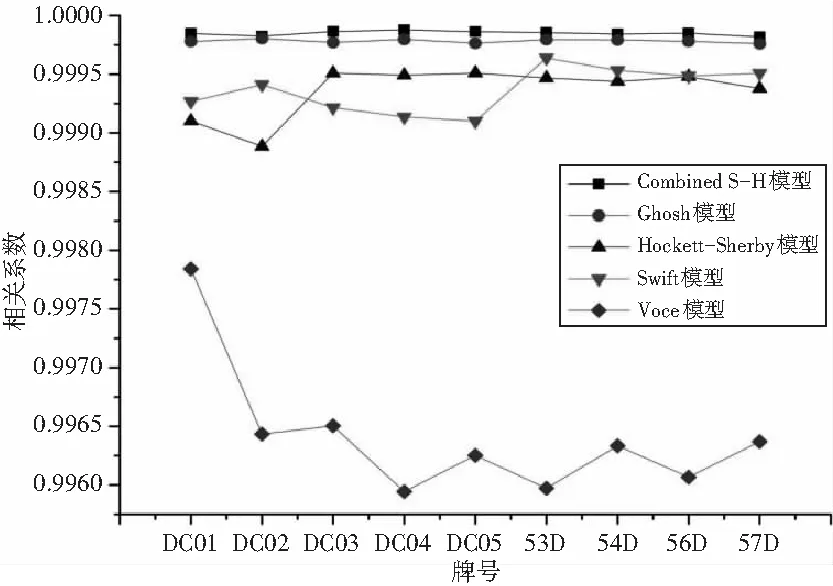
图5 DC系列不同模型拟合的相关系数

2.2.3 均匀应变分析

均匀应变对应抗拉强度，表征拉伸曲线的最高点。流动应力模型的均匀应变可以下式求解。

dσ/dεpl=dσ

(6)

不同模型预测的均匀应变见表2，其与试验值的误差绝对值占试验值的百分比见图6。

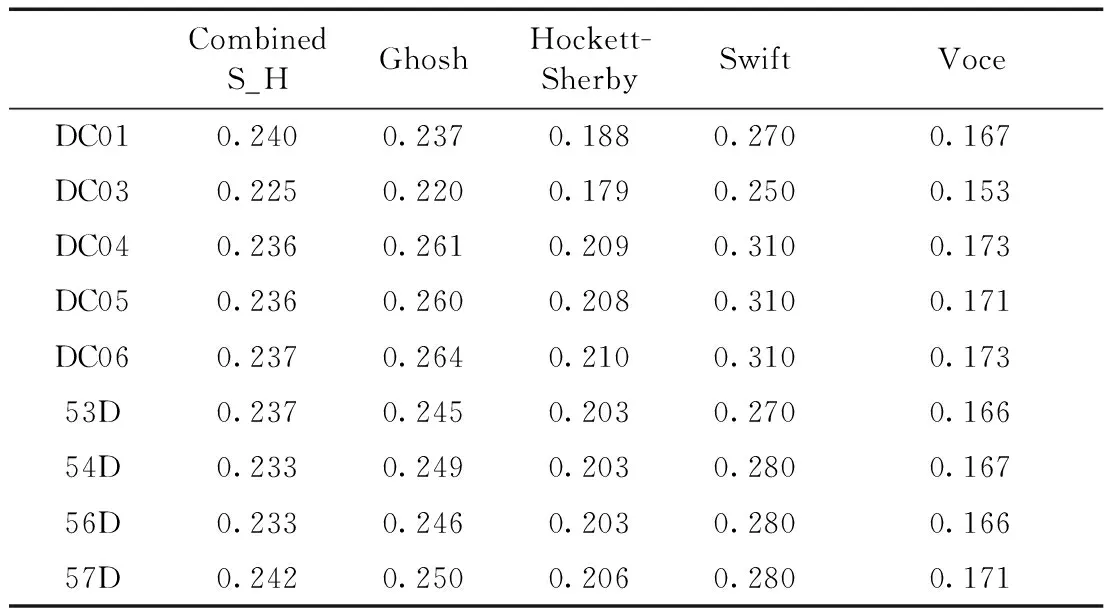
表2 五种流动应力曲线预测的均匀应变

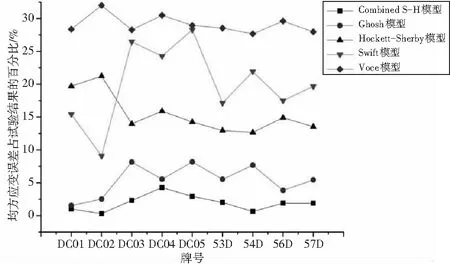
图6 DC系列不同模型拟合的均匀应变误差占试验值的百分比

从图6可以看出，Combined S-H预测的误差在0到2.25%之间，Ghosh模型预测的误差在2.25%到15%之间，Hockett-Sherby模型和Swift模型预测的误差在10%到27.5%之间，Voce模型在27.5%到32.5%之间，Combined S-H模型均匀应变的预测精度最高，其次为Ghosh模型，再次为Hockett-Sherby和Swift模型，Voce模型均匀应变的预测精度最差，其与预测精度最高模型对均匀应变预测的精度偏差高达到32%。

2.2.4 屈服强度分析

屈服强度是流动应力曲线的初始点，标志着塑性变形的开始，所以从屈服强度角度分析拟合精度，零εpl得到模型屈服强度，其值与试验值偏差占试验值的百分比见图7。

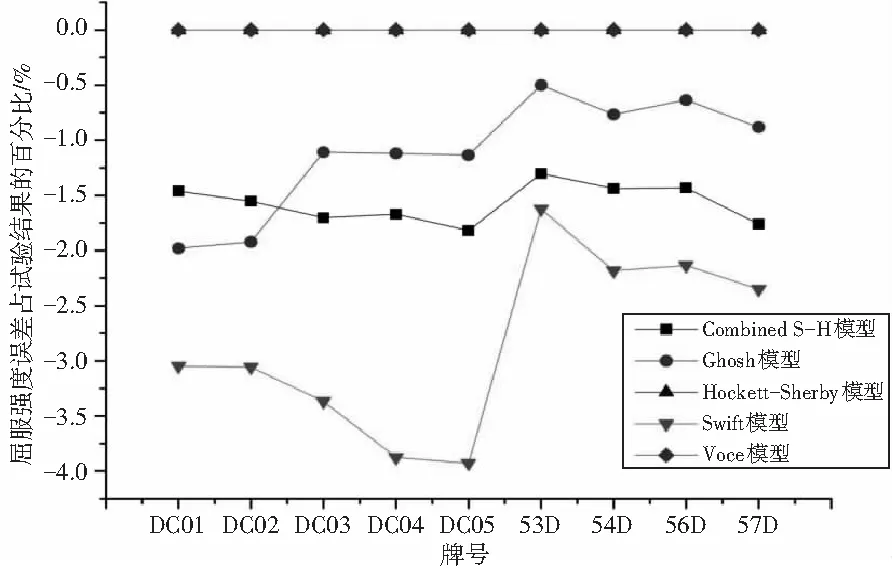
图7 DC系列不同模型拟合的屈服强度误差

从图7可以看出，由于Voce模型和Hockett-Sherby模型将屈服强度作为明确参数所以其误差为零。而Ghosh、Combined S-H、Swift模型中未明确屈服强度作为初始值，其预测值相对于试验结果都偏小，其中Ghosh模型预测值误差在-1.55%到0之间，Combined S-H预测值误差在-1.5%到-1%之间，Swift模型在-3.55%到-1.5%之间。

3 大应变范围流动应力模型比较

由上述分析可以发现，在均匀应变范围内，五种流动应力模型的相关系数都大于0.98，均方根在0～6之间，拟合精度都很高。

但是，由图8发现，在大应变范围内，不同模型开始出现较大差别，但对于DC系列深冲钢，存在一定的规律性。首先，由上到下依次为Swift、Combined S-H或Ghosh、Hockett-Sherby、Voce。其次，除了DC01和DC03之外，其他牌号的Combined S-H和Ghosh流动应力模型基本一致，再次，Swift、Combined S-H、Ghosh模型在大应变范围内持续增长，最后，Hockett-Sherby和Voce模型增长趋于平缓或饱和。前者大于后者且两者差值基本趋于定值。

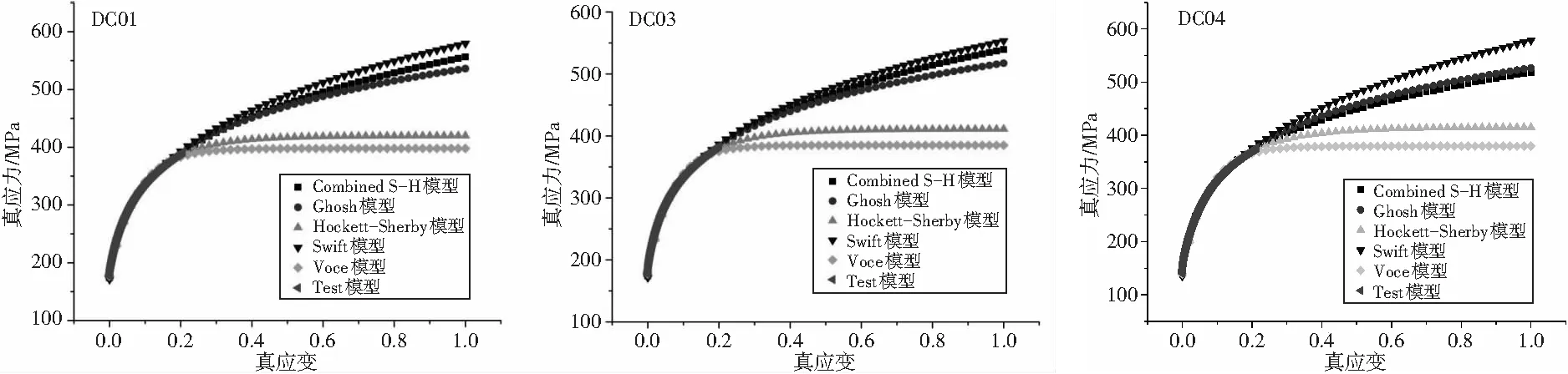
(a) (b) (c)

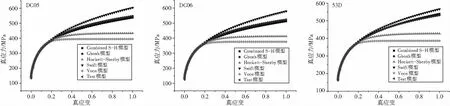
(d) (e) (f)

(g) (h) (i)图8 大应变阶段不同流动应力模型比较

为了比较不同模型在大应变阶段的预测精度，将这些模型应用在DX54[6]单向拉伸试验上，并和液压胀形试验结果对比，见下图9。模型与单向拉伸试验拟合结果的均方差、相关系数见表3。不同流动应力模型拟合曲线与液压胀形试验结果的统计分析结果见表4。

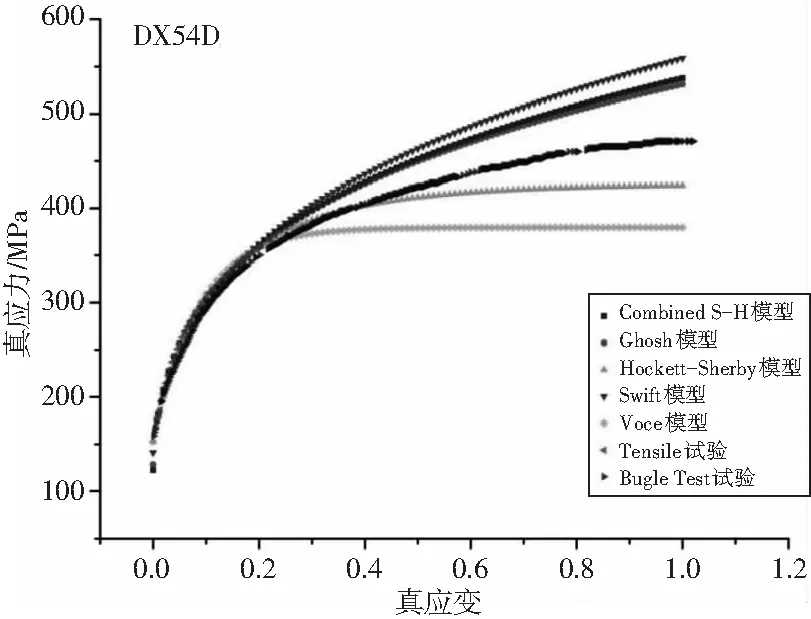
图9 DX54材料不同流动应力模型比较

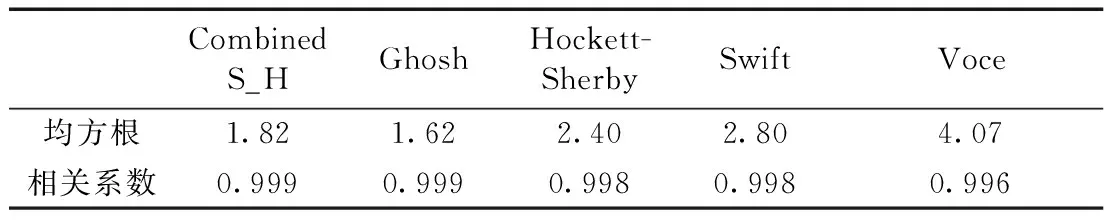
表3 常用流动应力模型对单向拉伸试验拟合结果

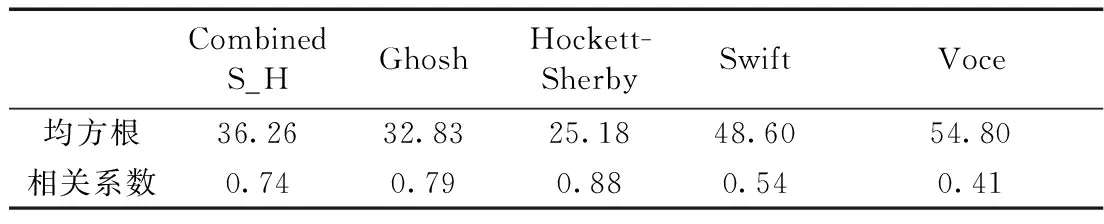
表4 常用流动应力模型拟合曲线与液压胀形试验之间的误差

从图9和表4可以看出，对于DX54，首先，从上到下，模型依次是Swift、Combined S-H或Ghosh、Hockett-Sherby、Voce模型。其次，Ghosh和Combined S-H模型两者之间相差小。最后，Hockett-Sherby模型与液压胀形试验结果最为接近。

从表3可以看出，五种常用流动应力模型相关系数基本一致，均方根由大到小的顺序为Ghosh、Combined S-H、Hockett-Sherby、Swift、Voce模型。

结合图9、表4和表3，不同模型在均匀变形范围内均方根都较小，且相关系数都很高，综合来看常用流动应力模型拟合精度都很高。但是在大应变范围内，Swift模型预测结果偏大，Ghosh与Combined S-H模型次之，Voce模型预测结果偏小，Hockett-Sherby模型次之，但是Hockett-Sherby模型预测结果与试验更为接近。

通过对比图8和图9，可以发现，对于DC01、DC03、DC04、DC05、DC06、53D、54D、56D、57D及DX54，在均匀变形范围内，模型都可以很好地预测变形能力，而在大应变范围内，模型预测差异变大，但是存在一定的规律性。首先模型测值由大到小分别为Swift、Ghosh或Combined S-H、Hockett-Sherby、Voce模型，其次，Ghosh和Combined S-H很接近，Hockett-Sherby和Voce差值趋于定值。

4 结 论

研究了五种常用流动应力模型在均匀变形范围内对DC系列深冲钢拉伸曲线的适用性和大应变范围内模型预测的规律。

(1)在均匀变形范围内，Combined S-H、Ghosh、Hockett-Sherby、Swift、Voce模型的相关系数都在0.99以上，相差很小。均方根在6%以内，模型的拟合精度都非常高。精度最高的为Combined S-H和Ghosh模型，次之为Hockett-Sherby和Swift模型，再次之为Voce模型。

不同流动应力模型对均匀应变预测能力相差较大，在均匀应变范围内成形时，涉及均匀应变的相关成形准则应重点考虑该差距。

(2)在大应变范围内，常用五种流动应力模型的差异逐渐变大，但是存在一定的规律性。模型预测值由大到小依次是Swift、Combined S-H或Ghosh、Hockett-Sherby、Voce模型。Combined S-H与Ghosh模型重合度高。Hcokett-Sherby和Voce模型差值趋于定值。

对于DX54材料大应变范围内，Swift模型预测值最大，Voce预测值最小，液压胀形试验值在Ghosh(或Combined S-H)预测值与和Hockett预测值之间，而Hockett模型预测结果与液压胀形试验结果最为接近。