某水利枢纽工程混凝土防渗墙模量变化计算分析
吕 智
(塔城地区水利水电勘察设计院,新疆 塔城 834700)
0 引 言
随着土石坝的不断发展,人们对于工程安全程度的要求越来越高[1]。土石坝因其较多的优点得到快速发展,但同时也发生过较多的事故。其中由于稳定及渗透方面原因导致破坏的事例已经越来越少,而由于不均匀变形引起的高土石坝裂缝问题较为普遍,由此引发的渗漏造成坝体破坏的事例较多[2]。土石坝的抗裂设计一直是设计人员关注的重点。坝体在施工过程中,由于施工高度的不断增加,土体不断被压缩产生沉降以及孔隙水压力的慢慢消散,坝体的不均匀沉降导致大坝产生裂缝从而引起渗漏甚至溃坝、垮坝等,因此进行土石坝的应力和变形计算就显得尤为重要[3]。
1 工程概况
某坝位于哈木勒提沟沟口上游约300 m处,工程所处地形俯视图呈U形,河谷宽约280 m。两岸边坡右陡左缓,山体岩石大部分裸露,可开采性好。坝肩基岩相对完整,仅有一些小断层的发育,且强风化层较浅,所以基岩性质较稳定。坝轴线呈直线状,且倾向上游,轨迹和两岸岸坡基岩走向近乎平行,这种坝轴线的布置方法有利于两岸洞室围岩的稳固和基础防渗。但也存在一些不利的工程条件,如砂层分布于坝底的两侧,纵向长约380 m以上,横向宽约170 m以上,埋藏深度19~32 m,最大深度达44 m左右。漂石和冰碛层主要包括卵石层和块石层,透水性极强且分布不均,在性质上属于中强透水性,很不稳定,建议予以挖除。其属下更新时期(Q3)晚期的水冰沉积物,颗粒组成主要为细砂,其中又内含角砾、碎石、粗砂,密实度较好,此深厚覆盖层地基上层属由淤泥质组成的黏土层。该工程坝基深覆盖层的深度极大且地质条件非常复杂,在国内外大坝建设中属于难度较大的,因而对该深覆盖层坝基的应力变形和防渗的设计显得十分重要[4]。
1.1 边界条件及初始条件的确定
为了更精确地计算坝体的受力和位移,模拟坝体、坝基以及两岸岸坡的真实地形地貌,在建模过程中,沿水流方向对地基进行适当的延伸(各150 m)。为更好地模拟坝体变形,在顺河流方向的边界上,在模型的底部进行全约束;模型左右两面即侧向施加X轴方向的面约束,在模型的前后施加Y方向的面约束,这样模拟边界条件能更好地说明坝体的各项受力情况[5]。
因为力学性能的不同,在材料与材料之间需要设置接触面单元,以便更好地传导外部和内部荷载。本文在坝基中的砂层和冰碛层间、混凝土防渗墙与地基的接触面之间均设置了接触面单元,采用单元均为ANSYS软件自带的3-D单元。因在坝体底部和基岩的材料差异甚大,为了更好地模拟现实情况,在二者之间也设置了接触面单元。
1.2 施工模拟的程序思路
在利用ANSYS进行土石坝有限元模型的施工模拟时,先建好整体模型,然后分区定义不同材料的材料参数,定义包括材料密度初始弹性模量和初始泊松比,命令流为mat,mp,lab,co。其中lab为ex时表示弹性模量,lab表示待定义的特性项目,泊松比为nuxy,密度为dens。材料特性值表示为co,材料编号表示为Mat。然后给模型划分网格,为了方便以后提取单元,再分别给每个单元或单元组定义材料号。计算之前还需设置边界条件,其定义是坝体底部设置全约束,坝体其他面设置和坝轴线相垂直的约束,再按照平面应变进行计算。本文根据邓肯E-B模型在ANSYS中的实现方法和分层加荷的必要性,在参考大量文献的基础上,采用二次开发APDL语言编制土石坝施工模拟的计算程序。其基本思路如下[6-7]:
1)根据施工模拟的过程,在坝体阶段分层建模,划分网格后逐层设置材料参数。因为进行施工模拟时采用ANSYS中的生死单元命令,在网格步骤时要用命令将所有的坝体单元杀死,然后根据施工模拟依次激活相应的坝体单元。
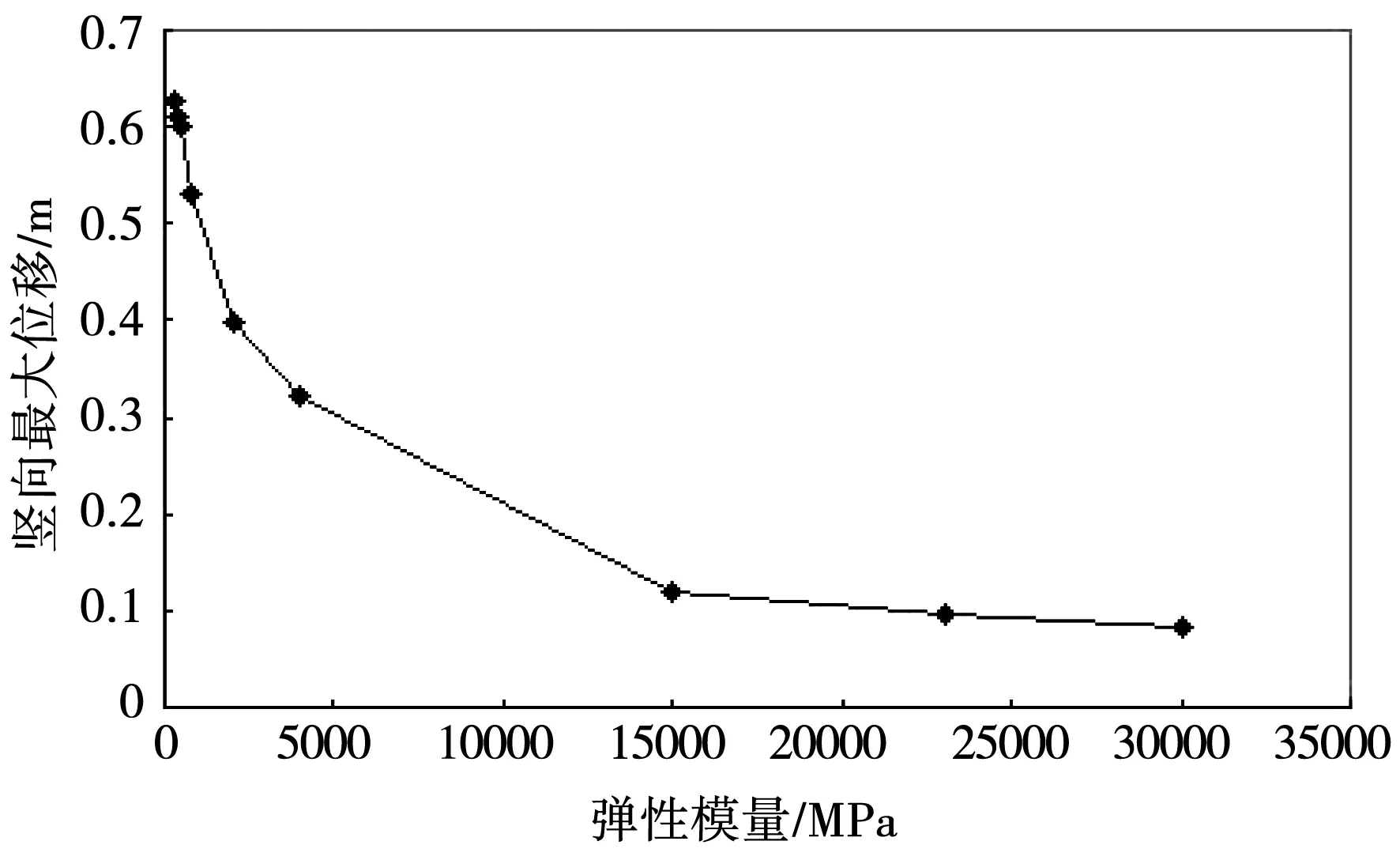
2)编制Duncan E-B本构关系的宏命令,根据计算结果判断荷载,当σ1-σ3<(σ1-σ3)0,且S 3)激活最下部分的单元,此时自重为第一层的重力。施加第一步坝体单元的荷载,根据初始弹性模量判定。在上述计算显示的基础上,利用宏命令提取各单元的第一主应力和第三主应力。命令流为establa,battal,a,l和establa,battal3,a。将结算结果利用宏命令提取的大小应力分别赋值给数组第三、第一主应力。在对上述结果的分析提炼上,调用宏命令,在大小应力计算结果基础上,计算出新的参数,并且修正当前的程序包括弹性模量和泊松比。施加第二步荷载,激活下一层单元,利用中点增量法求得新单元的参数,并且相应地修改上述数值。分级加荷,方法同上,直到坝体分级施工结束。Duncan模型中Eur与Et的差别反映出加荷过程对大坝的应力-应变。Bt是p与εv之比,关系式如下: Bt=Et/3×(1-2×vt) 4)重复上述步骤,逐层激活各层单元进行计算,直到施工过程结束。 5)得出计算结果,绘制曲线。 以上详细介绍了土石坝施工模拟的实现过程。在ANSYS中将荷载分成若干级的荷载增量,各级荷载之间的刚度矩阵变化、弹性模量的变化和泊松比的变化都导致了材料之间的性质变化,由此反映出非线性的应变关系。 本文所述的某水利枢纽工程的混凝土防渗墙深度达85 m以上,在全国范围内尚属首次[7]。防渗墙的应力变形多种多样,而防渗墙的弹性模量数值变化对墙体应力应变的影响是一个值得研究的问题。为了配合防渗墙现场施工以及给工程提供相对准确的设计数据,需要给出合理的混凝土配合比。在同一密度不变的前提下,改变混凝土的弹性模量和泊松比,数据见表1。 表1 各方案混凝土防渗墙弹性模量及泊松比 混凝土防渗墙在不同泊松比和弹性模量条件下,由于防渗墙嵌入基础之内,各方案的水平位移较小,没有较大的差异。在防渗墙的上部发生最大的竖向位移,各种工况下的应力水平值均较小;但是也存在着最大值,在砂层和防渗墙结合部分的上方达到竖直正应力σy的最大值。由表2和图1、图2可知,在该工况下防渗墙的弹性模量不断增加,对应的竖向应力亦增加。当弹性模量由268 MPa变化至30 000 MPa时,竖向最大应力从所对应的5.94 MPa增大为25.3 MPa。弹性模量-应力变化曲线显示,弹性模量为5 000 MPa时是个分水岭。当大于5 000 MPa时,弹性模量增加,则竖向最大应力也随之慢慢增加;当小于5 000 MPa时,弹性模量增加,竖向最大应力则增大的幅度较大。而位移-弹性模量变化曲线显示,此种变化和前者类似,只不过前者是缓慢增加或是迅速增大,后者却是缓慢减小或是快速减小。 表2 竣工期防渗墙最大应力、位移计算结果表 图1 竖向最大应力随弹性模量变化曲线(竣工期) 图2 竖向最大位移随弹性模量变化曲线(竣工期) 由计算结果曲线可知,与竣工期相比,蓄水期时的防渗墙向下游水平位移有所增大,而竖向位移却在降低,这是由于受到水压力和压力的原因所致。由表3和图3、图4可知,蓄水期时防渗墙的应力与位移变化和竣工期的规律性一致。混凝土防渗墙弹模增加,竖向正应力也增加。此时,在弹性模量由268 MPa增大至30 000 MPa的过程中,竖向最大正应力由7.05 MPa增大至25.3 MPa。弹性模量-应力变化曲线显示,弹性模量为5 000 MPa时是个分水岭。当大于5 000 MPa时,弹性模量增加,则竖向最大应力也随之慢慢增加;当小于5 000 MPa时,弹性模量增加,竖向最大应力则增大的幅度较大。而在弹性模量-位移的变化曲线结果图中可知,计算结果和竣工期相似,但是竖向位移均比竣工期的减少。其原因是土体接触水后,土体之间的相互黏结使有效重量减小,从而导致此种影响的产生。 表3 蓄水期防渗墙最大应力、位移计算结果表 图3 竖向最大应力随弹性模量变化关系曲线(蓄水期) 图4 竖向最大位移随弹性模量变化关系曲线(蓄水期) 本文采用三维实体有限元模型,在ANSYS中使用大量八节点六面体单元和少量四节点四面体单元,以求与实际工程最相符的模拟坝体从施工期到运行期的全过程,综合ANSYS中的二次开发语言APDL的程序特性,在实现各种筑坝材料软件强大的处理功能和近似计算的基础上,对该工程的应力-应变进行了数值模拟,得到了大坝在两种工况下的应力应变和位移的变化曲线,与工程实际相符。主要结论如下: 1)防渗墙的弹性模量与应力有着直接的关系,降低弹模值,相应的应力值亦会减小,且防渗墙与地基的接触部位发生了竖向最大应力。通过对比得知,防渗墙弹性模量为5 000 MPa时是个临界点,小于此值时,防渗墙竖向应力变化较为显著,当大于此值时变化稍显迟钝,差距不大。 2)防渗墙的弹性模量也与位移有着直接的关系,增大弹模值,相应的位移变化会减小,且防渗墙的最上方发生了竖向最大位移。防渗墙的弹性模量-竖向位移敏感性分析同弹性模量-竖向应力结果。2 混凝土防渗墙模量变化计算结果与分析
2.1 计算工况

2.2 竣工期



2.3 蓄水期


3 结 论

