交通荷载对底部隐伏溶洞的动力响应分析*
张军, 蔡虎宇, 廖鑫捷
(1.长沙理工大学 土木工程学院, 湖南 长沙 410114;2.深圳市综合交通设计研究院有限公司, 广东 深圳 518110)
公路隧道修建过程中难免要穿越岩溶区域。针对隧道底部隐伏溶洞导致的安全隐患,文献[2-3]对岩溶地区隧道由于溶洞的存在而引发的附近地表沉降进行了分析;文献[4]指出防突层的整体性和岩溶水压大小是导致防突层破坏的主要原因;文献[5]建立了岩溶地区隧道底板的最小安全厚度理论计算公式;文献[6]通过隧道位移和结构内力来评定岩溶隧道的结构稳定性;文献[7]运用FLAC3D软件分析了不同大小溶洞对隧道围岩应力及变形的影响;文献[8]运用有限元软件ABAQUS对围岩受力和位移的变化进行了数值分析;文献[9]通过现场监测、数值模拟对高水压下岩溶隧道支护结构的受力特征进行了分析。虽然近些年来诸多学者对岩溶隧道的位移展开了研究,但关于岩溶隧道在交通荷载作用下的稳定性分析较少。该文结合湖南张桑(张家界—桑植)高速公路白龙庵隧道,运用MIDAS-NX软件进行计算分析,研究交通荷载作用下隧道围岩应力与位移的变化,分析隐伏溶洞不同间距对隧道围岩稳定性的影响。
1 交通荷载的简化与确定
早期研究将交通荷载简化为静止土柱来考虑,忽视了交通荷载的动态性对地基的影响;后来逐渐关注到交通荷载对地面沉降的影响,确定车轮与路面的接触面积,通过轴载换算将交通荷载模拟成移动荷载进行计算;再后来就是考虑车辆荷载在运动过程中造成的振动性,将交通荷载等效为恒载作用、移动恒载作用、半波正弦荷载作用等进行分析。但由于交通荷载本身速度与质量的多样性及地基参数的差异性等,目前对交通荷载对路基受力、位移等的影响还没有具体界定。
采用JTG D50—2006《公路沥青路面设计规范》中的标准轴载设计参数,单轮传压面圆半径d=21.30 cm,单个轮胎竖向荷载为25 kN,轮胎接地压强为0.7 MPa。标准轴载Bzz-100两轮中心距为1.5d,轴距为2.0 m,荷载对称作用在道路两侧,隧道内交通荷载作用位置见图1。将交通荷载等效成一种简单正弦荷载,在分析时段内的任意时刻t,作用于某一点的交通荷载可换算为在该点正上方的半正弦荷载。假定整个分析时段为Ta,半正弦荷载作用时间为T,则车辆荷载与时间的关系为:
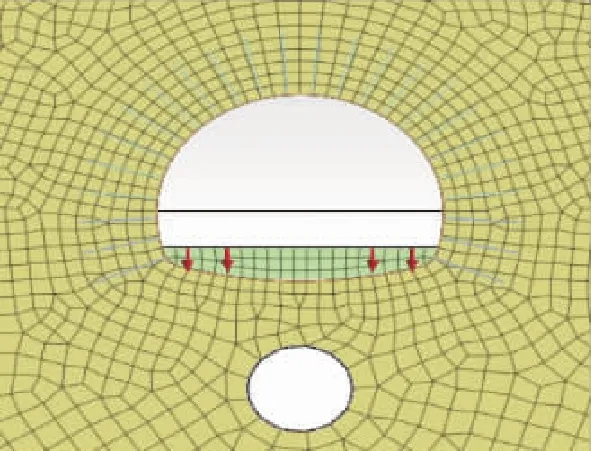
图1 车辆荷载作用示意图
取荷载作用时间T=0.057 51 s,分析时段Ta=为0.2 s,时间步长为0.025 s,车辆行驶速度v=80 km/h,分析时程内车辆荷载函数曲线见图2。

图2 车辆荷载函数曲线
2 有限元模型的建立
运用MIDAS-NX建立白龙庵隧道数值计算模型,模型设计参数依据Ⅴ级围岩相关参数和隧道设计参数选取。由于隧道为双向两车道,采用对两车道路面施加集中力的方式模拟交通荷载对隧道的作用力,集中力通过软件运用正弦函数施加时程荷载函数来模拟。网格模型见图3。

图3 隧道有限元模型网格图
白龙庵隧道仰拱采用40 cm厚C25砼,路面采用复合路基材料,主要为20 cm厚C20砼基层、24 cm厚连续配筋砼层。钢筋砼的弹性模量按经验公式(EsAs+EcAc)/(As+Ac)计算(Es、Ec分别为钢筋和砼的弹性模量;As、Ac分别为钢筋和砼的截面积),其他参数依据表1选取。
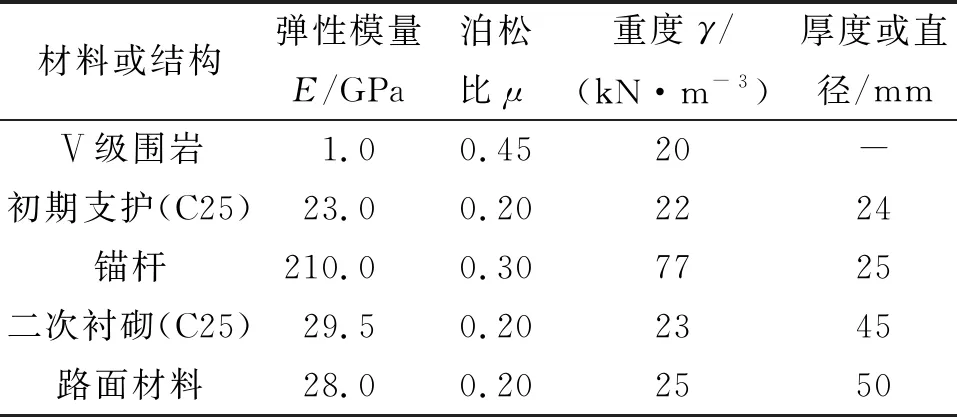
表1 力学参数
3 数值模拟分析
取溶洞半径R=2 m,分析溶洞顶部距隧道底部距离L为1 m、3 m、5 m、7 m时,在动载和恒载作用下溶洞顶部位移和隧道位移、应力分布。
3.1 隧道不同部位的位移与时间关系分析
溶洞位于隧道拱底不同位置时,交通荷载作用下隧道各部位的位移时程曲线见图4~7。

图4 L=1 m时交通荷载作用下隧道各部位的位移时程曲线
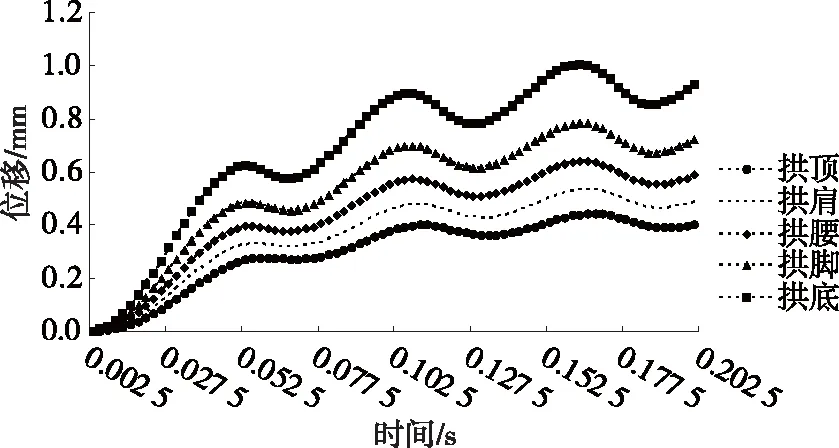
图5 L=3 m时交通荷载作用下隧道各部位的位移时程曲线

图6 L=5 m时交通荷载作用下隧道各部位的位移时程曲线

图7 L=7 m时交通荷载作用下隧道各部位的位移时程曲线
由图4~7可知:在交通荷载作用下,隧道各部位发生不同程度的变形,随溶洞距隧道拱底距离的增大,隧道位移减小;L=1 m,t=0.162 5 s时,拱底位移出现峰值,最大位移为1.043 3 mm,此时交通荷载对拱顶的影响最小。
3.2 不同荷载作用下隧道竖向位移分析
溶洞位于隧道拱底不同位置时,隧道拱顶、拱肩、拱腰、拱脚、拱底在不同荷载作用下的竖向位移见图8、图9。

图8 动载作用下隧道各部位的最大竖向位移

图9 恒载作用下隧道各部位的最大竖向位移
由图8、图9可知:在交通荷载作用下,隧道拱顶、拱肩、拱腰部位产生微小位移,并随溶洞与隧道底部距离的增大而逐渐减小;交通荷载对隧道拱底位移的影响最大,且随溶洞距离的增大逐渐减小。动载作用下,L=1 m时拱底位移为-1.043 3 mm,L=7 m时拱底位移为-0.941 7 mm,比L=1 m时减小9.7%;恒载作用下,L=1 m时拱底位移为-1.558 7 mm,L=7 m时拱底位移为-1.407 6 mm,比L=1 m时减小9.7%。
3.3 不同荷载作用下溶洞顶部竖向位移分析
溶洞位于隧道拱底不同位置时,溶洞顶部在不同荷载作用下的竖向位移见图10。
由图10可知:车辆荷载向下传递,溶洞顶部的位移较大,但随着与隧道底部距离的增大,荷载往下传递的力衰减,对溶洞的影响逐渐减小。溶洞的存在是影响隧道稳定性的不良隐患。

图10 不同荷载作用下溶洞顶部竖向位移
3.4 不同荷载作用下隧道最大主应力分析
溶洞位于隧道拱底不同位置时,隧道拱顶、右拱腰、右边墙、拱脚及拱底部位的最大主应力见图11~15。
由图11~15可知:相较于隧道其他部位,隧道拱脚部位的最大主应力更大,说明该部位受交通荷载的影响较大,容易产生应力集中而破坏。根据曲线斜率,隧道底部的变化率最大。动载作用下,L=1 m时底部最大主应力为113.17 kPa,L=7 m时底部应力为-3.67 kPa;恒载作用下,L=1 m时底部最大主应力为124.08 kPa,L=7 m时底部应力为-4.53 kPa。随着溶洞与隧道底部距离的增大,隧道底部应力变化明显。
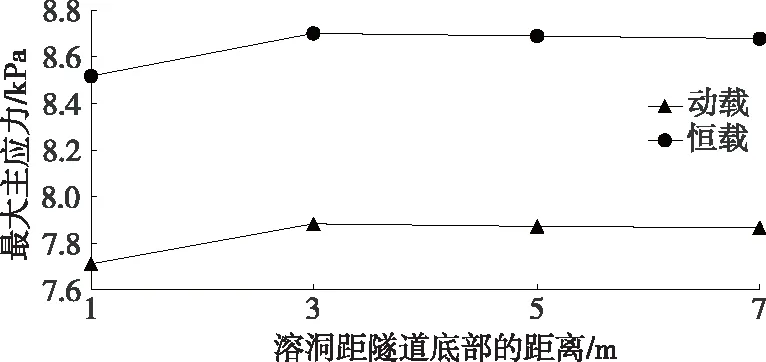
图11 不同荷载作用下隧道拱顶的最大主应力曲线
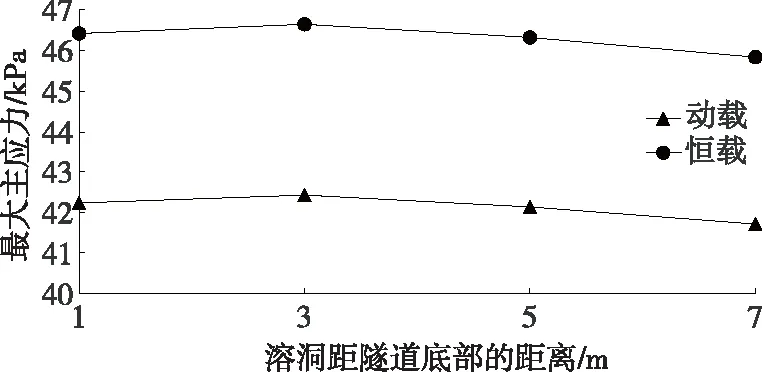
图12 不同荷载作用下隧道右拱腰的最大主应力曲线
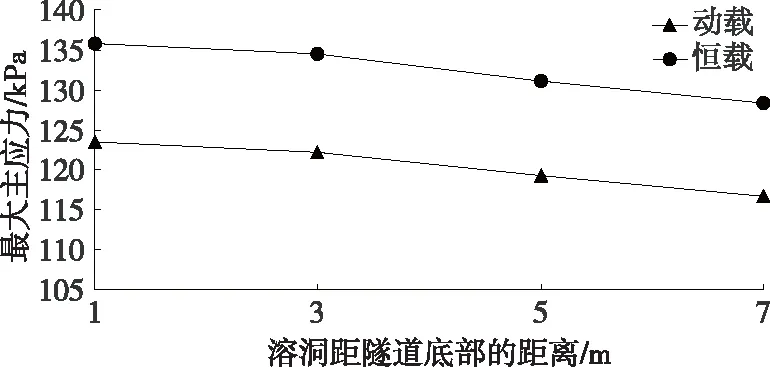
图13 不同荷载作用下隧道右边墙的最大主应力曲线
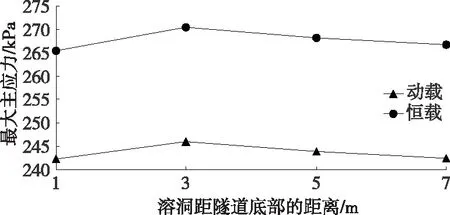
图14 不同荷载作用下隧道拱脚的最大主应力曲线
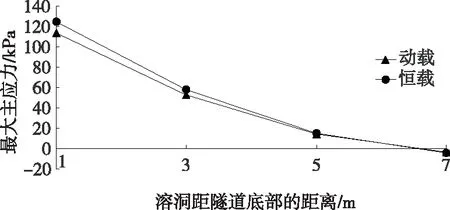
图15 不同荷载作用下隧道拱底的最大主应力曲线
3.5 振动速度分析
下伏溶洞距隧道底部距离为1 m时,交通荷载作用下隧道拱顶、拱腰、边墙、拱脚、拱底的最大振动速度见表2。

表2 交通荷载作用下隧道各部位的最大振动速度
由表2可知:交通荷载对隧道的影响主要集中在拱底位置,振动速度最大值为1.203 cm/s,对其他位置的影响较小,且随着与溶洞距离的增大而逐渐减小;不同部位最大振动速度出现的时间不同,拱底最大振动速度出现在0.172 5 s,随时间递增,其他部位相继出现最大振动速度,体现了振动随时间传递的过程。
4 结论
(1) 在隧道路面两侧施加半波正弦动荷载,溶洞与隧道底部的距离不同时,交通荷载作用下隧道拱底的位移最大,且各部位的位移随溶洞距离的增大而减小。
(2) 动载和恒载作用下,溶洞与隧道的距离是影响隧道稳定性的主要因素之一,溶洞距隧道底部1 m时,隧道各部位的位移和主应力最大,随距离增大位移和主应力逐渐减小。
(3) 恒载和动载对隧道稳定性都有一定影响,恒载对隧道各部位的影响大于动载。动载的模拟更能反映汽车所产生的冲击力随时间的变化,能更真实地反映交通荷载对隧道的影响。

