悬索桥主梁施工过程设铰数量对结构体系的影响分析*

陈浩， 潘权， 韩伟威

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114；2.长沙理工大学 交通运输工程学院， 湖南 长沙 410114)

悬索桥主跨1 000 m以下的主梁节段吊装中，一般采用缆索吊机单边或双边起吊从中跨向边跨对称施工，随着梁段架设数量的增加，加劲梁线形慢慢向下凹，待吊装到约1/4跨时出现反拱，合龙后的加劲梁线形为上拱状态。在此过程中，整个结构体系会产生较大位移变化，如不在合适位置安装临时连接，会导致钢桁梁杆件承担较大的应力变化，且杆件与杆件的连接位置易出现应力集中现象，甚至发生螺栓失效断裂或连接板屈曲破坏。主梁节段间施工中全部铰接能很好地控制钢桁梁安装中产生的应力，但会导致临时铰数量增大，费用提高，后续刚接任务重，桥面板不能焊接成型，不能平行作业，从而增加工期。且大部分悬索桥主梁体系转换过程省去了二恒等代工序，在结构体系没有达到自然合龙条件时就强行合龙，导致桁梁杆件拼装应力滞留在钢桁梁杆件内。如果钢桁梁杆件在初步设计中未考虑这些因素，会导致钢桁梁杆件应力超过结构容许应力。该文以湄潭至石阡高速公路河闪渡乌江大桥主梁施工为工程背景，对比分析主梁节段施工中采用全部铰接、2段设铰、3段设铰、4段设铰、6段设铰对钢桁梁杆件应力、桥面线形、主缆线形、吊索索力、梁段下缘开口宽度等的影响。

1 工程概况

河闪渡乌江大桥布置形式为249 m+680 m+238 m，主桥为全长680 m单跨钢桁梁悬索桥，设计标准为双向四车道公路一级，设计速度为80 km/h(见图1)。主桥加劲梁采用板桁结合形式，主桥在成桥状态下中跨矢跨比为1/10，主缆横向中心间距为27.0 m，纵向吊索标准间距为13.0 m，上弦杆中心到下弦杆中心6.8 m，标准节段长13.0 m，钢桁梁标准断面见图2。加劲梁共有3 569个杆件，属于带竖腹杆的华伦式结构，上下弦杆为封闭箱形结构，其余杆件为工字形结构。铰接处只在上弦杆设置临时铰，下弦杆及其余杆件为完全放开状态，采用两两刚接，每2个梁段设置一道临时连接。

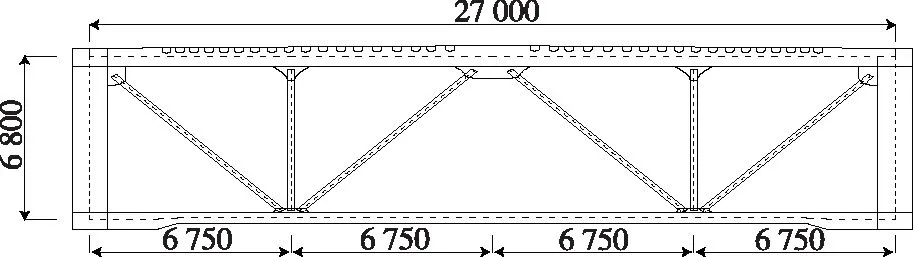
图2 河闪渡乌江大桥钢桁加劲梁断面示意图(单位：mm)

2 有限元仿真分析

2.1 分析计算理论

悬索桥的大跨径、大变形、大位移特性，使其受力本质上接近柔性索悬挂体系，在荷载作用下会产生大变形，即大变形效应，计算分析中必须考虑这类非线性影响。

悬索桥在受到外界荷载作用时，不仅主缆、加劲梁会向下沉，主塔也会被压缩，吊杆会受拉，结构平衡应根据其受力后的平衡位置来决定。受大位移的影响，平衡方程不再是线性关系，小位移假设中的叠加原理也不再适合，在计算内力或线形时需考虑位移的影响即大位移理论。其平衡方程为：

([k1]+[k2]+[k3]){Δd}={ΔR}

(1)

式中：[k1]为弹性刚度矩阵；[k2]为几何刚度矩阵；[k3]为大位移刚度矩阵；{Δd}为节点位移增量矩阵；{ΔR}为节点荷载增量矩阵。

采用有限元软件建立乌江大桥有限元模型(见图3)。主桥面系中除桥面板采用板单元建模外，其余构件均采用梁单元建模；主塔也采用梁单元建模；主缆及吊索采用索单元建模。全桥共有2 062个节点、4 782个单元。采用Newton-Raphson法进行迭代计算，收敛准则以位移范数为基础，精度为0.001，每个施工阶段的计算结果达到该精度时停止计算。

图3 乌江大桥有限元计算模型

2.2 计算分析结果

选取吊装施工中一个施工阶段进行数据对比，标准梁段之间的节点板放置在已吊装梁段上，采用均布荷载模拟节点板放置在梁段上的受力情况，分析全部铰接、2段设铰、3段设铰、4段设铰、6段设铰施工工况下钢桁梁杆件应力、桥面线形、主缆线形、吊索索力、梁段下缘开口宽度。

2.2.1 加劲梁应力变化规律

加劲梁上下弦杆为主要受力构件，吊索与上弦杆相连，选取上弦杆应力进行对比分析。应力测点位于吊索吊点位置偏向桥塔一侧距离吊索1.625 m处，湄潭侧测点偏向湄潭侧，石阡侧测点偏向石阡侧。同时提取下弦杆纵向同一坐标位置应力作为对照。不同工况下上下弦杆最大、最小应力见表1、图4～8，最大、最小应力按照正负号区分。W13～E13代表从湄潭向石阡方向。

由表1、图4～8可知：1) 全部铰接工况下，上下弦杆应力变化稳定。上弦杆中只在两侧应力有较大变化，其余位置的应力大小接近一致，但应力相对其余设铰工况整体偏大。相比上弦杆，下弦杆应力变化更小，应力曲线为直线，而且接近无应力状态。2) 随着全桥分段设铰数量的减少，应力曲线锯齿状变化趋势增强。在2段设铰工况下，应力变化非常规律且应力较大的测点处应力相比全部铰接时无太大变化。剩余3种设铰工况下，上弦杆应力逐渐向压应力变化，下弦杆应力逐渐向拉应力变化，上弦杆中压应力与下弦杆中拉应力变化幅度非常大。3) 与全部铰接工况时相比，2段设铰、3段设铰、4段设铰、6段设铰工况下，上弦杆最大拉应力变化幅度分别为-5.7%、-8.8%、4.4%、7.9%，最大压应力变化幅度分别为-3.0%、3.0%、13.3%、48.5%；下弦杆最大拉应力变化幅度分别为0、250%、800%、2 775%，最大压应力变化幅度分别为106.3%、0、0、25%。可见，大段设铰会显著增大加劲梁吊装施工中杆件受力，影响结构受力安全。

表1 不同设铰工况下上下弦杆最大拉压应力 MPa

图4 全部铰接工况下上下弦杆最大、最小应力变化

图5 2段设铰工况下上下弦杆最大、最小应力变化

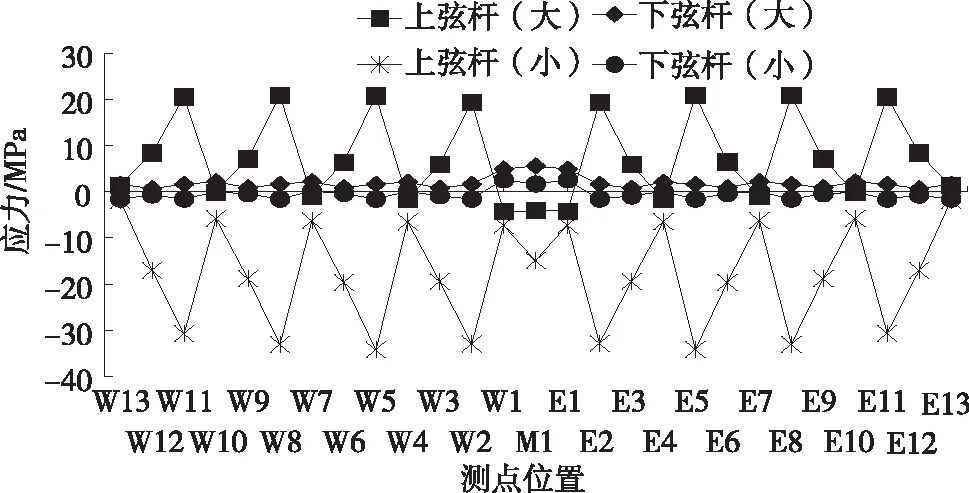
图6 3段设铰工况下上下弦杆最大、最小应力变化

图7 4段设铰工况下上下弦杆最大、最小应力变化

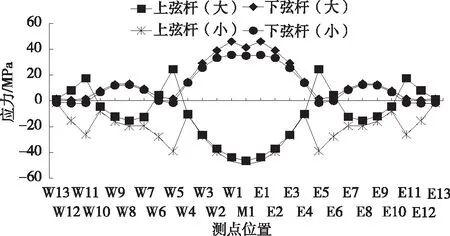
图8 6段设铰工况下上下弦杆最大、最小应力变化

2.2.2 加劲梁线形变化规律

加劲梁线形标高提取点位于吊索和加劲梁连接处，每个梁段上有1个吊点，故吊点编号以梁段编号表示。不同工况下梁段标高及加劲梁线形见表2、图9。

由表2、图9可知：不同设铰工况下，主梁线形主要在W3～E3梁段出现明显标高分层，其余位置标高大小较接近；6段设铰工况下，所有位置的标高最大；最小标高在不同位置出现在不同设铰工况中；W1～E1梁段标高变化最明显；全部铰接和2段设铰工况下标高差别很小且在所有工况中最小；随着设铰数量的减少，标高显著增大；W1、E1梁段标高在不同设铰工况下出现最大差值，为0.269 m。

表2 不同设铰工况下跨中区域W3～E3梁段标高 m

图9 不同设铰工况下加劲梁线形

2.2.3 主缆线形变化规律

主缆线形标高提取点位于吊索与主缆连接处，不同工况下索段标高及主缆线形见表3、图10。

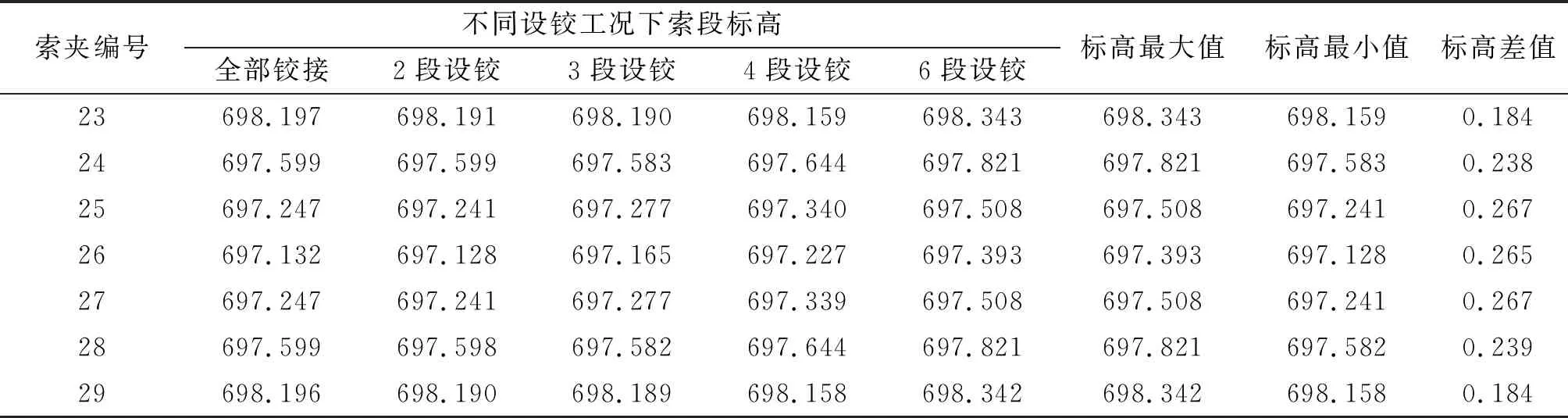
表3 不同设铰工况下跨中区域标高 m

图10 不同设铰工况下主缆线形

由表3、图10可知：主缆线形竖向标高只在跨中局部区域有较大变化，与加劲梁局部区域纵向坐标相同；随着设铰数量的减少，标高逐渐增大；主缆竖向最大标高差出现在25、27号索夹处；最大标高出现在6段设铰工况，最小标高出现在2段设铰工况，最大差值为0.267 m。

2.2.4 吊索索力变化规律

吊索索力分析采用前端吊索索力进行分析。图11为吊索索力对比，表4为不同设铰工况下最大前端吊索索力。

图11 不同设铰工况下前端吊索索力对比

表4 不同设铰工况下最大前端吊索索力 kN

由图11、表4可知：全部铰接工况下，不存在刚接的梁段，其吊索均位于铰接处，索力较大，但索力分布较均匀；2段设铰工况下，刚接与铰接间隔交替，铰接处索力增大，刚接处索力减小，但总体分布较均匀且索力在1 000 kN左右变化；3段设铰、4段设铰、6段设铰工况下，铰接处吊索索力增大明显，靠近跨中铰接处的吊索索力最大，最大索力随着设铰数量的减少而不断增大，6段设铰工况下最大吊索索力达到1 803.0 kN，超过吊索正常使用极限值1 584.2 kN，但未超过承载能力极限值；逐渐远离跨中，铰接处吊索索力不断减小；相邻铰接口中间刚接区域的吊索索力与铰接处索力相比大幅下降，其索力总体比全部铰接下索力小。

2.2.5 梁段下缘开口宽度变化规律

设置2个距离很近的节点，观察梁段下缘开口宽度的变化，以开口目前宽度与节点合龙后宽度的差值反映下缘开口宽度变化。不同工况下下缘开口宽度变化见图12、表5。

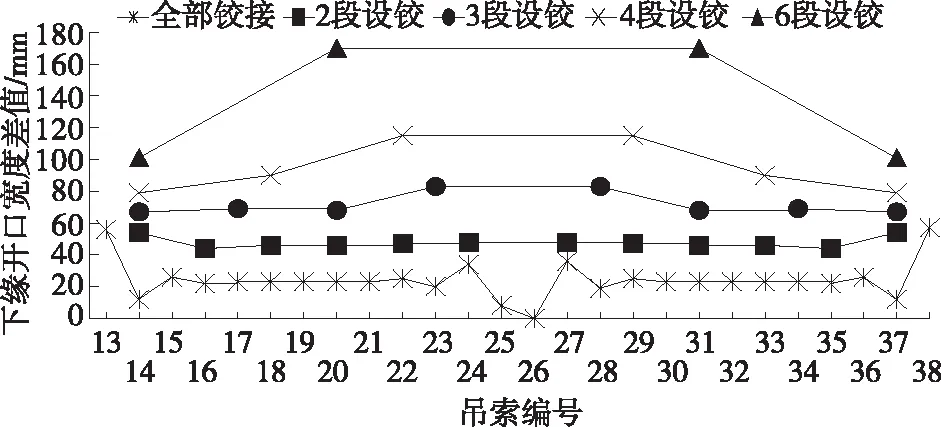
图12 不同设铰工况下下缘开口宽度的变化

表5 不同设铰工况下下缘开口宽度最大差值 mm

由图12、表5可知：梁段下缘开口宽度均大于合龙开口宽度，此阶段加劲梁线形向下凹，开口向两侧扩大。随着设铰数量的减少，下缘开口宽度增大。6段设铰工况下开口宽度最大，最大开口宽度差值达170 mm，最大开口宽度位于跨中；3段设铰、4段设铰、6段设铰工况下，从跨中往两侧，开口宽度减小；全部铰接工况下，除两侧开口宽度略大于2段设铰工况下开口宽度外，下缘开口宽度在所有工况中最小；2段设铰工况下所有位置的开口宽度基本一致，变化很小。

3 主梁节段施工监控分析

该桥实际采用2段设铰施工，相比全部铰接，工期、临时连接件数量均减少一半，同时2段设铰和全部铰接对结构的影响相差不大。与3段设铰、4段设铰、6段设铰相比，2段设铰的临时连接件数量及成本较大。在梁段吊装过程中，吊上即刚接的施工时间相比吊上只安装临时连接长一些，由于3段设铰、4段设铰、6段设铰工况下刚接的梁段增多，其施工时间增大。

全桥设置5个应力提取截面，分别位于1/8L、1/4L、1/2L、3/4L、7/8L处，其中跨中截面测点布置见图13。表6为跨中不同位置应力实测值和理论值对比。由表6可知：实测应力与理论应力的比值为0.6～0.8。考虑到钢桁梁在光照下易产生梯度温度，对钢桁梁的应力量取会产生误差，此阶段钢桁梁受力与理论分析基本相符，满足相关要求。

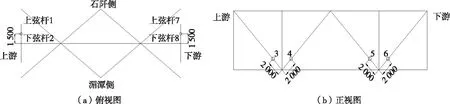
图13 跨中截面应力测点布置(单位：mm)

表6 跨中截面应力实测值、理论值对比

表7为某施工阶段实测索力与理论索力对比。由表7可知：吊索实测索力与理论索力吻合较好，实测索力与理论索力的比值为0.9～1.0，实际索力基本按照理论索力的变化规律变化，整体情况偏好。整体上悬索桥实际施工状态均在控制范围内。

表7 某施工阶段实测索力与理论索力对比

全部铰接工况下加劲梁应力、线形与2段设铰工况下较接近，其梁段受力更稳定，开口宽度更接近合龙状态。但加劲梁采用全部铰接，结构整体刚度较小，抗风能力较弱，不便于平行作业，施工工期较长，在后续梁段刚接时，由于设置的临时连接铰数量较多，会延长工期，并增加加工制作成本，整体经济性较差。多段设铰钢桁梁杆件应力高，临时铰数量减少，桥面板节段可部分焊接成型，节省施工工期，减少临时铰加工制作费用。

4 结论

(1) 随着全桥设铰数量的减少，加劲梁应力显著增大。

(2) 设铰数量对加劲梁线形和主缆线形的影响有限，差别主要出现在跨中部分区域。

(3) 随着设铰数量的减小，吊索索力变化幅度增强，索力分布逐渐不均匀，而且最大索力快速增大，逐渐接近极限临界值。

(4) 随着设铰数量的减少，下缘开口宽度增大，最大开口宽度位置逐渐变化到跨中位置。2段设铰工况下开口宽度较小且分布均衡。

(5) 临时铰用量随着设铰数量的增大而增多，主梁整体工期延长，经济性较差。