一种基于对抗神经网络的方法在钻井数据恢复中的应用

张 宁

（中国石化集团国际石油勘探开发有限公司，北京 100101）

数据缺失是一种常见的现象，如机器学习中的UCI数据集超过40%都有数据缺失[1]。数据缺失将减少样本信息，使有价值的信息被忽略，增加了分析数据的难度，可能会导致数据决策偏差[2]。

目前具有很多填补缺失值的算法。基于统计学的填补方法包括使用均值填充缺失值[3]，使用上一次的观察值来填充缺失值[4]，使用众数来填充缺失值[5]。这些基于统计值的填充方法仅仅考虑了原式数据集的共性，并没有考虑每个样本独立的特性。常见的填补方法可以分为两类：鉴别和生成。鉴别方法包括MICE[6]、MissForest[7]，Matrix Completion[8]；生成法包括基于深度学习的GAN[9-11]。然而目前的生成式填补算法存在着一些缺点，该类方法需要处理的数据满足一定的先验分布，当数据中含有混合类别和连续变量时，其泛化能力就会很差[12-13]。

本文提出一种新颖的缺失数据填补方法，主要构建了一个生成对抗填补网络（简称GAIN）完成填补缺失数据的过程。在GAIN中，生成器的目标是精确填补缺失的数据，判别器的目标是准确地分辨数据是填补的还是真实的。所以判别器要最小化分类误差率，而生成器要最大化判别器的分类误差率，这样两者就处在了一种相互对抗的过程中。同时为了使这个对抗过程得到更加理想的结果，还为判别器提供了关于数据的部分隐含信息，逼迫生成器生成的样本接近于真实的数据分布[12]。

1 符号说明

为了方便后续的公式推导，首先对一些符号进行说明。认为χ:χ=χ1×···×χd是一个d维空间。假设X:X=(X1,···,Xd)是χ的一个随机变量，本文称其为数据向量。假设M:M=(M1···Md)表示取值{0,1}的随机变量，本文将其称为掩模向量。M反映了哪些变量是观察数据，哪些是填补的数据。本文定义一个新空间,i=1,2,···,d，其中*表示不在χ任何一维空间χi中的数据。定义表示新生成的d维空间。定义一个新的随机变量:

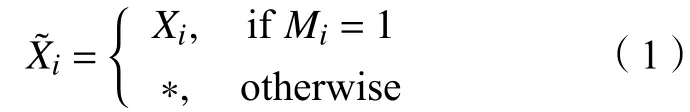
2 生成对抗插补网络（GAIN）

图1展示了本文提出的GAIN网络架构。

2.1 生成器

G将、M和Z作为输入，X¯作为输出。其中Z是一个d维的噪声变量，独立于所有的变量。这一部分与标准的GAN非常的类似，输入噪声变量。本文定义两个随机变量，，如下所示：

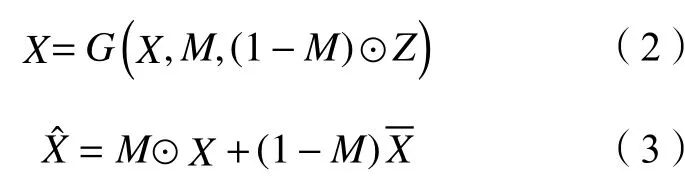
这里⊙表示同位元素相乘；表示填补值的向量，不含已观察到的数据部分，这里需要注意的是，G会为每一部分都输出一个值，即使有些部分不是缺失的；表示填补后完整的数据向量，它观察局部信息，然后用X中的估算值代替对应位置的*得到。

因为M中的值（0,1）指示了数据中哪些部分是缺失的，哪些部分是可以被观察到的。本文使用相同尺寸的单位矩阵与M相减，0和1的位置互换，就显示了哪些部分是需要进行估的，所以在的表达式中(1-M)⊙Z表示了使用随机噪声Z来填补缺失的部分。(1-M)⊙Z代替Z是为了告诉Z在中哪些部分是需要使用噪声进行填充的。

2.2 判断器

这部分将介绍Discriminator (D)，和标准的GAN一样，D被用来作为一个对抗者训练G。但是与标准的GAN中的D存在一些不同。标准G生成的结果要么全是真实的，要么全是假的，D给出的判断结果也要么是真要么是假。GAIN框架中的G生成的结果有些部分是真实的，有些部分是生成的；G也不再是识别整个向量的真假，而是尝试判别哪些部分是真的，哪些部分是生成的。这就相当于预测M中m的值。D的输入是和H，输出是表示每个的成分是观察数据的概率。

2.3 提示机制

提示机制(H)在标准GAN的结构中不存在，也是GAIN结构的核心组成部分。它是一个由用户自己定义的随机变量，强化了G和D的对抗过程。H中的元素h依赖于分布H|M=m，将其输入到D中。根据和H，中的值就反应了它是真实数据的概率。H由于是认为定义的，所以H定义的不同，那么给D的提示信息就不同，从而可以训练出具有多个分布的G，根据D的结果来选择最优的那一个。

2.4 目标

通过最大化正确预测M的概率来训练D，通过最小化D能正确预测M的概率来训练G。与标准GAN类似，评估函数如下：

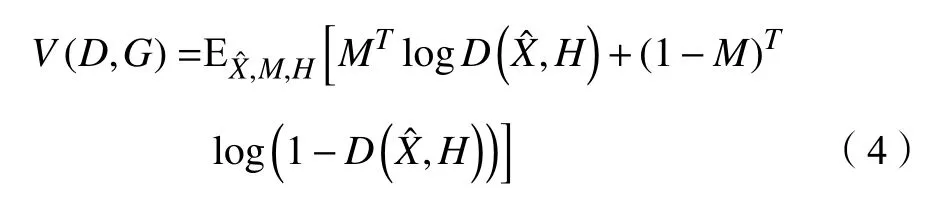
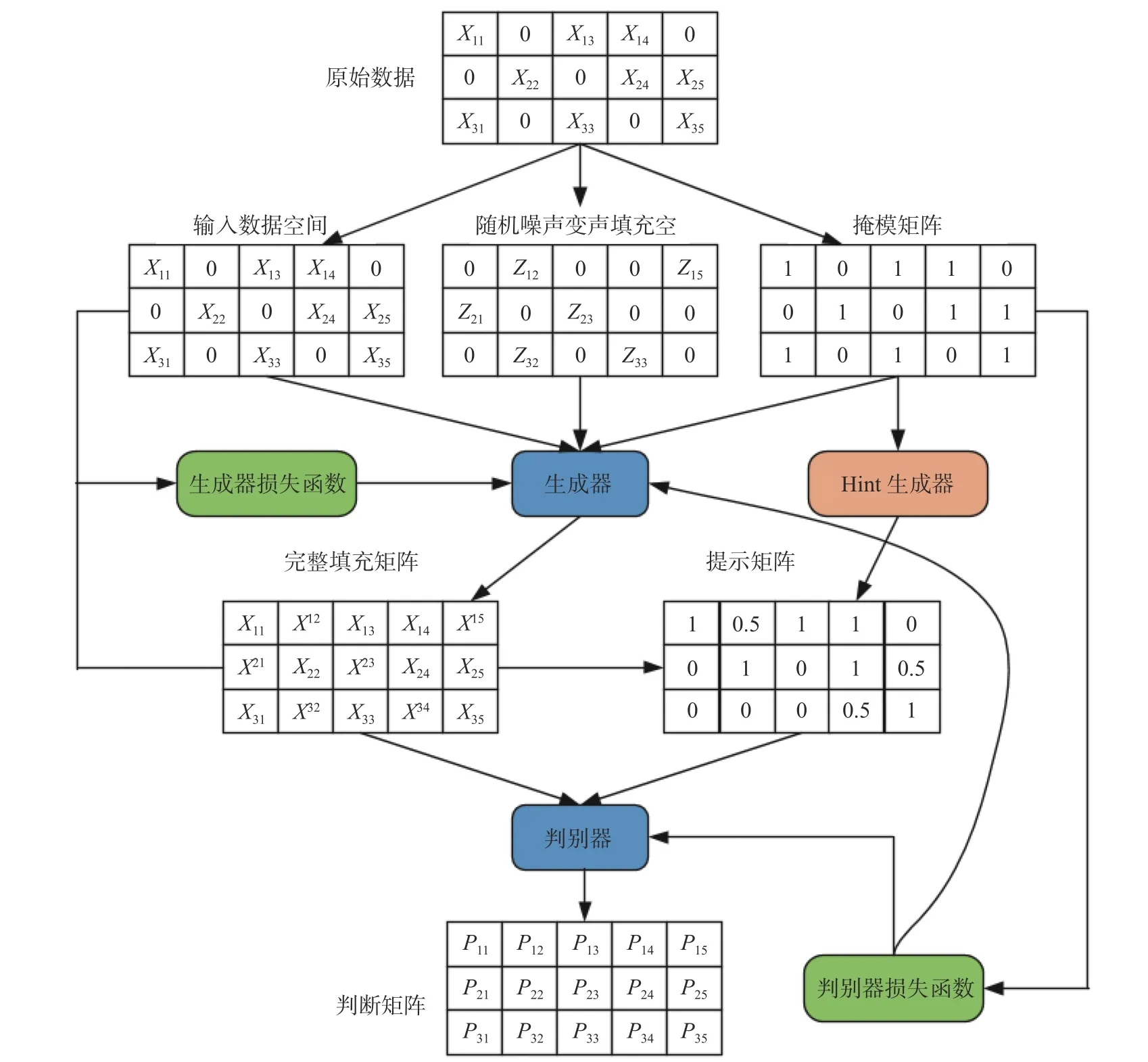
图1 GAIN架构图Fig.1 Structure diagram of GAIN

因此GAIN的目标就是：

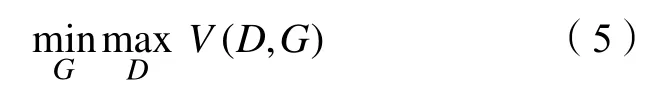
由于对于判别器来说这就是一个简单的二分类问题，所以这里就使用交叉熵来定义损失函数，如下所示：

其中ai表示D预测结果矩阵中的元素，bi表示对应于ai的M中的元素。本文定义，则目标函数就转换成了D能否正确预测M的函数。

3 生成对抗插补网络算法

本文定义随机变量B=(B1,···,Bd)∈{0,1}d，从{1,···,d}均匀随机的采样k个值然后设置：

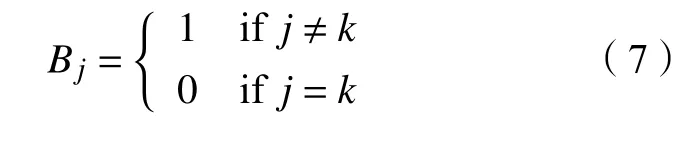
对于给定的M、h的取值为{1,0.5,0}，定义为：

判别器D的训练过程。固定一个G和小批次的kD，首先从数据集中抽样kD个样本x˜(j)和对应的m(j)，从Z和B中抽样kD个样本z(j)和b(j)，然后根据公式计算xˆ(j)和h(j)。当G固定的时候，D的唯一输出就是对应于每个样本的bi=0的部分，定义关于D的损失函数：

D根据以下的准则来训练：

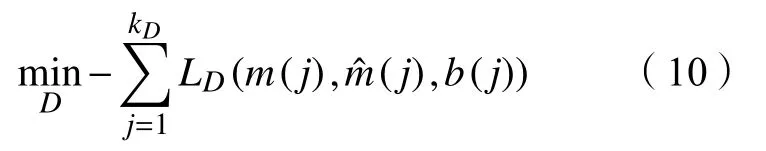
生成器G的训练过程。使用最新训练过的D，以小批次的kG来进行训练。G实际上输出是一个包含所有数据的向量，因此在G的训练过程中，本文不仅要使缺失地方（mi=0）填补的值成功骗过D，还要保证真实被观察的数据(mi=1)的输出也要接近真实值。于是本文定义两个损失函数，第一个损失函数LG:{0,1}d×[0,1]d×{0,1}d→R如下所示：

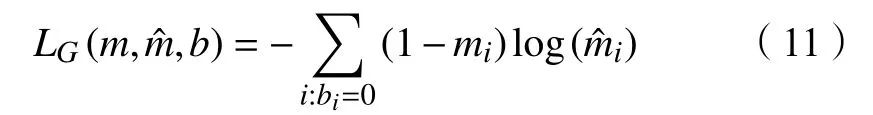
LG用来描述数据缺失的部分(mi=0)，它用来评估填补的质量，它的值越小，表示mi=0被D判别为mi=1的概率越接近1。

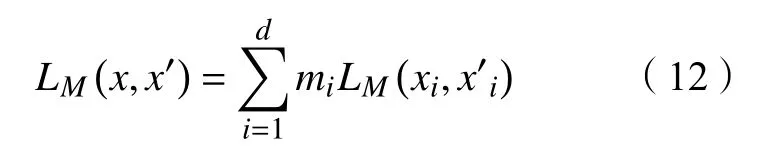
其中

LM用来描述数据观察的部分(mi=1)表示重建误差，用来评估真实观察值经过G的输出与真实值的差距。它的值越小，说明重构后的值越接近真实值。因此，本文可以使用一个完整的损失函数评估训练过程：

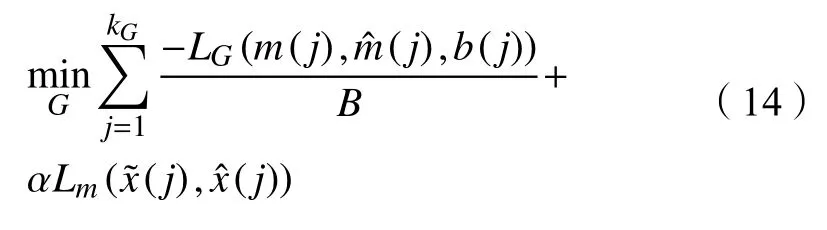
其中α 是一个超参数。

4 实验

在本节中，本文将使用公开数据集和真实数据集验证GAIN的填补性能。首先，本文使用4种公开UCI数据集来验证GAIN的性能。进一步地，本文使用来自石油行业的真实钻井液数据集来验证GAIN方法的有效性。

本文每个实验进行10次，在每个实验中使用10折交叉验证，分类准确率作为性能指标。分类准确率A定义为：

式中：P为被模型预测为正的正样本；Q为被模型预测为负的负样本；R为被模型预测为负的正样本；S为被模型预测为正的负样本。

4.1 UCI数据集

本文使用4个UCI公共机器学习数据集 （Falre、Abalone、WineQuality、CMC）分别来验证GAIN的填补性能。首先，将数据集随机选取30%设置为缺失值（用0表示缺失值），之后将该数据集平分为数据集A和数据集B。然后，将数据集A分为训练集（70%）和测试集（30%）来训练模型，模型训练完毕过后，将带缺失值的数据集B使用GAIN进行填补，生成填补数据集C，最后，使用分类算法在填补数据集C和带缺失的数据集B上验证填补效果，分类方法选用LightGBM和XGBoost。

本节实验过程为：每个实验做10次，每次使用10折交叉验证，将10次实验的平均值作为最后的分类结果，使用GAIN方法填补后的数据集与填补前的数据集在分类任务上的性能对比分别见表1和表2所示。从表1和表2可以看出使用GAIN填补数据过后分类精度都得到了提升。

各个数据集在不同的缺失率的填补性能见图2和图3。在Falre、Abalone、WineQuality、CMC这4个数据集的不同数据缺失率的情况下，经过填补过后的数据使用LightGBM和XGBoost两个方法进行分类。虚线为使用GAIN填补过后的数据进行分类的结果，实线为缺失数据进行分类的结果。

从图3可以看出使用GAIN填补过后的数据，比直接使用带有缺失值的数据做分类精度更好。

本节实验将与当前流行的缺失值填补算法MICE[6]、MissForest[7]、Matrix[14]、EM[15]相比较，来验证本文提出的算法的有效性，分类算法使用XGBoost，每个数据集的缺失率设置为30%。见表3所示，本文提出的算法在不同的数据集上分类效果更好，验证了本文所提算法的有效性。

表1 分类任务的精度对比（LightGBM）Table1 Accuracy comparison of classification tasks(LightGBM)

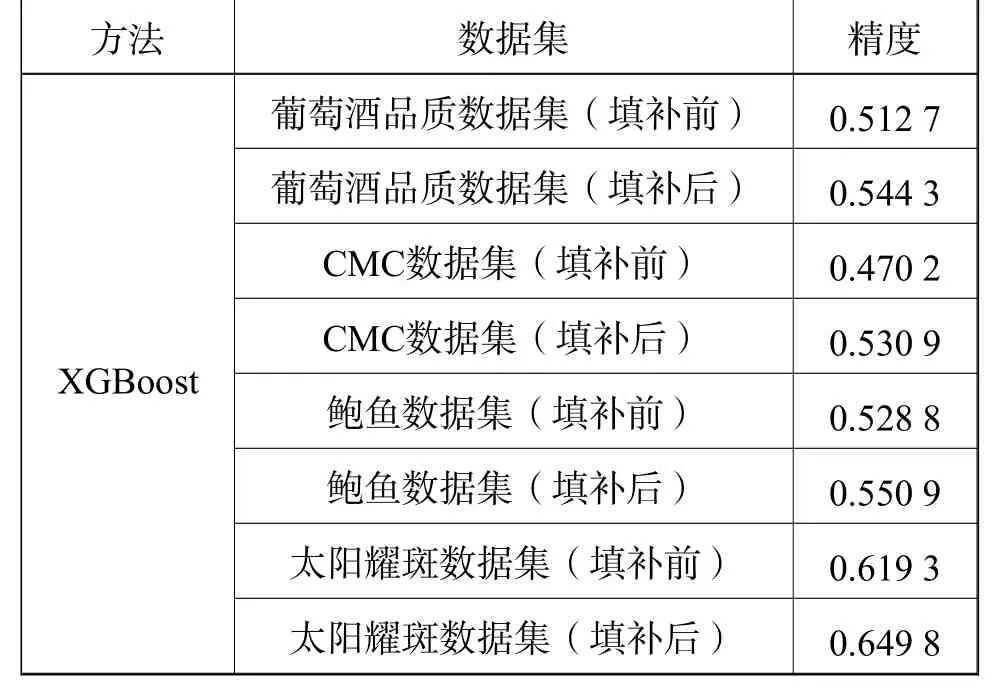
表2 分类任务的精度对比（XGBoost）Table2 Accuracy comparison of classification tasks(XGBoost)

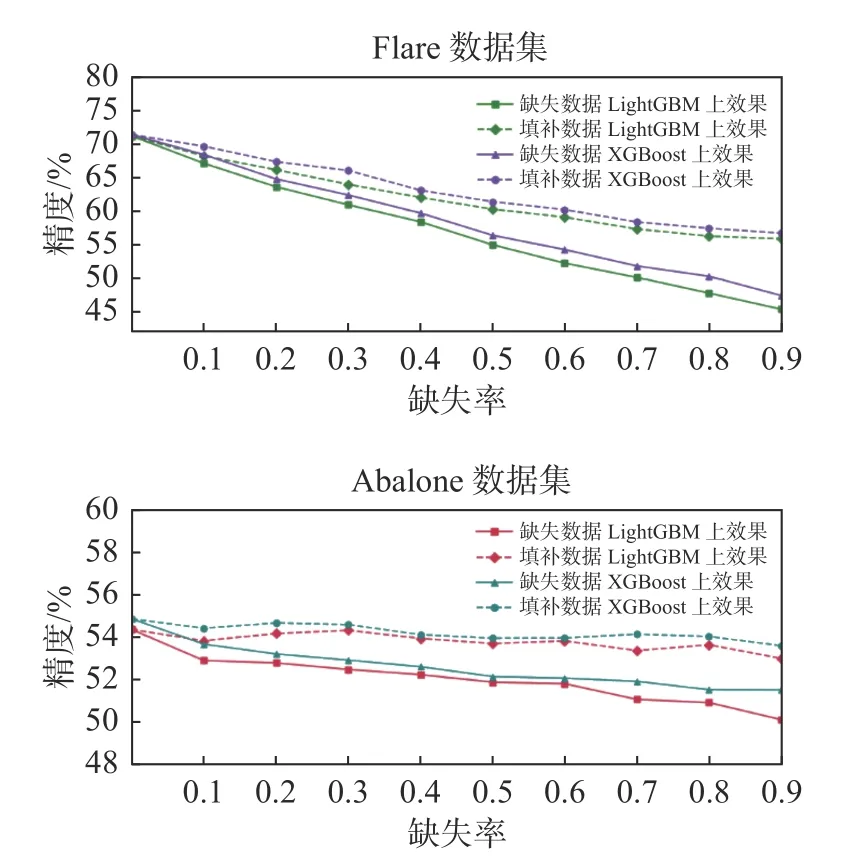
图2 不同缺失率的分类性能Fig.2 Classification performance with different missing ratios

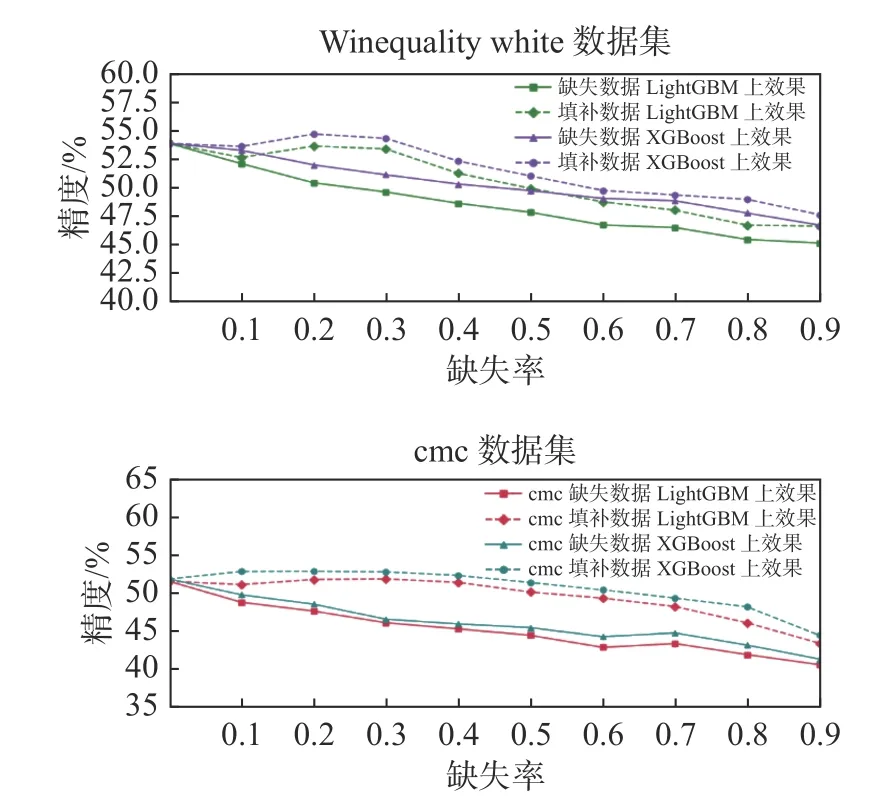
图3 不同缺失率的分类效果Fig.3 Classification performance with different missing ratios

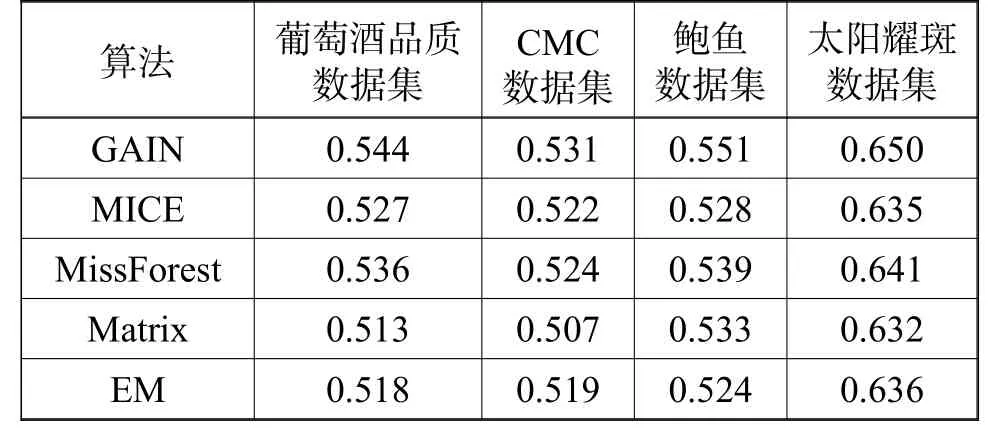
表3 不同填补算法的精度对比Table3 Accuracy comparison with other methods

4.2 真实钻井液数据集

本节在真实钻井液数据集上验证GAIN的有效性，该数据集收集有2 000个钻井液体系使用案例，这些案例中涵盖32种钻井液体系，数据集的缺失率设置为30%，实验目的是验证GAIN在该数据集上的钻井液体系分类精度。本节选用了主流的四种分类方法：LightGBM、XGBoost、SVM和BP神经网络。本节实验过程为：每个实验做10次，每次使用10折交叉验证，将10次实验的平均值作为最后的分类结果，四种分类方法的平均精度见表4所示。

从图4可以看出使用GAIN填补过后钻井液数据在四种分类方法的平均精度比未经过GAIN填补的都好，精度在LightGBM、XGBoost、SVM和BP神经网络上分别提升了1.42%、1.03%、0.29%和1.88%。实验结果也表明GAIN方法在真实钻井液数据集上同样有效，具备一定的普适性和实际应用价值。

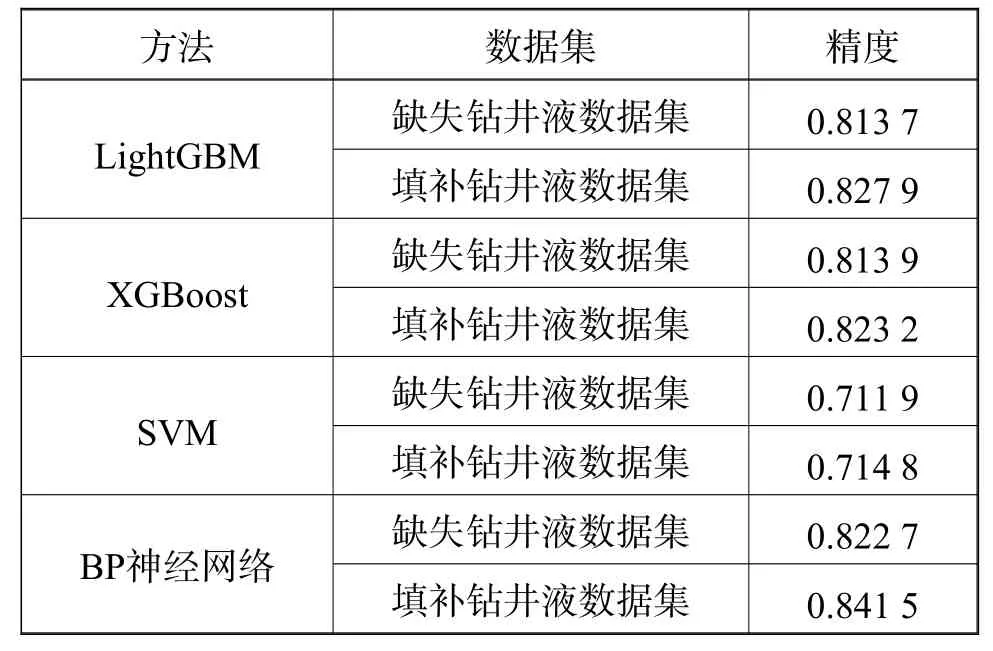
表4 在真实钻井液数据集分类任务的精度对比Table4 Accuracy comparison of classification tasks on real drilling fluid datasets

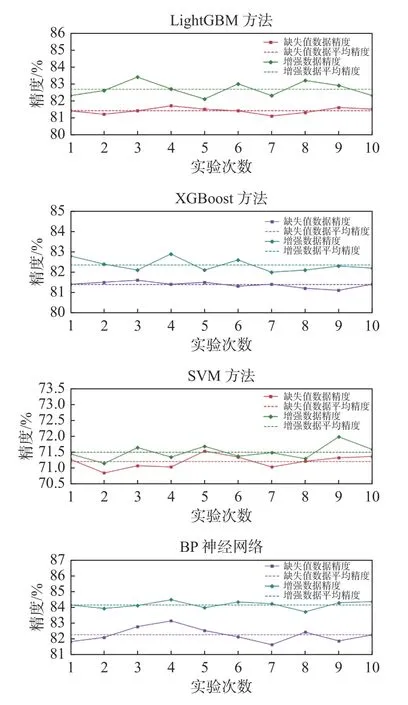
图4 不同缺失率在钻井液数据集上的分类效果Fig.4 Classification performance with different missing ratios of drilling fluid datasets

本节实验将与当前流行的缺失值填补算法MICE、MissForest、Matrix、EM相比较，来验证本文提出的算法的有效性，分类算法使用XGBoost （表5），GAIN在钻井液数据集上效果依旧是最好的，表明本文的算法的有效性。

表5 不同填补算法的精度对比Table5 Accuracy comparison with other methods on real drilling fluid datasets

5 结语

数据缺失是一种很普遍的现象，有时数据本身就很难获取，有的由于采集设备的不稳定性或者被干扰等原因，采集到的数据往往是不完整的，而数据的缺失部分则阻碍了对数据的深入分析，由此带来数据决策偏差等问题。本文提出基于一种生成对抗填补网络方法来对缺失数据进行填补。公开数据集和真实数据集上的实验结果验证了本文方法的有效性，在公开UCI数据集和真实钻井液数据集上性能良好，显著优于填补前的数据集。基于本文方法开发了石油领域应用软件，展示了本文方法具备一定的推广应用价值。