基于MTMD 系统的弧形钢闸门减振分析
苏聪聪,吴泽玉,王 俊
(1.许昌学院 土木工程学院,河南 许昌 461000; 2.华北水利水电大学 土木与交通学院,河南 郑州 450045)
弧形钢闸门以其轻盈的结构形式、合理的受力性能以及启闭力小等优点,在水利工程中得到广泛应用。但是弧形钢闸门的流激振动问题较为突出,其因流激振动而造成破坏在国内外时有发生[1-3]。 闸门流激振动由水动力荷载特点和闸门振动特性决定,当水动力荷载无法改变时,优化闸门的动力特性成为唯一选择。纵观弧形闸门的破坏性态,大部分是支臂发生过大振动,造成支臂动力失稳,导致荷载效应超过材料强度,进而发生破坏。 调谐质量阻尼器(TMD)减振效果对结构固有频率波动敏感,而钢闸门一般在水下工作,自振频率受流体质量的影响,故TMD 减震效果较差。 为了克服TMD 系统缺点,增强其鲁棒性,Clark 提出将一个大的TMD 分成具有分布频率的多个小TMD 系统,即多阻尼调谐质量阻尼器(MTMD)减振系统,而金鑫等[4]、王智丰等[5]和孟庆成等[6]利用MTMD 分别成功解决了漂浮式风力机、大跨胶合木拱桥和高架候车厅的过大振动问题。 通过将MTMD 系统中各TMD 并联,再施加于减振结构上,分析表明MTMD 明显优于TMD 系统,扩大了调谐质量阻尼器的应用范围。
本文首先推导MTMD 系统动力学方程式,给出被控结构动力放大系数计算式,以纠正相关论文中动力放大系数计算式不正确问题[7-9];然后以动力放大系数为工具确定闸门合理MTMD 频带宽度、阻尼比和TMD 数量等参数;最后研究设置合理MTMD 参数情况下,弧形钢闸门因流激荷载而引起的振动响应,分析MTMD 的减振效果。
1 闸门-MTMD 系统运动微分方程和动力放大系数公式推导
弧形钢闸门模型选自文献[10]中实体结构,有限元网格如图1 所示。
闸门纵横梁采用空间梁单元,闸门面板选用壳单元,吊杆采用空间杆单元。 利用Westergaard 法考虑流体对结构动力特性的影响。 闸门模态分析表明,第一阶振型质量参与系数为81%,MTMD 系统振动控制以抑制第一阶振动为主,故将闸门等效简化为单自由度结构系统进行MTMD 减振分析,而第k个TMD 的动力方程为
式中:mk、ck和kk分别为第k个TMD 系统的质量、阻尼和刚度;x··k、x·k和xk分别为第k个TMD 系统的加速度、速度和位移;x·s和xs分别为闸门的速度和位移。
设流激荷载f(t) 作用于闸门上,被控闸门简化为单自由度动力学方程:
式中:ms、cs和ks分别为闸门的质量、阻尼和刚度;s为闸门的加速度。
闸门-MTMD 动力学方程的矩阵表达式为
式中:X、、为位移、速度、加速度列向量;F为荷载列向量。
质量矩阵M为
阻尼矩阵C为
刚度矩阵K为
设闸门所受荷载为简谐激振力f(t)=F0eiωt(ω为圆频率) ,求解式(3)得到闸门-MTMD 系统的动力放大系数为
其中
式中:μk、γk、ζk、ζs、λ分别为第k个TMD 质量比、频率比、阻尼比、被控结构阻尼比、激励力圆频率与被控结构自振圆频率之比,μk=
、ζk=,ωk、ωs分别为激励力圆频率和被控结构自振圆频率。
2 弧形钢闸门MTMD 系统参数的确定
一般情况下,MTMD 质量取被控模态质量的1%~5%,本例按被控模态质量比2%确定阻尼器质量。MTMD 参数包括频带宽度、阻尼比和TMD 数量等,下面分别进行讨论。
2.1 频带宽度影响
为了研究方便,引入以下变量:n个TMD 固有频率的平均值f0,f0=fk/n;频带宽度ΔR, ΔR =。
假定MTMD 阻尼比为5%;考虑到闸门有两对支臂(4 根梁),加之为了保证以被控结构频率为中心确定MTMD 中TMD 数量,初步按9 个TMD 设计。 计及流体对闸门动力特性的影响,以闸门淹没一半所得结构基频为结构被控频率。 动力放大系数D随ΔR、ω/ωs连续变化的三维图如图2 所示,频带宽度对D的影响如图3 所示。
由图2 和图3 可知:频带宽度ΔR =0 即单个TMD系统在被控频率上控制效果最好;但被控频带很窄,两旁有两个很高的次波。 当频带宽度逐渐增大时,在被控频率上抑制效果逐渐变差;而偏离被控结构频率,动力放大系数在被控频率两边峰值消失,控制范围增大,控制效果变差,故MTMD 以牺牲控制效果来提高阻尼器的鲁棒性。 频带宽度ΔR =0.20 时,可得到较好的振动控制效果。
2.2 阻尼比影响
为了讨论MTMD 的阻尼比对闸门振动控制效果的影响,假定阻尼器的个数为9 个,频带宽度取ΔR =0.20。 阻尼比ζk取值范围为2%~10%,分析MTMD 阻尼比对动力放大系数D的影响。 动力放大系数D随阻尼比ζk和ω/ωs连续变化三维图如图4 所示,阻尼比ζk对动力放大系数D的影响如图5 所示。
由图4、图5 可知:MTMD 阻尼比较小时,在被控频率周围小范围内有较好的抑制振动响应的作用,但偏离这个范围时结构产生类似于单TMD 的高峰值次波。 随着MTMD 阻尼比的增大,次波逐渐减少,D—ω/ωs曲线变得越来越光滑,对结构控制效果也越来越好。 当MTMD 阻尼比过大时,次波完全消失,阻尼器的振动控制效果大大降低。 原因是MTMD 阻尼比过大,阻尼器的共振反应降低,不能耗散被控结构更多的振动能量。ζk=0.05 时,闸门振动控制效果较好。
2.3 TMD 数量影响
频带宽度取ΔR =0.20,阻尼比ζk=0.05,研究MTMD 系统中TMD 数量n对被控结构抑振效果的影响,分析TMD 数量对动力放大系数D的影响。D随TMD 数量和ω/ωs连续变化三维图如图6 所示,TMD数量对D的影响如图7 所示。
由图6、图7 可知,在MTMD 频带宽度、阻尼比和质量比固定的情况下,单一TMD 在被控频率上抑振效果最好,但偏离此频率会出现较大的次波,此结论验证了频带宽度ΔR =0 控制效果最好的结论。 当n大于5时,抑振效果差异不大。 考虑到闸门两对支臂共4 根受力梁,加之以闸门被控基频为中心确定TMD 数量,初步设计为9 个。
3 弧形钢闸门MTMD 系统减振控制
选用图1 弧形钢闸门,设置多调谐质量阻尼器进行动力荷载效应分析。 对本实例弧形钢闸门进行模态分析,受控弧形钢闸门第一阶模态质量为315 000 kg;MTMD 质量比和阻尼比分别按2%和5%设计;频带宽度和阻尼器数量分别取0.20 和9 个。 MTMD 中TMD质量相同,频率变化通过改变阻尼器刚度实现,9 个TMD 结构参数见表1。 分析弧形钢闸门模态应变能可知,闸门支臂的模态应变能最大,加之对既有闸门破坏情况分析发现,因支臂动力失稳而导致闸门破坏的案例比比皆是,因此确保支臂安全是防止闸门破坏的主要手段。 由支臂最大模态位移确定合理MTMD 的安装位置。
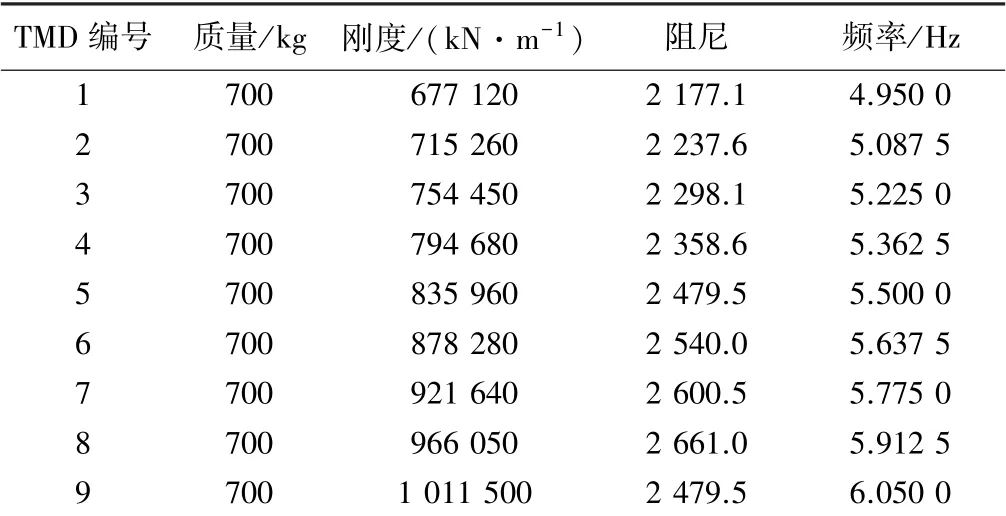
表1 MTMD 系统参数
实测闸门流激荷载压力时程曲线如图8 所示,按三角形加载形式施加于弧形钢闸门上游面。 动力时程求解方法选用钟万勰教授提出的精细积分法[11-12],得到闸门设置MTMD 前后支臂3/4 跨位移和速度响应曲线,如图9、图10 所示。 可知,闸门设置MTMD 能有效降低结构因流激荷载而引起的位移和速度响应值。由图9 可知,最大位移降低幅度为58%,平均位移降幅为49%。 由图10 可知,最大速度降低幅度为67%,平均速度降幅为56%。 因此,MTMD 可有效降低弧形钢闸门流激振动响应。
4 结 论
通过研究弧形钢闸门因流激荷载而引起的振动效应,依据实测的闸门流激荷载压力值,确定了合理MTMD 频带宽度、阻尼比和阻尼器的数量,对设置MTMD 的闸门进行动力时程分析,得到以下主要结论:①合理MTMD 频带宽度不仅能有效提高MTMD 的频率控制范围,而且可迅速降低结构因流激荷载而引起的动力响应;②MTMD 的阻尼比不能过大也不能过小,合理的阻尼比对降低结构的动力响应至关重要;③MTMD中TMD 安装位置和数量直接影响阻尼器的控制效果,确定TMD 数量时要考虑实际结构的受力性能;④闸门设置MTMD 可快速降低因流激荷载而引起的位移和速度响应值,保证闸门安全运行,MTMD 减振系统可推广至类似水利工程。 本例建议模态质量比2%,TMD 数量9 个,TMD 阻尼比ζk=0.05,ΔR =0.20。

