一种基于正弦波高精度互模糊函数的通信卫星干扰定位技术
陈 昊,赵 斐
(北京跟踪与通信技术研究所,北京 100094)
0 引言
通信卫星系统以其覆盖范围广、易接入、不受地形影响的特点为信息化条件下联合作战中指挥、侦察诸单元的广域连接创造了便利的条件,在军事通信领域占据越来越重要的地位,是保障战略、战术通信的重要手段[1-2]。由于通信卫星处于开放的空间,电磁环境极其复杂,容易遭受敌方恶意干扰、地面无意干扰和非法使用,同时还包括由于空间频率复用引入的自干扰和互干扰,这些干扰和盗用严重制约着通信卫星系统效能的发挥。虽然卫星通信系统的自干扰和互干扰可以通过系统参数和资源的调配进行规避,但地面系统的干扰、盗用、敌方的恶意干扰需要定位干扰源,通过协调、稽查和摧毁等手段完成干扰源的消除。
目前,基于卫星平台的干扰源定位体制主要有以下几种: 1)基于单星实现定位。单星实现测向定位的主要原理是利用单个运动卫星在某个位置测得目标AOA信息,然后通过一定的定位算法确定目标干扰源的位置[3]。利用单星测向定位法进行定位的定位误差对测向误差敏感。测向误差越大则定位误差随之越大,距离星下点越远则测向误差引起的定位误差越大;在星下点附近,卫星轨道越低,定位误差越小,所以低轨卫星有利于定位精度的提高。此方法需在卫星平台的一个基准平面上配置3根全向天线,构成一个基线相互垂直的二维相位干涉仪;但是对于通信卫星来讲,安装星载测向设备并不太实际。2)基于双星实现定位。双星定位体制是目前卫星干扰源定位的主要体制,该体制利用干扰源信号到达时差(TDOA)以及到达频差(FDOA)为定位参数,实现干扰源的无源定位,参数估计主要原理是利用各路干扰源信号的相关性,主要采用互模糊函数算法(cross ambiguity function,CAF)对定位参数进行估计[4-5]。这种方法只需接收到转发干扰源信号即能定位,不需要特殊的卫星载荷设备,不需要知道信号调制等特征信息,且能对大范围进行连续不间断侦察。但CAF算法通过二维峰值搜索得到TDOA和FDOA的估计值,存在计算量大、搜索时间长、精度较低等缺点。
本文在CAF算法的基础上,提出了一种基于正弦波高精度互模糊函数频差估计方法,并针对利用两颗静止通信卫星实现干扰定位时主信号和辅助信号信噪比差异大、辅助信号微弱的问题,采用改进的互模糊度函数实现双星TDOA和FDOA的测量,实现对干扰信号的定位,为战场决策和系统资源管理提供有力支撑。
1 算法原理
1.1 基本原理
根据通信卫星地面系统干扰检测与识别结果,在条件允许的情况下可以启动双星协同的干扰源定位,实现干扰源位置的确定,并依据识别的干扰参数,结合电磁环境的计算,评估不同空间、时间、频率下卫星通信系统受干扰的程度,实现干扰的体系化管理。定位方法如图1所示。
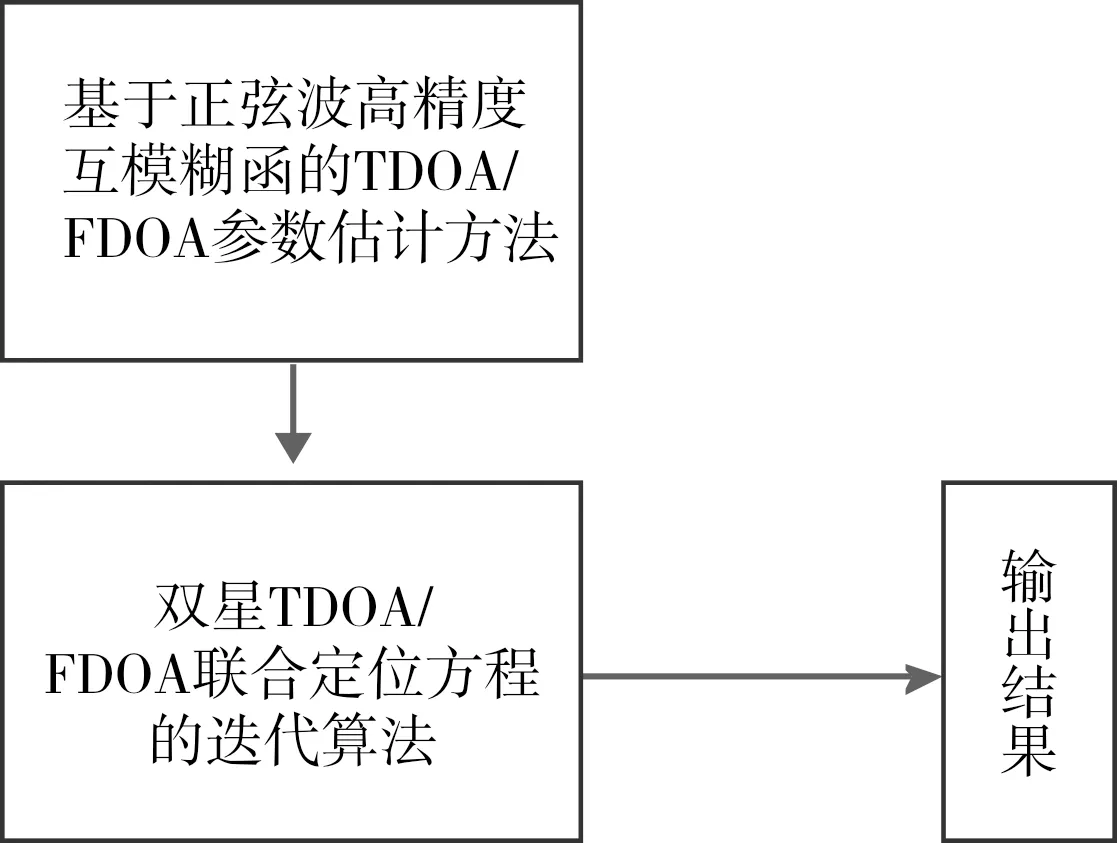
图1 基本过程Fig.1 Basic process
位于空间的受干扰主星和M-1(M≥2)颗相邻卫星透明转发地面干扰源信号,由地面站接收卫星转发信号间的TDOA与FDOA可以计算出卫星上行信号间的TDOA与FDOA值。利用卫星上行信号TDOA值可以确定一个等TDOA单叶双曲面,而卫星上行信号FDOA值可以确定一个等FDOA类轮胎曲面,同时干扰源位置的约束条件(如干扰源位于地球表面)也会确定一个曲面,以上各曲面的交点即干扰源的估计位置。这里以双星TDOA/FDOA定位系统为例,对其原理进行说明[6-7]。双星TDOA/FDOA联合定位的原理如图2所示。

图2 双星TDOA/FDOA联合定位的原理Fig.2 Principle of TDOA/FDOA joint location with two satellites
图2(a)中,观测卫星S1受到地面干扰源有意或无意的射频干扰,此时卫星S1附近有相邻卫星S2,两颗卫星透明转发干扰源信号。地面接收站和参考站接收卫星S1与S2所转发的干扰源信号,通过参数估计和初步计算可得到干扰源信号到达卫星的TDOA和FDOA值。地面等TDOA曲线与等FDOA曲线的交点即为干扰源的估计位置,如图2(b)所示[8]。
1.2 基于正弦波高精度互模糊函数的参数估计
为了便于分析,设地面接收站收到的受干扰主星和相邻卫星的信号为两个单一频率复正弦波信号:s1(t)=a·exp[j(2πf1(t+τ1)+Φ1)]+n1(t1),s2(t)=b·exp[j(2πf2(t+τ2)+Φ2)]+n2(t2)。其中,a,b表示信号的幅度,f1、f2表示两个信号的频率,Φ1、Φ2分别是信号的初相,在[-2π,2π]随机分布,n1(t1)、n2(t2)表示平稳、零均值的高斯白噪声。设两个信号的记录时间都为T,总的采样点数为N。则D=|τ1-τ2|为需要估计的到达时间差参数,而Δf=|f1-f2|为需要估计的FDOA参数。
根据四阶累积量的定义,可以得出地面接收的信号s1(t)与s2(t)的四阶累积量如式(1)所示,其中“*”表示取共轭。
(1)
由于式(1)的计算量非常大,为了便于计算,可以消除式(1)中的数学期望运算符号E(·),从而可以获得四阶瞬时值。如式(2)所示,可以对FDOA/TDOA进行估计。

(2)
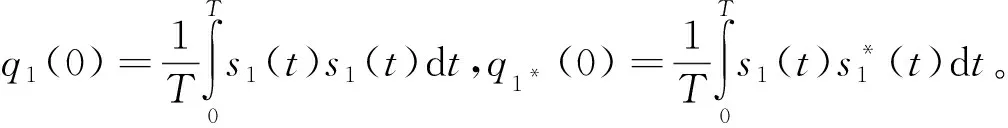
计算在时域搜索范围内[-P,P],当n∈τ(τ∈[-P,P])时,四阶累积量的计算方法如式(3)所示:
(3)
其中k∈[1,N],N为信号采样点数。从而,对式(3)进行快速傅里叶变换即可获得CAFFOS(D,Δf)。如式(4)所示:
(4)
(5)

则可得式(6):
y(t)=exp[j(2π(f1-f2)(t-τ1)+Φ1-Φ2)]
(6)
记f0=f1-f2,Φ0=Φ1-Φ2,因为τ1为常数,所以可以忽略其对频差估计的影响,记t=t+τ1。可以得出包含频差的信号y(t)=exp[j(2πf0t+Φ0)]。设信号的记录时间为T,对信号进行N点的采样得到y(n)=exp[j(2πf0Tn/N+Φ0)],n=0,1,2,…,N-1。
把信号分为两个长度均为N/2的信号y1(n)和y2(n),对应原信号的前N/2点与后N/2点。y1(n)=exp[j(2πf0Tn/N+Φ0)],n=0,1,2,…,N/2-1,y2(n)=y1(n)exp[jπf0T],n=0,1,2,…,N/2-1。

依据推导分析,可知相位的均方根误差为:
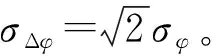
因为fδ=δ·Δf,所以fδ的均方根误差为:
为了评估算法的性能,这里进行了计算机仿真。在仅用四阶互模糊函数的情况下,当N=1024个点,频差f0=21Hz,信噪比10dB时,对原信号加blackman窗后,四阶互模糊函数仿真如图3所示。

图3 四阶互模糊函数仿真图形Fig.3 Simulation graph of fourth-order mutual ambiguity function
按照基于互模糊度的定位算法实现流程,这里首先估计出TDOA,在TDOA确定之后,利用文中提到的高精度四阶互模糊函进一步对FDOA进行估计,其中频差f0=(10+0.25)Δf,相对频偏δ=0.25Hz。进行1000次Monte Carlo仿真,均方根误差如图4所示。
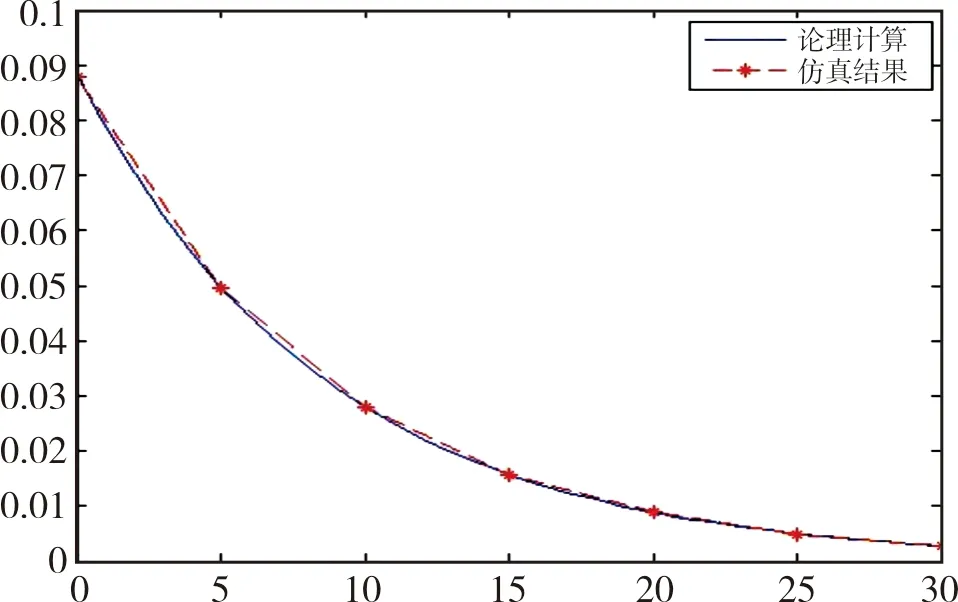
图4 CAF-FOS内插值法的FDOA MSE(频差均方根误差)Fig.4 FDOA MSE(mean square error of frequency difference) of CAF-FOS interpolation method
依据仿真,在信噪比5dB,数据长度为1024的情况下,FDOA估计均方根误差降低为传统CAF-FOS直接均方根误差的2%,估计精度提高50倍。
1.3 基于改进的互模糊函数的干扰源定位算法
通过基于改进的正弦波高精度互模糊函数的TDOA/FDOA参数估计方法得到TDOA/FDOA参数,带入TDOA/FDOA联合定位方程中,根据双星TDOA/FDOA联合定位方程的迭代算法最后获得定位结果。具体过程如下:
由式(17)和(18)可以看出,在蜂窝夹芯基本结构参数相同的条件下,双壁厚类方形蜂窝夹芯的面内等效剪切模量、面外刚度以及等效密度均比等壁厚类方形蜂窝夹芯大。
设干扰源在ECEF坐标系下的位置矢量为u=[xyz]T,接收站和参考站的位置矢量为uj=[xj

图5 卫星转发信号各路径时延与多普勒频移示意图Fig.5 Schematic diagram of delay and Doppler frequency shift for each path of satellite transmitted signal

(7)
图5中Δfc、Δfd、Δfe与Δff可通过式(8)计算:
(8)
式(7)、式(8)中,c为信号传播速度,fc为干扰源信号载波频率。需指出,为方便分析计算,这里假设卫星透明转发信号时,不改变信号的频率。
地面接收站与参考站对接收到的卫星S1与S2透明转发信号进行处理,分别得到两颗卫星转发干扰源信号的TDOA值D1与D2和FDOA值ΔF1与ΔF2。其中,D1与D2满足式(9)所示关系:
(9)
而ΔF1与ΔF2满足式(10)所示的关系式。
(10)
由于D1、D2、τc、τd、τe、τf以及ΔF1、ΔF2、Δfc、Δfd、Δfe、Δff均为已知量,则卫星s1与s2之间的上行信号间的TDOA值ΔT12=τb-τa和FDOA值ΔF12=Δfb-Δfa可将上述已知量代入式中求得。则TDOA/FDOA的联合定位方程如式(11)所示,其中,c为信号传播速度,fc为干扰源信号载波频率。
(11)

(12)

(13)
则此时的(x(N),y(N),z(N)),N为迭代次数,最终估计结果为干扰源位置。
2 仿真试验
为验证本文算法有效性,在Inmarsat卫星通信系统中选取两颗相邻卫星,其星历如表1所列,干扰源位于广州(东经113.3°,北纬23.1°),干扰源信号频率为1.6GHz,地面接收站位于北京(东经116.4°,北纬39.9°),设TDOA/FDOA测量时刻为1 Jul 2011 12:00:00.000,经过计算,卫星、干扰源及地面接收站该时刻在ECEF坐标系中的位置矢量如表1所列,卫星的速度矢量如表2所列[9-10]。由表1和表2可知,地面接收站接收两颗卫星透明转发干扰源信号的上行TDOA值为3.0149ms,上行FDOA值为18.2520Hz。DOA测量时刻卫星在ECEF坐标系下的速度矢量如表3所列。

表1 选中的Inmarsat卫星的星历(1 Jul 2011 12:00:00.000)Tab.1 Ephemeris of the selected Inmarsat satellite(1 Jul 2011 12:00:00.000)

表2 FDOA测量时刻卫星、干扰源及地面接收站在ECEF坐标系下位置矢量Tab.2 Position vector of satellite, jamming source and ground receiving station in ECEF coordinate system at FDOA measurement time

表3 DOA测量时刻卫星在ECEF坐标系下的速度矢量Tab.3 The velocity vector of the satellite in the ECEF coordinate system at the time of DOA measurement

表4 σ不同取值情况下各算法的RMSE/kmTab.4 σ RMSE of each algorithm under RMSE/km of different values
为了更直观地呈现算法的性能,下面给出了卫星高度为35790km,不同固定场景下的定位精度结果。
1)场景一为频率误差0.0073Hz,时差50ns ,如图6所示。此时中值定位精度为500m。

图6 场景一(频率误差0.0073Hz,时差50ns)Fig.6 Scenario one (frequency error 0.0073Hz, time difference 50ns)
2)场景二为频率误差0.0146Hz,时差50ns,如图7所示。此时中值定位精度为1km。
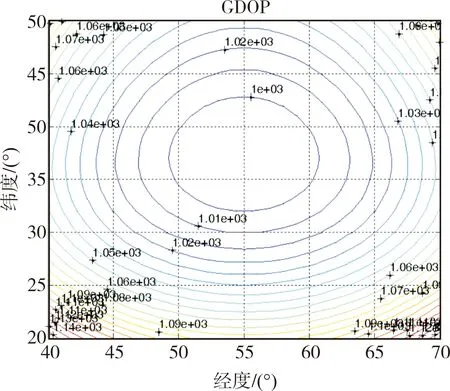
图7 场景二(频率误差0.0146Hz,时差50ns)Fig.7 Scenario two (frequency error 0.0146Hz, time difference 50ns)
3)场景三为频率误差0.0729Hz,时差50ns,如图8所示。此时中值定位精度为5km。
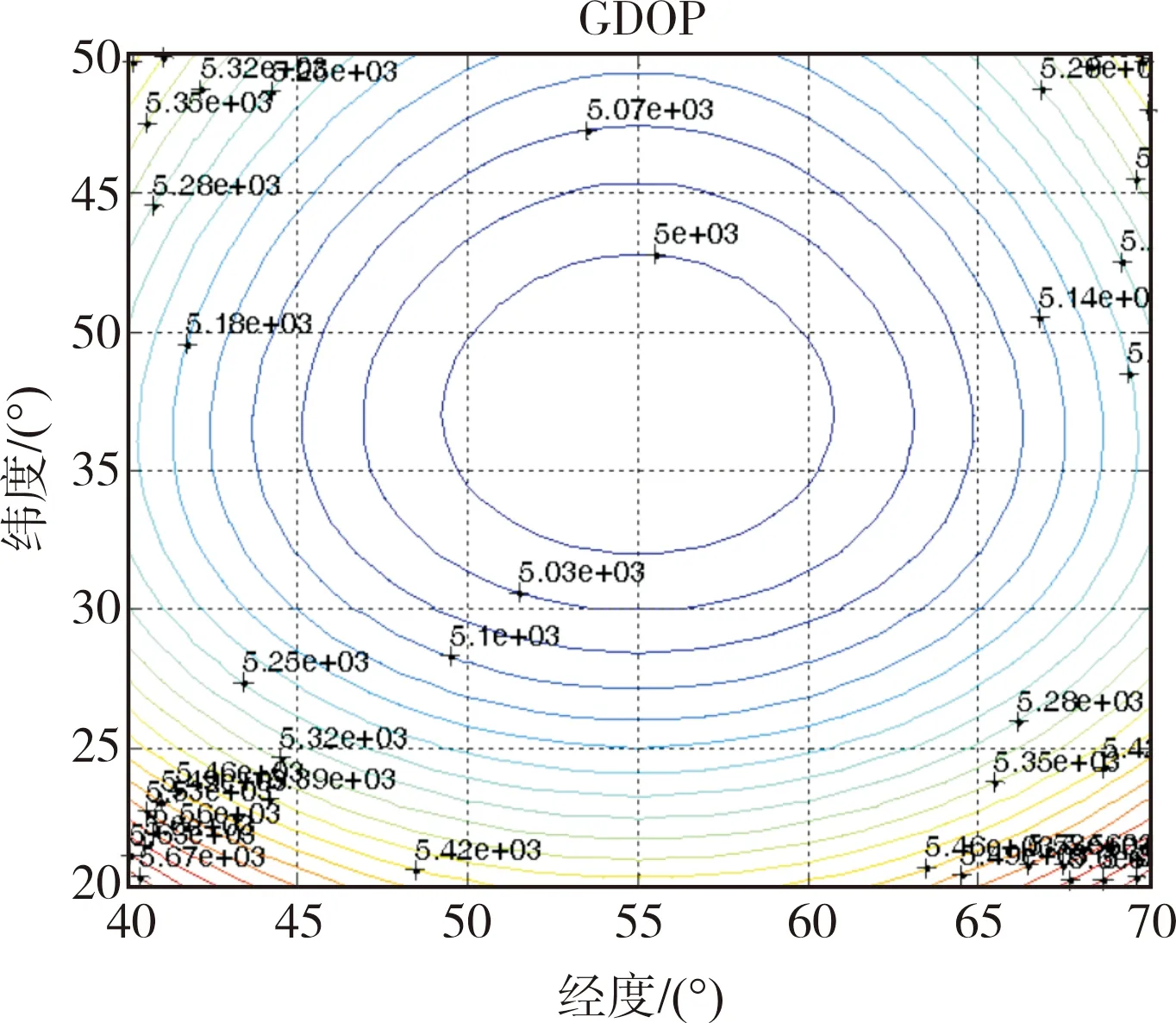
图8 场景三(频率误差0.0729Hz,时差50ns) Fig.8 Scenario three (frequency error 0.0729Hz, time difference 50ns)
4)场景四为频率误差0.146Hz,时差50ns,如图9所示。此时中值定位精度为10km。

图9 场景四(频率误差0.146Hz,时差50ns) Fig.9 scenario four (frequency error 0.146Hz, time difference 50ns)
由仿真结果可知,频率误差越大时,定位精度越低;而当频率误差优于0.01Hz,采用本文提出的算法,干扰定位精度优于1km,相比于其他算法[11],定位精度得到了提升,满足实际系统运行要求。
3 结论
通信卫星系统的干扰信号定位一直是难点问题。本文利用干扰源信号到达时差(TDOA)以及到达频差(FDOA)为定位参数,实现对干扰源的无源定位;同时提出了一种基于正弦波高精度互模糊函数频差估计方法。本文所提出的定位参数估计算法和定位方法,只需接收到转发干扰源信号,不需要知道信号调制等特征信息,并且定位精度高。

