多井干扰下有限导流裂缝井解析试井分析方法

魏 操 程时清 白 江 李宗泽 史文洋 吴嘉鑫，3

（1. 中国石油大学（北京）石油工程学院，北京 102249；2. 延长油田股份有限公司吴起采油厂，陕西吴起 717600；3. 中国航油集团储运有限公司，上海 201100）

0 引 言

目前，对低渗油藏的生产井普遍进行水力压裂，井距较小，特别是二次加密后测试井的压力恢复资料易受邻井生产或注水影响，压力导数曲线在中后期出现“上翘”或“下掉”特征［1-3］。现有试井分析方法常将该特征考虑为受边界的影响［4−5］，导致解释结果失真。此外，常用压裂井试井方法主要将裂缝视为有限导流裂缝［6-11］，求解方法主要为半解析法（Green 源函数法、Newman 乘积原理、Fredholm 型积分、边界元法）和数值法，半解析方法和数值方法可以处理各种复杂储层情况，但计算多数不收敛且时间较长，现场应用不方便。针对这个问题，S.T.Lee 等［12］提出了解析的三线性流模型，计算速度虽然得到很大提升，但中后期的误差很大，因此本文提出适用于各个阶段的有限导流裂缝模型解析解。当存在邻井干扰时，业内通常在单井试井模型基础上运用叠加原理获得测试井的压力响应［13］。林加恩等［14］建立了适合于直井的油藏注采系统多井压力恢复干扰试井分析方法。李顺初等［15］、李成勇等［16］研究了均质无限大储层2 口直井共同生产时的干扰试井模型。程时清等［17］建立多级压裂水平井干扰试井模型，通过干扰试井判断来水方向。A.Uraiet 等［18］把裂缝考虑为均匀流量裂缝，利用干扰试井分析方法确定压裂裂缝的延伸方向和位置。H.Cinco−Ley 等［19］在Uraiet 等模型的基础上提出有限导流垂直裂缝干扰试井模型。目前考虑邻井干扰情况下的有限导流裂缝解析试井分析方法未被提出。

针对多井试井分析中半解析和数值解计算速度、收敛性和解释精度问题，本文提出多井干扰下有限导流裂缝井解析试井分析方法，不仅大幅降低试井反演时间，还能获取邻井干扰发生时间、干扰量、干扰井位置和地层参数，应用于长庆油田某区块，解释效率和精度显著提高。

1 邻井干扰下有限导流裂缝井解析试井模型

均质无限大储层中存在1 口压裂直井，该井作为测试井，周围n口直井作为干扰井以定产量生产（图1）。

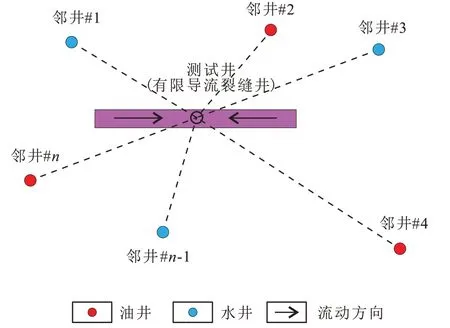
图1 垂直裂缝井邻井干扰示意（俯视）Fig.1 Sketch of adjacent well interference for vertical fractured well（Top view）

基本假设：①裂缝以井筒为中心对称，半长为xf，宽度为bf，高度为h（地层厚度），无因次导流系数为FcD；②邻井以产量qj（j=1，2，3，…，n）生产，不考虑井储和表皮效应；③地层孔隙度为φ，渗透率为K，原始地层压力为pi，综合压缩系数为Ct，流体黏度为μ；④地层流体只通过裂缝向井筒供液，基质向裂缝供液而不直接流入井筒；⑤单相微可压缩流体流动符合达西定律，忽略毛管力和重力影响；⑥井筒以定产量qw生产（井底产量），考虑井储和表皮效应。

模型的建立如图2 所示，有限导流和无限导流裂缝的井底压力（pwD）双对数曲线仅在早期流动阶段（线性流和双线性流）存在差异，在中后期两类裂缝的压力响应几乎一致。根据这个现象，利用三线性流模型和无限导流裂缝模型的早期近似解建立导流能力影响函数来表征两类裂缝早期压力响应的差异（标号①），然后叠加无限导流裂缝解（标号②）获得有限导流裂缝模型的解析解。在此基础上利用叠加原理得到邻井干扰下的有限导流裂缝模型的解析解。

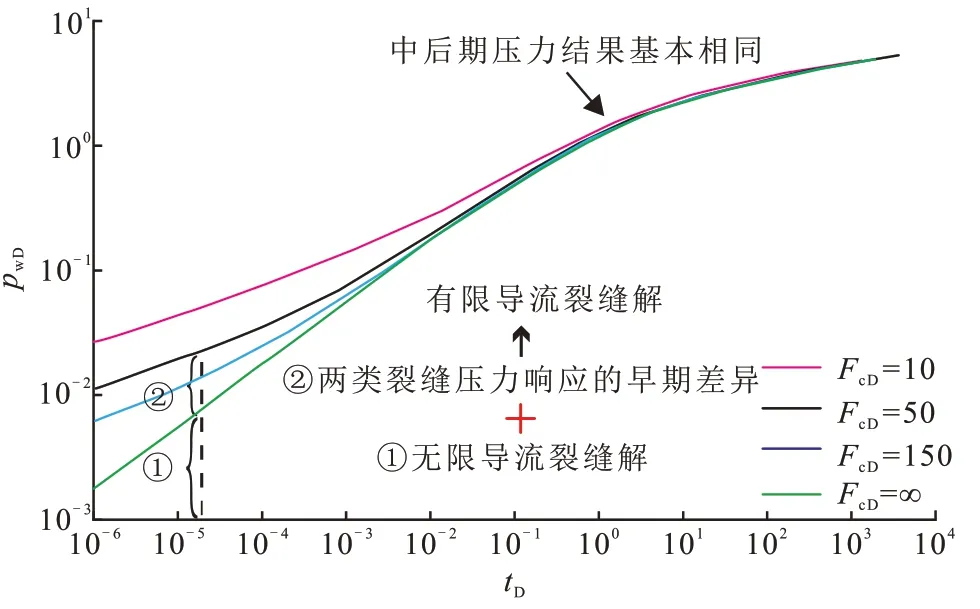
图2 有限导流和无限导流裂缝压力响应差异Fig.2 Pressure response difference between finite conductivity and infinite conductivity fractures

为方便模型建立，需要给出无因次定义，公式为：

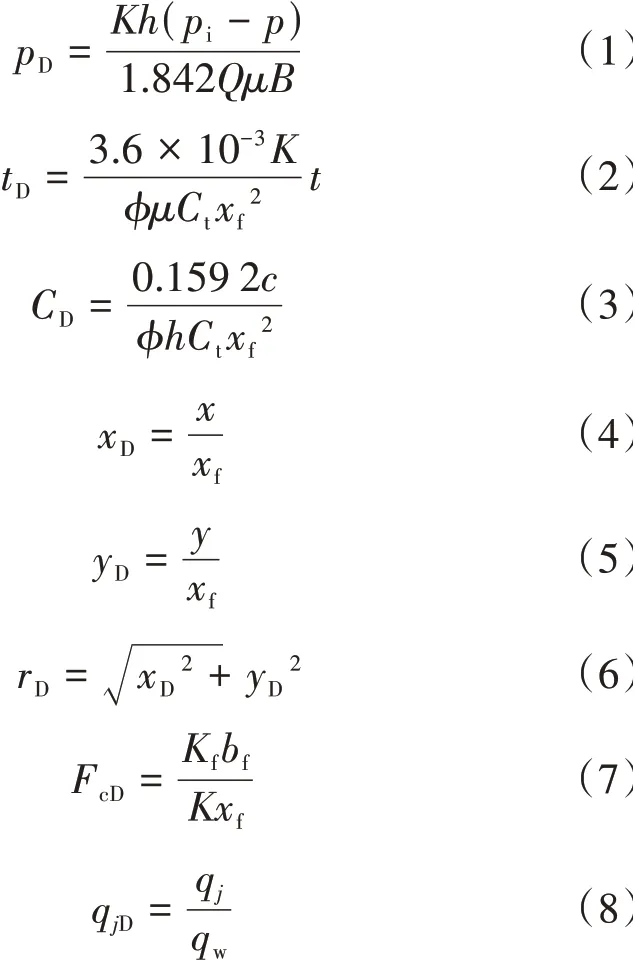
式中：p——地层压力，MPa；Q——油气井产量，m3/d；B——体积系数；t——时间，h；c——井筒储集系数，m3/MPa；x—横轴坐标距离，m；y——纵轴坐标距离，m；Kf——裂缝渗透率，10−3μm2；bf——裂缝宽度，m；pD——无因次压力；tD——无因次时间；CD——无因次井储系数；xD，yD，rD——无因次坐标系统；FcD——无因次裂缝导流系数；qjD——第j口邻井无因次产量。

首先，根据S.T.Lee 等［12］提出的三线性流模型，同时考虑到裂缝体积较小，裂缝内流动近似为一维稳态渗流，给出三线性流模型的解（详细步骤可查阅文献［12］，不再赘述），公式为

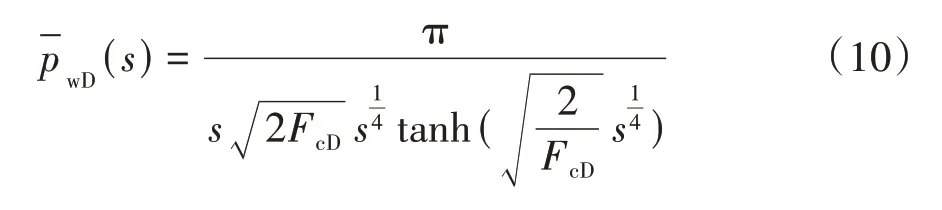
至于无限导流裂缝解，A.C.Gringarten 等［20］在均匀流量裂缝模型的基础上提出将计算点设置在裂缝长度的0.732 处获得井底压力解，公式为

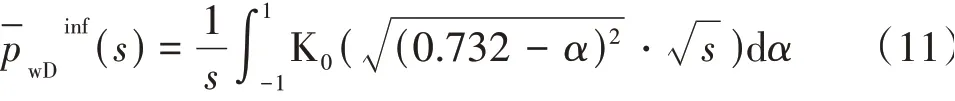
式中 K0——第二类0阶修正贝塞尔函数。

解析反演式（11），得

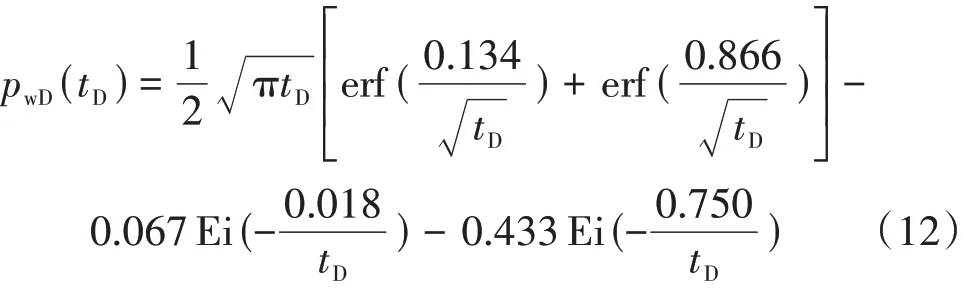
当时间处于早期时，误差函数趋近于1，指数积分函数趋近于0，式（12）简化为

对式（13）进行Laplace 变换得到无限导流裂缝模型在Laplace 空间的早期近似解

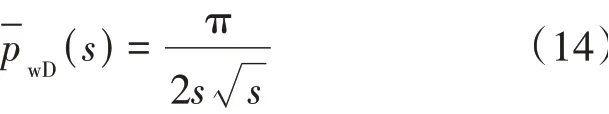
根据式（10）和式（14）初步得到导流能力影响函数的表达式为

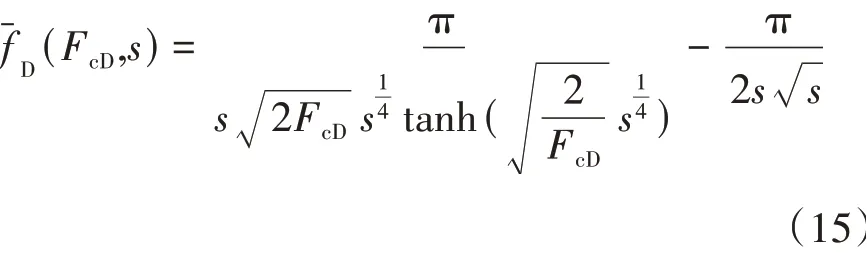
如图2 所示，无限导流裂缝解（式（11））和叠加导流能力影响函数（式（15））得到有限导流裂缝模型的解析解为

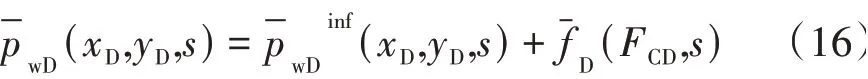
由于在线性流和径向流之间的过渡段，本文的解析解与Cinco−Ley 等提出的半解析解计算结果存在差异，本文参考A.F.Wilkinson［21］的工作并结合模型的无因次定义给出修正项，即

最终，根据式（16）和式（17）得到有限导流裂缝模型的解析解

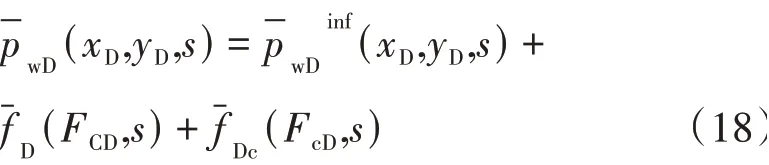
考虑井储和表皮效应，借鉴A.F.Van Everdingen 和W.Hurst［22］的工作得到井底压力解为

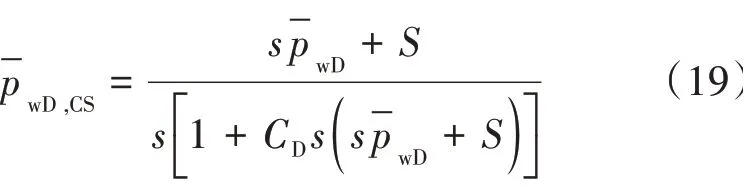
当存在邻井干扰的情况时，在单井模型的基础上运用叠加原理获得测试井的井底压力解。考虑邻井为定产量生产，首先得到其在测试井处的压力干扰为

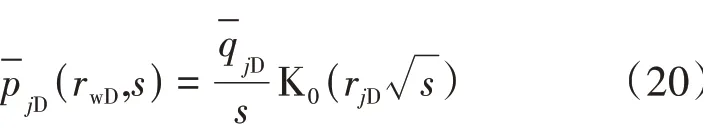
式中：rjD——第j口干扰井距测试井的无因次距离；pjD——第j口干扰井在测试井处产生的干扰压力；rwD——无因次径向距离。

在公式（19）的基础上运用叠加原理即获得多井干扰下有限导流裂缝井的解析解为

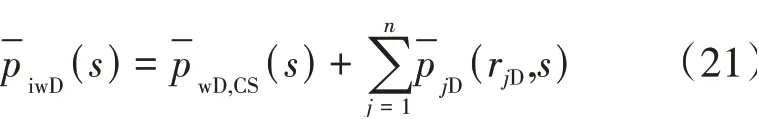
其中，piwD表示邻井干扰下有限导流裂缝的井底压力解，第1 项为考虑井储表皮效应的有限导流裂缝解析解，第2 项为邻井在测试井处产生的压力干扰。公式（21）同样可用于气井试井分析，此时压力变为规整化的拟压力，时间变为规整化的拟时间。

2 模型验证

利用Saphir 软件数值试井模块（Numerical Analysis）构建数值模型，用以验证提出模型的准确性，非结构PEBI 网格兼有笛卡尔网格的规则性和有限元网格的灵活性，方便处理裂缝附近的网格加密，因而使用非结构PEBI 网格离散整个油藏区域。如图3 所示，垂直裂缝井位于区域中心，设置地层渗透率为10×10−3μm2，孔隙度为0.2%，综合压缩系数为1 GPa−1，地层厚度为10 m，流体黏度为1.2 mPa·s，裂缝半长为100 m，测试井产量为10 m3/d，考虑4 口注水干扰井，单井注水量为1.5 m3/d，干扰井距测试井为300 m，数值模型中不考虑井储系数和表皮的影响。设置了6 组不同无因次裂缝导流系数（0.5，1，2，10，50，100）的模拟，用以对比本文模型和数值模型的结果。如图4所示，当无因次裂缝导流系数小于1 时（这种情况较少发生：因为低渗储层往往地层渗透率较低，而填砂裂缝的渗透率很高，FcD一般大于1），模型计算的中后期结果误差较大，大于1 时和数值模型的结果没有差异。

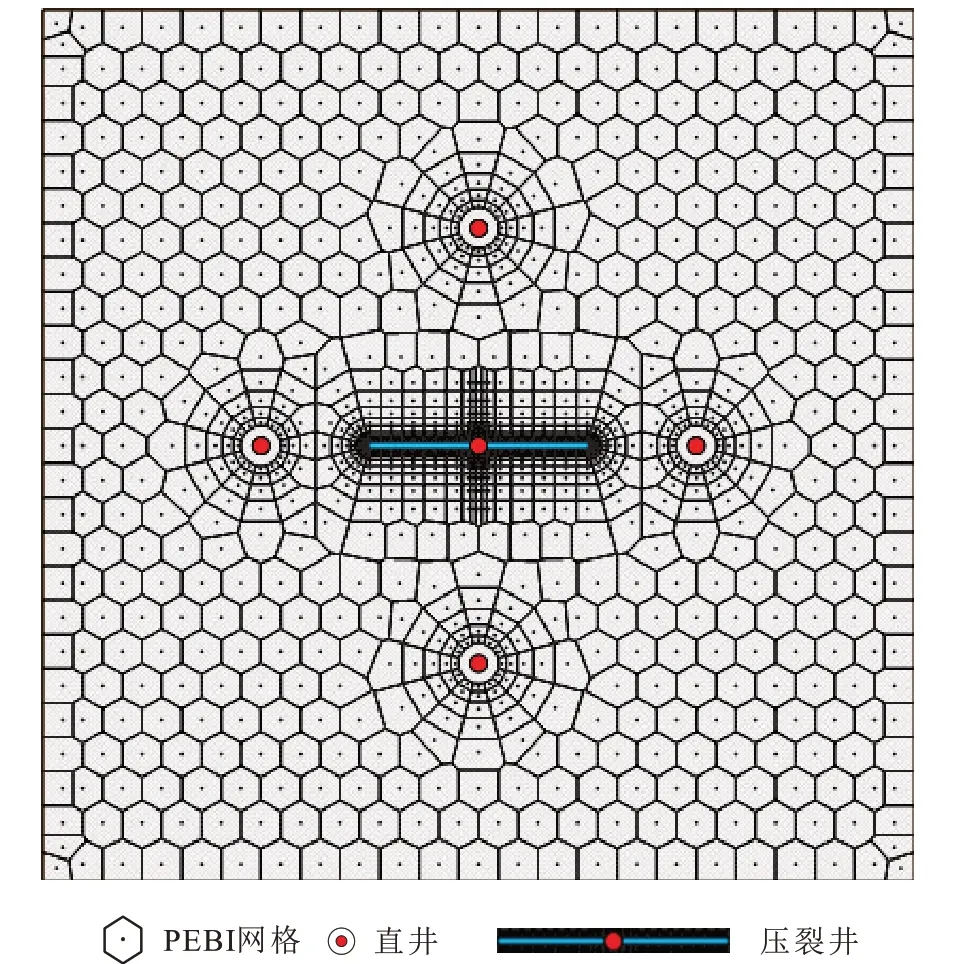
图3 数值模型离散示意（俯视）Fig.3 Sketch of numerical model discretization（Top view）

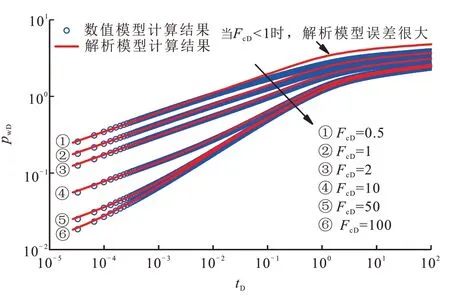
图4 解析模型和数值模型压力计算结果对比Fig.4 Comparisons of pressure calculation by analytical and numerical models

3 邻井同时生产压降曲线特征

由式（12）可知，邻井对测试井的干扰主要影响因素是邻井产量和井间距离，根据2 个因素的组合关系，讨论3 种情形。在敏感性分析中，设置1 口测试井和3 口干扰井，无因次井储系数为0.001，表皮系数为0.01，无因次裂缝导流系数为10π。

3.1 邻井产量不同、井距不同的情形

图5为均质储层中1口有限导流裂缝井（测试井）和3 口油井同时生产的压降曲线，3 口油井的无因次产量分别为1，3，5，情形（a）中，油井1、油井2、油井3 的无因次距离分别为2 000，200，20；情形（b）中，油井1、油井2、油井3 的无因次距离分别为20，200，2 000。两种情形的典型曲线皆存在4 个径向流段，两种情形对比可以看出，邻井与测试井的无因次距离越小，产生的影响越快；邻井的无因次产量影响4 个径向流段“台阶”的高度。

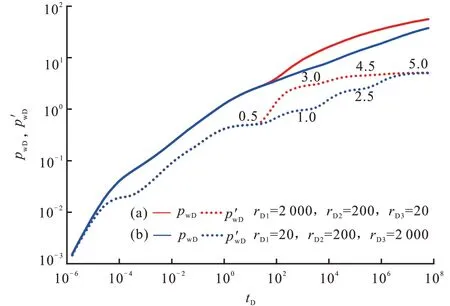
图5 邻井产量不同、井距不同情形下压降典型曲线Fig.5 Typical pressure drop curves with different production and different spacing adjacent wells

在情形（a）中，第1 径向流段（0.5 水平线）反映测试井本身的特征；根据邻井的位置分布，第2 径向流段反映干扰井3 的生产特征，其无因次产量为5，对应水平线的纵截距为3；第3 径向流段反映干扰井2，3 的生产特征，其无因次产量分别为3，5，对应水平线的纵截距为4.5；第4 径向流段反映干扰井1，2，3 的生产特征，其无因次产量分别为1，3，5，对应水平线的纵截距为5.0。因此，总结得到水平线纵轴截距是生产井无因次产量代数和的0.5 倍，即关于上述结论，后文将给出理论证明。对于情形（b）也有相同的结论。

3.2 邻井产量相同、井距不同的情形

邻井与测试井的无因次井距主要影响干扰时间的早晚（图6），第1 径向流段为测试井自身的生产特征反映，第2、3、4 径向流段按照无因次井距大小分别是邻井1，1 和2，1 和2 和3 的生产特征反映，而水平线的纵轴截距则是测试井和对测试井产生影响的邻井无因次产量代数和的1/2。

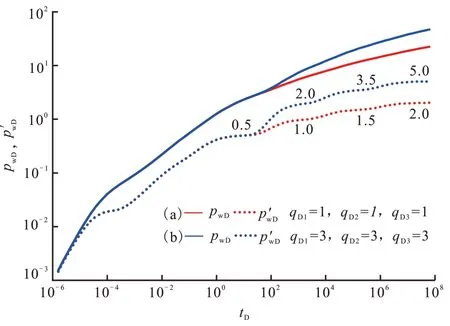
图6 邻井产量相同、井距不同情形下压降典型曲线Fig.6 Typical pressure drop curves with equal production and different spacing adjacent wells

3.3 邻井井距大致相等的情形

当邻井与测试井的无因次井距近似时，在压降典型特征曲线（图7）上将只有2 个径向流段，第1个径向流段（0.5 水平线）是测试井自身的生产特征反映，而第二个是所有井生产特征反映的总和。由于无因次井距近似，所有邻井干扰基本同时反映，此时不会出现前面的“多台阶”曲线特征。

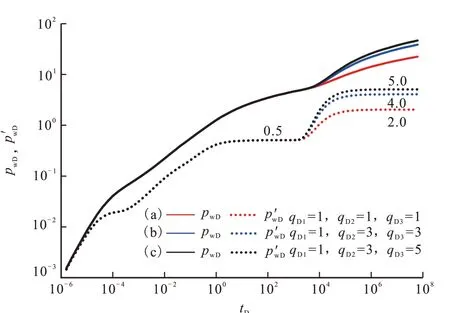
图7 邻井井距大致相同的情形下压降典型曲线Fig.7 Typical pressure drop curves with roughly equal spacing adjacent wells

3.4 邻井干扰下压力导数曲线特征理论

从式（21）可以看出，邻井干扰下有限导流裂缝解析解由3 项组成：无限导流裂缝解析解项、导流能力影响函数项和邻井干扰项。在时间处于后期时，导流能力影响函数的值稳定于一个定值（图8），其压力导数的值为0。因此，邻井干扰下有限导流裂缝压力导数晚期近似解仅需考虑无限导流裂缝解析解项和邻井干扰项。

（1） 式（12） 是 无 限 导 流 裂 缝 模 型 经 过Laplace 解析反演后的实空间表达式，当tD＞2 时，式（12）简化为

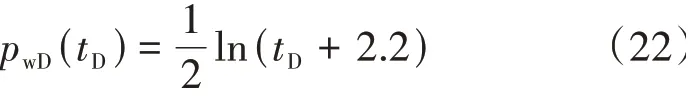
（2） 对于邻井干扰项，以一口井为例进行Laplace 解析反演，公式为

根据指数积分函数的性质，式（16）可写作

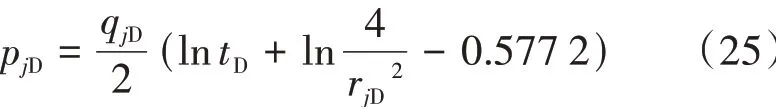
将式（23），式（25）代入式（21）得到晚期近似解

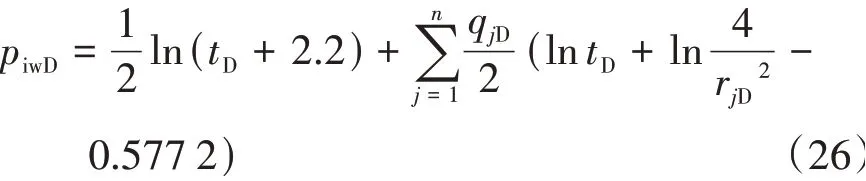
在式（18）中，对时间对数求导可得

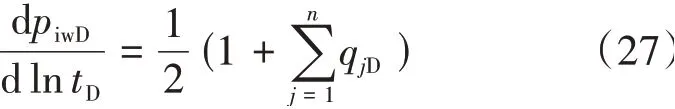
由式（19）可知，压力导数曲线径向流段纵截距是测试井和产生影响的邻井无因次产量代数和的1/2。

4 应用实例

4.1 实例一

将本方法应用于长庆油田Z36 区块，其中Z16井油层中深为1 895.6 m，储层有效厚度为11 m，孔隙度为12.66 %，综合压缩系数为1.496 GPa−1，原油黏度为1.32 mPa·s，体积系数为1.26。Z16 井经过井下关井压恢测试657 h，其中有效测试时间388 h，实测压力为5.96~8.60 MPa，压力恢复速度较为缓慢。

Z16 井附近有1 口油井Z15（平均产液量为0.89 m3/d），2 口注水井Z17 和Z18（图9）。Z16 井含水率长期保持在10 % 左右， 产液量低（1.15 m3/d），注水不见效，排除注水井干扰的情况。根据压力恢复测试资料绘制双对数曲线（图10），压力导数曲线后期“下掉”并最终出现径向流，初步考虑存在附近油井Z15 井的干扰。采用模型解释，获得井储系数0.07 m3/MPa，表皮系数0.09，渗透率0.115×10−3μm2，裂缝半长23.91 m，裂缝导流系数136.43×10−3μm2·m，邻井干扰量为0.87 m3/d，与Z15 井的日产液量相近，初步证明Z16 井所受干扰来自Z15 井。另外，根据两口井的产量大小结合前文得到的认识可以判断测试井Z16井自身的径向流段水平线纵轴截距大概在0.5。因此，Z16 井尚未出现径向流段，油井Z15 的干扰信号就已到达测试井，干扰发生在压力导数刚出现下掉的时刻（第30 h）。

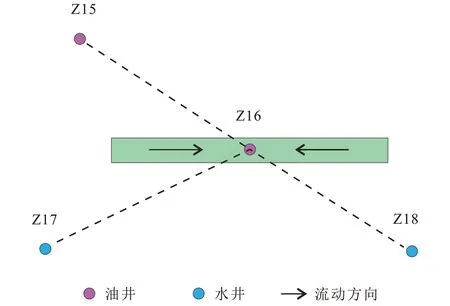
图9 长庆油田Z36区块井位示意（俯视）Fig.9 Sketch of well locations in Block Z36 of Changqing Oilfield（Top view）

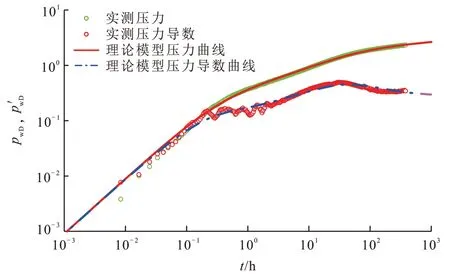
图10 长庆油田Z36区块Z16井双对数拟合曲线Fig.10 Log-log fitting of Well Z16 in Block Z36 of Changqing Oilfield

4.2 实例二

将本方法应用于长庆油田B157 区块，其中G30 −48 井是一口未压裂的注水井，日注水量10 m3，关井压降测试480.4 h，油层中深为1 978 m，储层有效厚度为19.7 m，孔隙度为11.19 %，综合压缩系数为1.5 GPa−1，原油黏度为1 mPa·s，体积系数为1。如图11 所示，G30−48 井压力双对数曲线出现线性流特征，判断该井附近形成了诱导裂缝。压力导数曲线在后期“下掉”并出现径向流，同时结合周边井的产液量情况及井的位置分布，判断注水井间形成了水窜通道，该井在测压过程中受到了邻井干扰。采用本文模型解释G30−48 井的压力测试资料，获得井储系数0.48 m3/MPa， 表 皮 系 数0.001， 渗 透 率1.08×10−3μm2，裂缝半长22.01 m，裂缝导流系数21.04×10−3μm2·m，邻井干扰量为6 m3/d，结合各井累计产液量情况，进一步明确了水窜通道和干扰来源。

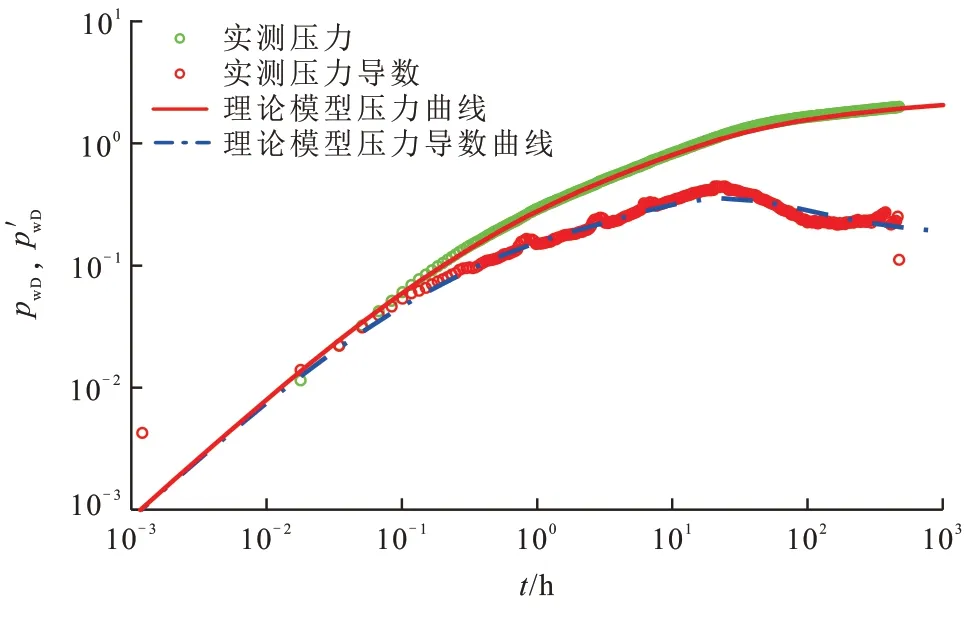
图11 长庆油田B157区块G30-48井双对数拟合曲线Fig.11 Log-log fitting of Well G30-48 in Block B157 of Changqing Oilfield

5 结 论

（1）提出多井干扰下有限导流裂缝解析试井模型，相较于前人的半解析解和数值解，该方法的优势在于大幅提高了计算速度，缩短了拟合时间。

（2）模型晚期近似解及理论曲线表明：径向流段水平线的纵截距实际是测试井和产生影响的邻井无因次产量代数和的1/2。

（3）邻井干扰下垂直裂缝井试井典型曲线会出现“多台阶”特征，反映了自身和邻井的生产特征，根据“台阶”的数量和高度可判断干扰井的数量及干扰发生的顺序。

（4）实例分析表明通过实测曲线径向流段的高程差结合测试井和干扰井的产量可判断邻井干扰发生时间、干扰量和地层参数，结合地质和生产动态资料，可进一步确定干扰井的位置和分析水窜通道。