非均质致密油藏压裂水平井产能预测模型
马亮亮
(中国石油大庆油田有限责任公司开发事业部,黑龙江 大庆 163002)
0 引 言
近年来,以致密油等为代表的非常规资源已成为国内外油气上产的主力。该类油藏孔喉结构复杂、储层物性差、流动阻力大,压裂水平井作为提高油井产量和单井控制储量的有效方式之一,在其开发中得到广泛应用[1-7]。由于致密油储层非均质性、复杂地应力、天然裂缝、人工裂缝等影响,压裂水平的产能预测变得十分复杂,国内外许多学者进行了研究[8-14]。另外,B.Y.Guo 等[15]利用杜哈美原理推导出了垂直缝导流能力有限时的裂缝与油藏流体耦合方程,同时使用拉普拉斯变换和边界元方法求解方程;魏漪等[16]依据叠加原理和椭圆渗流理论,推导出水平井在压裂后垂直裂缝相互干扰情况下的非稳态产能计算方程。已有模型在渗流特征、裂缝参数及缝间干扰方面考虑比较全面,但很少考虑长水平井条件下致密储层的非均质性问题,对于长水平段水平井产能预测有一定的局限性。
本文在建立模型时考虑水平井穿过区域储层物性的非均质性,同时考虑了天然裂缝与人工裂缝之间的耦合问题,基于矩形区域拉普拉斯空间Green函数基本解,离散人工裂缝和储层不同渗透率分区边界,建立了非均质致密油藏水平井单井模型,对非均质致密油藏长水平井的开发具有指导意义。
1 压裂水平井渗透率分区数学模型
1.1 模型假设
模型将沿水平井井筒方向的储层分为多段不同渗透率的非均质储层,储层外边界封闭,相邻渗透率分区在分区界面处压力和流量连续。为了便于描述非均质储层内的流体流动规律,提出5 点假设:(1)储层分区单元内为均质、各向同性储层;(2)裂缝在纵向上压穿整个储层;(3)流体流动为二维单相微可压缩非稳态渗流;(4)忽略重力的作用;(5)裂缝的导流能力不随时间改变。
1.2 流体在油层中的渗流模型
对于单相流体在四周封闭的水平、各向同性储层中流动,将渗流方程[17]进行拉普拉斯变换,其表达式为
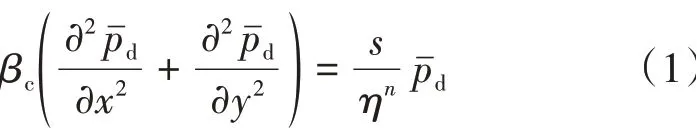
其中:
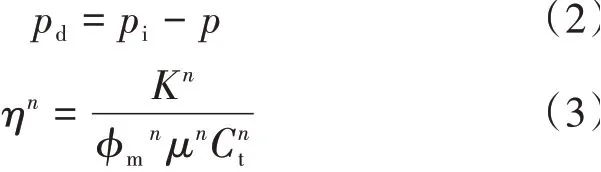
式中:βc——单位换算系数,取0.086 4;pd——地层中某点压降,MPa;pˉd——pd在拉氏空间的值,MPa;s——拉普拉斯变量;n——油层数;ηn——各渗透率分区导压系数,10−6m2/s;pi——地层原始压力,MPa;p——地层任意点压力,MPa;Kn——各分区渗透率,10−3μm2;φmn——各分区基质孔隙度;μ——各区原油黏度,mPa ⋅s;Ctn——流体岩石总压缩系数,MPa−1;NK——渗透率分区数;n——不同分区,n= 1,2,…,NK。
式(1)加上初始条件pˉd= 0 与内外边界条件,构成了油藏内部完整的渗流数学模型,将裂缝网格和边界网格处理为四周封闭条件下拉普拉斯空间的点源函数积分解,各渗透率分区中任意一点格林函数基本解[18]为
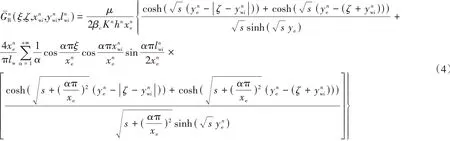

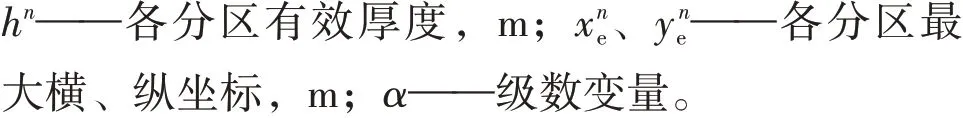
将裂缝和分区边界进行网格离散,建立基质渗流边界积分方程公式为
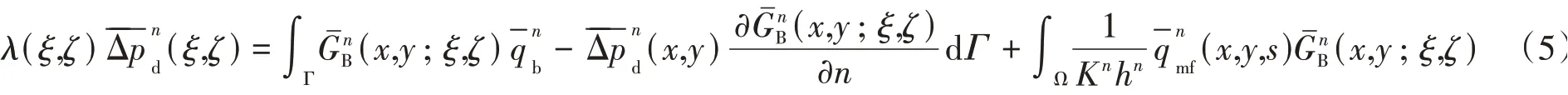
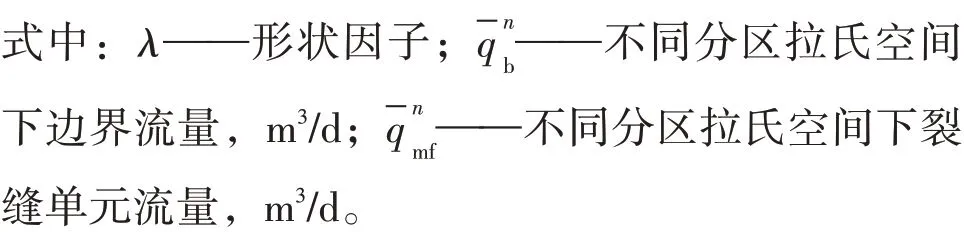
因为四周边界封闭为
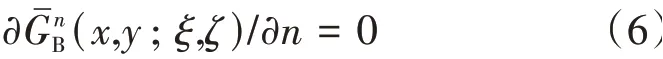
由式(6)写成的离散形式为
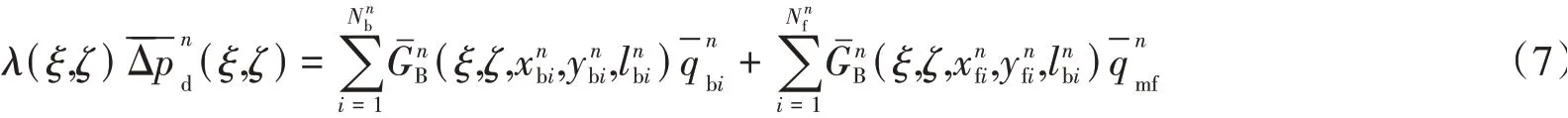

分区分界面处压力相等,流量相反,即
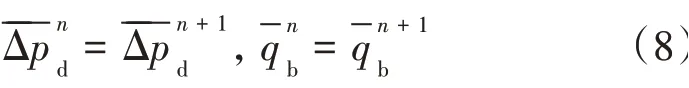
所以,分界面处离散边界元的公式为
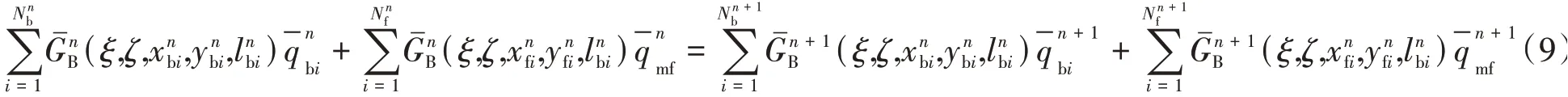
1.3 裂缝内流动模型
人工压裂裂缝具有孔隙度小、导流能力强的特点,流体在裂缝中的流动可简化为稳定线性流动[19],裂缝内部拉氏稳定渗流方程为
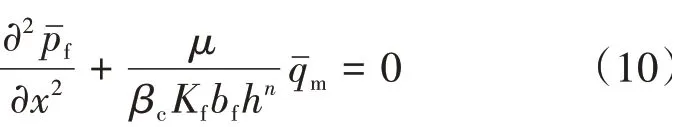
式中:pf——裂缝内压力,MPa;pˉf——pf在拉氏空间 的 值,MPa;Kf——裂 缝 渗 透 率,10−3μm2;bf——裂缝宽度,m;qm——基质向裂缝中的窜流量,m3/d;qˉm——qm在拉氏空间的值,m3/d。
此时外边界条件为裂缝趾端封闭不流动,内边界为定井底流压。将单条裂缝离散为2×m个等间距的网格,根据对称性,裂缝左翼任意相邻网格中心的压力差表达式为
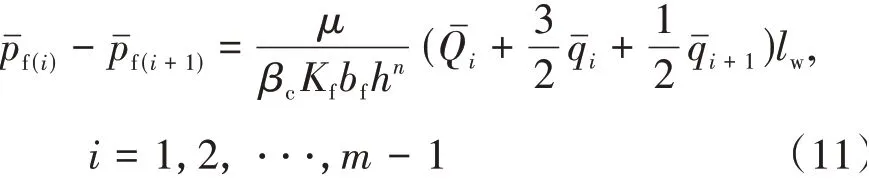
其中

式中:Qi——裂缝内流入裂缝单元i的流量,m3/d;Qi——Qˉi在拉氏空间的值,m3/d;qi——裂缝i单元内的流量,m3/d;qi+1——裂缝i+1 单元内的流量,m3/d;lw——井筒网格长度,m。
井筒所在网格与井底流压的关系表达式为
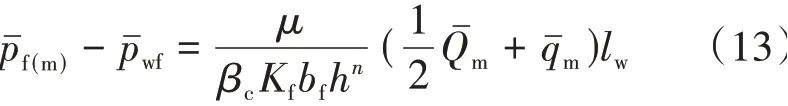

1.4 模型耦合及求解
对于基质向裂缝的渗流,以及不同渗透率分区之间的流体交换可以联立式(7)和式(10)得到矩阵的形式,即
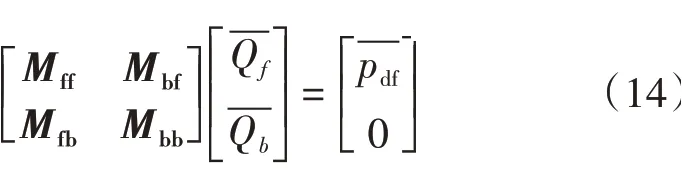

对于裂缝内的流动,基于式(11)和式(12)建立裂缝单元的流动方程,因为人工裂缝缝面处的油藏压力和人工裂缝压力相等,所以单条裂缝左翼单元的压力与井底流压的关系为
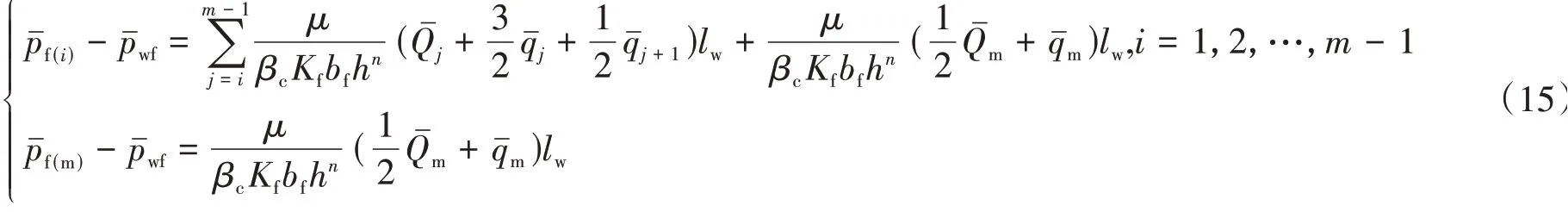
其矩阵形式为
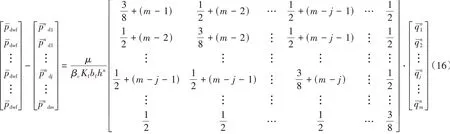
根据对称性,单条裂缝右翼单元表达式和矩阵形式与式(17)相同。令
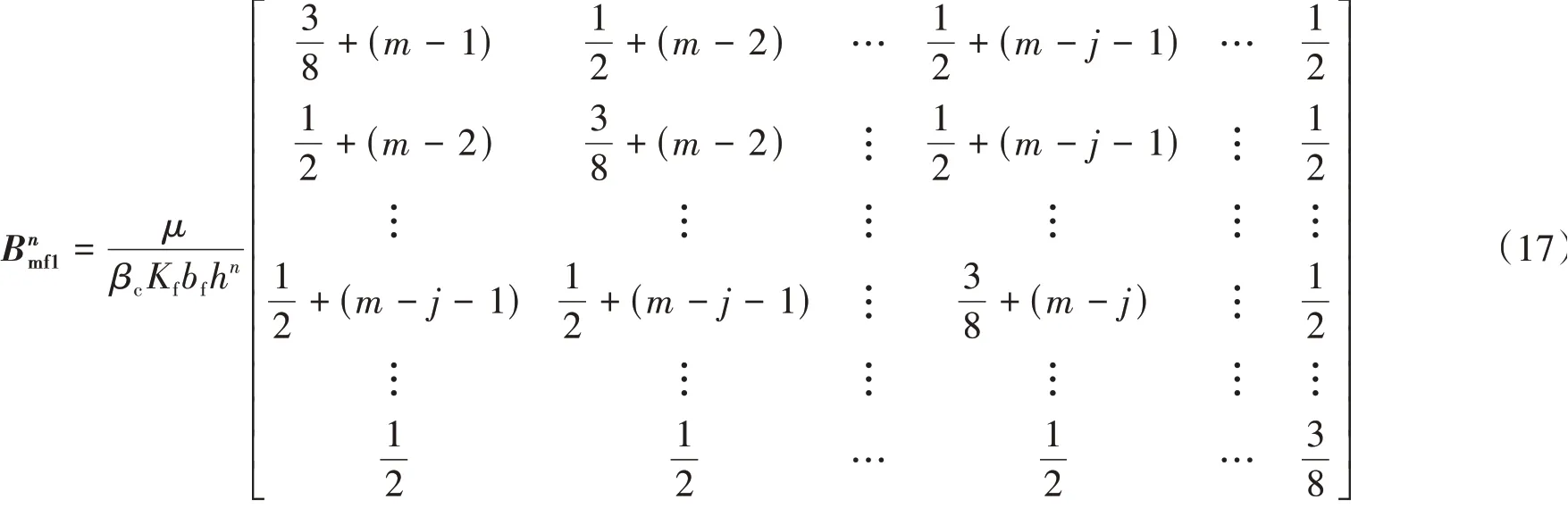
根据对称性,单条裂缝右翼单元矩阵元素为
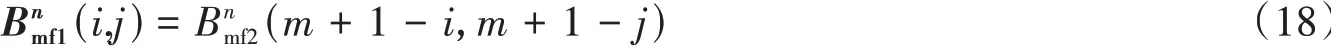
全区裂缝总的流动附加矩阵为
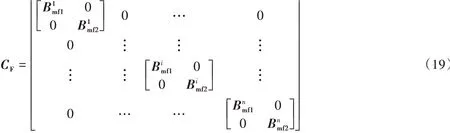
裂缝流动的表达式为
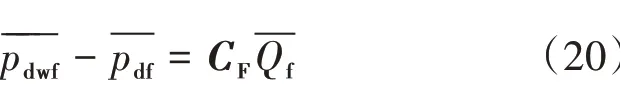
根据式(14)建立的裂缝单元流动方程为
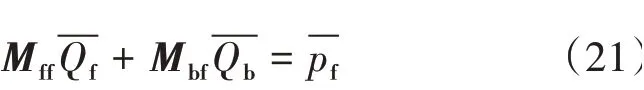
由式(14)、式(20)、式(21)建立了不同渗透率分区内基质向裂缝流动以及裂缝内流动的耦合数学模型
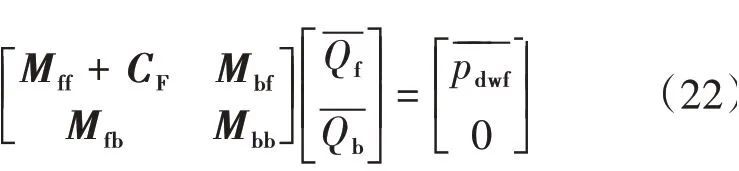
求解矩阵,得到拉氏空间下裂缝内总流量,最后,通过拉普拉斯数值反演求得致密油藏压裂水平井考虑沿程非均质性条件下的产量。
2 模型应用
2.1 流动阶段及流动形态
油井开井生产后,储层向裂缝流动,压力逐渐向外传播。图1 为应用模型计算得到不同流动阶段储层压力的分布情况及对应的流场。
早期裂缝线性流阶段(图1(a)):压裂水平井刚开井生产时,裂缝附近流体流向裂缝,以垂直于裂缝平面的线性流动为主,储层动用面积小。中期拟径向流阶段(图1(b)):随着时间的增加,压力向外传播,裂缝附近形成低压区,远处流体拟径向流入裂缝低压区。后期拟稳定流动阶段(图1(c)):当压力波传播到储层边界后,整个储层为拟稳定流动。图1(d)为不同生产时间流体在地层中流动阶段的划分。
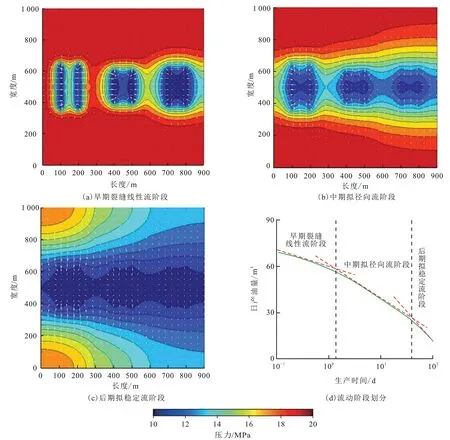
图1 不同流动阶段的储层压力场及流线分布Fig.1 Reservoir pressure field and streamline distribution in different flow stages
2.2 渗透率级差对产量的影响
为研究压裂水平井沿程非均质性对油井产量的影响,分别对相同平均渗透率,不同渗透率级差情况下(ε=5,10,20,40)油井产量的差异进行研究。模型参数如表1 所示。图2 为不同渗透率级差下油井的生产曲线。由图2 可以看出,渗透率级差主要对油井生产的早期有较大影响,油井产量随渗透率级差的增加而减小,随生产的进行,由于模型边界为封闭边界,储层平均压力下降较快,渗透率级差对产量的影响不再明显。通过以上分析,压裂水平井的沿程非均质性对油井生产有一定影响,在实际生产过程中,非均质作用不可忽略。
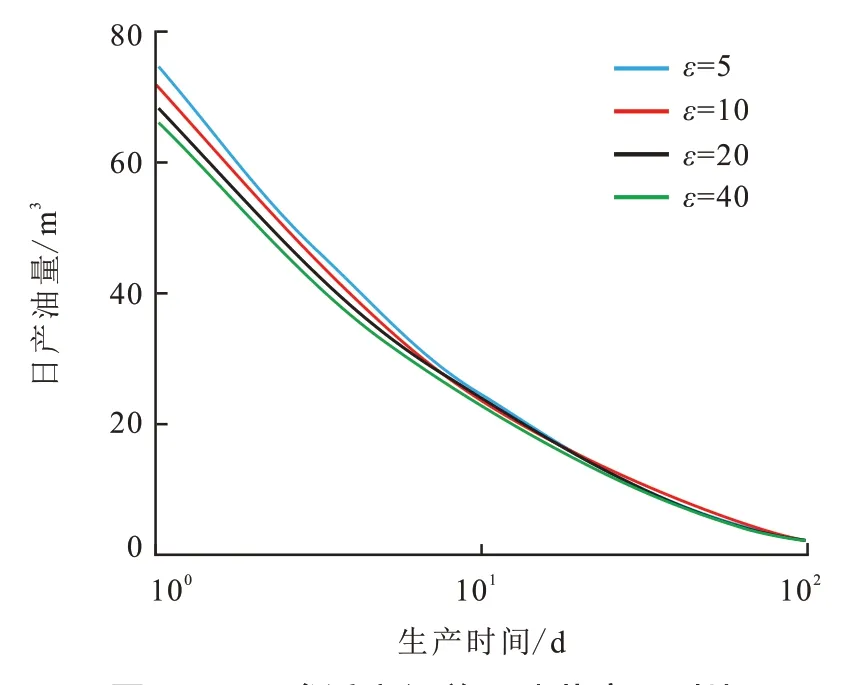
图2 不同渗透率级差下油井产量对比Fig.2 Comparison of oil well production with different permeability contrast
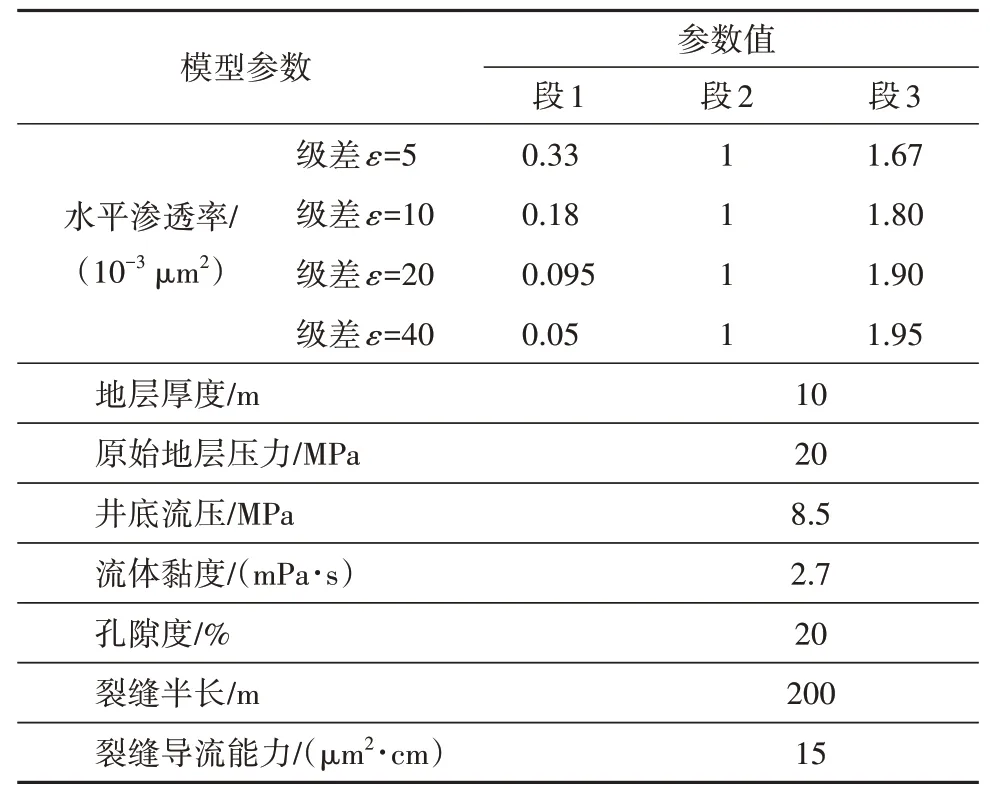
表1 不同渗透率级差模型参数Table 1 Parameters of different permeability contrast models
2.3 应用实例
以大庆长垣外围某致密油田为例进行现场试验。致密油层平均孔隙度为12.2%,基质平均渗透率为0.52×10−3μm2,喉道半径主要为0.1~1.0 μm,平均为0.4 μm,为低孔细喉致密储层。井区天然裂缝发育,密度为5 条/m,天然裂缝与井筒夹角约35°, 油 层 厚 度 为3.3 m, 原 始 地 层 压 力 为18.5 MPa,井底流压为8.5 MPa,原油密度为0.83 g/cm3,原油体积系数为1.052,原油黏度为1.43 mPa·s,有效水平井长度为1 500 m,人工压裂裂缝为16 段,每段2—3 簇,平均裂缝半长200 m,裂缝与井筒角度平均为57°(图3)。
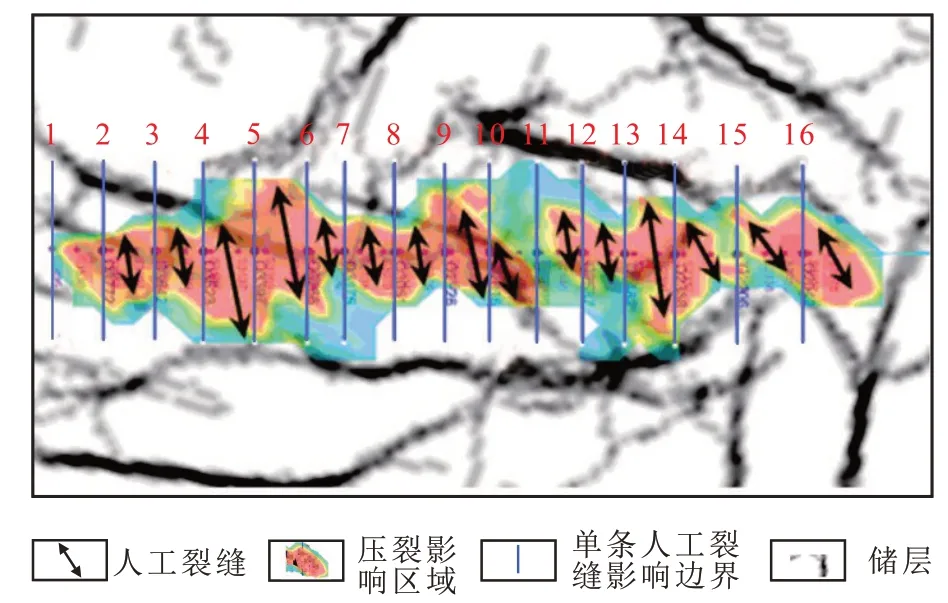
图3 压裂水平井微地震监测Fig.3 Micro-seismic monitoring of hydraulic fractured horizontal well
根据所建立的非均质致密油藏压裂水平井产能预测模型,计算不同时间的油井日产油量,并与实测生产曲线进行对比(图4),模型计算结果与实际生产日产油量最大误差为6.7%,计算结果与实际值基本吻合。该模型可用于非均质致密油藏水平井的产量预测。
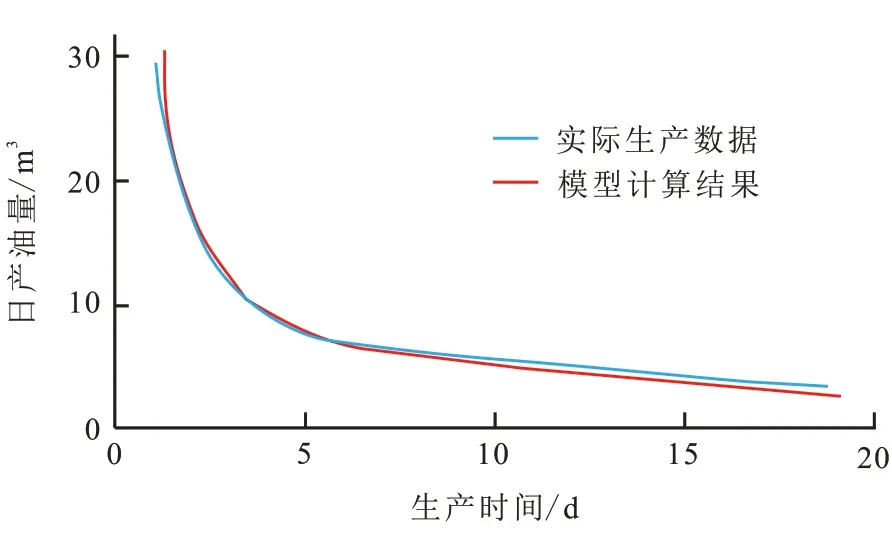
图4 模型结果与实际生产曲线对比Fig.4 Comparison between simulation and actual production
3 结 论
(1)基于拉氏空间下Green 函数的基本解,通过将裂缝及渗透率分区边界进行离散,推导得到非均质地层压裂水平井渗流边界元方程,并通过Stehfest 数值反演,得到了压裂水平井定井底流压条件下的产能,可很好地指导非均质致密油藏长水平井开发。
(2)边界元基本解采用了通过叠加原理推导得到矩形封闭边界条件下的格林函数,其优点为在分区边界上导数为零,减小了边界耦合的变量个数,提高了计算效率。
(3)通过求解模型得到产量曲线,根据产量双对数曲线特征将储层流体流动划分为3 个阶段:早期裂缝线性流阶段、中期拟径向流阶段、后期拟稳定流阶段。
(4)对于非均质储层,非均质性对水平井产量的影响不可忽略。相同平均渗透率,渗透率级差越大,产量越小,但随着生产进行,渗透率级差对产量的影响逐渐减小。

