全国青少年Python等级考试试题测评研究

乔 璐

(扬州大学，江苏 扬州 225000)

0 引言

已有的系统地评价学生编程能力的方法并不多，有关编程能力的评价往往在科学性和实践性上都不尽人意，阻碍了学生编程能力的提高。一方面，已有的有关编程能力的评价方法缺乏明确的评价标准，教师们在面临庞大的知识点时，关于具体知识点对应哪些计算思维要素，以及这些要素之间的关系缺少清晰的认识；另一方面，现有的Python 等级考试评分方式关注的都是学生回答问题的结果是否与制定的标准答案一致，而没有体现学生在编程过程中思维结构的复杂程度，应当先确定评判编程能力层次的关键要素是什么以及这些要素是通过怎样的外显行为来体现。因此本研究致力于Python 试题分析方法的构建，包括评价要素的提取、试题所处的思维水平层次的划分以及Python 等级考试两种题型的应用范例来确立试题评价标准。

1 文献回顾

1.1 SOLO评价的应用

1.1.1 SOLO的基本含义

SOLO 是一种以等级描述为特征的质性学业评价方法，也称为“可观察的学习成果结构”。比格斯（Biggs）把学生对具体问题可观察的学习结果划分成5种思维水平层次。

⑴前结构水平（Prestructural）：处于该水平的学习者思维混乱，未掌握知识点，回答与问题无关。

⑵单点结构水平（Unistructural）：只能运用一个知识点解决问题，并立刻得到结果。

⑶多点结构水平（Multistructural）：可以综合多个知识点解决问题，但知识点与知识点之间没有联系。

⑷ 关联结构水平（Relational）：可以综合多个知识点，且能将多个知识点联系解决问题，得出答案，知识网络初步形成。

⑸拓展抽象结构水平(Extended Abstract)：处于该水平的学习者不仅能够掌握问题情境中给出的多个知识点，将多个知识点联系，形成知识图谱解决问题，学习者的头脑中可以构建清晰的知识网络，而且回答的结果高度概括，抽象程度高，能够将结论应用到其他情境中。

1.1.2 SOLO分类理论应用于试题测评的现状分析

笔者通过在知网搜索SOLO 分类理论、应用两个关键词进行文献筛选与整理，从2010 年至今，发表有关SOLO 评价的试题应用为61 篇。2010年，张洪岩将SOLO 分类理论应用于高中英语的总结性评价中，提出了学业检测与分析的方案并在广州某高中进行了实施和结果分析。2011年，黄玉慧将SOLO 分类理论应用到高考语文卷的评价中，弥补了客观题评价标准“唯一”的问题。2012年，薛春兰将SOLO 分类理论应用到高一化学教学中，并指导高一化学教学的分层次教学。2013年，黄爱民对有关中学化学的SOLO分类理论的应用进行文献梳理工作，并为SOLO分类理论进一步的应用指明了方向。2014年，陶兴赋将其运用到江苏省扬州中考化学选择题的命制中，并给出了应用SOLO命制化学选择题的反思与不足。2016年，胡文秀将SOLO 分类理论应用到思想品德主观题的命制中，并给出了其实践效果。2017年，周小奋基于SOLO 分类理论对初中物理开放性试题命题及进行SOLO 分类评价方案实例分析。2018年，周光明基于该理论评价学生在地理学科外显的思维水平层次。2019年，郑艺芳、李雪峰基于SOLO 分类理论对2019年高考生物学试题进行分析，并对试题结构的合理性进行评价。由此可见，SOLO 分类广泛应用于英语、语文、化学、思政、地理、生物学科的教学设计与试题的分析命制中，但应用于信息技术的相关文献较少。

2 研究方法与研究过程

首先采用文献研究法将SOLO 评价的应用邻域以及计算思维评价的相关内容进行梳理。再采用案例分析法，在整理Python 等级考试试题所考察知识点的基础上，确立相应知识点对应哪些计算思维要素。最后再根据试题中涉及到的计算思维评价要素以及学生答题时可能出现的情况进行归纳整合，进而判断并整理试题考察的学生思维水平层次和编程能力。

2.1 全国青少年Python等级考试试题评价体系构建

我们给出评价要素与知识点的映射关系（表1）。针对试题考查的特性，仅选取计算思维三维框架中的计算概念作为评价要素，并将中国电子学会列出的全国青少年Python 等级考试一到四级所考查的知识点与对应的计算概念进行映射。

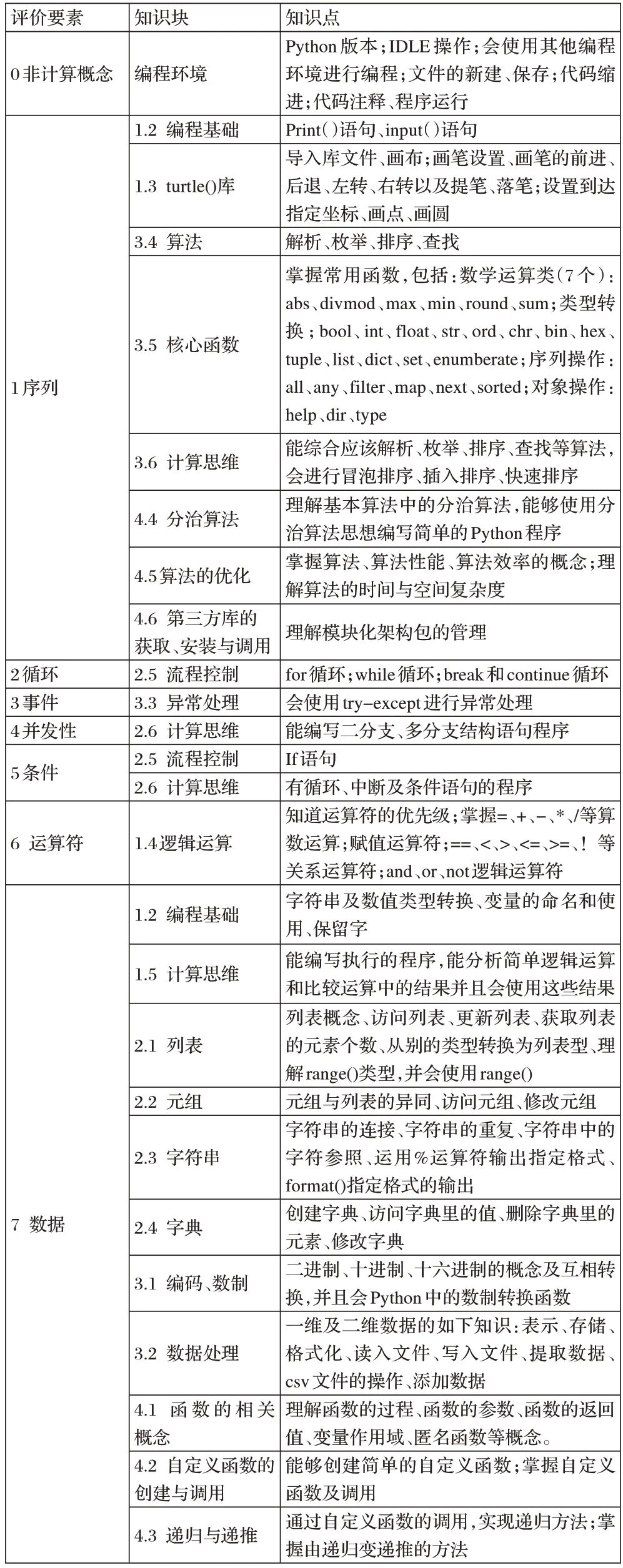
表1 评价要素与知识点的映射关系

2.2 试题分析方法的应用案例

笔者仅选取2020 年12 月份三级Python 等级考试试题，对不同难度的单选题和判断题进行纵向比较。下面是笔者将SOLO 分类理论思想运用于不同类型试题的测评中，从中我们可以了解不同难度试题所体现的思维层次和外显行为特征。由于前结构水平表现为“一问三不知”，对其进行评价时得到的答案大多是学生猜测、语意重复或随意作答。因此，排除前结构水平，对剩下四个水平结构进行研究。

2.2.1 单选题应用范例

在一份试题中，单选题共有25题，占全篇分值的50%。在分析单选题的过程中，首先明确题干和四个选项中考查的知识点，再将知识点映射到相应的计算思维评价要素上，最终根据学生解答该题目需具备的计算思维要素来确定该题所属的思维水平结构层次，如表2所示。

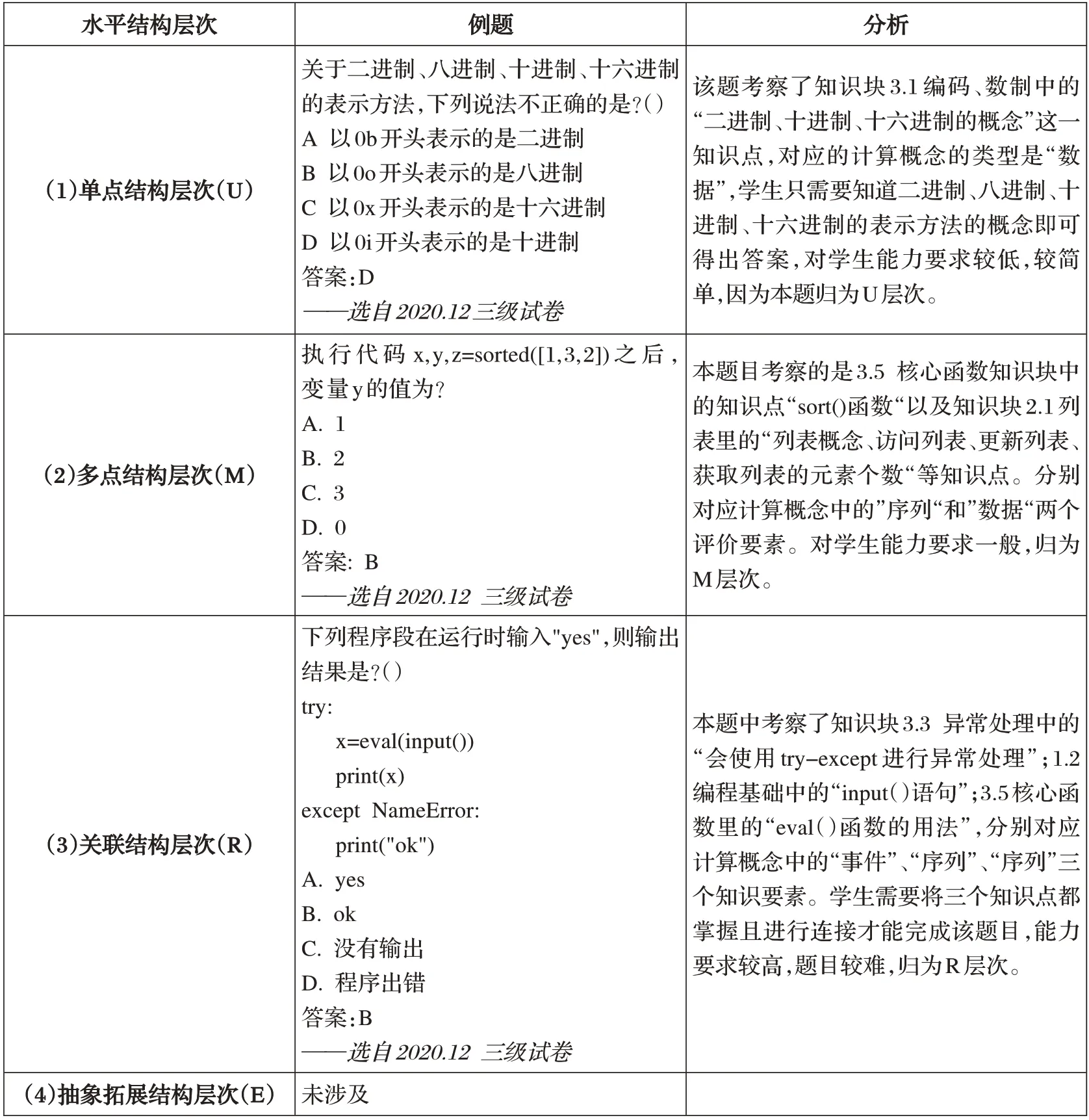
表2 单选题应用范例

2.2.2 判断题应用范例

判断题共考察十题，分值占试卷的20%。在分析判断题的过程中，首先明确题干中考查的知识点，再映射到相应的计算思维评价要素上，最后确定该题所在的思维水平结构层次，如表3所示。

表3 判断题应用范例

3 研究发现

在等级考试中，涉及“序列”和“数据”这两个评价要素的知识点较多，由此可见，计算思维中的“序列”和“数据”是评判编程能力的重要依据。不同题型所对应的SOLO 水平层次的比例有所侧重，对于单选题考察的SOLO 层次，侧重考察多点和关联结构水平，判断题则侧重考察单点和多点结构层次。

4 结束语

⑴由于Python 等级考试涵盖的知识点所对应的计算概念有所不同，老师可以依据学生对不同知识点的掌握情况进行统计分析，明确学生所缺乏的具体的计算思维内容，从而帮助教师有针对性的进行计算思维的培养与教学工作。

⑵依据SOLO分类理论，将Python等级考试的试题进行合理的层次划分，有助于试题的开发者建构更加清晰的试卷等级结构，开发者可以按照不同的等级，对各个等级试题所考察的思维水平有所侧重。

⑶本研究可以为全国青少年Python 等级考试的评分系统建立合适的模型，制定者可以依据试题所体现的思维水平层次来划分试题难度，从学生的角度出发，指导试题制定妥善的评分标准。