减振孔参数降振作用的灰色关联度分析
段宝福 张正欣 张春武 孙宗军
(1.山东科技大学土木工程与建筑学院,山东 青岛 266590;2.江汉大学爆破工程湖北省重点实验室,湖北 武汉 430056;3.中铁武汉勘察设计研究院有限公司,湖北 武汉 430074;4.青岛瑞翰科技集团,山东 青岛 266061)
近年来,不少学者对爆破降振进行了深入研究,一方面对爆破参数合理取值进行了研究,如汪平[1]设计了3种直眼掏槽爆破方案,以地下矿山斜坡道掘进为试验现场,通过对比试验发现,三空孔直眼掏槽爆破更有助于提高爆破掘进效率,并据此设计了爆破振动控制措施;林飞[2]通过改变数码电子雷管的微差时间来进行控制爆破对比试验,试验结果结合萨道夫斯基公式建立了振动速度的回归预测模型;范军平等[3]通过模型试验和数值模拟分析了大直径空孔直眼掏槽的爆破效果,得出大直径空孔的爆破振动速度和工作面破坏范围以及炸药能量消耗均小于小直径空孔掏槽,并且大直径空孔掏槽爆破深度提高了近20%;周传波等[4]研究了4种常见的直眼掏槽方式,运用LS-DYNA数值模拟软件定量计算了掏槽孔贯穿、节点运动速度等相关参数,得出单螺旋掏槽方式最优。另一方面研究了合理的振动爆破规律,如GAO等[5]根据应力波的传播特性,分析了断层地层中地震波的传播和衰减规律;张西良等[6]以某露天铁矿为例,测试了边坡上不同高度位置的爆破振动速度,爆破振动速度表现出“鞭梢效应”,并提出了预测振动速度更为精准的修正萨道夫斯基公式,对振动控制有着参考意义。研究表明:在矿山法掘进爆破中设置合理的掏槽方案和延期时差,或者弱化爆破振动波的传播途径,均能在一定程度上控制振动危害效应。
本研究结合巷道掘进生产情况,在工作面设置减振孔,通过弱化地震波的传播途径,达到了较好的降振效果。依据实际工程建立了不同减振孔参数的数值计算模型,分析各个模型的振动速度变化规律,最后结合实际工程数据进行对比分析,所得结果可以直接在实际工程中应用,例如:可以根据被保护构筑物的振动速度限值,选取减振效果最佳的减振孔参数,有助于避免根据经验盲目开挖造成成本的增加,对于实际工程中合理布设减振孔有一定的参考意义。
1 数值模拟
1.1 工程背景
研究区为深圳市城市轨道交通6号线二期工程6111标一工区。本研究选择深圳北站—梅林关区段进行相关分析。该区段单洞单线从新增竖井出发,全长200 m,埋深为23.5~38.5 m,隧道右线暗挖边线为书香大厦(图1),保安室为混凝土圈梁,建筑为钢结构板房,隧道顶与保安室间的夹持地层为微风化花岗岩。深圳北站—梅林关区段隧道洞身主要穿越的岩层为微风化花岗岩、中风化花岗岩。
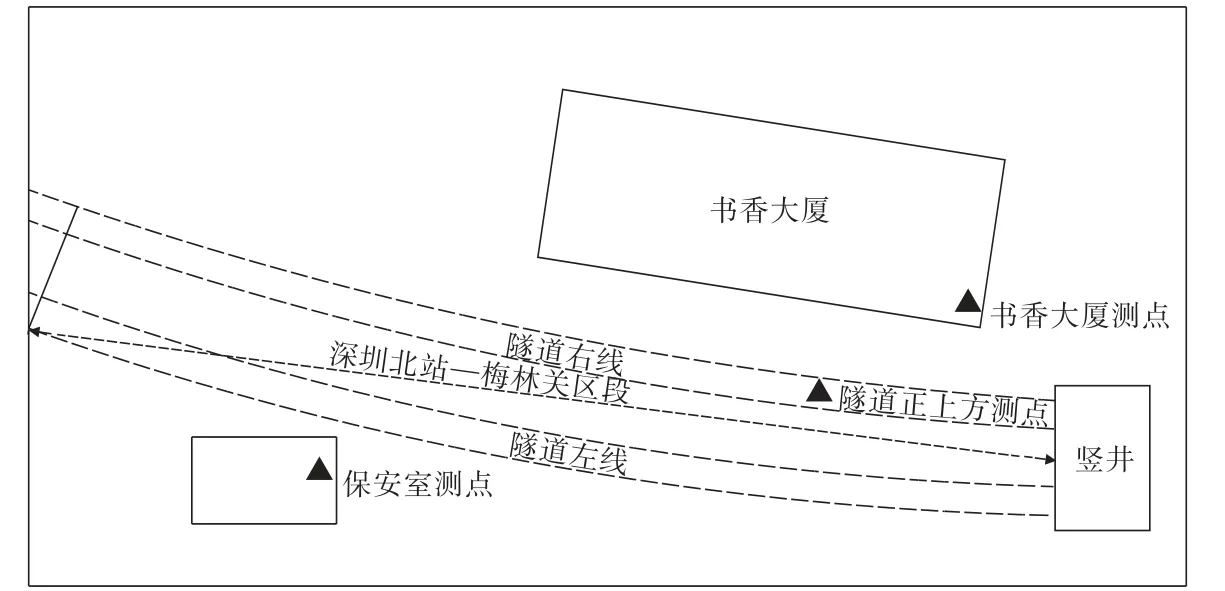
图1 深圳北站—梅林关区段示意Fig.1 Schematic of Shenzhen North Railway Station-Meilin Pass
1.2 岩土体—爆源—减振孔计算模型
本研究借助MIDAS/GTS NX有限元模拟软件建立“岩土体—爆源—减振孔”三维数值计算模型。数值模拟边界范围采取隧道洞口的3~5倍[7],隧道埋深为30 m,掏槽孔深1.3 m。为了减小模型尺寸对计算结果造成的误差,同时考虑到计算机的计算能力,综合考虑后模型尺寸为70 m×60 m×60 m(长×宽×高),线性时程分析总分析时间0.1 s,时间间隔为0.01 s,总步骤为100步,模型共有277 545个单元。本构方程选择摩尔-库伦准则,并且在数值模型边界上的每个节点处增加各自独立的地面曲面弹簧,以此来模拟实际岩土体的弹性边界,数值计算模型中选取的地层如图2所示,减振孔孔径、减振孔距爆源的距离、减振孔孔缘距(即相邻减振孔边缘最小间距)、减振孔孔深和双排减振孔间距如图3至图7所示。

图2 不同土层下的数值计算模型示意Fig.2 Schematic of numerical calculation model under different soil layers
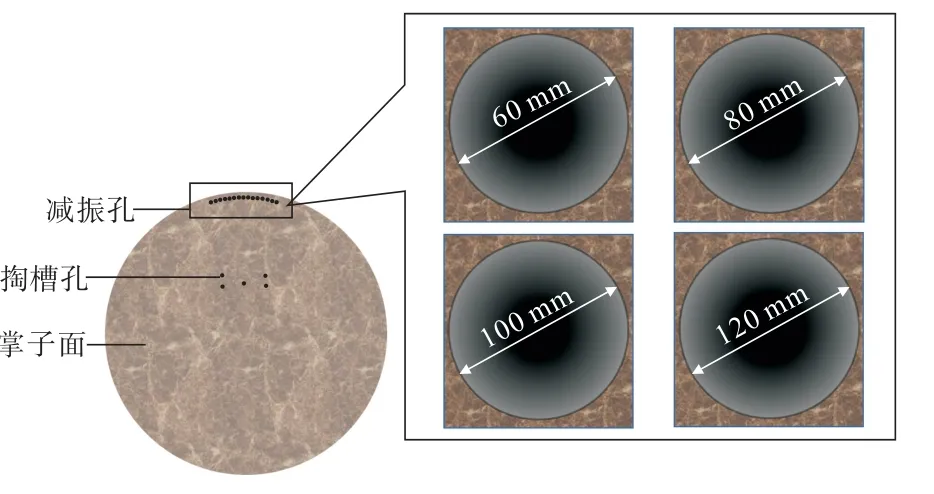
图3 工作面中减振孔孔径示意Fig.3 Schematic of the diameter of the damping hole in the working face
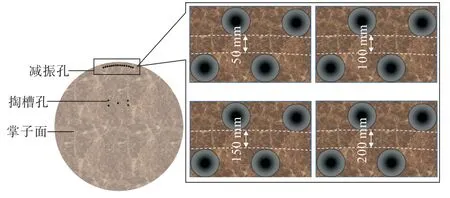
图7 工作面中双排减振孔示意Fig.7 Schematic of double-row vibration-damping holes in the working face
1.3 特征值分析
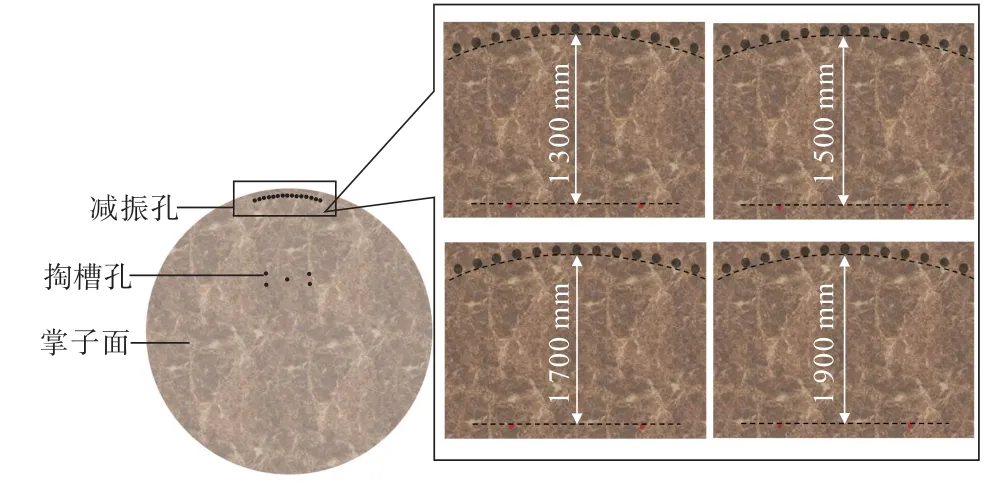
图4 工作面中减振孔距爆源的距离示意Fig.4 Schematic of the distance between the vibration damping hole and the explosion source in the working face
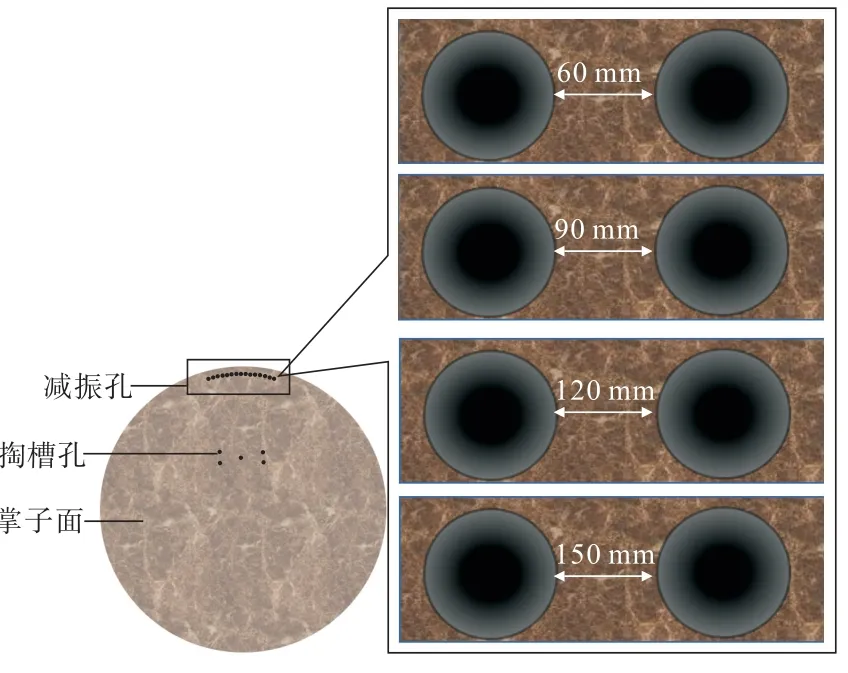
图5 工作面中减振孔孔缘距示意Fig.5 Schematic of the edge distance of the vibration damping holes in the working face

图6 工作面中减振孔孔深示意Fig.6 Schematic of the hole depth of the vibration damping hole in the working face
MIDAS/GTS NX数值模型分析过程中,在动力时程分析之前要进行特征值分析,并且结合结构的自振特性,对结构本身固有的动力特征进行初始分析。对数值计算模型的特征值进行分析,能够得出结构的振型、自振频率、质量和刚度等特性[8]。综合考虑各因素,最终确定本研究模型采用直接积分法对结构的动力响应进行分析,并且通过对数值模型的特征值分析得出建筑物的两大主振周期分别为1.094 4、1.089 3 s,其所对应的质量参与系数分别为28.21%和32.12%,得出的自振频率处于《爆破安全规程》(GB 6722—2014)规定的频率范围,因此文中对此不再讨论,只进行幅值和振动速度的讨论。
中国古典艺术批评“微妙”原理,既然源于中国古典艺术创作、品评的厚实活泼经验(包括对中国古典汉语细腻、温柔、婉转的创作经验,即评论像诗一样创作),粘泥着杂花生树的感知经验,看似零碎、漂浮、闪烁、偶然、感性,那么其具有通达与显现艺术普遍性真理的效力吗?
1.4 爆破荷载的施加
本研究利用MIDAS/GTS NX软件自带的动力荷载数据生成器获得的最终荷载曲线如图8所示。
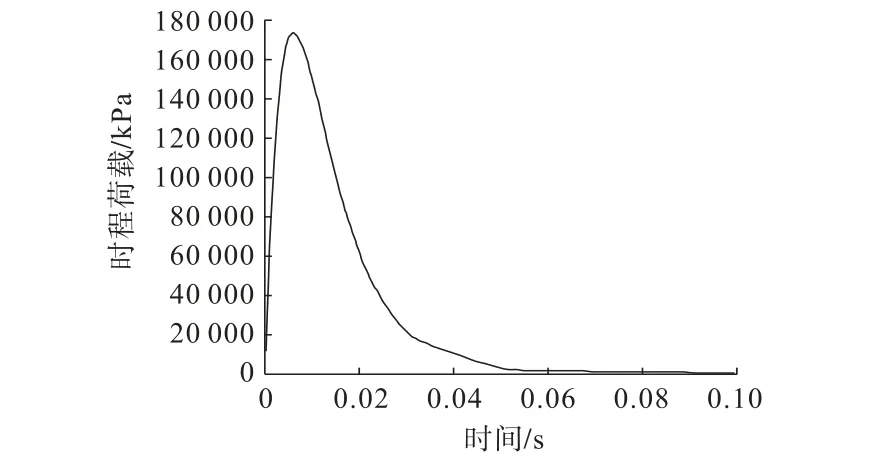
图8 爆破时程荷载曲线示意Fig.8 Schematic of blasting time history load curve
1.5 数值计算模型的可行性验证
根据已有研究[9-10],在实际工程中可采用垂向振动速度代替三矢量振动速度,简化控制标准,因此本研究只选用Z方向进行分析,具体监测数据和数值模拟结果见表1。由表1可知:除了隧道正上方测点Z方向的峰值振动速度外,其余所有测点的数值模拟结果均大于现场监测数据。出现这一现象的原因是数值模型在复杂地质条件下进行了很大程度的假设和优化。例如,地下岩石的裂隙以及地层都做了各向同性假定,同时也忽略了地下水的影响。表1中现场监测与数值模拟结果的误差都在10%以内,保证了数值计算很好地还原了现场实际情况,保证了数值计算结果的准确性。

表1 监测数据与数值模拟结果对比Table 1 Comparison of the monitoring data and numerical simulation results
1.6 数值模拟结果分析
在1.5节分析和实际数据分析的基础上,得到了5个因素Z方向的峰值振动速度见表2,测点位置如图1所示。由表2可知:未设置减振孔的工作面,其峰值振动速度均高于有减振孔的工作面,可见设置减振孔能够有效地降低峰值振动速度。
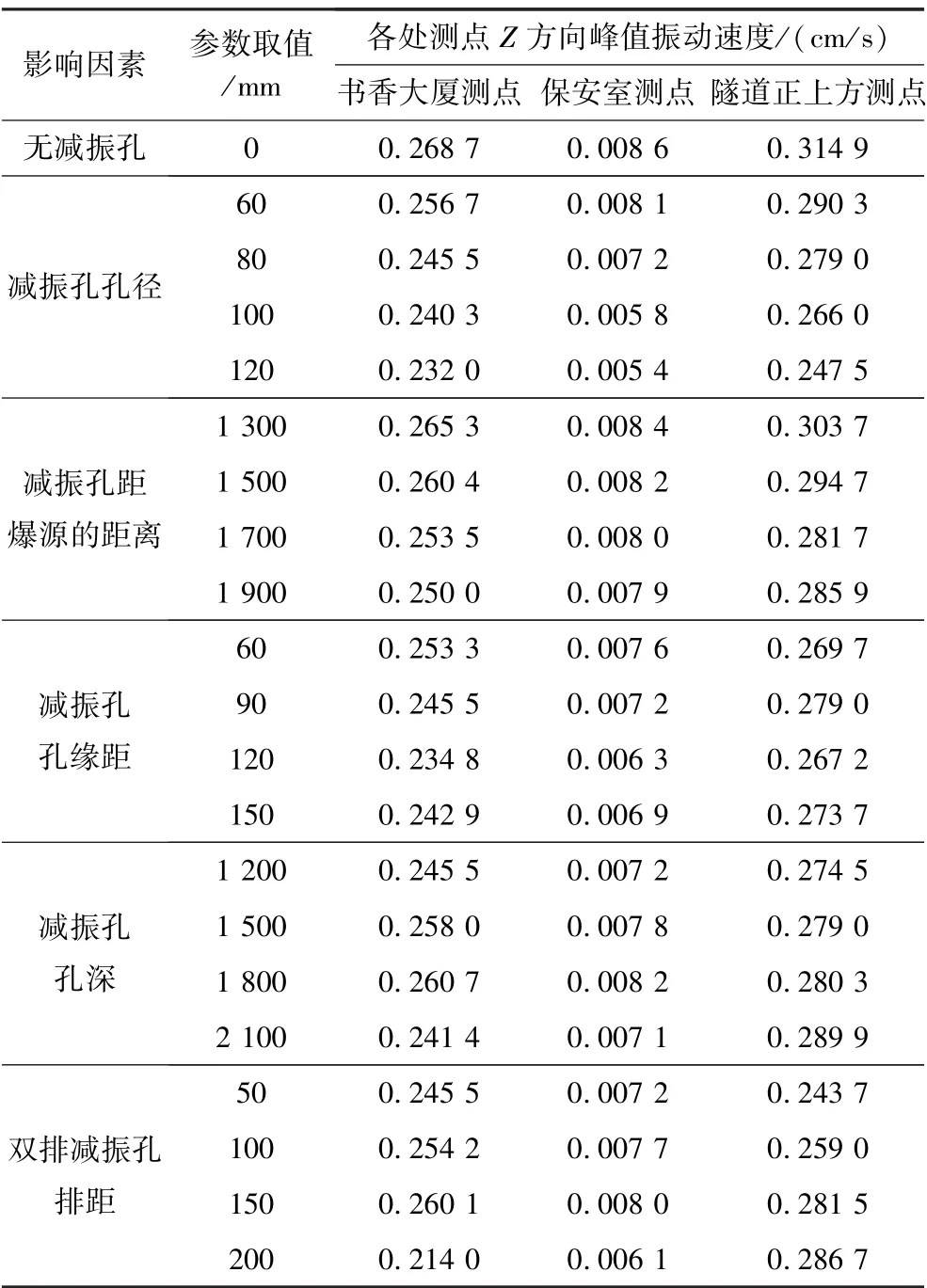
表2 各影响因素Z方向峰值振动速度Table 2 Peak vibration speeds in the Z direction of each influencing factor
根据21组数据形成了5组曲线,并且选择振动速度大和误差小的隧道正上方测点来分析振动速度的变化,振动速度随减振孔参数的变化曲线如图9、图10所示。
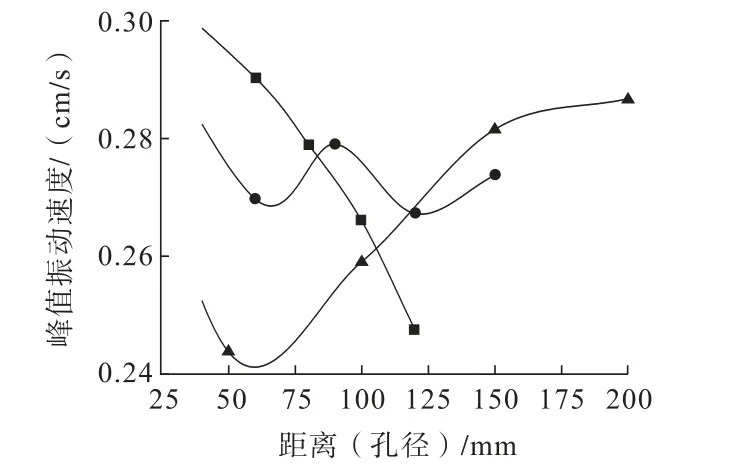
图9 减振孔孔径、减振孔孔缘距和双排减振孔排距对峰值振动速度的影响Fig.9 Influence of vibration damping hole diameter,damping hole edge distance and double row damping hole row spacing on the peak vibration velocity
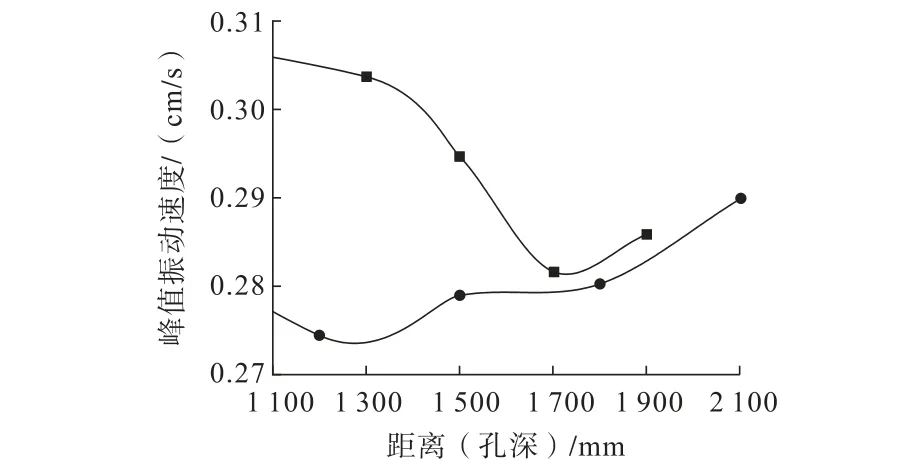
图10 减振孔距爆源的距离和减振孔孔深对峰值振动速度的影响Fig.10 Influence of the distance of vibration damping hole from the explosion source and depth of the vibration damping hole on the peak vibration velocity
分析图9可知:
(1)随着减振孔孔径不断增加,峰值振动速度不断降低,说明孔径的增加存在减振的效果,从降低的幅度中能够发现减振孔孔径大于120 mm时斜率较大,振动速度将不断降低,因此在工程中可以布置较大孔径的减振孔。
(2)减振孔孔缘距的测点曲线变化较大,峰值振动速度随着孔缘距的增大呈波动变化,在120 mm处出现最低振动速度,60~90 mm处也存在峰值,在150 mm以后开始上升,可见孔缘距的变化会出现较为复杂的振动速度变化,因此该因素会对峰值振动速度有较大影响。
(3)双排减振孔随着排距的增加峰值振动速度先降低后增加,在50 mm左右处出现最低振动速度,之后曲线在200 mm左右处呈平缓趋势,150 mm以后峰值振动速度变化较小,继续增加排距,振动速度变化较小,50 mm的排距在实际工程中很难实现,因此选择50~100 mm排距较为合适。经过分析可知,该因素的改变不会对振动速度产生较大影响。
由图10可知:
(1)峰值振动速度随着减振孔与爆源的距离的增大总体呈下降趋势,而隧道正上方测点在1 700 mm左右处出现最低峰值振动速度,由此可见对于该因素存在一定的阈值,并非越靠近爆源越好,建议在1 700 mm左右设置减振孔。
(2)孔深在1 300 mm左右时,振动速度达到最低,之后随着孔深的增加,峰值振动速度不断上升,且上升的势头没有降低。主要是由于减振孔孔深增加,会出现一定的空洞效应[11],从而使振动速度上升。
2 减振孔参数对减振效果影响的灰色关联度分析
2.1 灰色关联度分析原理
本研究运用灰色关联度分析方法讨论5种减振孔因素影响振动速度的敏感度,分析不同因素对振动速度影响程度大小,据此判定哪一种影响因素最能影响振动速度。该方法可用于判定相关因素的相关程度大小,可以在少数据、少信息和关系不明确的条件下,针对相关因素与比较因素有参考、有测度地分析,进而判断二者的相关程度。灰色关联度分析理论是灰色系统理论的重要组成部分,关联度表征参考因素与影响因素的相关性大小,相关性越大则关联度数值就越大,该影响因素对于比较因素而言越敏感[12-14]。
设影响减振效果的因素为相关因素变量,Z方向峰值振动速度为系统特征变量,由于各数列各因素的量纲级不同,关联信息分散,所以需要将相关因素变量和系统特征变量进行无量纲化[15-16],方可进行整体上的对比分析。对于无量纲化后的数据进行正负相关因素的转化,将负相关转化后的无量纲数据进行始点零化像计算[17],并将始点零化后的无量纲数值代入灰色绝对关联度公式,得到:
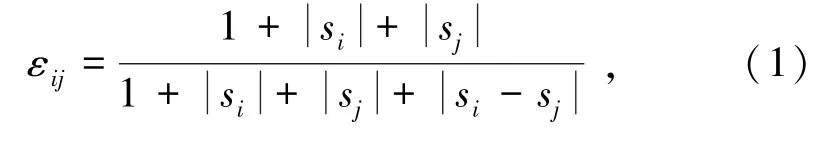
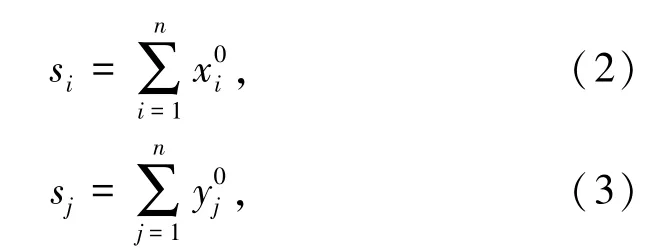
上述计算所得的灰色绝对关联度数值中,若有任意列的各行数据同时大于所有列,则该列所对应的因素为最优因素;若有任意行各列的数据同时大于所有的列,则该行所对应的特征为最优特征;若均不存在,则可使用其平均值作为关联度。
2.2 减振孔减振效果影响因素灰色关联度分析
根据数值试验计算结果,各影响因素的相关因素变量和系统特征变量取值见表3。
根据灰色关联度原理及相关计算步骤,通过表3中的数据可得灰色绝对关联度如表4所示。
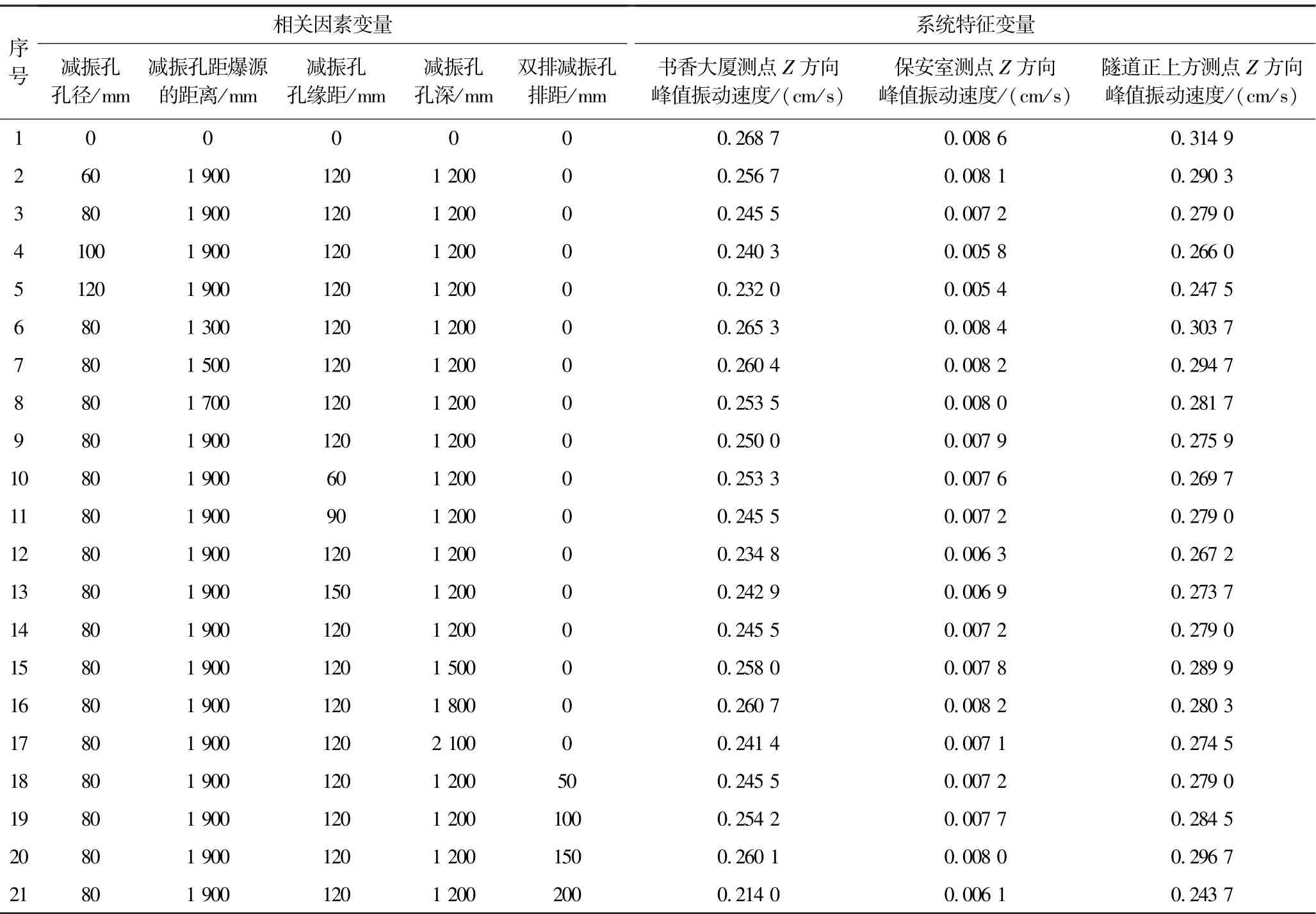
表3 相关因素变量和系统特征变量Table 3 Correlation factor variables and system characteristic variables
表4对应的灰色绝对关联度矩阵A为
表4 灰色绝对关联度分析结果Table 4 Results of gray absolute association analysis

2.3 结果分析
在矩阵A中发现第3列中的数据同时大于各列,所以与第3列对应的减振孔孔缘距为最优因素,减振孔孔缘距对减振效果的影响最为显著。
通过矩阵A还能看出与第1列和第2列对应的减振孔孔径和距爆源的距离的敏感度明显高于第4列和第5列,因此减振效果主要与减振孔孔缘距、孔径和距爆源的距离有关,其中,减振孔孔缘距对减振效果的影响最大。综合分析可知:各参数影响减振作用的主次关系为:减振孔孔缘距>减振孔距爆源的距离>减振孔孔径>减振孔孔深>双排减振孔排距。
2.4 工程实例对比
通过灰色关联度分析,发现减振孔孔缘距、距爆源的距离和孔径对减振效果的影响较大,但是还需要通过实例来进一步讨论这一结论的准确性。依据1.1节的工程背景,通过改变5种影响因素,来反映减振效果的大小以及验证分析结论的准确性。
通过图9、图10能够发现,峰值振动速度的上下幅度能够很好地反映减振效果,因此本研究引入减振率η这一指标来反映减振幅度,公式为

式中,η为减振率,%;v1为无减振孔时的测点振动速度,cm/s;v2为有减振孔时的测点振动速度,cm/s。
为避免离爆源越远振动速度越小且减振率变化越大的影响,因此去除保安室测点;由于距离爆源较近,振动速度较大会使减振率很小且减振率变化较小,因此去除隧道正上方测点,最终选择书香大厦测点进行分析。
在工程实践中减振孔参数依照1.2节所示进行布置,现场减振孔和炮孔布置如图11所示,现场实测数据和减振率数据见表5,各因素的减振率曲线如图12、图13所示。
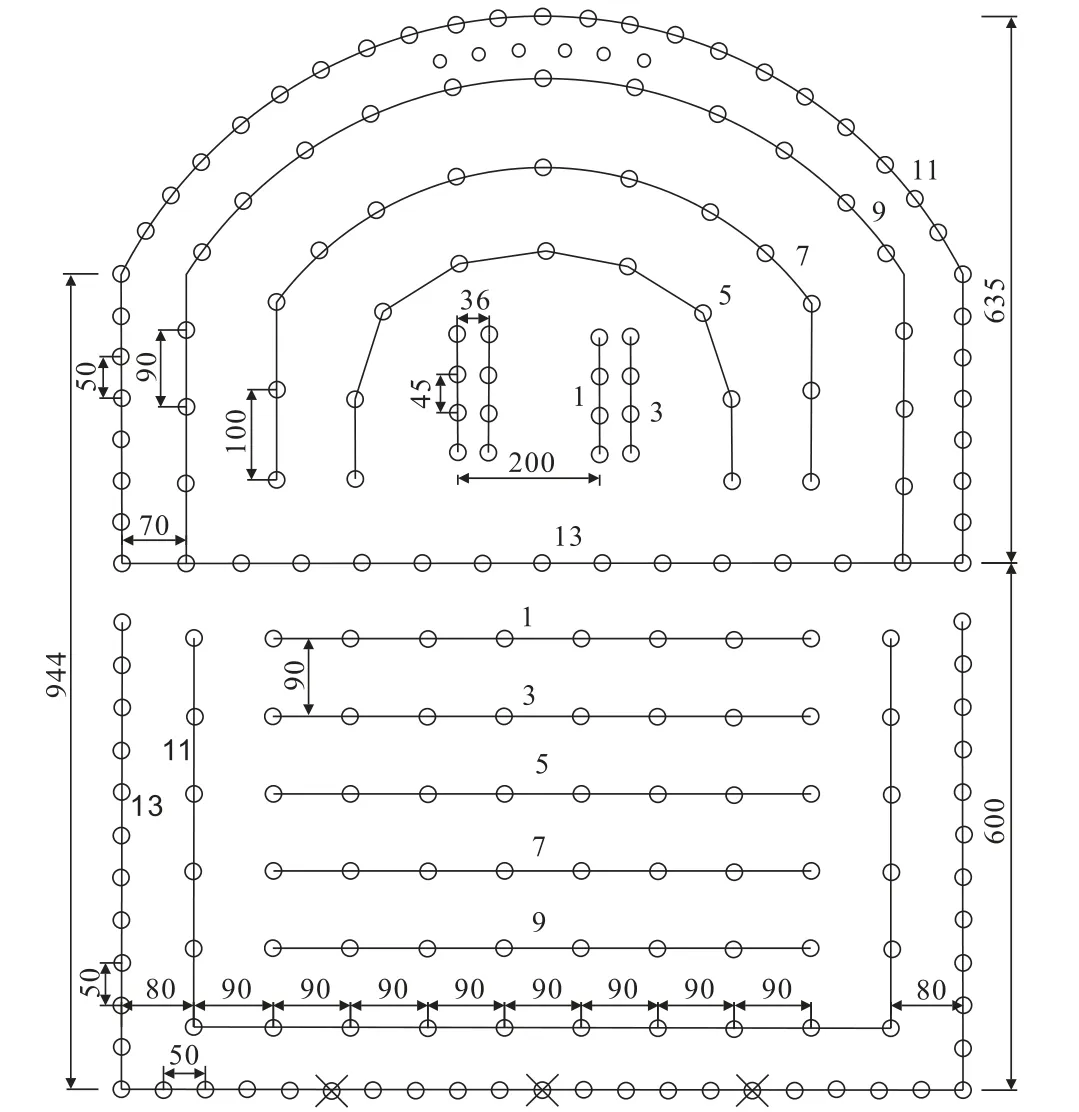
图11 现场减振孔和炮孔布置示意(单位:mm)Fig.11 Schematic of the layout of vibration damping holes and blast holes on site
由表5、图12和图13可知:通过改变每个参数大小,减振率均有较大变化。减振孔孔径的减振率最大变化为16.7%;减振孔距爆源的距离的减振率最大变化为17.0%;减振孔孔缘距的减振率最大变化为22.4%,减振孔孔深的减振率最大变化为10.6%;双排减振孔排距的减振率最大变化为14.9%。结合1.6节的分析,虽然孔深和双排减振孔排距的减振率也有较大变化,但不适用于该工程。综合比较减振率,其中减振孔孔缘距的减振率最大,对减振效果的影响最大,这也符合2.3节的分析结论。
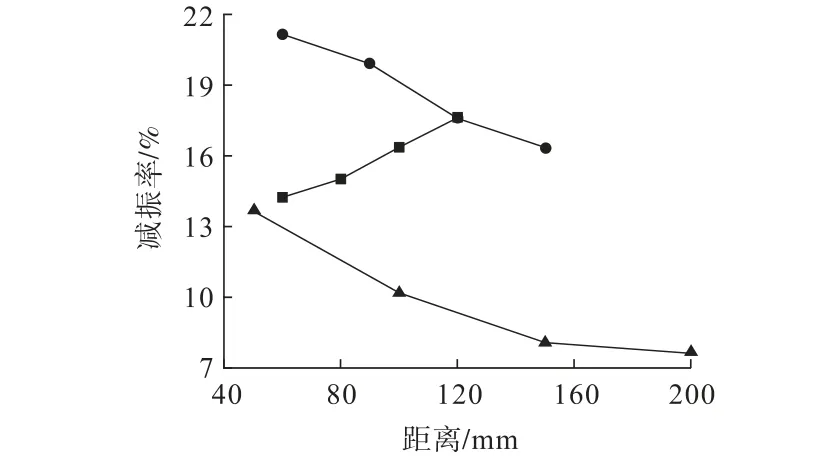
图12 减振孔孔径、孔缘距和双排减振孔排距的减振率随距离变化曲线Fig.12 Variation curve of damping rate with distance of damping hole spacing,hole edge spacing and double-row damping hole spacing
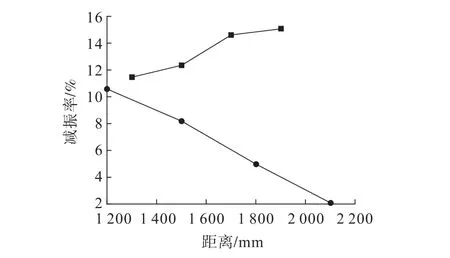
图13 减振孔孔深和距爆源的距离的减振率随距离变化曲线Fig.13 Variation curve of damping rate with distance of damping hole depth and distance from explosion source
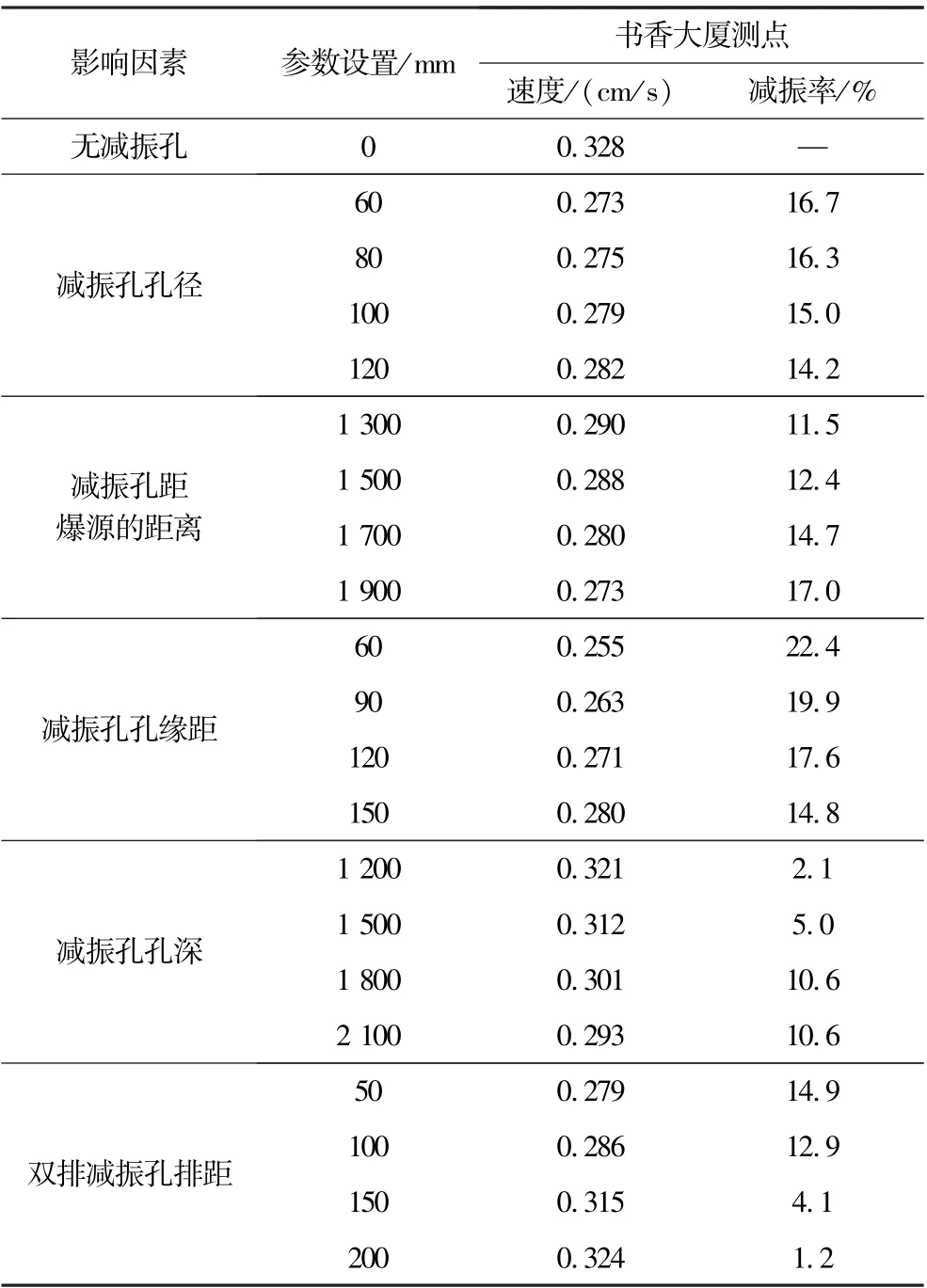
表5 现场实测数据和相应减振率Table 5 Field test data and corresponding damping rates
进一步分析图12和图13可知:减振孔孔径的减振率增长幅度较大,减振率呈不断上升趋势,与图9减振孔孔径所示特征一致;减振孔孔缘距的减振率最大,总体变化较为明显,符合上述多条分析结论;双排减振孔的减振率变化较大,总体的减振率较低,且随着距离的增加减振率降低较少,与图9双排减振孔排距所示特征一致;减振孔距爆源距离的减振率总体较为平滑,减振率变化较小,符合图10减振孔距爆源的距离的变化规律;减振孔孔深的减振率总体变化较大,符合图10减振孔孔深的分析结果。
3 结 论
(1)在掘进工作面直接设置减振孔,在一定程度上弱化了爆破振动波的传播途径,能够较好地降低振动危害效应。运用灰色关联度理论,对爆破工作面减振孔参数的减振作用进行了分析,得出各参数减振作用的主次关系:减振孔孔缘距>减振孔距爆源的距离>减振孔孔径>减振孔孔深>双排减振孔排距;与普通爆破方案相比,采取减振孔后现场减振率最高可达到22.4%。
(2)结合深圳地铁6号线深圳北站—梅林关区段隧道爆破方案及实测数据分析,发现减振孔孔缘距选择120 mm,减振孔距爆源的距离选择2 000 mm,减振孔孔深选择1 200~1 500 mm,双排减振孔交错布置,排距选择50~100 mm时,能够取得较好的降振效果。
(3)本研究仅对单一减振措施进行分析,且只采用改变单一变量的研究方法,而实际工程的现场情况比较复杂,只改变单一因素比较困难,因此下一步将进行多减振孔参数以及多种减振方式的综合研究。

