管廊燃气爆炸载荷特征及作用效应研究

钟冬望 李腾飞 何 理,3 杨志龙 陈江伟

(1.武汉科技大学理学院,湖北 武汉430065;2.湖北省智能爆破工程技术中心,湖北 武汉430065;3.江汉大学爆破工程湖北省重点实验室,湖北 武汉 430056;4.中国建筑第七工程局有限公司,河南 郑州 450004)

管廊内部包含燃气管道、电力管线、自来水管道 等各种能源管线，是城市正常运行的重要保障。燃气发生泄漏和爆炸的事故时有发生，严重威胁着城市安全和居民的生命财产安全。由于燃气爆炸的破坏效果受到浓度[1]、点火能[2]、点火位置、结构类型[3]等因素的影响，管廊内燃气爆炸超压传播和破坏效应与常见的街道燃气偶然爆炸相比要更为复杂。因此对管廊燃气爆炸仓内超压作用特性和过程进行研究具有十分重要的现实意义。

目前，国内外学者主要通过数值模拟方法对管廊燃气爆炸效应进行了探索研究[4]。刘希亮等[5-6]基于流固耦合和ALE多物质算法研究了燃气爆炸冲击波、不同截面形状对管廊结构的影响，并认为在爆源附近会形成负压区;王成等[7]通过小尺度管道试验研究了不同初始条件下甲烷—氧气混合气体爆炸火焰传播的规律;彭培等[8]对混凝土砌体墙在燃气爆炸荷载作用下的性能进行了研究，并结合LS-DYNA软件对砌体结构进行了简化模拟，并给出了砌体结构加固建议;孙加超等[9]同样采用LS-DYNA软件对管廊模型进行了燃气爆炸数值模拟，得到了仓内的超压时程曲线和管廊的破坏形式;陈长坤等[10]基于流固耦合算法对管廊在燃气爆炸荷载作用下的动力响应规律进行了探究。可见，LS-DYNA软件对于结构在燃气爆炸荷载作用下的动力响应过程模拟效果较好、应用广泛。对于燃气的泄漏过程一般采用Fluent、FLACS等流体力学数值模拟软件进行分析，例如，韩永华等[11]利用FLACS软件对燃气泄漏过程和爆炸效果进行了模拟，提出了提升空间爆炸安全韧性的防护措施，数值模拟软件的作用越来越显著，已成为科学研究的重要手段。

由于管廊结构尺寸大，且燃气爆炸不稳定因素较多，近年来，大型模型试验开展的较少[12]。BEAK等[13]分别进行了静力加载试验和气体爆炸试验，对比研究了气体爆炸荷载与静态荷载的作用差异。孙松等[14]搭建了2 m×1.2 m×0.6 m(长×宽×高)的爆炸容器，对不同浓度乙烯爆炸超压场进行了研究;张秀华[15-16]在大型核爆炸模爆器内对乙炔空气混合气体开展了结构抗爆的可行性研究，并利用数值模拟方法对TNT和燃气爆炸产生的冲击波载荷进行了对比分析。

综合上述成果分析发现，现有研究倾向于采用数值模拟方法进行燃气爆炸过程和结果的研究，成果虽然在一定程度上能反映燃气爆炸的作用效果，但在模型试验和现场试验等方面涉及较少。为此，本研究对管廊内燃气爆炸荷载特性进行理论分析，推导出管廊结构最大位移响应计算公式，通过模型试验得到管廊燃气仓爆炸超压场分布特征，并基于数值模拟结果与试验结果对推导的公式进行验证，为管廊燃气爆炸荷载作用研究提供一定的理论和试验依据。

1 燃气爆炸荷载作用下结构位移响应的理论推导

燃气爆炸荷载作用于管廊燃气仓壁面属于非周期激励的暂态响应，假设燃气仓壁面所受的爆炸荷载为P(t)，其运动学方程为

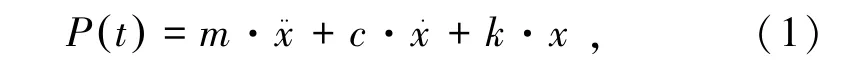
式中，t为时间，s;m为仓壁的质量，kg;为加速度，m/s2;c为粘性阻尼系数;为速度，m/s ;k为系统的刚度，N/m;x为位移，m。

在t=τ至t=τ+dτ的时间微元内，燃气爆炸荷载产生的冲量为P(τ)dτ，由冲量定理可得，燃气仓壁在冲量作用下导致的速度增量为

式中，Δv为速度增量，m/s。

因此燃气仓壁面产生的位移增量为

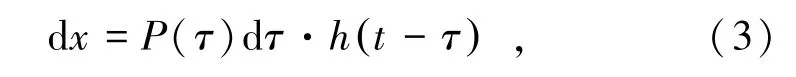
式中，h(t-τ)为用单位脉冲响应函数表示的瞬态响应过程，根据燃气仓壁面初始条件位移x(0)=0，初始速度(0)=，可以将h(t-τ)简化为无阻尼的保守系统下的单位脉冲响应函数h(t):

式中，自振周期ω=ωd=ωn，ωd为有阻尼固有频率，ωn为无阻尼固有频率;对于无阻尼的保守系统，阻尼比ζ=0。

根据线性系统的叠加原理，在零初始条件下引入Duhamel积分(式(5))，并将式(4)代入式(5)中，得到燃气仓壁面的位移响应函数x(t)(式(6)):

于是，式(6)可进一步化为:

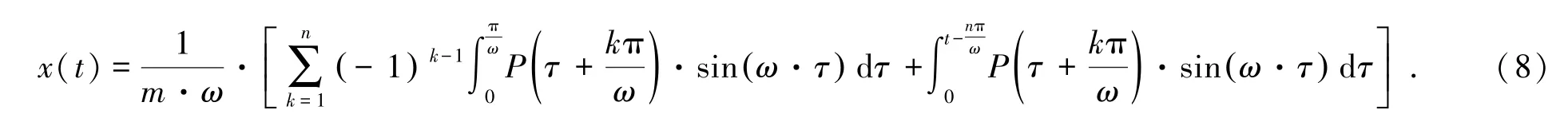
通过将燃气爆炸荷载作用下燃气仓壁的响应切分为(n+1)份，可将每一份都看作是一个冲量，则在前n份中每相邻的两个冲量之间的作用恰好相反。如图1中将经典燃气爆炸荷载切分成多个冲量，对于该种情况下应考虑极限情况，峰值处响应最不利情况为前n个冲量刚好相互抵消，而第(n+1)份恰好位于燃气爆炸荷载作用的峰值区域;峰值处响应最有利情况则是前n份冲量的作用并不能相互抵消。考虑燃气爆炸载荷变化较慢，第(n+1)份冲量最多有一半用来抵消前n份冲量的作用，因此管廊结构在燃气爆炸荷载作用下的最大响应为作用于结构爆炸超压峰值的0.5～1.0倍，考虑极限情况得到的最大响应峰值计算公式为式中，Pm为燃气爆炸荷载的压力峰值，Pa，Xm为管廊燃气仓壁的位移峰值，m。式(8)使用范围应满足爆炸荷载加载时程较长的特点。

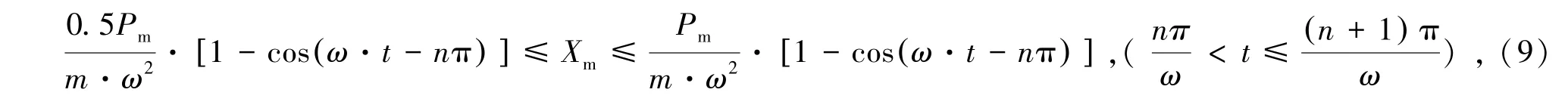
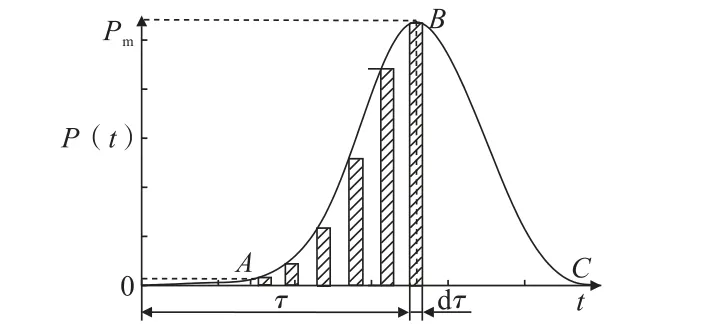
图1 经典爆炸压力—时程曲线Fig.1 Classical blasting pressure-time history curve

2 管廊燃气爆炸相似模型试验研究

2.1 物理模型制作及传感器布置

浇筑管廊实体结构的钢筋混凝土材料模型，模型整体呈长方体，长400 cm，共分3个仓室，上部仓室为通行仓，下部左右仓室分别为电力仓和燃气仓。其中，燃气爆炸主要发生在燃气仓中，试验布置及实体模型如图2(a)所示。模型截面尺寸为长170 cm、高210 cm，管廊内部用于隔离各个仓室的隔墙除了燃气仓与电力仓间隔墙壁厚为15 cm外，其余壁厚均为20 cm，各仓室的具体尺寸如图2(b)所示。

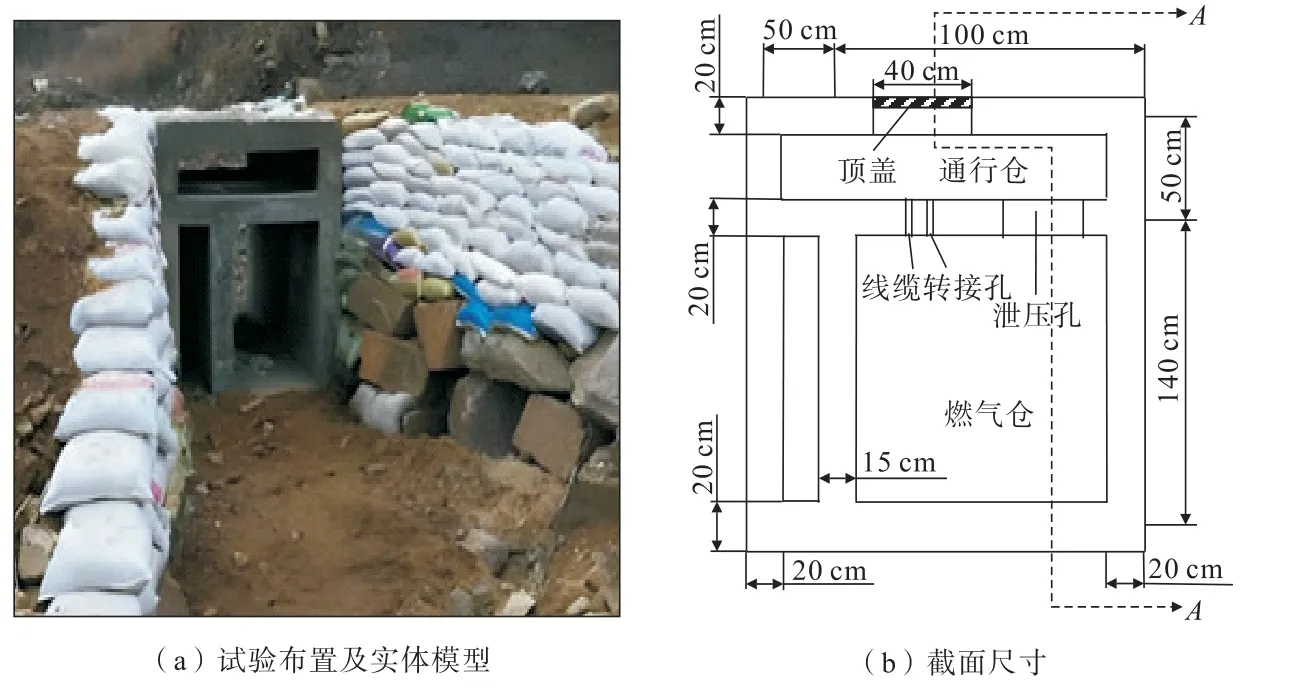
图2 综合管廊试验模型Fig.2 Experimental model of integrated pipe gallery

模型制作完成后，将开挖的土回填至与管廊顶部平齐，并通过振动捣实机压实管廊模型两侧回填区域，使周围土质情况复原，模型燃气仓轴向方向两端通过木板进行密封。

根据管廊模型的具体尺寸，在燃气仓内一共布置了4个壁压式冲击波传感器，传感器布置方案如图3所示，从管廊左侧仓门50 cm开始以75 cm为间距安装1#～4#壁压式冲击波压力传感器。

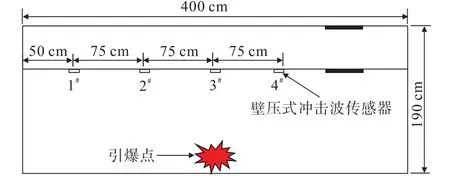
图3 压力传感器布置Fig.3 Layout of the pressure sensors

2.2 燃气充装与爆炸激发装置

通过如图4所示的天然气钢瓶及减压系统给管廊燃气仓充气，并在燃气仓两端使用搅拌装置加速气体的扩散运动，并将浓度检测仪置于浓度检测口中实时监测容器中燃气浓度，待达到燃气爆炸极限停止充气，测定燃气浓度稳定数值，重复前述步骤直至浓度示数稳定在试验设计浓度，立即对爆炸容器进行密封。通过无线遥控器远程控制对燃气仓内点火头进行通电，继而引爆仓内的燃气。

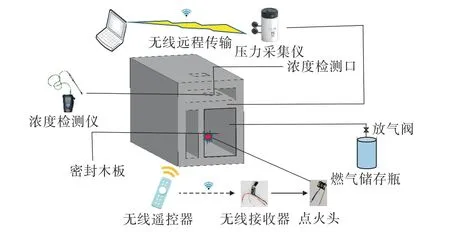
图4 物理模型试验系统Fig.4 Physical model test system

2.3 冲击波压力—时程曲线特征

相较于凝聚态炸药爆炸，可燃气体爆炸具有爆炸压力加载速率慢、峰值压力低的特点[17]，其升压时长可以达到数百毫秒，爆炸超压总作用时长可以达到秒级[18]。根据相关学者的研究，燃气爆炸的超压过程存在明显的3个阶段，在图1中OA段为缓慢升压阶段，AB段为快速升压阶段，BC段为压力下降阶段。由于压力传感器信号采集设备采用触发式采集方式，故而对OA段缓慢升压段未能完整记录。

在试验中采用薄木板与结构胶对管廊两端进行密封，以保证在起爆前气体不会发生泄漏，其抗压强度可以忽略不计，管廊内部的超压作用形式较为简单，与一般气体爆炸呈现的多峰值特性[19]不同。试验中选取的甲烷燃气浓度为9.5%和10%，浓度接近甲烷反应的最佳理论浓度，不会出现由浓度过低导致二次超压现象[20]。实测的超压—时程曲线见图5。

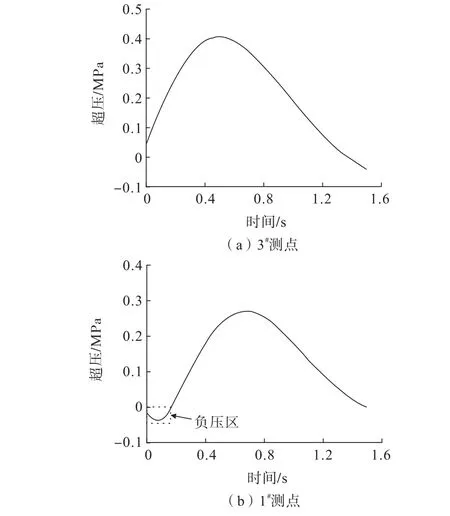
图5 典型超压—时程曲线Fig.5 Typical overpressure-time history curves

由图5可知:在爆炸超压作用下3#测点与1#测点的超压时程曲线反映出，爆炸超压的升压时长为500～700 ms，下降时长为900～1 100 ms。不同引爆方式对燃气爆炸的升压时长存在显著影响，根据文献[21]中的试验结果，在甲烷浓度为9.5%的情况下采用电火花引爆方式的升压时长为157.8 ms。本试验中的甲烷燃气爆炸升压时长要明显大于文献[12]中的结果，这是由于本试验模型尺寸大于前者，由于爆轰速度和模型密封性能等因素的影响，导致爆炸超压升压时长较大。

在1#测点的超压—时程曲线的初始阶段存在负压区，并且负压值在短暂增大以后超压便由负压转为正压。原因是:1#测点距离引爆点较远、靠近仓门，甲烷与氧气发生反应的初始阶段会快速消耗甲烷与氧气生成二氧化碳和水，反应产物在反应区域聚集来不及散开，导致燃气仓内气体分布不均，中心反应区压力升高而仓门等角落区域便形成负压，但该负压并不能使得仓门发生破坏，最终在反应生成高温高压气体后使得仓内超压将仓门推开，压力得到释放。

2.4 冲击波压力分布规律

管廊模型两端的木板在升压过程中在压力作用下脱落，形成了半自由空间的甲烷燃气爆炸模型，该模型下管廊燃气仓内壁的压力峰值分布特征如图6所示。根据理论计算及已有试验结果[22-25]，分析发现甲烷燃气爆炸破坏最不利结果浓度为9.5%。因此设置了甲烷浓度为9.5%和10%两种浓度梯度试验，并利用图4所示的燃气爆炸试验系统进行了现场试验。试验发现:对照组试验中爆炸超压峰值存在一定差异，其原因可能是管廊燃气仓内部体积较大，浓度分布并不十分均匀，但对照组试验结果仍在试验误差的允许范围内，并未改变超压峰值的传播和分布规律。

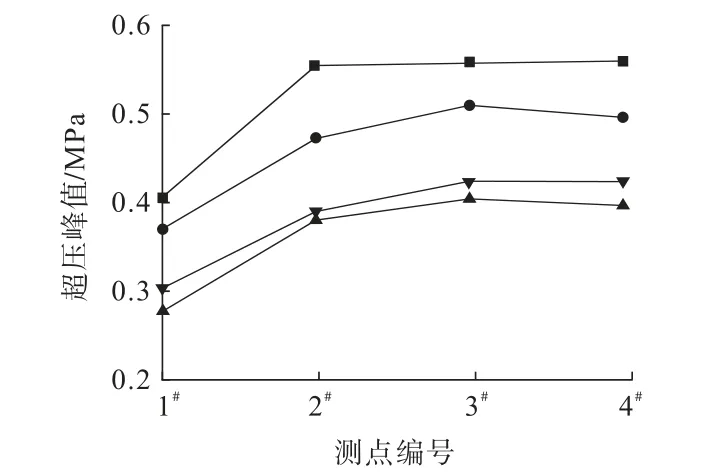
图6 各测点的超压峰值分布特征Fig.6 Distribution characteristics of peak overpressure at each mnoitoring points

由图6可知:甲烷燃气爆炸产生的壁面超压峰值分布规律与点源爆炸特征[26]存在一定的区别，燃气爆炸主要表现为压力波，没有动压力作用的方向性，距离引爆位置最近的3#测点壁面超压峰值在两种甲烷浓度下仅略大于两侧的2#和4#测点，说明引爆位置对管廊内超压峰值的分布影响有限，管廊内燃气爆炸载荷可以近似看作时变均布载荷。根据图5中的超压峰值结果，在甲烷燃气浓度为9.5%的情况下，两次对照试验中的最大超压峰值出现在2#和3#测点，峰值分别达到了0.56 MPa和0.52 MPa，在浓度为10%的情况下，最大超压峰值均位于3#测点，分别为0.41 MPa和0.45 MPa。对两种浓度的甲烷燃气爆炸超压对比可以明显看出，9.5%的甲烷燃气浓度发生爆炸会产生更大的超压。与受限空间内气体爆炸超压峰值基本相等略有区别[19]，在半自由空间中两种浓度的爆炸超压在管廊内传播过程趋势一致，在左侧仓门附近均存在明显衰减，原因是密封的木板被掀开，仓门附近的燃气和气压溢出。

3 燃气仓顶板位移值计算

3.1 模型验证

通过Ansys/Ls-Dyna数值仿真软件对管廊在燃气浓度为9.5%工况下的爆炸过程进行模拟分析，采用等效内能法将燃气爆炸荷载直接作用于管廊燃气仓内壁上，管廊模型按照与试验模型1∶1建立，如图7所示。

图7 管廊数值模型Fig.7 Numerical model of pipe gallery

为了对数值模拟结果的正确性和合理性进行验证，以管廊燃气爆炸试验中的空气冲击波压力峰值为参考，在相同测点位置读取数值模拟结果中的压力峰值，并进行了对比分析，结果见表1。

由表1可知:数值模拟结果略大于试验测得的数据，在实际试验中由于燃气混合不可能处于理想状态，而且数值模拟未考虑热力等效应，模拟结果除了在1#测点处的误差较大外，其余3个测点的模拟值均能够满足精度要求。1#测点超压峰值误差较大的原因在于模拟过程处于理想情况，并未顾及燃气爆炸过程中仓门被冲开、燃气和仓内压力在仓门附近被泄露等情况。因此，在仓门附近的1#测点模拟结果高于试验测得的超压峰值。

表1 模型试验与数值模拟各测点超压峰值Table 1 Model test and numerical simulation of the peak overpressure at each measuring point

3.2 模态分析

由于燃气爆炸荷载直接作用于综合管廊燃气仓壁，因此根据式(8)对上述关系进行验证。首先对部分参数进行求解，燃气仓上部墙体为两边固支，并且中间带空孔的混凝土板，求其固有频率过程需解超越方程。因此，本研究采用数值模拟求该混凝土板的各阶模态，计算得到该板的一阶频率并作为固有频率，即ω=690.16 Hz，一阶振型如图8所示。

图8 燃气仓顶部隔墙一阶振型Fig.8 First-order vibration shape of the partition wall at the top of the gas silo

3.3 最大位移响应对比

根据燃气仓顶部混凝土墙的材料参数计算得质量 ，将各测点的超压峰值代入式(8)，计算得到各测点处的最大位移响应见表2。

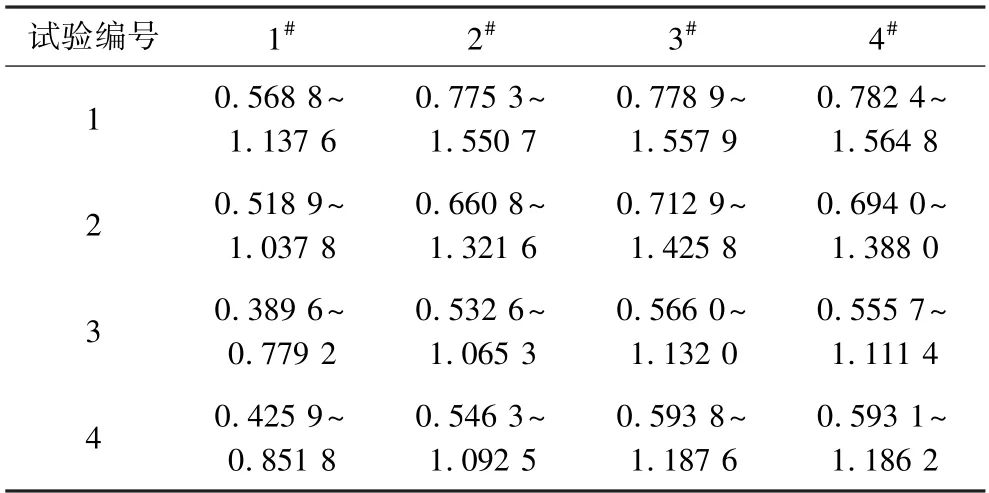
表2 各测点理论最大位移响应Table 2 Theoretical maximum displacement response of each measuring point×10-3m

根据管廊燃气爆炸纵向位移演化云图(图9)分析可知，纵向位移主要发生在燃气仓的上下混凝土板上，且位移方向由燃气仓向外。

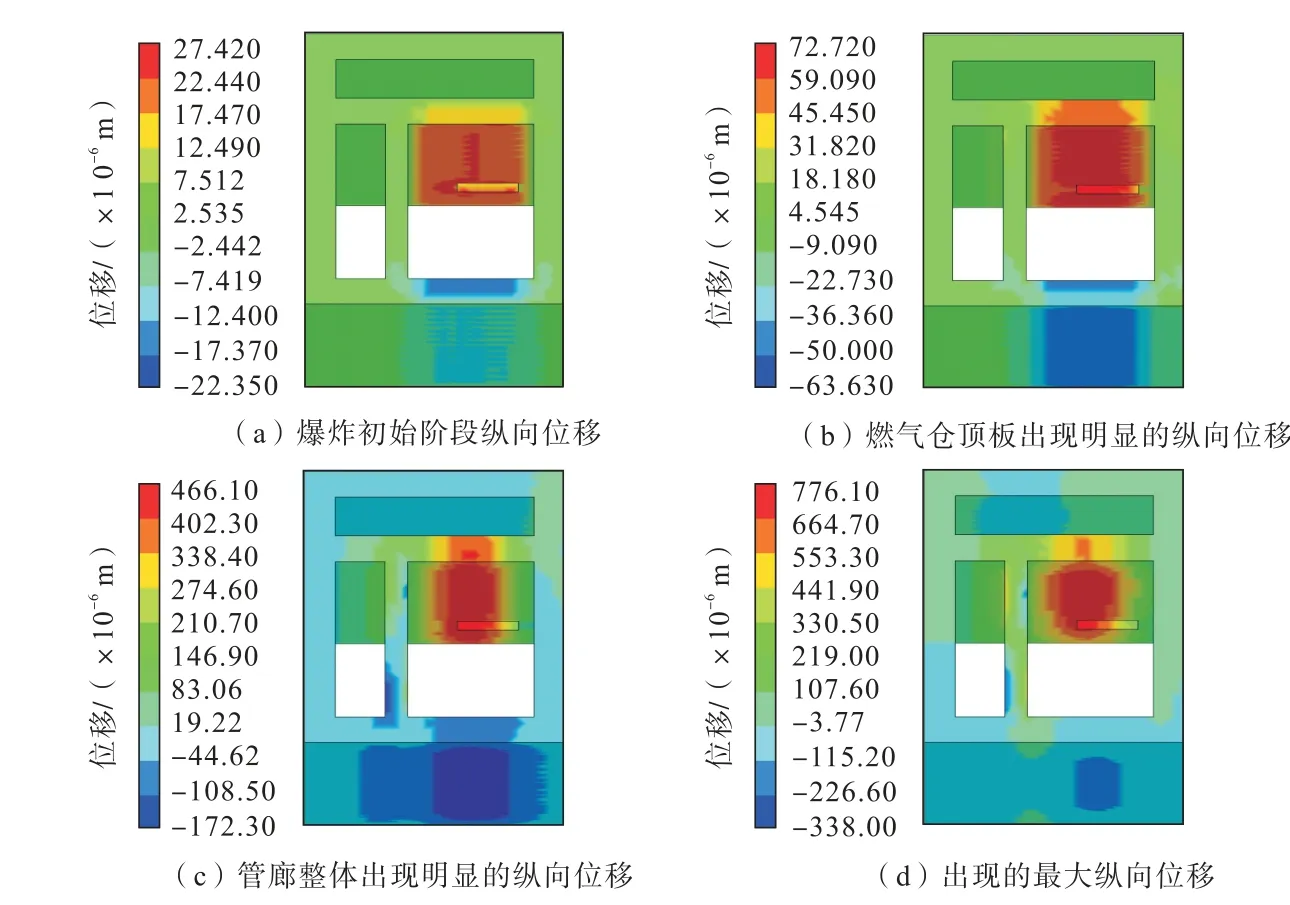
图9 纵向位移演化云图Fig.9 Nephogram of longitudinal displacement evolution

对数值模拟结果中的综合管廊模型燃气仓顶部进行取点，取点位置与压力传感器布置位置保持一致，获得了如图10所示的位移—时程曲线。分析图10发现，除了1#测点以外各点的最大位移较为接近，均在0.75×10-3m左右。

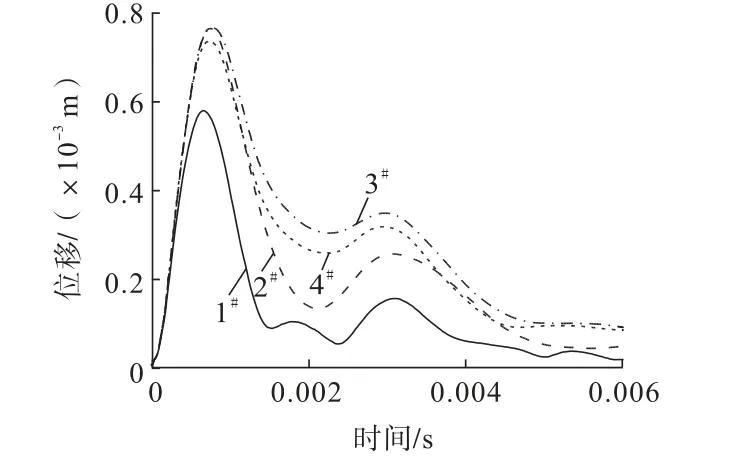
图10 燃气仓顶部测点位移—时程曲线Fig.10 Displacement-time history curves of monitoring points at the top of gas silo

将理论推导得出的综合管廊燃气仓顶部混凝土板的最大位移范围，与数值模拟得出的最大位移响应进行校核，得到如图11所示的位移对比图。

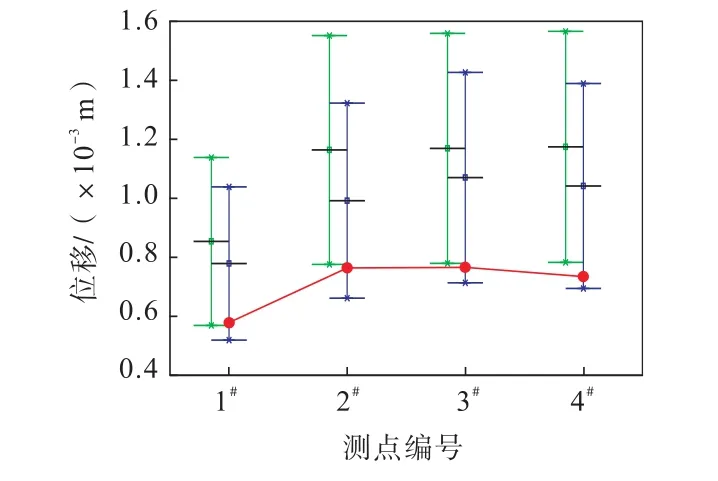
图11 理论位移与数值模拟位移对比Fig.11 Comparison of theoretical displacement and numerical simulation displacement

燃气仓顶部混凝土板数值模拟位移与理论结果吻合度高，在各测点采集到的最大位移全部位于理论最大位移范围内，且数值模拟位移响应变化趋势与试验结果一致，在1#测点处的最大位移均略小于其余测点。

4 结 论

针对甲烷气体爆炸压力加载较慢的特点，对管廊在燃气爆炸荷载作用下的动力响应进行了理论分析，并开展了燃气9.5%和10%两种浓度在管廊模型中的气体爆炸试验，综合理论推导和试验结果，得到以下结论:

(1)模型试验条件下，甲烷燃气爆炸超压—时程曲线呈单峰值状，超压升压时长500～700 ms，超压作用总时长达到1 500 ms左右，燃气爆炸超压作用时间与模型大小存在直接关系。

(2)甲烷燃气爆炸超压在管廊燃气仓内壁各测点的作用时程曲线大致相同，各处超压峰值基本相等，对管廊燃气仓壁面的作用可以近似看作时变均布荷载。

(3)推导得到最大位移响应计算公式，并经过了试验和数值模拟结果的验证，适用于燃气爆炸载荷作用下管廊的动力响应分析。