基于深度学习的信息高保密率传输方法
颜 祺 牛彦杰 陈国友
1(陆军工程大学指挥控制工程学院 南京 210001) 2(中国人民解放军94860部队 南京 210046)
随着5G通信技术的不断发展,多维度的万物互联和多用户的相互协调逐渐成为未来智能化世界的基础[1-3].在这种情况下,开放性的无线信道往往面临着被窃听的信息安全问题.而且,日趋复杂的电磁环境也使得通信终端很难通过传统的保密措施(如设计调制格式[4]等)来保证信息保密率[5-6].因此,研究新型的保密手段来保证通信过程中的信息安全性是一个值得关注的问题[7].
多维度的联合通信需要多方位的节点组成大型的多跳无线网络来保证信息的高效传输.为了满足在这种高复杂度大空间中的无线通信安全需求,有学者提出了利用译码转发的有源中继方法进行信息的无线传输[8-10].在此基础上,为了获得最优保密率,研究者们进一步针对中继选择系统的最大比值组合、分布式选择组合和分布式切换-停留组合方案进行了评估[11-12].然而,上述传统的路径选择方案缺乏全局的优化手段,而且耗时较长,难以同时满足高密度无线传输的信息安全性和实时性需求.近年来,新兴的深度学习技术有效解决了传统算法在全局优化与计算速度方面的问题[12-13],也为解决在无线网络中进行信息传输的安全性和实时性问题提供了较好的思路.
本文提出了基于深度学习的无线网络信息传输方案,以最大限度地提高信息在进行无线传输过程的保密率和运算速率.基于多次在不同环境下采集的无线通信数据和所有中继节点的信道状态信息(channel state information, CSI),通过人工神经网络(artificial neural network, ANN)实现对最优中继路径的选择,并研究了不同中继数量和窃听者位置对信息保密性能的影响.仿真结果表明,该方案的保密率性能与对所有中继选择组合进行穷举搜索所获得的保密率性能几乎相同.通过使用离线训练的模型,几乎所有的算法复杂度负担都在训练阶段执行.因此,复杂性只取决于分类阶段.利用本文方法可以指导无线网络规划员制定十分有效的网络结构,从而能同时保证信息传输的安全性与实时性.在平时进行无线中继网络搭建的过程中,大量搜集不同环境的CSI与无线通信收发数据,以此训练相应的模型,获得最优的参数,将复杂的运算过程灌注于平时.在实际应用环境中,可直接根据人工神经网络的输出结果进行无线网络的规划,达到安全高效的目的.
1 系统模型
无线网络系统模型由1个源节点S、1个目的节点D、DF可信的中继节点{Rn|1≤n≤Nr}和1个窃听节点E组成,其结构如图1所示.假设所有节点均配备单一天线,工作在半双工模式下,从S到D存在1条直连链路.下面着重介绍2种传输方案,即协同传输(cooperative transmission, CT)和2跳传输.
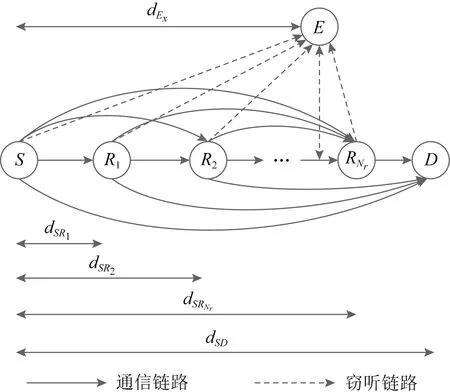
图1 系统模型
1.1 信息的协同传输方案
在该方案的设计中采用了多跳传输.因此,S和D之间存在Nr个中继节点,而且,信息传输是在(Nr+1)时隙中进行的.在第1个时隙中,S发射信号s,其功率为P0,信息传输的目标是所有的接收终端.此时,假设P0=P/2.因此,D处接收到的信号、第n个中继点接收到的信号、窃听者处接收到的信号分别为
(1)
(2)
(3)
其中,hSD为S-D链路的复杂信道增益,hSRn和hSE分别为S-Rn中继链路和S-E窃听链路的复杂信道增益.zD,zRn和zE是接收方差为δ2的加性高斯白噪声.
在下一个时隙,S与D中间的通信通过中继器正确解码信号s实现(这种中继器称为有源中继器).假设在所有Nr继电器中选择T≤Nr的有源中继器,并在时隙T中连续向D发送信息.因此,第m个时隙的D终端、第k个中继和窃听者E处的接收信号分别为
(4)
(5)
(6)
其中,m=1,2,…,T;k=m+1,m+2, …,T,Pm为第m个有源中继器的发射功率,hRmD,hRmRk,hRmE分别为第m个中继器与D之间的链路、第m个中继器与第k个中继器之间的链路、第m个中继器与窃听者E之间的链路的复杂信道增益.
设每个有源中继器的发射功率等于P1/T,其中P1为所有有源中继器的总发射功率,设P1=P/2.此外,假设所有接收机都采用最大比合并(maximum ratio combining, MRC)技术处理接收到的信号.因此,在时隙T+1中,终端D、窃听者E和第m个有源中继器收到信号的速率分别为
(7)
(8)
(9)
其中,

以上系统中可实现的保密率为
Γct=max{ΓD-ΓE,0},
(10)
其中,ΓD,ΓE分别如式(7)、式(8)所示.
为保证上述方案的可行性,需要检查有源中继器是否能正确解码来自S的信号,称为“DF中继约束”,如{ΓRm≥Γth|m=1,2,…,T},其中Γth为速率阈值.
当“DF中继约束”的条件不被满足时,则不能得到式(10)中的保密率.在Nr中继器中的T中继器被激活的情况下,可以考虑(T,Nr)的场景.考虑1≤T≤Nr,可能存在的中继选择场景个数为
(11)
其中,T!表示非负整数T的阶乘.对于每个场景,使用“DF中继约束”条件检查该场景的可行性,并计算保密率如式(10)所示.
假设本文方案中最高保密率为Γct,如式(10)所示.T=0表示采用直传方案(direct transmission, DT).在这种方案中,D处的速率和窃听者E处的速率分别可以计算为
(12)
(13)
那么,本文所提出系统的可实现保密率为
(14)
在无传输(no transmission, NT)方案中,可实现的保密率Γnt=0.本文的目标是在所有可能的中继选择场景中找到一个案例,以获得系统的最高可达到的保密率.那么,在该多跳DF中继网络中,使保密率最大化的中继选择问题可以表示为
Γs=max{Γnt,Γdt,Γct},
(15)
其中,Γdt,Γct分别如式(10)、式(14)所示,这个问题的解决方法可以概括为以下的“理论算法”:
1) 对于DT方案,计算保密率Γdt如式(14)所示;
3) 将式(15)代入所有保密率公式中,计算相应的DT和CT方案,选择保密率最高的方案.
1.2 信息的2跳传输(最佳中继选择)方案
该方案将2跳传输方案视为基线.选择一个满足“DF约束条件”的有源继电器,由辅助源向目标发射信号.此时T=1,信息以2跳方式传输.在第1跳中,信息从S传输到所选中继,在第2跳中,所选中继将接收到的信号解码后转发给D.
对于该方案,在2个时隙中D、窃听者E和第m个有源中继接收到信号的速率可计算为
(16)
(17)
(18)
其中,αRm,D=|hRmD|2,αS,Rm=|hSRm|2/δ2,P1=P0=P/2.则该方案的系统保密率为
(19)
其中,
(20)
式(20)为各有源中继器的保密率.那么,该方案中最大可达保密率的中继选择问题可表示为
(21)

在本研究中,假设在S有一个全局CSI.在实践中,接收用户(即E或D)估计并将来自S和所有中继的CSIs的绝对值反馈给S.当Nr中继存在时,每个终端用户发送Nr+1的CSIs绝对值作为反馈信息.
2 深度学习中继选择
2.1 生成输入数据
对于训练数据集,以此生成L个CSIs,并从这些CSIs中提取实值特征向量.然后对特征向量进行归一化处理.特征向量的生成方法如下:
步骤1. 生成第l个特征向量dl:
dl=
(22)
步骤2.使用步骤1为L个CSIs生成L特征向量.
步骤3.对特征向量dl进行归一化得到归一化向量zl.归一化向量zl的第n个特征元素可以计算为
(23)

2.2 标 签
选择式(15)所示的保密率作为关键绩效指标.从每个训练数据样本和关键绩效指标可以很容易地确定对应于当前样本的类标签.在S和D之间的通信过程中需要选择一种传输模式.类标号是包含由传输模式和中继选择组合的索引组成的重要信息的情况索引.一般情况下系统有Nr个继电器,采用P=2Nr+1类标号,其中2Nr个类标号用于继电器选择组合,1个类标号用于NT方案.表1给出的标签示例表明,当给定的CSI的类标签t=0时,选择NT方案.当t=1时,选择DT方案.当t=2时,系统执行CT方案.其中一个中继器有活动,其索引为第1个中继器,以此类推.
2.3 构建训练数据集
在生成输入样本和标记之后,将输入输出对连接起来,创建完整的训练数据集.
Dtrain={(z1,t1),(z2,t2),…(zL,tL)},
(24)
其中,ti是第i类标号.
2.4 网络结构设计
下面将描述如何用神经网络分类器解决中继选择问题.利用标记的训练数据集,构造训练好的神经网络模型.该模型的输入是CSI的绝对值,输出是所选中继器集的指标等重要信息,以及其中一种传输方案.所考虑的系统信息传输性能将选择DT,CT和NT这3种传输方案中的一种,本文介绍的神经网络其结构包含在每个隐藏层中的多个神经节点(称为神经元元).每一层的输出都经过一个称为“激活函数”的非线性函数.最常用的激活函数是整流线性单元(ReLU)函数,可以表示为
fReLU(x)=max(0,x),
(25)
其中,x是函数的参数.本方案选择的激活函数是ReLU,因为它可以帮助模型更快地收敛[29-30].在多分类的情况下输出层使用激活函数,可以表示为
(26)
其中,C是类的数量,i,j∈{1,2,…,C},xi,xj分别是第i类分数和第j类分数.
一般来说,这些层被安排在一个链结构,其中每一层是前一层的激活层,在这里将激活层表示为
o=f(z,w)=
f(k-1)(f(k-2)(f(k-3)(…f(1)(z)))),
(27)
其中,o,z,w分别表示神经模型的输出、输入和权值,k为神经网络的层数.
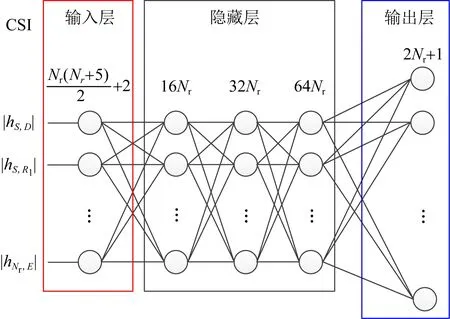
图2 ANN模型
如图2所示,本文设计了一个包含5层的网络,取CSIs的绝对值;第1隐藏层、第2隐藏层和第3隐藏层分别由16Nr个、32Nr个和64Nr个单元组成.输出层有2Nr+1个单元,对应2Nr类包含所有组合中继器选择案例的保密率值,有一类代表NT方案的保密率值.该层采用Softmax函数表示所有类的概率分布,得到概率值最大的最优类.该类提供了与给定CSI相对应的最佳中继器选择和NT方案.
对于任意规模的网络,神经网络模型由1个输入层、k≥1的隐藏层和1个输出层组成.输入层的元素个数等于所有节点的CSI总数Nr(Nr+5)/2+2,而第k隐藏层和输出层的神经元个数分别为2(k+3)Nr和2Nr+1.
2.5 ANN训练
下面将描述如何选择适当的参数训练神经网络.总共为训练数据生成65万个样本(即L=650 000).将训练数据集分解为训练集和验证集.用训练集训练网络参数,用验证集对训练后的模型进行评估.对于以上设计的神经网络结构,交叉熵可以作为ANN模型的损失函数.因此,每个第i个样本输入z(i)的损失函数可以表示为
Loss(t(i),o(z(i),w,b))=-lb(o(z(i),w,b)),
(28)
其中,t(i)为系统2Nr+1种可能情况中保密率最高的最佳传播情况的标号,o(i)(z(i),w,b)是神经网络预测t(i)的输出,权重值为w,偏差值为b.训练过程的目标是找到合适的参数w和b,使入口训练数据集的平均损失(称为“代价函数”)最小.代价函数定义为
(29)
其中,集合Θ={w,b}包含ANN模型的每个训练参数.每个参数通常使用梯度下降方法迭代更新.在每次迭代中,每个参数同时更新为
Θm+1=Θm-η∇ΘL(Θ),
(30)
其中,∇Θ表示为Θ的梯度算子,η为学习速率,m为迭代次数.本文提出的ANN模型采用了Adam优化算法,因为该算法只需要计算一阶梯度,从而降低了计算复杂度[14].此外,为了减少训练中的过拟合,将文献[15]中的dropout技术应用到神经网络模型中,本文选择10%作为dropout值.
训练过程结束后即可获得参数w和b,按系统配置,可以获得新的输入向量z,并计算出最高保密率.这意味着,任意1次通道变化都会获得1个新的z值,将这个z值应用到ANN中继续训练,而无需求解式(15)所定义的问题.
3 仿真结果
3.1 信息安全传输的模型假设
本文方法以保密率作为指标来评价系统的有效性.为了进行基准测试,将DT和2跳传输方案的结果与本文所提出的中继选择方法(CT方案)结果进行比较.此外,对于机器学习方法,将ANN模型与SVM模型的性能进行了比较.
其中S-D,S-Rn,S-E,Rn-D,Rn-E的距离分别表示为dSD,dSRn,dSE,dRnD,dRnE.假设S,Rn和D的位置在1条直线上,其结构见文献[15].假设所有通道都经历相同且独立的瑞利衰落分布,设置总发射功率P=30 dBm,噪声功率δ2=-30 dBm,路径损耗指数c=3.5,阈值速率Γth=0.1 b/(Hz·s-1).假设S和D分别位于(0 m, 0 m)和(0 m, 120 m)处,或dSD=120 m,所有中继节点位于S和D之间,中继节点距离为dSD/(Nr+1).假设当dEx沿S和D之间的平行线从50 m移动到180 m,dEy从5 m移动到10 m时,窃听者的位置随机变化.
3.2 神经网络性能验证
本文共为训练数据生成65万个样本(即L=650 000).为了选择神经网络模型的超参数,同时避免过拟合问题,这些训练数据的10%随机用于验证阶段.在ANN模型中,批量大小为1 024,为了确保模型的最佳性能,本文选择初始学习率为0.001.在获得训练好的ANN模型后,生成1万个新的样本作为测试数据来评价该模型的性能.
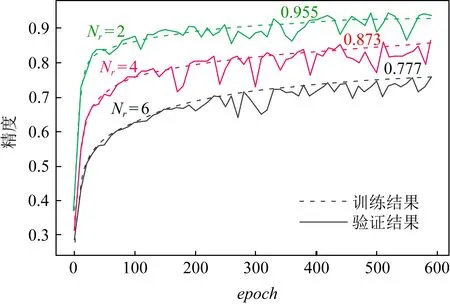
图3 不同中继节点数量的神经网络性能分析
图3示出对应于继电器数量的3个不同模型在训练和验证集上每个训练阶段的收敛情况.从图3可以看出,训练数据集和验证数据集的精度随着epoch的增大都在稳步提高.每个模型的训练线和验证线之间的差距是最小的,这意味着不存在过拟合问题.此外,神经网络方法的性能与继电器的数量或输入大小成反比.可见,基于双中继器系统和具有6个中继器系统的神经网络模型的准确率分别为95.5%和77.7%.
3.3 中继数量对无线网信息安全性能的影响分析
图4示出窃听者在dEx=120 m和dEx=160 m位置上的保密率随中继器数量变化的过程.此外,该图还给出了不同Nr值下的穷举搜索方法和神经网络机器学习方法的对比.基于神经网络的系统和基于穷举搜索的系统其保密率都随着中继器数量Nr的增加而增加.这说明在给定S-D距离条件下,通过增加跳数可以提高系统的保密性能.当Nr<4时,而ANN方法的结果接近于穷举搜索方法.
3.4 窃听位置对无线网信息安全性能的影响分析
图5给出了ANN方法和支撑向量机(support vector machine, SVM)方法的性能比较,以及用不同Nr值穷举搜索窃听者位置变化的结果.显然,窃听者的位置对机器学习方法的性能有直接影响.当窃听者位于源附近(dEx<100 m)时,机器学习方法的有效性显著,当窃听者位于源较远(dEx>100 m)时,SVM方法的性能相对较低.在大部分情况下,神经网络方法的有效性都高于SVM方法.此外,当网络变得更加复杂、中继数量更多时,SVM方法的性能明显下降,而ANN方法的结果接近于穷举搜索方法.

图5 神经网络方法与支持向量机方法的性能比较
3.5 中继数量和窃听位置对信息安全性的影响分析
CT方案、最佳中继选择方案、DT方案这3种传动方案的比较如图6所示.图6(a)(b)分别采用2个中继器和6个中继器作为通信链路模型.2张图的结果中都具有1个共同点,即本文的ANN方案的保密性优于CT方案、最佳中继选择方案和DT方案.不同之处在于,随着中继器数量的增加,4种方案的整体保密性都有所提高.这说明,在实际应用中,适当增加中继数量可提高整个通信链路的保密性.
4 结 语
本文通过人工神经网络的方法选择出能够克服具有“DF中继限制”的无线网络中的最优保密率问题.仿真结果表明,本文方法与穷举搜索方法相比,在显著缩短计算时间的同时,能使系统的保密率达到最优;增加跳数可以提高系统的安全性;本文所提出的中继选择方案的保密性能优于2跳传输方案和DT方案.该结构具有可重构性,能够通过实际无线信道数据重新训练模型来适配特定的应用场景,而无需从头构建新的模型.本文方案可以应用于具有多个窃听者的大规模网络,能有效解决在多跳中继无线通信过程的保密率问题.

