一种基于自注意力机制的深度学习侧信道攻击方法
周梓馨 张功萱 寇小勇 杨 威
(南京理工大学计算机科学与工程学院 南京 210094)
随着信息技术的发展,嵌入式设备的数量日益增长,其安全性越来越受到重视,侧信道攻击是主要威胁之一[1].侧信道攻击的核心思想是利用密码芯片运行过程中泄露的物理信息获取密钥信息(如功耗、电磁辐射等).根据对目标设备的访问和控制级别,侧信道分析可以分为2类:建模攻击(如模板攻击[2])和非建模攻击(如差分能量攻击[3]).侧信道建模攻击假设攻击者拥有与目标设备相同类型的设备,并对其拥有充分的访问控制权限,攻击者通过对相同类型设备充分学习后将拥有对该设备的刻画能力,并尝试将这种刻画应用到目标设备进行攻击.机器学习的方法可以很容易地将非线性处理用于侧信道攻击[4-8]:Masure等人[9]通过信息论的研究证明了神经网络在侧信道攻击中的效果;Valk等人[10]通过引入猜测熵偏差方差分解,进一步提高了神经网络在侧信道攻击中的可解释性.
随着深度学习的兴起,侧信道攻击研究者在监督学习下使用深度神经网络构建攻击模型进行侧信道攻击[11-13]:Maghrebi等人[11]证明了基于深度学习的侧信道攻击可以有效地攻击未采用掩码保护的AES算法实现.Timon[14]首次实现了在非监督学习下使用深度学习进行非建模攻击,攻击密钥的一个字节时,针对密钥空间的每一个猜测密钥建立1个模型进行攻击.Maghrebi等人和Cagli等人[11-12]通过构建卷积神经网络攻击模型成功地过滤了AES实现的失调对策;Carbone等人[13]成功地攻击了采用失调对策的公钥实现:多层感知机同样可以很好地攻击采取失调对策的加密措施[12,15].Perin等人[1]通过集成学习将多个简单模型进行集成来达到强模型的攻击效果,为深度学习侧信道攻击领域提供了一种新思路.Maghrebi[16]提出一种新的基于多标签分类的方法,使得模型从8 b密钥块到更大的密钥块(16 b)的攻击而不引入额外的开销.Picek等人[17]深入研究了机器学习侧信道攻击中存在数据不平衡的优点与缺点,并使用各种数据平衡方法提高攻击效果,攻击所需能量迹数量减少7/8.Cagli等人[12]提出一种基于CNN的端到端的分析方法,在能量迹存在偏差的情况下可以简化评估过程.Lu等人[18]提出一种基于注意力机制[19-23]端到端的处理原始能量迹的方法,构建了一个基于编码器架构的模型,但该模型的循环层不能并行化,训练时将耗费大量时间.Kwon等人[24]使用降噪标签,通过真实数据中的噪声训练自编码器,训练好的自编码器可以用于预处理,降低输入数据中的噪声.Prouff等人[25]提出了特定数据集的超参数选择方法,但仅仅局限于特定的数据集.Zaid等人[26]提出了一种构建高效CNN架构的方法,依据可视化技术(如热图、梯度可视化、权重可视化)的结果选择超参数.Rijsdijk[27]使用强化学习寻找最佳超参数,但该方法目前仅适用于可训练超参数比较少的情况.
目前基于深度学习的侧信道攻击攻击成功仍然需要大量能量迹,模型效率有待进一步提升;模型在训练时存在快速过拟合[12,14,25,28]以及深度学习所具有的梯度消失、收敛速度慢等问题.通过使用数据增强[12]、添加噪声到输入能量迹[15]中、随机移位[25,28]等方法可以缓解过拟合问题,但无法从根本上解决该问题.Vaswani等人[29]在2017年首次提出自注意力机制,并基于自注意力机制提出了可以并发训练的新模型Transformer,使用全局视角对特征分配注意力,解决了卷积神经网络的局部特征提取能力不足的问题,同时结合丢弃层和残差网络,解决了传统神经网络在模型训练时存在的快速过拟合和梯度消失问题.然而,Transformer结构并不适用于侧信道攻击,因为其采用了多层编码器解码器架构用于解决NLP领域中文本前后的关联性,而在侧信道攻击中,能量迹之间没有时序关系.侧信道攻击模型属于建模阶段建立的一个分类模型,与攻击阶段独立.本文借鉴了Transformer架构中的编码器设计,将自注意力机制引入侧信道攻击中并提出一个基于自注意力机制的深度学习侧信道攻击模型SADLSCA,通过开展实验验证了SADLSCA的高效性.本文的主要贡献有3个方面:
1) 引入自注意力机制用于侧信道攻击,使深度学习侧信道攻击有新的特征提取方式,并在公开数据集ASCAD(1)ASCAD数据集获取地址为https://github.com/ANSSI-FR/ASCAD和CHES CTF 2018(2)CHES CTF 2018数据集获取地址为https://chesctf.riscure.com/2018news上通过实验验证了自注意力机制在侧信道攻击中有良好的特征提取效果;
2) 基于自注意力机制构建一个深度学习侧信道攻击模型SADLSCA,解决了快速过拟合、梯度消失、收敛速度慢等问题,并在公开数据集上表现出良好的攻击效果,验证了SADLSCA在侧信道攻击时的可用性和高效性;
3) 通过对单层编码器结构的模型进行实验测试,给出了单层编码器结构的模型达到最佳性能效果的常用超参数数值.
1 相关技术
1.1 符号定义
用T表示能量迹集合,T=(t1,t2,…,tN);N表示集合中能量迹的数量;P表示明文或密文集合;K表示密钥集合;Y表示与P和K相关的中间值变量,分别由pi,j,ki,j,yi,j组成,其中i表示能量迹的取值范围,j表示字节的索引.
1.2 深度学习侧信道攻击
深度学习侧信道攻击本质上属于建模攻击,模型由深度学习构建.在构建攻击密钥的第j个字节的模型时,使用一个大小为N的训练集,ti,f为训练集中的第i条能量迹的第f个特征值,与ti对应的中间值为yi,j=f(pi,j,ki,j).本文使用的泄露函数为
yi,j=Sbox(pi,j⊕ki,j),
(1)
其中,⊕为异或运算,Sbox对应S盒,是AES算法的字节替换运算.
在建模阶段,使用泄露函数计算每条能量迹的中间值作为其标签.随机将数据pi和密钥ki输入到受控设备后,采集该设备泄露的物理信息得到能量迹.训练完成后,从受控设备采集1个验证集数据用于验证模型的泛化能力.在攻击阶段,从拥有未知密钥k*的待攻击设备上收集攻击集数据,将攻击集数据输入模型得到输出.根据模型的输出计算可能性最大的猜测密钥概率pk,并认为它是真正的密钥k*.其理论依据为贝叶斯公式与极大似然相关:
pk=P[k|T]=
(2)
其中,pk表示使用Na条能量迹攻击的情况下,根据模型的输出计算每个猜测密钥的概率.在Na越小、正确密钥k*对应的概率pk*越大的情况下,模型效果越好.
1.3 评价指标
Picek等人[17]提出精确率、召回率等常见的机器学习指标与成功率、猜测熵等常见的侧信道攻击指标之间存在不一致性,即机器学习常用指标并不适合作为侧信道攻击模型的评估指标.Standaert等人[30]指出侧信道攻击中的标准度量是成功率和猜测熵.Zhang等人[31]在数据不平衡的条件下使用交叉熵比指标比交叉熵指标更适用于评估侧信道攻击中深度学习模型的性能.Masure等人[9]证明了在深度学习侧信道攻击模型中选择最小负对数似然损失函数(NLL)是有效的.Zaid等人[32]提出了排名损失函数,与交叉熵损失函数相比,估计误差减少23%.在模型的训练阶段,由于排名损失函数会耗费极大的计算资源而得不偿失,所以只要所选的损失函数可以保证模型在训练过程中使得输入所对应的输出分类标签的概率最大即可,最终选择的损失函数为交叉熵损失函数:
(3)
其中,n为能量迹的个数,q(ti)为模型对第i条能量迹预测的概率分布,p(ti)为第i条能量迹的真实概率分布.在验证和攻击阶段,使用成功率和猜测熵揭示正确的密钥.攻击阶段中,给定Na条能量迹,以概率递减的顺序输出猜测向量:g=(g1,g2,…,g|K|),其中,|K|为密钥空间大小.成功率定义为g1等于真实密钥k*的平均经验概率;猜测熵定义为k*在猜测向量g中的平均位置.
1.4 自注意力机制
在侧信道攻击领域中, Lu等人[23]首次提出了一种基于注意力机制的端到端处理原始能量迹的方法.Vaswani等人[29]首次提出自注意力机制,并基于自注意力机制提出一种新的简单的网络结构Trasnformer,完全基于注意力机制,不需要任何卷积操作,具有更高的并行化能力,减少了训练时间.2021年,Dosovitskiy等人[33]提出的模型Vision Transformer是基于Vaswani提出的自注意力机制构建的一种高效图片分类模型.Vaswani和Dosovitskiy等人提出的自注意力机制和模型适用于图像分类,不能用于侧信道攻击领域,本文对其作了优化使其适用于侧信道攻击.
注意力函数是将1个查询Query(Q)和1个键值对集合(K,V)映射到1个输出Output的函数(此处的K与上文的密钥集合不同),其中Q,K,V和Output都是向量.输出Output是由值的加权和计算得出,分配给每个值的权重由Q与相应的K计算出的矩阵决定.具体结构如图1(a)所示:

图1 自注意力机制
对于能量迹集合T中的第i条能量迹ti,j,其有n个特征点,即j=1,2,…,n,为了简洁表示,此处记ti,j为Xj,计算注意力的过程如图1(b)所示.输入的能量迹、变换后的Q,K,V以及输出Output都是长度为n的向量.输出Output是加权后得到的,重要的特征将会得到更大的值.本文使用的是缩放点积自注意力,公式为
(4)
其中,n为一条能量迹的特征数量,Dropout以概率p丢弃输入的每一个特征,丢弃层可以对模型正则化,避免模型快速过拟合.文献[29]证明了缩放点积自注意力机制将使模型更快地收敛并且空间效率更高.
与文献[29]不同的是,能量迹输入是一维数据.不考虑能量迹之间的关联性,因为能量迹之间的关联性体现在攻击阶段,建立模板阶段只考虑分类问题,这是侧信道模板攻击和NLP的显著区别.因此,放弃了多头注意力和掩蔽多头注意力机制以适应对1维能量迹分配注意力的场景.具体地,Input是1条维度为1×n的能量迹,Q,K,V由输入的能量迹经过LayerNormal对其n个点进行正则化后分别进入3个全连接网络学习得到,其中LayerNormal归一化可以加速网络收敛速度.然后Q和K进行矩阵点积运算进入匹配操作,紧接着Softmax层用于归一化不同特征所分配到的注意力大小.Dropout可以对其正则化,这使得训练出的网络模型泛化能力更强.然后将最终注意力与V进行矩阵点积运算,将不重要的特征点赋予极小的权值,从而屏蔽能量迹中不重要的点集,赋予大的权值给重要的特征来提取出对模型分类重要的兴趣点,完成特征提取操作.
2 SADLSCA模型结构
本节将详细介绍SADLSCA模型.首先用实验验证自注意力机制在侧信道攻击领域是有效的.对输入的能量迹进行1层全连接分类,如图2所示,猜测熵没有收敛到0.然后在输入和含有256个神经元的全连接层之间放入图1的注意力机制模块,再次训练模型,猜测熵可以收敛到0,至此验证了自注意力模块可以提取特征.
Transformer结构采用了多层编码器解码器架构用于解决NLP领域中文本前后的关联性,而在侧信道攻击中,能量迹之间没有时序关系.因此庞大的Transformer架构并不适用于侧信道攻击.本文采纳了Transformer和Vision Transformer编码器部分的优点,构建了轻量级的适用于侧信道攻击的模型SADLSCA,如图3所示.模型分为3部分:输入数据处理、编码器、分类头.

图2 单层神经网络

图3 SADLSCA模型结构
2.1 输入数据处理
输入数据处理由BatchNormal[34],Positional Encoding[29]和Dropout[35]这3个模块组成.BatchNormal用于对输入数据进行归一化,加速模型的训练速度,使得模型更快地收敛.Positional Encoding用于对输入数据进行位置编码.Vaswani等人[29]指出自注意力机制的运算方式会丢失特征的时序关系,所以需要对能量迹的位置信息进行编码,编码后的每条能量迹特征之间的时序关系被唯一确定.位置编码使得能量迹的每个特征都是独一无二的,避免了打乱特征位置放入模型却得到相同的输出.在1条能量迹中,尤其是采用了防护措施的数据集上,能量迹中的特征点的位置关系极其重要,因为和能量泄露的时间点相关联.Vaswani提出相应的位置编码公式,由于能量迹的特征是1维数字,无法直接使用Vaswani提供的公式,所以选择了文献[33]中Dosovitskiy提出的位置编码思想,直接对输入的能量迹加上相同维度的可训练参数即可.Dropout是丢弃层,以概率p丢弃输入的每个特征,丢弃层可以对模型正则化,避免模型快速过拟合.
2.2 编码器
编码器是模型最核心的部分,主要有Self-Attention和MLP Block 2部分.编码器的设计使得输入与输出保持相同的形状,因此可以叠加多层编码器以适应大数据集的训练,使得模型效果更佳.编码器总体结构采用2层残差结构便于梯度反向传播,使得梯度有效回传,加快模型收敛的速度,解决了梯度消失和模型收敛速度慢的问题.对于编码器的输入X和输出Y满足如下公式:
Z=X+W0(fDropout(SATTN(X)))+b0,
(5)
Y=Z+MB(LNORM(Z)),
(6)
MB(X)=fDropout(W2(fDropout(fGELU(W1Z+
b1)))+b2),
(7)
其中:SATTN函数为图1对应的式(4),用于计算注意力W0,W1,W2为全连接网络的矩阵;b0,b2,b2为其对应的偏置参数;MB(X)为MLP Block所对应的网络;fDropout为丢弃层网络.
在编码器中,LayerNormal用于标准化每条能量迹的特征,加速模型的收敛速度.能量迹进入3个不同的全连接网络得到3个相同形状的向量Q,K,V,用于求自注意力.此处的LayerNormal,Q,K,V和自注意力模块与图1的结构完全相同,拆分出来仅仅是为了方便观察残差结构,该模块可以并行化训练,减少模型的训练时间.编码器中的线性层和丢弃层与输入保持相同的形状,其中丢弃层用于正则化以避免模型在训练过程中快速过拟合的状况.
编码器中多层感知机块(MLP Block)的设计借鉴了文献[33]的结构和经验,一共2层全连接,第1层全连接网络的神经元个数是输入特征个数的4倍;第2层全连接网络的神经元个数与多层感知机输入的特征数量相同,GELU激活函数避免了模型在输入数值比较小的情况下梯度消失的问题,文献[25]证明了在建模阶段GELU激活函数会表现得更好.2个Dropout层对模型正则化,避免模型快速过拟合.
2.3 多层感知机分类头(MLP Head)
MLP Head由3层全连接网络和2层RELU激活函数层组成:第1层全连接网络的神经元个数是输入数据特征的一半;第2层全连接网络用于分类,其神经元个数由泄露函数决定,取值9或256.第1层全连接网络神经元个数减半是为了剔除一半不重要的特征,将重要的特征压缩,从而提取出比较重要的特征.同理,第2层网络在第1层网络的基础上再次减少一半的特征数量,最终使用第2层全连接网络进行进一步分类达到更佳效果,这种神经网络设计借鉴了卷积网络中全连接网络展开层的设计.RELU使模型在输入数值大于0 的情况下梯度可以快速地反向传播,模型会更加关注对正确分类起到决定性作用的特征.模型在训练过程中不需要Softmax层,直接使用Pytorch集成的交叉熵损失函数可以获得更好的数值稳定性.在攻击阶段需要先使用Softmax层输出各个类别的所占权重的比例.
值得注意的是,当编码器只有1个时SADLSCA属于简单模型,可以在小数据集上训练出很好的效果.当数据集增大时,为了使得模型效果更好,有2个方法:第一,增加编码器的个数,虽然模型中使用多个编码器会训练更长时间,编码器并行化训练加速模型收敛速度.同时,Vaswani等人[29]指出当数据集比较大时,编码器的叠加效果将更好.第二,由于SADLSCA在编码器个数为1的情况下仍然属于简单模型,并且可以收敛,Perin等人[1]证明了集成方法在机器学习侧信道攻击领域内仍然有效,SADLSCA单层编码器模型是属于简单模型,可以使用集成的方法.
3 实验验证
3.1 实验环境
实验环境为Python3.8+Pytorch1.8.1+cuda10.1;服务器内存为128 GB,显卡为GM206GL;显存为4 GB.
3.2 数据集介绍
使用的数据集为ASCAD和CHES CTF 2018,是采集电磁辐射的能量迹组成的数据集.本文的分析同样可以扩展到其他侧信道攻击泄露数据集,如能耗泄露.
1) ASCAD数据集.
ASCAD数据集[25]是由Prouff发布的,由屏蔽AES-128在8位微控制器(ATmega8515)上软件实现时被采集的测量值组成,算法实现采用了布尔掩蔽对策和随机延迟对策.在第1轮加密中,与密钥关联的第1个字节和第2个字节未受到掩码保护,即前2个字节的掩码为0,其余14个密钥字节掩码都是随机的.其中有2个数据集版本,第1版本数据集拥有5万条能量迹用于训练神经网络,1万条能量迹用于攻击,且它们的密钥是固定的,每条能量迹包含700个时间样本点(特征).注意,这1万条能量迹拆分成2份,各5 000条分别用于验证和攻击,记为ASCAD_fixed_key.第2版本数据集包含20万条能量迹用于训练神经网络且密钥可变,10万条能量轨迹用于攻击且密钥固定,每条能量迹包含1 400个时间样本点(特征).同样将这1万条能量迹拆分成2份用于验证和攻击,记为ASCAD_variable_key.
2) CHES CTF 2018数据集.
该数据集是2018年密码硬件和嵌入式系统会议(the Conference on Cryptographic Hardware and Embedded Systems, CHES)发布的.该数据集由屏蔽AES-128运行在32位STM微控制器上的测量值组成.算法实现采用布尔掩蔽对策且16位掩码随机生成.训练集包含4.5万条能量迹且密钥固定,验证集和攻击集各含2 500条能量迹且密钥固定,攻击集和验证集密钥相同但与训练集的密钥不同.每条能量迹由2 200个时间样本(特征)组成,记为CHES_CTF_2018.
3.3 模型初始化设置
SADLSCA中网络的权重分布初始化为均值为0、标准差为1的正态分布,位置编码可学习参数初始化为0.
3.4 超参数选择
在模型训练时选择了一些超参数,本文参考已有的参数选择建议[1,25,29-30],以下的超参数取值是穷举了参数部分取值得出的较好选择.一些超参数的选择如表1所示.
超参数的介绍和选择理由如下:
1)batch_size设置为512,即每批次读取512条能量迹放入模型进行训练.
2)epochs用于控制模型训练的次数.
3)learining_rate的设置一共3种:0.000 05,0.000 01和0.000 005.
4)leakage_model有很多可选项,模型在ASCAD数据集上训练时设置为具有256个密钥空间的中间值模型.在CHES_CTF_2018上训练模型时,设置为汉明重量模型.
5)num_class数值由泄露模型决定,所以这个超参数设置为256和9(对应汉明重量模型).
6)target_byte是被攻击密钥的字节索引(从0开始),在攻击ASCAD数据集时设置为2,即攻击密钥的第3个字节.在攻击CHES_CTF_2018数据集时设置为0.
7)target_dataset有3个可选项,分别为ASCAD_v1_fixed_key, ASCAD_v1_variable_key, CHES_CTF_2018,用于加载不同数据集的参数信息.
8)dropout用于控制丢弃层丢弃神经元的概率,可以单独为每个丢弃层设置不同的概率,避免快速过拟合的状况.
9)num_features与数据集能量迹的特征数量保持一致.
10)depth用于设置编码器的个数以适用于不同大小的数据集.
11)kr_step用于控制在攻击阶段中求取key rank的步长,可以使得攻击效果稳定,采取Perin的实现源码的数值[1],设置为10.
12)runs用于设置混洗次数,设置为100.在攻击阶段求猜测熵时会对模型的输出混洗多次进行攻击,然后取其平均值作为最终攻击结果.
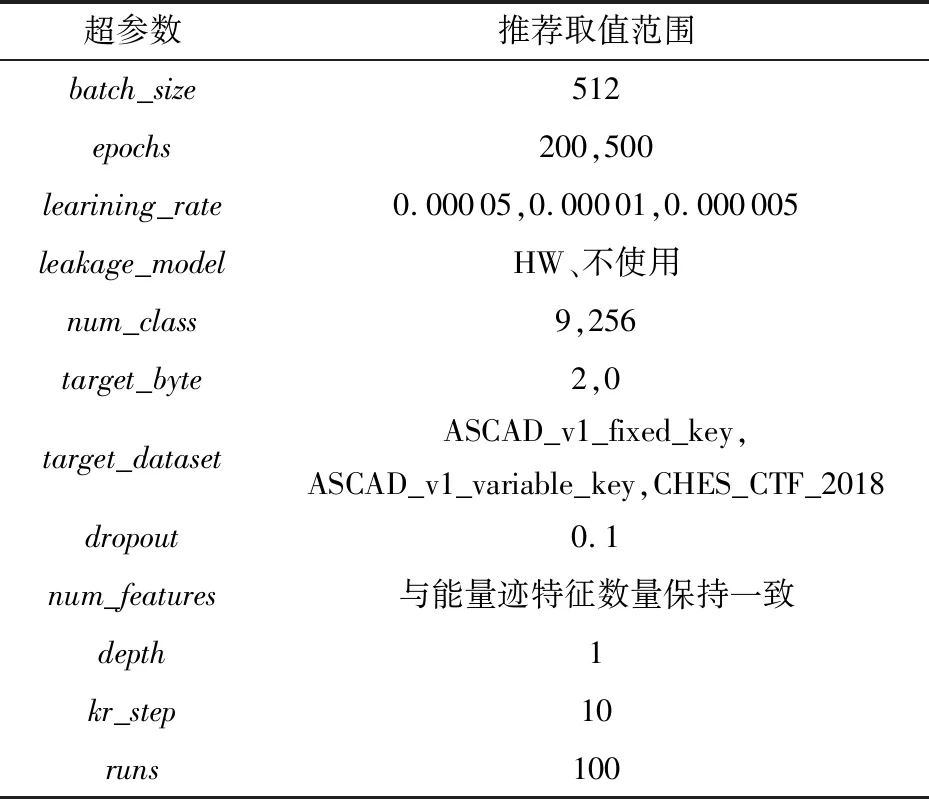
表1 超参数的选择
3.5 模型效果分析
本节主要通过实验证明SADLSCA对解决快速过拟合、梯度消失和收敛速度慢等问题的效果,实验在数据集ASCAD_fixed_key上进行验证,实验参数与3.6节的ASCAD_fixed_key实验中的设置相同,默认为3.4节中推荐的参数选择.

图4 dropout的不同取值对depth不同模型攻击时的正则化效果
ASCAD_fixed_key是1个小数据集,在训练的过程中最容易发生快速过拟合的状况,本文在该数据集上通过实验探究SADLSCA中的dropout层是否能解决机器学习侧信道攻击领域中快速过拟合的问题.随着网络层数的加深,模型在训练过程中梯度反向传播会出现减弱甚至消失的情况,SADLSCA收敛速度会变慢,针对该数据集使网络模型采用不同depth值进行实验,并分析SADLSCA是否能解决梯度消失和收敛速度慢的问题.其中dropout设置为0~0.9,步长为0.1;depth设置为1~6,步长为1;其余超参数与3.6节的ASCAD_fixed_key实验中设置相同,保持固定.
图4示出depth为1~6,dropout分别为0.1,0.3,0.5,0.7和0.9,迭代1~600次时模型攻击成功所需要的能量迹数量.当depth=1时,为了对比效果,将dropout=0时的结果也进行了绘图,即图5(a)中depth=1的蓝色曲线,可以很明显观察到,其和dropout=0.1时相似,很快可以达到最佳攻击效果,SADLSCA仅仅需要迭代100次便可以使用25条能量迹攻击成功,并且比dropout=0.1时收敛更快,但也很快出现过拟合的状况,随着迭代次数的增加,其攻击成功所需要的能量迹数量逐渐增加.然而dropout为0.5,0.7和0.9时就相对平缓很多,没有出现过拟合的状况,但随着dropout的增大,模型的收敛速度会变慢,这是预料之中的,因为丢弃的概率越大,模型拟合的效果就被削弱得更大,在减少过拟合的同时也减少了模型正常拟合的效果.
随着depth增加,过拟合状况会增强,以dropout为0.1为例,当depth增加到3,4,5时,SADLSCA在迭代600次时想要攻击成功需要100条左右能量迹数量,过拟合极其严重,这也反向说明了编码器块数的增加(即模型深度增加)会加速模型拟合效果,网络收敛所需要的迭代次数也明显减少(depth为1时需要100次迭代,depth为5时仅仅需要50次左右),这也侧面验证了SADLSCA纵向扩展(增加网络深度)是有效的.同时也验证了SADLSCA在网络层数加深的情况下不会出现梯度消失和收敛速度慢的问题,这个效果来源于残差网络结构.
depth增加的同时,增加dropout同样可以抑制过拟合,直观地看,在该数据集上dropout为0.5和0.7时较好,SADLSCA整体表现得较为平缓.若继续增加dropout,模型收敛速度太慢,反而丢失了性能,花费太多时间训练模型得不偿失,比如在depth为6,dropout为0.9时,图5中甚至没有紫色的曲线,这是因为模型在训练600次依旧没有收敛到很好的攻击效果,其攻击成功所需能量迹超过200条,所以不在图中显示,事实上其攻击成功所需要的能量迹已经超过500条.
虽然模型攻击效果的评价指标是猜测熵,但模型在训练时采用的交叉熵损失函数,两者虽然不是绝对的同步关系,但相关性依然很大,否则也不会在模型训练阶段采用交叉熵损失函数.为了验证droput取值对模型最终猜测熵的影响是否与模型训练时损失值有关,给出了模型depth分别为1,3和5以及各个dropout数值对模型训练时在验证集上的损失指标变化情况,如图6所示:

图5 dropout的不同取值对depth不同模型训练时的正则化效果
图5说明了当dropout增加时会缓解快速过拟合的状况,不考虑图中dropout为0.9的情况(因为由图4和之前的分析,这种情况下模型没有很好地收敛),即使在depth增加的情况下,dropout的增加依然可以很好地缓解过拟合,这也验证了dropout可以缓解模型训练时的过拟合状况.
3.6 实验结果与分析
本文通过公开的数据集验证了SADLSCA用于侧信道攻击是有效的,这3个数据集为ASCAD_fixed_key,ASCAD_variable_key,CHES_CTF_2018.如无特别说明,超参数默认为3.4节中给出的数值.
1) ASCAD_fixed_key.
训练集包含5万条能量迹,验证集和攻击集合各500条能量迹用于验证和攻击,且密钥都是固定且相同的,每条能量迹包含700个时间样本点.设置学习率learining_rate为0.000 01,epochs为200,depth为1,target_byte为2(第3个字节),runs为100,图6展示了SADLSCA(黄色和绿色)以及现有的方法模型在训练迭代次数为134和216情况下150条能量迹对该数据集进行攻击的猜测熵(图6(a))和成功率(图6(b))的具体变化情况;图6(a)中红色曲线所对应的模型是由文献[25]针对ASCAD数据集提供的开源的并训练好的最佳CNN模型,模型迭代训练75次,由6层CNN网络组成,每层200个神经元个数,batch_size=200,num_class=256;图6(a)中蓝色曲线对应的Ensemble模型是由文献[1]提供的开源集成学习模型,且集成的是MLP模型,使用汉明重量泄露模型,num_class为9,按照其最佳参数设置模型,一共50个模型,每个模型迭代50次,每个模型的模型超级参数由给定范围的数值区间中取得.
图6(a)示出SADLSCA在迭代134和216次情况下的猜测熵变化,SADLSCA猜测熵很快就降到0(为了直观地通过结果对比得出结论,对猜测熵取对数并绘图),比最佳CNN模型和集成学习模型效果更好.图6(a)中红色曲线的震荡展示了最佳CNN模型攻击效果的不稳定性,这种不稳定性一方面来自CNN只能提取局部空间信息的特性,而SADLSCA以全局视角提取特征信息;另一方面来源其runs为1,求得的是单次结果,中间出现震荡意味着并没有真正收敛,而SADLSCA和集成模型的结果runs为100,求的是平均值,而且自注意机制擅长以全局视角提取特征,因此SADLSCA的数值曲线更加稳定平滑.蓝色曲线表示的集成学习虽然比较稳定,但其收敛速度显然没有SADLSCA快,甚至在使用了150条能量迹攻击下猜测熵没有收敛到0,其最终在数值350时收敛,这是因为集成学习模型的效果比较稳定.图6(b)展示了SADLSCA的成功率,数值大约在25可以攻击成功,与最佳CNN模型需要数值在55附近才能稳定相比,减少了54.5%的能量迹数量,SADLSCA更加稳定,整体曲线平滑;与集成学习模型需要数值在350附近才能收敛的结果相比,减少了91%的能量迹数量,SADLSCA攻击效果更好.同时注意到,迭代次数为134和216的攻击结果却相近,这是由于模型中Dropout模块起到了正则化的作用,避免了模型快速拟合.

图6 学习率为0.000 01、epochs为134和216的猜测熵和成功率
2) ASCAD_variable_key.
训练集包含20万条能量迹且密钥随机,验证集和攻击集各5 000条能量迹用于验证和攻击并且密钥固定,每条能量迹包含1 400个时间样本点,该数据集合比较大.
设置学习率learining_rate为0.000 01,epochs为200,target_byte为2(第3个字节),runs为100,图7(a)展示了SADLSCA(黄色和绿色)以及现有的方法模型训练迭代次数为67和78情况下150条能量迹对该数据集进行攻击的猜测熵(图7(a))和成功率(图7(b))的具体变化情况.其中红色曲线所对应的模型是最佳CNN模型[25],蓝色曲线所对应的Ensemble曲线是集成学习模型[1].

图7 学习率为0.000 01、epochs为67和78的猜测熵和成功率
图7(a)的结果展示了SADLSCA在迭代67和78次情况下猜测熵的变化,图7(a)中黄色和绿色曲线是SADLSCA分别在迭代67,78次下的攻击结果,最终收敛于数值50左右.图7(a)中红色曲线的震荡原因与3.4节ASCAD_fixed_key中的原因相同,最佳CNN模型最终收敛于数值70左右.同时蓝色曲线表示的集成学习收敛速度显然没有SADLSCA快,其最终在数值65左右收敛.图7(b)同样清晰展示了SADLSCA的成功率,绿色曲线是SADLSCA迭代78时的攻击成功率,数值大约在50~60之间可以攻击成功,与最佳CNN模型需要数值在70附近才能稳定相比,减少了28.6%的能量迹数量,SADLSCA更加稳定,整体曲线平滑;与集成学习模型需要数值在65附近才能收敛的结果相比,减少了23.1%的能量迹数量,同样彰显了SADLSCA的高效性.

图8 epochs为10,13,15,17,18的猜测熵和成功率
3) CHES _CTF_2018.
因为该数据集已经进行过预处理,所以模型中的BatchNormal对于该数据集而言是多余的模块.训练集包含4.5万条能量迹且密钥固定,验证集和攻击集各250条能量迹用于验证和攻击,密钥固定且与训练集密钥不同,每条能量迹包含2 200个时间样本点.设置学习率learining_rate为0.000 05,epochs为100,depth为1,target_byte为0(第1个字节),runs为100,dropout为0.1和0.2,leakage_model为HW(汉明重量模型),图8展示了模型以及使用集成学习模型在训练次数分别为10,13,15,17,18的情况下进行攻击求得的猜测熵(图8(a))和成功率(图8(b))的具体变化情况,图8(a)中蓝色曲线对应的Ensemble模型是由文献[1]提供的开源集成学习模型,其余曲线都是SADLSCA在不同迭代次数下的攻击效果,具体见图例.
图8(a)展示了集成MLP网络的方式在处理CHES_CT_2018数据集时不能收敛,与文献[1]结论相同,这是由于该数据集生成的过程中使用了随机掩码,而MLP网络空间平移不变性较差,导致MLP模型攻击效果较差.图8(b)展示了SADLSCA在数值大约为175时可以攻击成功,此时成功率为1.与文献[1]中使用集成学习对50个CNN模型分别训练50次进行集成的方法需要300条能量迹攻击才能收敛相比,攻击所需能量迹数量减少了41.7%,同时SADLSCA是单层编码器且仅需10~20次训练就达到这个攻击效果,收敛速度很快并且攻击效果更好.
4 总结和未来的工作
本文主要的研究工作是在深度学习侧信道攻击中引入了自注意力机制,对自注意力机制作了详细介绍并使其适用于深度学习侧信道攻击.基于自注意力机制构建了一个深度学习侧信道攻击模型SADLSCA,解决了基于深度学习的侧信道攻击模型在训练时存在的快速过拟合、梯度消失和收敛速度慢等问题,并在ASCAD_v1_fixed_key,ASCAD_v1_variable_key,CHES_CTF_2018这3个公开数据集上进行实验,实验结果验证了SADLSCA的可用性和高效性,同时本文给出了SADLSCA可以达到很好攻击效果的常用超参数数值.
攻击阶段中,猜测熵的计算所耗费的内存空间与攻击集中能量迹的数量成正比,计算猜测熵会极大地消耗存储资源和计算资源.Transformer架构[29]的输出是状态的叠加,攻击过程中猜测熵的求解也是状态的叠加,两者有着天然的关联.因此,下一步我们将主要研究使用Transformer解码器架构构建模型取代模板攻击中的攻击阶段,避免攻击阶段中猜测熵的计算,提升攻击效率.

