基于背景噪声经验格林函数的地震准确定位精度分析——以2008年甘肃武都地震为例

王烁帆， 倪四道*， 王伟涛， 曾祥方， 谢军， 韩宏博

1 中国科学院精密测量科学与技术创新研究院， 大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学 地球与行星科学学院， 北京 100049 3 中国地震局地球物理研究所， 北京 100081 4 中国科学技术大学 地球与空间科学学院， 合肥 230026

0 引言

地震定位是地震学研究的基本问题之一.准确的震源位置具有重要意义，例如，它能够为抗震减灾工作提供关键信息，它奠定了研究地球内部速度结构的重要基础.常规的地震定位方法使用一维速度结构模型，通过拟合多个台站P波、S波的到时反演震源位置.为了得到准确的位置，该方法需要满足震中附近有近台，台站方位角覆盖良好，以及使用可靠的速度结构模型等条件(Bondár et al., 2004；王未来等，2014；Wang et al., 2018; 易桂喜等, 2019).但是，一些地震发生在台网稀疏且三维速度结构复杂的地区，近年来国内外学者发展了一种基于背景噪声经验格林函数进行路径校正的地震定位方法，为稀疏台网情形下地震准确定位研究提供了新思路(Zhan et al., 2011; Barmin et al., 2011; Xie et al., 2011, 2020; Levshin et al., 2012; Zeng et al., 2015).

通过两个地震台站长时间的背景噪声波形记录进行互相关，可以得到包含两个台站之间真实速度结构信息的经验格林函数，该思路已被成熟地应用于内部结构成像研究中(Shapiro and Campillo, 2004; Yao et al., 2006; 齐诚等, 2007; Lin et al., 2008; 王伟涛等, 2011; 鲁来玉等, 2014; 徐义贤和罗银河, 2015; Xie et al., 2021).近年来，国内外学者将背景噪声经验格林函数(empirical Green′s functions，EGFs)用于地震重定位研究，利用包含地下速度结构信息的噪声EGFs，对地震波进行路径校正，有效地压制路径上速度结构异常引起的误差，进而提高地震定位精度(图1).其中Barmin等(2011)将震源区附近密集流动台网与远台的噪声EGFs，进行插值叠加合成震源附近网格点的理论地震图，再通过拟合波形包络搜索震源位置.同年Zhan等(2011)提出基于稀疏台网的定位方法，即利用震源区附近参考台与远台的噪声EGFs和理论格林函数的时移，对地震波形拟合的时移量进行校正，得到地震位置.然而影响波形偏移的因素，除了速度结构差异，还有震源机制解的偏差.理论研究表明，两个台站之间的噪声EGFs可以近似为单力源激发产生的波形，而大多数情况下地震波形则由双力偶源激发产生.二者震源机制解不同，会在波形拟合过程中造成一些时间上的偏差，从而引起一部分定位误差.

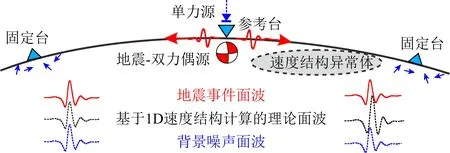
图1 基于背景噪声经验格林函数(EGFs)地震定位方法示意图蓝色实心箭头表示远处噪声源，正三角形表示固定台，倒三角形表示流动台(参考台).双力偶表示地震的震源模型，而虚线箭头表示虚拟事件的单力源.灰色区域表示速度异常体.红色实线波形表示地震面波，黑色波形表示基于区域1D速度结构计算的理论面波波形，而蓝色波形表示噪声EGFs.Fig.1 Schematic diagram of the relocation method based on ambient noise empirical Green′s function (EGFs)The blue solid arrows represent the distant noise sources. The regular triangles represent the permanent stations, and the inverted triangle represents the portable station (reference station). The beach ball represents the earthquake source, and the dashed arrow represents the single force source of the virtual event. The gray area represents the velocity anomaly region. The red solid waveforms represent the seismic surface waveforms. The black waveforms represent the theoretical waveforms calculated based on the regional 1D velocity model, and the blue waveforms represent the noise EGFs.

震源机制解对于面波群速度影响小(Levshin et al., 1999), 而且观测数据显示地震波形和噪声EGFs的频散曲线有较好一致性(Bao et al., 2014).Xie等(2011)以1998年中国北部张北MW5.7地震为例，比较了基于波形偏移(Zhan et al., 2011)和走时校正两种方法的定位结果精度，发现依据走时校正的定位结果偏差小于基于波形偏移定位结果偏差.Zeng等(2015)通过理论测试发现在不同的震源机制解情况下，基于噪声EGFs面波群走时定位方法能够得到稳定和准确的震源位置.在2017年格陵兰岛的滑坡事件定位研究中，使用噪声EGFs面波群走时方法得到的定位结果与卫星遥感影像观测的位置相差2.5 km，明显优于传统方法得到的结果(偏差10 km以上)，再次验证了该方法的可靠性(Xie et al., 2020).

基于背景噪声经验格林函数面波群走时的定位方法，为稀疏台网中的地震准确定位研究提供了新思路.由于参考台的绝对位置已知，理论上这种方法在稀疏台网情况下，也可以得到高精度的震中位置结果.关于该方法精度分析，已有的研究限于所用台站较少，对于参考台震中距、震源区附近速度结构不均匀性以及远台分布稀疏程度等因素还缺少系统测试.本文选择了中国西部一个已经准确测定位置的中等浅源地震作为研究案例，分析基于噪声EGFs定位结果精度的影响因素，并讨论该方法的稳定性和适用情况.

1 方法原理

基于该方法进行地震定位主要步骤如下：首先使用震中附近的流动台作为参考台，将参考台与远处固定台的垂向连续波形记录进行互相关并叠加得到EGFs；之后测量噪声EGFs和地震波形中的Rayleigh面波群走时；然后利用噪声EGFs面波群走时对地震波形进行路径校正.根据误差函数公式(1)，在震中区附近网格搜索最佳震中位置(Xie et al., 2011, 2020).为了减少搜索时间，我们先根据最小二乘算法公式(2)估计发震时间的偏差t0，再代入公式(1)中搜索得到震中位置.公式(1)—(2)中，d为网格点(可能的震源位置)与固定台的震中距，u和v分别为某个台站地震波形记录和噪声EGFs中某个周期的Rayleigh面波群速度，D为参考台与固定台的台间距.

(1)

(2)

2 震例选择

2008年武都MS5.5地震发生在甘肃、四川、陕西三省交界地区，地质构造单元属于青藏高原和四川盆地交界，三维结构变化剧烈，可用于测试噪声EGFs地震定位方法精度.此外本文选取该地震作为案例分析，还进一步考虑了三个方面的因素：(1)武都地震的震中位置已经准确测定.InSAR观测到武都地震所引起的明显地表形变，能够确定准确的震中位置，这为我们评估地震定位结果精度提供了关键基础(Weston et al., 2011).Luo等(2019)将震前2008年7月16日和震后2009年7月19日两景ALOS SAR影像数据进行处理，经过相位解缠，得到沿卫星视向线地表形变场(如图2c).在北纬32.98°，东经105.57°附近区域约2 km×2 km范围内有明显的形变，最大达7 cm.我们将这一位置作为2008年武都地震的震中位置，并为接下来的定位结果精度测试提供标准值(表1).(2)该地震的震级合适.根据地震标度律估算(Wells and Coppersmith, 1994)，该地震震源破裂尺度约为3 km，其矩心震中和起始震中相差小于1.5 km，该地震可以视为点源，有利于对定位结果的精度进行分析.此外，此次地震能量强，远台能够清晰地记录到这次地震事件的波形.(3)数据充足.除了国家地震台网提供的固定台地震波形数据，震中附近在2009—2012年期间布设了5个流动台(参考台)，其中S426位于震中西北方向相距62 km，S522位于震中东部相距49 km，S615位于震中北部相距26 km，S616位于震中西部相距8 km，S617位于震中西南方向相距23 km.接下来，本文将这5个流动台分别作为参考台，对武都地震震中进行重定位.

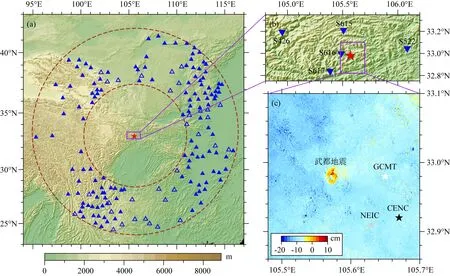
图2 2008年武都地震位置和台站分布图(a) 震中距500～1000 km范围内固定台的分布情况，实心三角形表示定位使用的台站，空心三角形表示未使用的台站.红色五角星表示2008年武都地震的InSAR震中位置； (b) 5个流动台(参考台站)的空间分布位置； (c) 2008年武都地震InSAR观测的沿视线向地表形变场，和中国地震台网中心(CENC)，美国国家地震信息中心(NEIC)以及美国哥伦比亚大学的Global CMT(GCMT)地震目录提供的武都地震震中位置.Fig.2 The 2008 Wudu earthquake and distribution of the seismic stations(a) The permanent stations with the epicentral distance in the range of 500～1000 km. Solid triangles represent the stations used in this study, and hollow triangles represent the unused stations. The red star represents the 2008 Wudu earthquake. (b) The distribution of five portable stations (reference stations). (c) Line-of-sight surface deformation field observed by InSAR during the 2008 Wudu earthquake, and the epicenter locations from different catalogs, including the China Seismic Network Center (CENC), the US National Earthquake Information Center (NEIC), and the Global CMT (GCMT).

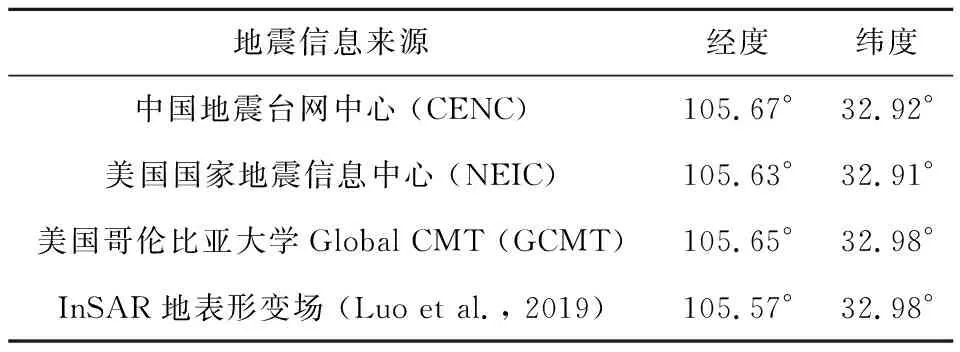
表1 不同目录提供的2008年武都地震震中位置Table 1 The epicenter locations of the 2008 Wudu earthquake from different catalogs

3 数据处理

计算参考台和固定台之间的背景噪声格林函数时，本文选取了国家地震台网震中距500～1000 km范围内169个固定台.台站间距大于5倍的面波波长，满足经验格林函数中面波可近似为行波的条件(Zhan and Ni, 2010).接下来对固定台和参考台2009—2012年期间的连续波形记录进行预处理，将垂向连续波形记录以天为单位进行截取，以1 Hz的频率进行重采样，去除均值和线性趋势，去除仪器响应得到表示质点运动速度的波形.我们将波形数据按照每段时长7200 s，重叠时长3600 s的格式截取.为了压制连续波形记录中地震事件信号和固定噪声源信号，我们采用滑动平均方法进行时间域的归一化，然后进行谱白化处理(Bensen et al., 2007).

完成以上数据预处理的操作步骤后，分别计算了震源区附近5个参考台S426、S522、S615、S616、S617和远处169个固定台之间垂向-垂向分量(ZZ)的互相关函数.波形信噪比以叠加时长的根号倍增加(Bensen et al., 2007)，为了保证信噪比最佳，对所有台站将连续1～2年的全部记录进行叠加，作为背景噪声经验格林函数EGFs，其物理含义为假设参考台作为虚拟单力源，固定台所接收到的波形.但实际噪声源空间分布不均匀，会导致噪声EGFs正负支振幅不同(Lin et al., 2008).Bao等(2014)比较了地震波形、噪声EGFs振幅强的半支波形以及噪声EGFs正负支叠加后波形的频散曲线，3种频散曲线趋势一致，其中噪声EGFs正负支波形叠加后提取的频散与地震波形频散的形态和趋势更为接近.于是，本文取噪声EGFs正负两支相加的对称波形作为研究对象.另外，将地震波形数据进行去均值、去趋势，去除仪器响应的预处理，并对垂向分量数据进行降采样得到频率为1 Hz的波形数据，接下来测量地震波形数据和噪声EGFs中Rayleigh面波的频散曲线(图3).

图3 地震波形(a)与参考台和固定台的噪声EGFs(b—f)Fig.3 Seismic waveforms (a) and the noise EGFs between reference stations and permanent stations (b—f)

提取频散曲线有多种方法(如, Levshin et al., 1992; Herrmann, 2013)，例如多重滤波法(Computer Program in Seismology, CPS330中的do_mft方法)和时频分析法(Frequency-Time Analysis, FTAN).本研究以S616与固定台之间的背景噪声格林函数为例，使用3种不同的方法，多重滤波法do_mft、时频分析法FTAN、以及将波形使用相位匹配滤波技术校正后再用时频分析法FTAN分别提取频散曲线.经过比较发现3种方法得到的频散曲线基本相似，考虑到为了方便对频散曲线进行质量控制，本研究使用人工交互界面的do_mft方法测量频散.参照CPS的使用软件说明(Herrmann, 2013)，对不同震中距的台站选取不同滤波器宽度α，对于震中距500～750 km的台站，α=25；震中距750～1000 km，α=50.

本研究主要提取了地震波形和噪声EGFs 能量集中的共同波段10～30 s面波频散数据(图4).为了定量化描述地震波形和噪声EGFs频散曲线的相似性，本研究根据公式(3)计算了10～30 s周期内两条面波频散曲线差异的均方根E.该公式描述了某段周期内地震事件波形和噪声EGFs频散曲线的差值均方根.其中，Veq和VEGFs分别表示所测量的地震波形和噪声EGFs中某一周期Rayleigh面波的速度.n为频散曲线在计算波段内的周期个数，周期间隔为1 s.差异度的单位为km·s-1，数值越小，则意味着地震波形和噪声EGFs的频散曲线越相似.

(3)

4 重定位结果与分析

本文分别以5个流动台作为参考台，使用背景噪声EGFs和地震波形10～30 s波段的频散数据进行地震重定位.删除了一些地震事件波形记录有问题的台站，使用135个数据良好的固定台进行了对比分析.统计了噪声EGFs和事件波形的频散数据，大部分频散曲线差异度在0.2 km·s-1以内(图5)，这说明同一固定台所记录的地震波形和噪声EGFs的频散数据普遍比较接近.台站方位角覆盖较好，除了方位角150°～180°区域，其他方位上每30°均有数据约束.我们以CENC目录提供的震中位置(105.67°，32.92°)作为初始位置，并在震中附近1°范围内，进行步长间隔为0.01°的网格搜索，得到五组地震重定位结果(表2).基于参考台S426的定位结果位于震源区北部，与InSAR观测最大形变区域相距3 km；基于参考台S522的定位结果位于震中东侧2 km处；基于参考台S615、S616、S617定位结果，均分布在地表形变增加的区域，与最大形变区域偏差在1 km左右(如图6a).

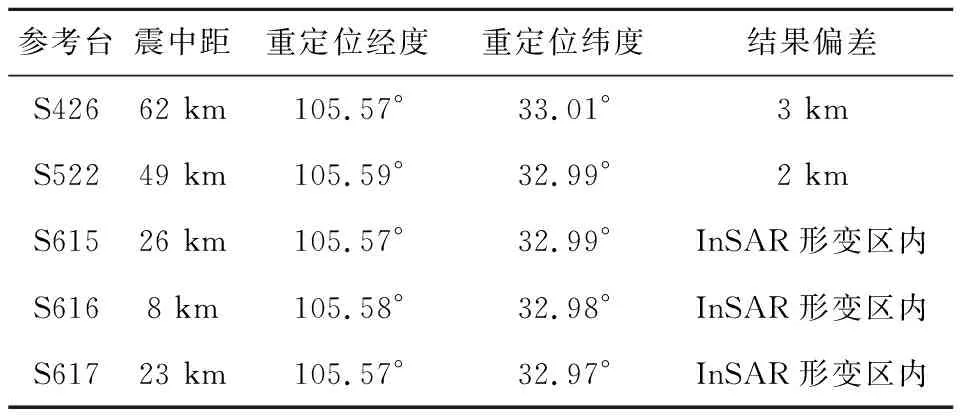
表2 基于5个不同参考台2008年武都地震重定位结果Table 2 The relocation results of 2008 Wudu earthquake based on the five reference stations

考虑到频散曲线测量过程中可能存在人为误差，我们使用统计方法中的卡方分布以及误差椭圆的方法对重定位结果进行误差分析.假设已有n个观测量，反演模型m所包含的3个随机变量即发震时刻和震中经纬度位置，满足高斯分布且独立同分布，那么模型m满足自由度ndf=n-3的卡方分布2.我们通过网格搜索得到最小误差点作为模型的最优解mbest，计算所有观测走时和基于mbest计算的理论到时之间的方差，作为偏差统计量σ2(公式(4)).通过查表得到80%置信区间的卡方阈值(http:∥www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html)，计算得到其对应的误差范围(公式(5)). 以上五组重定位实验中的80%置信区间的误差椭圆(如图6b)长轴为北西-南东方向约5～8 km；短轴为北东-南西方向约3～5 km.这可能是由于方位角150°～180°区域缺少数据覆盖，定位结果在北西-南东方向存在相对较大不准确性.

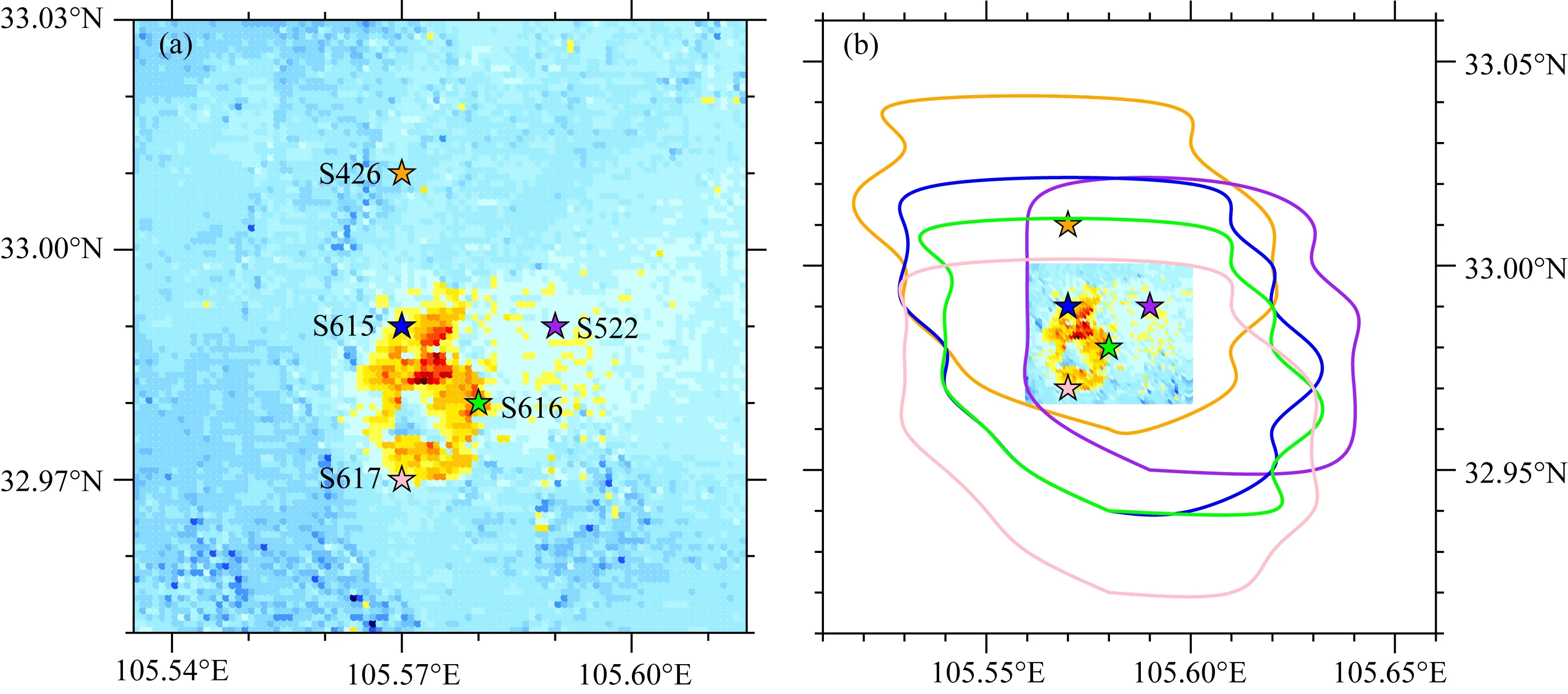
图6 地震重定位结果及统计误差(a) 分别以S426、S522、S615、S616、S617作为参考台进行地震重定位的结果，不同参考台对应图中橙色五角星、紫色五角星、蓝色五角星、绿色五角星，粉色五角星. (b) 中用相同颜色的曲线描绘了五组定位测试中的80%置信区间.Fig.6 The relocation results of the earthquake and the statistical error(a) The relocation results (star) by different reference stations S426 (orange), S522 (purple), S615 (blue), S616 (green) and S617 (pink). (b) The corresponding 80% confidence ellipses for results in (a).

(4)

(5)

5 讨论

与InSAR观测的武都地震位置相比，CENC目录定位结果向东南方向偏11 km，NEIC目录向东南方向偏9 km，而Global CMT目录向东偏7 km.从震源物理意义而言，利用中长周期波形拟合方法的Global CMT目录得到矩心震中的位置，而利用震相走时定位的CENC和NEIC目录得到起始震中位置.但根据地震标度律，五级地震破裂通常为3 km，起始震中和矩心震中相对距离不超过1.5 km.因此，此次地震Global CMT位置和CENC位置或者NEIC位置之间的差异，显著超过了起始震中和矩心震中的相对距离.不同地震目录对于武都地震定位误差的原因主要有两个方面：(1)三维速度结构的复杂性.(2)震中附近缺少近台约束.距离震中最近的固定台是四川省青川台(QCH)，位于武都地震的西南方向，震中距大于50 km，这导致使用国家地震固定台网定位的CENC目录结果有较大的不准确性.而对比本文的结果，基于噪声EGFs面波群走时路径校正的方法可以有效地压制传播路径上速度异常体带来的影响，在地震发生缺少近台的情况下，根据震中附近其他时间架设的参考台得到高精度的地震矩心震中位置.

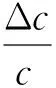
(6)

S616的定位结果如图7所示，其中基于S426的定位结果位于S616真实位置的北侧偏约3 km，利用S522和S615定位结果位于S616真实位置的北侧偏约1 km，而利用S617定位结果位于S616真实位置西南侧偏约1 km.可知武都地震震中30 km以内速度结构造成的定位偏差约1 km，震中60 km速度结构造成的定位偏差约3 km.可以看出基于武都地震重定位结果和S616虚拟震源的重定位结果位置空间分布基本接近，由此推测武都地震重定位结果偏差主要是由于震中区速度结构变化造成的，震源项对于定位结果影响较小.这也说明随着参考台震中距的增加，震源区速度结构差异带来的定位结果不准确度也会增加.

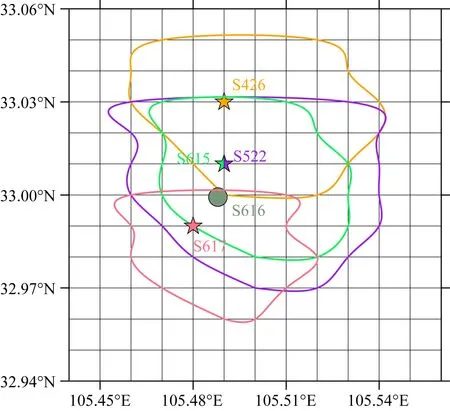
图7 震中附近区域速度结构对定位结果影响圆点表示S616的真实位置，五角星表示基于不同参考台S426(橙色)，S522(紫色)，S615(绿色)和S617(粉色)得到的S616重定位位置.图中用对应颜色的曲线描绘了80%置信区间.Fig.7 The influence of velocity structure near the source area on the relocation results The dot represents the true location of S616, and the stars represent the relocation of S616 based on stations S426 (orange), S522 (purple), S615 (green) and S617 (pink). The curves represent corresponding 80% confidence ellipses.

本研究进一步分析了使用不同频段进行定位以及噪声叠加时长对于定位精度的影响.单独使用10～20 s、20～30 s频段进行定位测试，定位结果偏差在5 km以内，但普遍比使用10～30 s得到的定位结果偏差大.所以在定位过程中使用频段尽可能的宽可以增加射线覆盖，能够有效提高地震定位精度.另外，互相关叠加时长是能否提取可靠噪声EGFs的关键，一般来说叠加时长越长，信噪比越好，定位结果可靠.而在实际定位研究过程中连续噪声记录时长有限，那么利用不同时长的噪声对应事件定位精度如何呢？本研究进行了以下测试，当叠加时长为1年的时候，可以消除季节性变化的背景噪声信号影响，得到稳定、可靠的定位结果.使用震中距30 km参考台站，得到定位结果偏差2 km以内，震中距50～60 km参考台的定位结果偏差3 km以内.而当叠加时长为半年180天的测试结果，显示使用震中距30 km以内台站定位结果偏差3～5 km.而使用震中距50～60 km参考台的偏差在3 km以内，推测这可能是由于震源区和台站之间明显的速度结构差异，与季节性变化噪声信号共同作用影响.使用震中距30 km以内参考台，当叠加时长为1季度时，定位结果偏差在3 km以内，当噪声叠加时长1个月，一般也可以得到定位精度在5 km以内的结果.

为了进一步测试该方法在台网特别稀疏环境下的适用性，本研究在震中距500～1000 km范围内取10个左右的固定台站重新测定震中位置.先按照方位角每60°一个间隔，将频散曲线差异度0.1 km·s-1以内和0.05 km·s-1以内的固定台按照方位角60°一个间隔，划分在6个分区域内.接下来在每个分区域内随机抽取1～2个台站的频散数据，一次重采样的样本容量为6～12个固定台，本研究分别以5个流动台为参考台站，进行了1000次重定位.

结果显示当噪声EGFs与地震波形频散曲线相似程度高时，重定位结果集中在InSAR震中附近.基于震中距8 km的S616参考台，使用6～12个震中距500～1000 km台站，当使用的频散数据差异度小于0.1 km·s-1，有80%的重定位结果在震中5 km以内，45%的结果在3 km以内(图8).当使用差异度小于0.05 km·s-1的频散数据时，99%的重定位结果分布在震中5 km范围内，78%的结果在震中3 km以内(图9).基于不同震中距参考台重定位测试结果显示，利用较少固定台，且方位角覆盖不全的情况下，参考台震中距越近，定位结果越可靠.随着参考台震中距增加，震源区不同方位的结构差异，以及远台方位角分布等因素会耦合影响定位精度(表3).

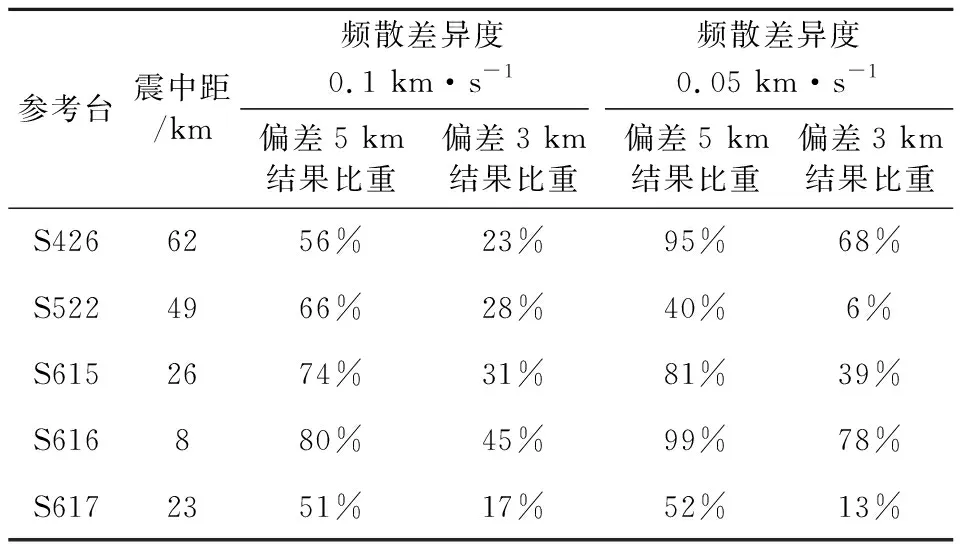
表3 利用不同差异度频散数据重定位测试结果Table 3 The relocation results were obtained using the dispersion data with diverse root mean square differences

图8 基于稀疏台网利用频散曲线差异度0.1 km·s-1的重定位测试(a) 频散曲线差异度随方位角分布； (b) 1000次测试中抽样台站个数； (c) 重采样定位结果分布.底图为InSAR观测的沿视线向地表形变量，方框的大小表示该位置在结果中出现的频次，方框越大，出现的频次越高.紫色圈表示震中(InSAR最大形变点) 5 km范围内，橙色圈表示震中3 km范围内.Fig.8 The relocation test with the dispersion curve difference of 0.1 km·s-1 for sparse network(a) The azimuthal distribution of the dispersion curve difference; (b) The number of resampled stations at 1000 tests; (c) The results of 1000 relocation tests. The base map shows the line-of-sight (LOS) surface deformation observed by InSAR. The box size represents the number of relocation results appearing in the same grid, with the box more significant, the number bigger. The purple circle indicates the epicenter (the maximum deformation of InSAR) region within 5 km, and the orange circle indicates the epicenter within 3 km.

图9 基于稀疏台网利用频散曲线差异度0.05 km·s-1的重定位测试(详情见图8)Fig.9 The relocation test with the dispersion difference of 0.05 km·s-1 for sparse network (See also Fig.8 for details)

本研究继续测试了台网更加稀疏的情况，分别以S426、S522、S615、S616、S617作为参考台，利用4个方位角分布均匀的固定台进行重定位.这4个固定台分别是位于北侧的NM.BYT，东侧的HA.ZMD，南侧的YN.MAL以及西侧的QH.YUS(图10).利用互相关函数叠加时间超过1年数据，提取10～30 s频段噪声EGFs面波频散数据，且与地震面波频散差异度小于0.1 km·s-1，相对定位的结果显示当参考台在震中距30 km以内，定位精度小于3 km.

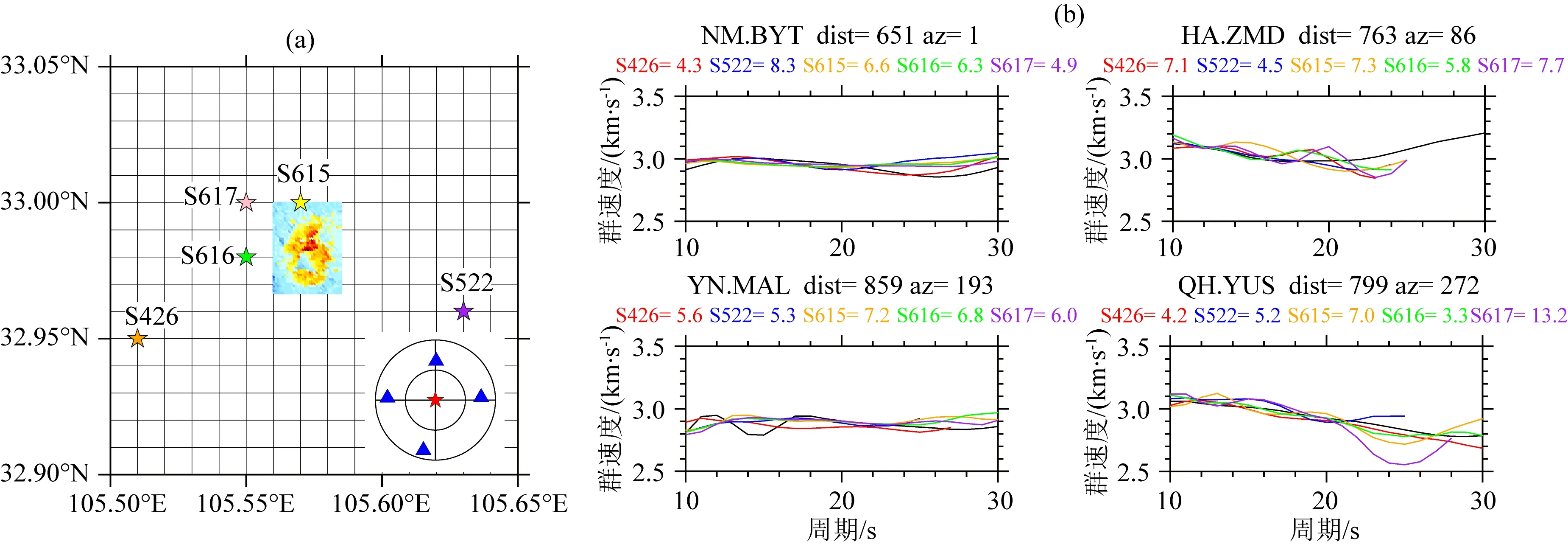
图10 利用不同参考台基于4个固定台地震重定位测试(a) 重定位结果； (b) 本次实验所用噪声和地震波形的频散曲线对比. Fig.10 The relocation test with different reference stations used by 4 permanent stations(a) The relocation results; (b) The dispersion curve of the noise EGFs and seismic waveforms used in this test.

目前在很多地区，台站较为密集，三维结构也有比较可靠的模型，传统的P、S波到时定位方法效果应该很好.本文测试的方法可以适应于3种情况：(1)历史地震重定位研究.可以在历史地震发生的大致位置附近架设流动台站，对比EGFs与历史地震图；但是这有可能受到历史台站时钟偏差的影响，需要进一步发展历史地震台站时钟准确度估计方法.(2)近期发生在稀疏台网地区的地震重定位研究.例如发生在非洲大陆或澳大利亚大陆内部的地震，还有发生在海域的地震，如1996年长江口海域地震等，可以通过事后架设流动台或海底地震仪(Ocean Bottom Seismograph, OBS).而对于大洋海岸附近的地震，噪声EGFs与地震图可能存在较大差异，且地震台方位分布不理想，定位误差可能较大，这还需要进一步的案例分析研究.(3)未来地震快速准确定位研究.在地震危险性高的断层附近，架设流动台站观测，建立背景噪声格林函数库，以期能够对未来发生的地震进行快速、准确的定位.

6 结论

本文基于背景噪声格林函数面波群走时校正的地震重定位方法，通过2008年武都地震重定位震例研究发现，利用震中距30 km以内的参考台，重定位结果与InSAR震中位置偏差在1 km以内，震中距超过30 km的参考台得到重定位结果偏差约3 km.这些误差主要源于武都震中区速度结构变化，随着使用参考台震中距的增加，震源区速度结构差异带来的定位结果不准确度也会增加.之后本文进一步测试了噪声叠加时长，波形频段，以及稀疏台网等因素.结果显示使用震中距30 km以内参考台，使用较宽频段频散数据，在噪声叠加时长1个月的情况下，也可以得到误差在5 km以内的定位结果，当噪声叠加时长超过1年，定位结果更稳定可靠，位置偏差可缩小到1 km以内.稀疏台网测试结果显示使用10个左右固定台进行重定位，在频散数据良好的情况下，定位结果精度可达3 km.

本文对基于背景噪声格林函数准确震中位置测定方法的参数组合方案进行了系统分析，给出了该方法的高精度地震定位所需的固定台网及参考台站的观测指标体系.然而本文只利用了噪声记录的垂向-垂向(ZZ)分量进行互相关提取Rayleigh面波，未来可以进一步尝试使用背景噪声径向-径向(RR)，垂向-径向(ZR或RZ)分量提取Rayleigh面波或者切向-切向(TT)分量互相关提取Love面波(Lin et al., 2008; Levshin et al., 2012; Hu et al., 2020)和地震波形对比，用于地震重定位研究.另外随着高性能计算和地球模型研究的进步，可以结合背景噪声格林函数和理论三维格林函数，并结合地震学、大地测量学、构造地质学等多种数据，进一步发展高精度地震震源参数测定方法.

致谢感谢编辑、编委与评审专家对完善本文提出的具有建设性的意见.本文InSAR观测处理结果由中国科学院精密测量科学与技术创新研究院沈强副研究员提供.中国地质大学(武汉)罗银河教授、南方科技大学杨英杰教授、中国地质大学(北京)李红谊教授、中国地震局地球物理研究所韩立波研究员对文章提出了宝贵意见，在此一并致以衷心感谢.