水力压裂有效压裂半径的影响因素研究*

贾进章，王东明，李 斌

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 阜新 123000；2.辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

0 引言

我国煤层渗透率小于1.0×10-3μm2的占70%以上，在高瓦斯和突出矿井中95%的开采煤层属于低渗透性煤层[1-2]。煤层透气性较差，瓦斯很难自然排出，进而导致井下煤层瓦斯含量大且压力高，给煤矿开采带来严重的安全问题。为高效抽采瓦斯，减少瓦斯事故，通常在抽采前使用增透技术提高煤层透气性。其中水力压裂技术相对安全可靠，还可对煤层起到润湿作用，故水力压裂逐渐成为前沿的增透技术[3]。

水力压裂有效压裂半径对增透效果的影响很大，如果能够准确地预测有效压裂半径，将极大地提高水力压裂的增透效果，为此，众多国内外科研人员对此进行了大量探索研究。Hubbert等[4]首次提出基于线弹性和非线性断裂力学的水力压裂理论，为以后对水力压裂有效压裂半径的模拟分析与实验探究奠定了基础；刘传义等[5]通过RFPA2D软件模拟了煤层的不同埋深和不同坚固系数对水力压裂有效压裂半径的影响，结论认为随着煤层埋深的增加，压裂半径随之减小，煤层坚固系数增加，压裂半径逐渐增大；Bouteca[6]首次将椭圆裂缝形变理论与二维流体流场结合起来，同时考虑了地应力不均匀变化,构造了一种全三维模型，并开展实验，结论认为水力压裂的扩展延伸方向是沿着椭圆进行裂隙延展；袁永榜等[7]基于压裂区与非压裂区对电磁波能量吸收有差距的原理提出了多频同步电磁波层析成像(CT)技术的煤层水力压裂范围探测方法，可较为精确地探测水力压裂的压裂范围；赵源等[8]对多种不同地应力条件下的水力压裂致裂过程进行模拟与分析，认为水力压裂增透范围大致可分为：宏观裂缝区、微裂隙贯通区、微裂隙产生区和原生裂隙扰动区；闫江平等[9]以水力压裂作业过程中煤体及其围岩的物性变化特征为研究基础，通过井下微震监测技术对某煤矿煤层水力压裂影响范围进行了探测，结论认为水力压裂的压裂范围受注水水压大小、煤层构造及煤体硬度的影响很大，注水压力与压裂范围呈正相关，增加煤层透气性及煤体硬度较小都不利于裂缝的产生和扩展。以上研究在一定程度上为水力压裂范围的确定提供了参考，并且推动了水力压裂增透技术的应用与发展，但由于影响压裂半径的因素较多，每个因素对压裂半径的影响程度不明确，导致对压裂半径的确定缺乏统一的标准。

鉴于此，本文拟在分析水力压裂有效半径影响因素的主次顺序上，理清各影响因素对压裂半径的影响程度，根据Mohr-Coulomb准则建立水力压裂渗流—损伤耦合方程并且求得水力压裂有效压裂半径计算公式。运用ABAQUS模拟软件，模拟地应力、注水水压、压裂孔径及弹性模量对水力压裂有效压裂半径的影响，再通过灰色关联分析法来确定多个影响因素中的主控因素，以期为水力压裂有效压裂半径的确定提供理论参考与借鉴。

1 水力压裂渗流—损伤耦合方程

在进行水力压裂增透作业过程中，高压水通过压裂孔流入煤层天然缝隙，由水压力产生并作用于煤层弱面的法向拉应力开始大于煤层的抗拉强度与地应力在该方向的分量之和时，煤体开始出现破裂损伤[10]，根据Mohr-Coulomb准则，损伤单元的弹性模量关系表达如式(1)所示：

E=(1-D)E0

(1)

式中：D为损伤变量；E为损伤单元的弹性模量，GPa；E0为无损单元的弹性模量，GPa。

煤层的剪切应力F达到Mohr-Coulomb损伤临界值，即式(2)时：

(2)

式中：σ1，σ3分别为最大主应力和最小主应力，MPa；φ为内摩擦角，(°)；fc为抗压强度，MPa。

损伤变量D表示为式(3)：

(3)

式中：ε为应变临界值；fcr为抗压残余强度，MPa；εc0为最大压应变；εr为残余应变。

对应单元的透气系数按式(4)表达：

(4)

式中：K0为透气系数，m2/(MPa2·d)；α瓦斯压力系数；β为应力影响系数；P为瓦斯压力，MPa；ξ为透气系数的增大系数，m2/(MPa2·d)。

当单元达到抗拉强度ft损伤阈值时，σ3可表示为式(5)：

σ3≤-ft

(5)

式中：ft为抗拉强度，MPa。

损伤变量D按式(6)表达：

(6)

式中：ftr为抗拉残余强度，MPa；εtu为极限拉应变；εt0为最大拉伸应变。

对应单元透气系数的描述按式(7)表述：

(7)

式中：λ为煤层损伤时透气系数，m2/(MPa2·d)；λ0为初始透气系数，m2/(MPa2·d)；ξ′为煤体破坏时透气系数的增大系数，m2/(MPa2·d)。

2 水力压裂破裂区半径分析

煤体进行水力压裂作业后形成破裂区、塑性区和弹性区[11]。煤体应力F应满足Mohr-Coulomb准则，如式(8)所示：

F=σθ-Nσr-S=0

(8)

式中：σθ，σr分别为极坐标的径向和环向应力值，N；N，S为材料参数。

破裂区应力应变方程如式(9)所示：

(9)

塑性区应力应变方程如式(10)所示：

(10)

式中：Cc为破裂区黏聚力，N；φc为破裂区摩擦角，(°)；Cp为塑性区黏聚力，N；φp为塑性区摩擦角，(°)。

煤层经过水力压裂后，压裂孔周围会出现裂缝，煤体损伤变形，模量显著减小，钻孔前后的变形模量比值为卸压系数K。通过卸压系数K的大小来分析卸压效果及煤层透气性。

根据巴布柯CO经验公式，卸压系数K如式(11)所示：

(11)

求得破碎区半径R如式(12)所示：

(12)

式中：W为压裂孔边界距离，mm；D2为压裂孔孔径，mm；S2为水力压裂后钻屑量与常规钻孔钻屑量比值；K2为松散系数；a为压裂孔半径，m。

3 水力压裂数值模拟

3.1 数值模型的建立

本文根据马堡煤矿15号煤层203工作面井下实际情况构建二维数值模型，模型尺寸为12 m×8 m。在模型中心布置孔径为113 mm的压裂孔，在压裂孔两侧布置2个孔径为113 mm的导向孔，导向孔距压裂孔1.5 m，数值模型如图1所示。运用ABAQUS软件模拟煤层水力压裂演化特征，以水力压裂后煤体损伤分布(损伤变量D≥0.2)作为有效压裂半径的评价指标[8,12]，定量分析压裂损伤区域。根据现场实际情况，固定模型左边界在x方向上的位移，同时固定下边界在y方向上的位移，并在右边界的x方向上施加14 MPa的压应力，在上边界的y方向上施加18 MPa的压应力，计算区域的网格尺寸为0.35 m，网格数量为18 000，从压裂孔以恒定的注入速度q=1.7×10-3m2/s注入压裂液体。具体参数见表1。

图1 水力压裂数值模型

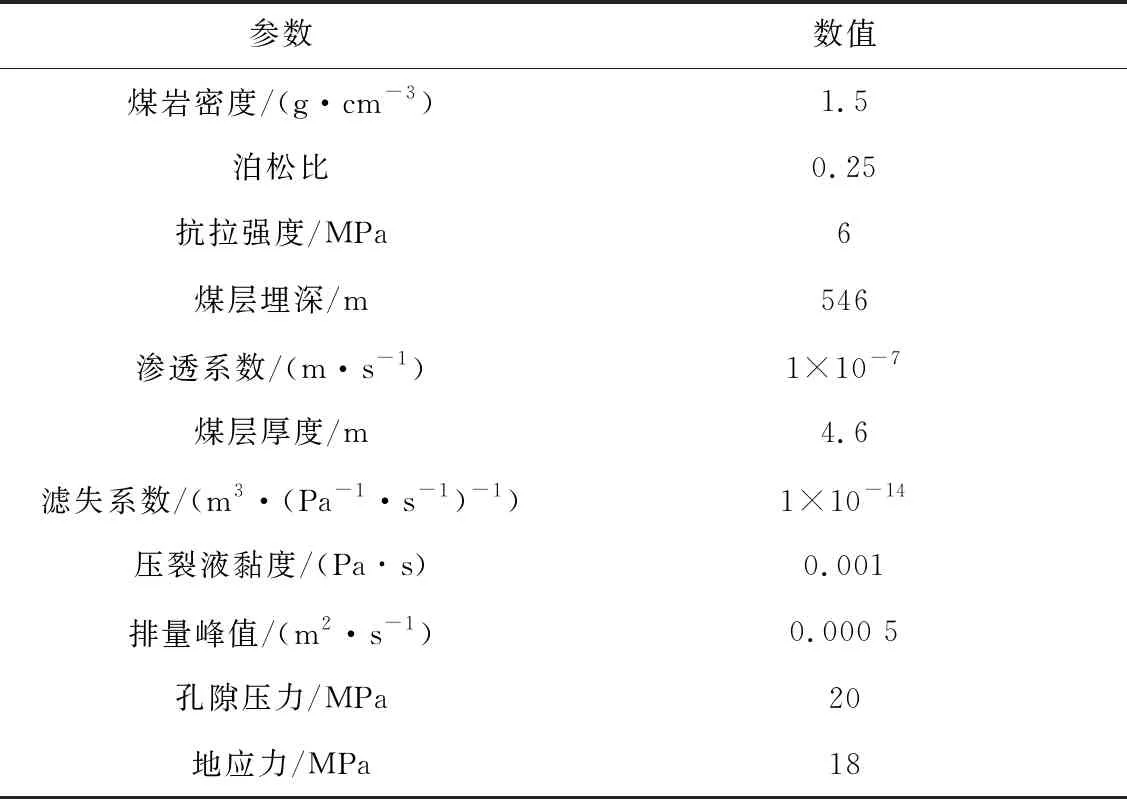
表1 数值模拟基础参数

3.2 数值模拟结果分析

为研究不同因素对煤层水力压裂效果的影响，根据矿井现场实际情况并结合文献[6,8,10,13]，选取各影响因素的参数取值见表2，利用ABAQUS软件进行分析。

表2 各因素的参数取值

3.2.1 地应力对压裂半径范围的影响分析

不同地应力下水力压裂有效压裂范围模拟如图2所示。此时注水压力为6 MPa，压裂孔径为72 mm，弹性模量为2.85 GPa，选取地应力分别为10，15，20，25 MPa，通过模拟软件测量得到有效压裂半径分别为4.82，4.25，3.68，3.11 m。

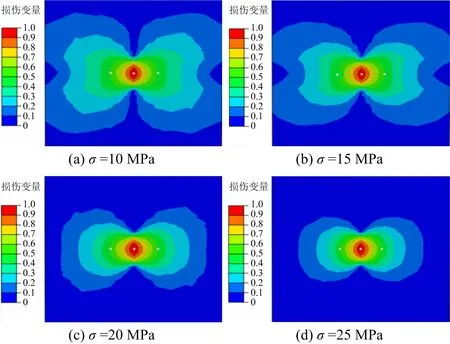
图2 不同地应力对水力压裂有效半径影响

由图2可以看出：随着地应力的增加，水力压裂有效压裂半径随之显著减小。因为煤体弱面破裂并形成宏观裂缝的条件是，由水压力形成的并作用于煤体弱面的法向拉应力超过煤体抗拉强度与地应力在该方向分量之和。但是随着开采深度增加，煤层地应力变大，地应力与煤体抗拉强度之和逐渐超过来自于水压力的法向拉应力，此时煤层不再破裂，压裂半径也就随之减小。所有对高地应力煤层在进行水力压裂增透作业时应该适当调整其他参数来弥补高地应力带来的负面影响。

3.2.2 注水压力对压裂半径范围的影响分析

地应力20 MPa，孔径94 mm，煤体弹性模量3.85 GPa，选取注水压力分别为6，8，10，12 MPa。不同注水压力下水力压裂煤层损伤范围变化模拟如图3所示，对应的有效压裂半径分别为2.66，3.08，3.50，3.92 m。

图3 不同注水压力对水力压裂有效半径影响

由图3可以看出：随着注水压力的增加，煤层压裂半径逐渐增加。因为在进行水力压裂过程中，水流入到裂隙之中，高压水克服裂隙阻力而运动[14]，注水压力越大，由注水压力产生并作用于煤层弱面的法向拉应力越大，法向拉应力就更容易大于煤体抗拉强度与地应力在该方向分量之和，煤体更易破裂，进而增加了压裂范围。因此，在井下进行水力压裂过程中，在保证安全作业的前提下，应该适当增加注水压力来提高水力压裂增透效果。

3.2.3 压裂孔径对压裂半径范围的影响分析

地应力15 MPa，注水压力8 MPa，弹性模量4.85 GPa，选取压裂孔径分别为72，94，113，133 mm。不同压裂孔径下水力压裂煤体损伤范围变化如图4所示，所对应的压裂半径分别为3.01，3.23，3.45，3.67 m。

图4 不同压裂孔径对水力压裂有效半径影响

由图4可知，随着压裂孔径的扩大，煤体损伤范围也小幅度增加，因为压裂孔孔径增加，能降低裂缝起裂压力[15]，并且增加裂缝长度。同时压裂孔孔径越大，对煤体结构破坏就越大，煤体结构就越容易失稳，出现贯通裂缝。而且孔径增大，压裂液的流量更大，从而使液体压入速度远远大于煤体自身的吸收速度，裂缝起裂更容易，进而增加压裂半径。故在现场进行水力压裂作业时，在经济允许的前提下，适当增加压裂孔径可以提高水力压裂增透效率。

3.2.4 弹性模量对压裂半径范围的影响分析

地应力25 MPa，注水压力10 MPa，压裂孔径133 mm，选取弹性模量分别为2.85，3.85，4.85，5.85 GPa。不同弹性模量下水力压裂煤体损伤范围变化如图5所示，此时对应的有效压裂半径分别为3.95，4.12，4.29，4.46 m。

图5 不同弹性模量对水力压裂有效半径影响

由图5可以看出：随着煤层弹性模量的增加，水力压裂有效压裂半径相应增大。因为弹性模量较高的煤体，其刚度大、塑性强，就容易出现塑性碎裂[16]。高弹性模量的煤体在进行水力压裂作业之后的主裂缝狭长、微裂隙发育充分、缝网面积大，故其增透范围更广，有效压裂半径更大。所以在选择增透方式时，弹性模量较高的煤层更适合运用水力压裂增透技术来增加煤层透气性。

4 水力压裂压裂半径影响因素分析

为确定地应力、注水压力、压裂孔径、弹性模量这4个因素对水力压裂有效压裂半径影响程度的强弱关系，运用灰色关联理论来确定这4个影响因素与有效压裂半径之间的关联度的主次顺序。

把水力压裂有效压裂半径作为母因素，子因素分别为地应力、注水压力、压裂孔径及弹性模量。不同影响因素的取值见表3。

表3 灰色绝对关联度数据

灰色关联度理论分析步骤[17]如下：

4.1 绝对关联度ε0i

绝对关联度ε0i计算如式(13)所示：

(13)

式中：s0为参照数列的始点零化像的有向面积；si为对比数列的始点零化像的有向面积。

根据文中的参考数据，令|si|，|s0|，|si-s0|如式(14)～(16)所示：

(14)

(15)

(16)

(17)

式中：xi(k)为第i个因素关于第k个对象的观测数据。

将式(14)～(17)代入式(13)，可求得各因素对有效压裂半径的绝对关联度。

4.2 灰色相对关联度γ0i

灰色相对关联度γ0i计算如式(18)所示：

(18)

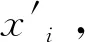
(19)

令：

(20)

4.3 灰色综合关联度δ

灰色综合关联度涵盖灰色绝对(相对)关联度的共同的优势，既可以对比数据之间的相关性又可以比较相对于数据始点变化趋势，计算方法如式(21)所示：

δ=ρε0i+(1-ρ)γ0i

(21)

式中：ρ为分配系数，取值为0.5。

综合关联度δ计算结果见表4。由表4可知，煤层地应力对水力压裂有效压裂半径的影响最大，综合关联度为0.785 3，其次是注水压力(δ=0.724 1)和压裂孔径(δ=0.692 8)，最后是弹性模量(δ=0.659 7)。

表4 综合关联度δ计算结果

因此，在煤矿井下进行水力压裂增透作业时，应该测试本煤层地应力数值，如果煤层地应力较大，在保证安全和经济允许的前提下可适当增加注水压力和压裂孔径，来使增透效果达到最佳。

5 结论

1)通过不同因素影响下煤体损伤范围模拟分析得到有效压裂半径与煤层地应力呈递减关系、与注水压力、压裂孔径及弹性模量呈递增关系。

2)通过灰色关联分析法求得4个影响因素对水力压裂有效压裂半径的影响程度排序为：煤层地应力>注水压力>压裂孔径>弹性模量。

3)在井下煤层进行水力压裂增透作业时，应该基于可靠的煤层地应力和弹性模量参数对注水水压、压裂孔径等相关参数进行设计，使得水力压裂的增透效果达到最佳。