宽速域飞翼布局后缘射流滚转控制研究

邵 帅，郭 正，贾高伟，阴 鹏，侯中喜，张来平

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 军事科学院 国防科技创新研究院， 北京 100071)

近年来，各军事强国相继推出飞翼布局隐身无人战机的技术验证机型，包括法国的“神经元”，英国的“雷神”，俄罗斯的“猎人”，中国的攻击-11，美国的“幻影雷”、X-45A、X-47A和X-47B等[1]。飞翼布局具备优良的气动特性与隐身性能，但在机动和配平过程中，传统舵面的偏转将破坏飞翼布局的电磁隐身外形。同时舵面的使用增加了飞行器外模线上的开孔和狭缝，增大了雷达散射截面(radar cross section, RCS)。

后缘环量控制射流是指在机翼后缘沿切向射出一股流动。根据柯恩达效应，射流附着于后缘凸曲面，即柯恩达表面，并夹带边界层流动同样绕柯恩达表面偏转一定角度。流线的偏转使翼型产生气动型弯曲，从而改变翼型的环量和升力。左右机翼后缘不同射流组合方式可实现不同姿态控制，其中以滚转控制效果最佳。后缘环量控制射流作为一种典型的主动流动控制技术，具备代替传统舵面进行姿态控制的潜力[2]。

相比舵面，后缘环量控制射流应用于飞行器姿态控制具备诸多优势[2-4]。首先，无须液压传动和铰链机构，射流系统体积小质量轻，可为飞行器增大装载或增加航程。其次，姿态控制设备的零部件数量大幅度减小，提高了系统可靠性，进而提升了飞行器的出勤率。最重要的是活动部件减少，使得外模线更加光滑，机动和配平过程中无舵面偏转，有望大幅改善飞翼布局的动态隐身特性。但同时环量控制设备需从独立气泵或者发动机的压气机引气获得高压气源，将持续消耗能量并对发动机推力产生影响。此外，多项研究表明，随来流马赫数的增大，射流出口激波和边界层的相互作用[5]使射流更易脱离柯恩达表面，导致Cμ失速现象提前发生，环量控制效果[6-9]显著弱化。

尽管多数研究强调射流控制对飞行器隐身性能的显著提升，但鲜有关于射流与舵面控制构型RCS特性的对比研究和量化评估工作。此外，引气导致的推力损失评估也少见于文献研究。针对飞翼布局的飞行试验[10-15]、风洞试验[2-3]和数值模拟[16-17]工作多关注低速时利用环量控制技术进行部分姿态控制(以滚转控制为主)的可行性。仅Forster[18]通过数值模拟确认了高亚声速(Ma=0.7)中飞翼布局SACCON(stability and control configuration)的机身内侧射流与舵偏10°产生的控制力矩接近。飞翼布局隐身无人战机的实际飞行速度涵盖了低速至高亚声速，在宽速域范围环量控制技术用于飞翼布局滚转控制的可行性有待进一步验证。

因此本文结合气动和隐身数值计算方法，在宽速域范围(Ma为0.145～0.7)内系统性研究后缘环量控制射流对飞翼布局的滚转控制效果，并与传统舵面控制构型进行对比。研究关注电磁隐身特性、滚转控制特性、流动机理分析和射流引气影响四个方面。同时在射流引气影响小节中，提出控制效率因子参数对比射流与舵面的控制效率。本文期望为射流主动流动控制无操纵面飞翼布局飞行器的设计工作提供量化参考依据。

1 研究对象

MULDICON(multi-disciplinary configuration)布局[19]由北约AVT-251任务组提出，如图1所示，本文将其作为滚转控制研究的飞翼平台。参考长度为cref=6 m，参考面积为Sref=77.8 m2，力矩参考点(moment reference point, MRP)坐标为(x,y,z)ref=(6,0,0) m。其控制舵面包括内侧舵面(inner board, IB)和外侧舵面(outer board, OB)。舵面控制构型的几何模型如图2所示。单个舵面的面积为1.16%参考面积。舵面后缘下偏为正。

图1 MULDICON布局几何外形Fig.1 Geometry of MULDICON

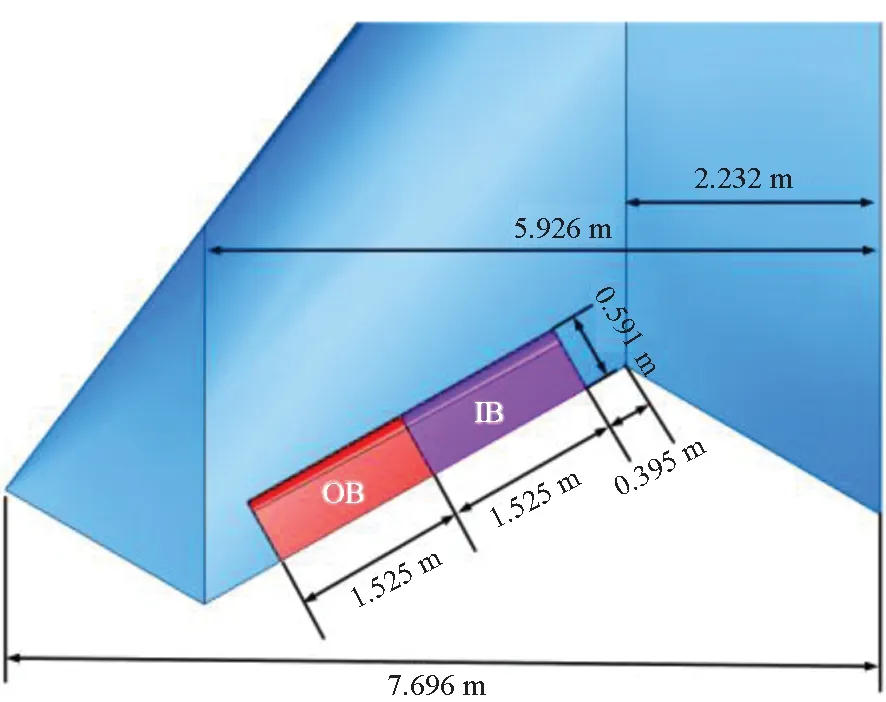
图2 舵面控制构型的几何模型Fig.2 Geometry of the flying wing with control surfaces

为保证可比性，将内外侧舵面在后缘上的相应位置分别替换为环量控制设备，得到射流控制构型。Michie[20]研究得到高效环量控制设备的几何比例，本文据此对外翼段后缘修型，比例参数如图3所示。每个环量控制设备均有上下两个射流出口，使用IUJ、ILJ、OUJ和OLJ分别代表内侧上、内侧下、外侧上和外侧下四个出口的射流。

图3 射流控制构型的几何模型Fig.3 Geometry of the flying wing with CC jets

考虑对称性，本文以向右滚转为例研究不同控制设备的滚转控制效果。舵面控制时，左右机翼外侧舵面差动偏转δOB分别为±10°、±20°(左机翼OB后缘下偏，右机翼OB后缘上偏)，为方便表述对应构型在后文分别简称为舵偏10°构型和舵偏20°构型。使用舵面控制但舵面无偏转时(即δOB=±0°)，简称无舵偏构型。射流控制时，左右机翼外侧环量控制设备差动射流(左机翼OUJ和右机翼OLJ射流开启)。

2 数值方法及验证

2.1 气动计算方法及验证

气动数值模拟使用非结构混合网格计算流体力学仿真软件HyperFLOW[21-22]。计算中，无黏通量离散使用Roe格式，黏性项使用法向导数法离散，湍流模型采用k-ωSST两方程模型。使用MULDICON布局和椭圆环量控制翼模型分别验证HyperFLOW准确模拟飞翼布局绕流和环量控制翼绕流的能力。

2.1.1 飞翼布局绕流算例验证

验证分为两步，首先进行网格无关性验证得到后续研究的网格基础，接着在一定迎角范围内与文献对比气动载荷结果，验证气动力和力矩的准确性。

验证算例来流条件为马赫数Ma=0.4, 每米雷诺数Re=9.333×106。计算网格为非结构混合网格，物面为40层棱柱网格，外部空间由四面体网格填充，机身周围区域进行适当加密。表1列出了三套网格的参数，图 4展示了中等密度网格细节，三套网格的拓扑结构相同。表2展示了网格加密对气动载荷的影响，迎角α=0°，从中等密度网格到密网格，升力系数CL、阻力系数CD和俯仰力矩系数Cm的变化微小，故选择中等密度网格开展后续研究。图5展示了HyperFLOW求解器与采用SA-neg(negative sparlart-allmaras turbulance model)湍流模型的德国宇航中心DLR Tau求解器[23]对MULDICON布局的气动特性预测结果。两者的CL和CD曲线吻合良好，Cm曲线在小迎角时吻合良好，当迎角大于6°后由于湍流模型的差异而存在偏差，但变化趋势一致。本文关注小迎角附近来流速度和射流强度对滚转控制效果的影响，因此计算方法可用于后文飞翼布局气动特性的评估工作。

表1 MULDICON布局网格参数Tab.1 Details of grids of MULDICON

图4 MULDICON布局网格剖分Fig.4 Grid of MULDICON

表2 网格加密对气动载荷的影响Tab.2 Influence of grid refinement on aerodynamic loads

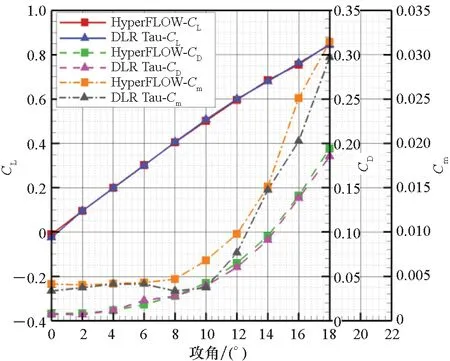
图5 MULDICON布局气动特性Fig.5 Aerodynamic characteristics of MULDICON

2.1.2 椭圆环量控制翼算例验证

椭圆环量控制翼模型风洞试验[8]覆盖了低速到跨声速，是环量控制翼的标准验证算例之一。来流条件为Ma=0.3，Rec=1×106,α=3°和Ma=0.8，Rec=2.5×106,α=3°(Rec为基于翼型弦长的雷诺数)。翼型剖面如图 6(a)所示，试验模型和网格如图 6(b)所示，模型展长为弦长的2倍，蓝色为端板以减少有限展长的三维效应，黄色为支撑模型的分流板作黏性壁面考虑[8]。机翼表面和气室内部的结构网格参考文献[9]的剖分方式。机翼表面和柯恩达表面法向第一层网格厚度分别为1×10-5c和5×10-6c，以保证y+～Ο(1)。

(a) 翼型剖面(a) Airfoil section

(b) 网格(b) Grid图6 椭圆环量控制翼的几何和网格Fig.6 Geometry and grid of the elliptical CC airfoil

环量控制设备的高压气室前壁面使用压力入口边界条件，如图 6(a)所示，总压p0,plenum通过压比NPR=p0,plenum/p∞设置，总温T0,plenum=T∞，p∞和T∞分别为来流压力和温度，速度方向与边界面垂直。射流动量系数Cμ是环量控制的重要无量纲参数，表征射流动量与来流动压的相对大小，定义如下：

(1)

(2)

其中，下标b为边界值，pc为动量修正的压力值。将压力入口边界视为常规壁面积分压力和黏性切应力，进而得到修正的整机气动力和力矩。

图7展示了椭圆环量控制翼的压力系数Cp云图和展向中间截面(Z=1)的流线图，流线用Cp着色。从截面流线可以看出，射流作用下绕流偏转显著，翼型产生气动型弯曲。Ma=0.8时，机翼背风面出现激波。此外，由于两端受到端板和分流板的影响，表面Cp分布存在展向差异，因此积分展向中间截面的压力系数作为翼型的升力系数。

(a) Ma=0.3， Cμ=0.054

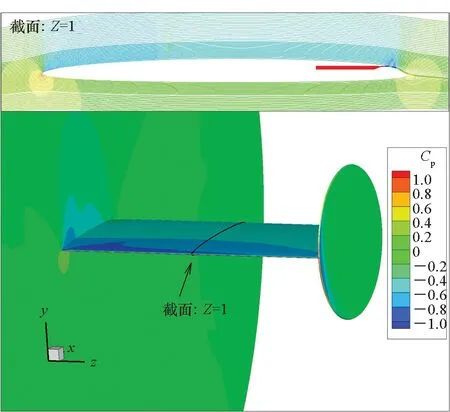
(b) Ma=0.8， Cμ=0.008图7 椭圆环量控制翼绕流流场Fig.7 Flow field over the elliptical CC airfoil

图8为展向中间截面升力系数增量ΔCL计算值与试验值[8]的对比。表 3列出了计算值与试验值的偏差。Ma=0.3与Ma=0.8且Cμ较小时，计算值与试验值吻合良好。Ma=0.8且Cμ较大时，计算值与试验值的最大相对偏差为16.96%，远小于环量控制翼文献中常见的升力系数25%的偏差[24]。因此，本文的计算方法能够满足宽速域环量控制翼的数值模拟需求。

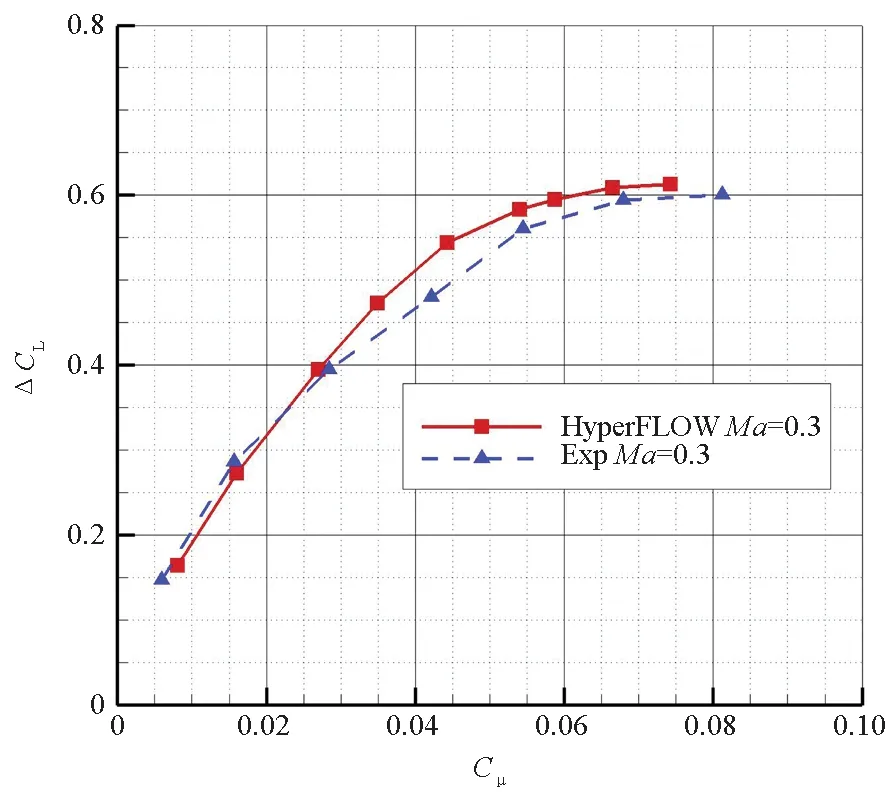
(a) Ma=0.3， Rec=1×106, α=3°

(b) Ma=0.8， Rec=2.5×106, α=3°图8 展向中间截面增升效果Fig.8 Lift augmentation of the midspan wing section

表3 ΔCL计算值与试验值的偏差Tab.3 Deviation between computational and experimental ΔCL

2.2 隐身计算方法及验证

X波段(8～12.5 GHz)是机载火控雷达的主要工作频段，且在针对飞行器的雷达中占比最大[25]。故本文选择10 GHz典型频点研究射流控制对飞翼布局隐身性能的提升。电尺寸是RCS数值模拟中的重要指标，是目标尺寸与雷达工作波长之比，用以选择合适的数值计算方法准确高效地完成RCS数值计算。MULDICON的尺寸相对10 GHz频点为超电大尺寸，因此采用大面元物理光学法(large element physical optics, LEPO)进行数值模拟。采用经典金属圆柱体模型对LEPO方法进行验证。圆柱模型和计算设置如图9所示。

图9 金属圆柱体RCS计算与试验数据对比Fig.9 Comparison between experimental and computational RCS results of a metal cylinder

图9表明各个方位的RCS计算值与试验数据[26]均吻合良好，即LEPO方法能够较为准确地模拟金属圆柱体等凸结构的电磁散射特性，因此该方法能够满足超电大尺寸飞翼布局的RCS数值模拟需求。

3 结果分析

3.1 电磁隐身特性

滚转控制时，飞行器将发生姿态变化，电磁隐身特性将随之显著变化。因此，本文将同时考虑滚转角φ=0°和φ=10°时射流和舵面控制构型的RCS散射特性。绝大多数空中机载火控雷达采用垂直极化(vertical polarization, VV)工作方式，本文模拟也采用这种极化方式。电磁波入射频率10 GHz，入射角度θ为0°～360°。射流和舵面控制构型的隐身计算网格的网格量分别为274万和237万。图10展示了数值模拟中的雷达波入射角度。

图10 飞翼布局雷达波入射示意图Fig.10 Radar irradiation on the flying wing

图11展示了无舵偏构型在滚转角φ=0°状态下的RCS散射图。该构型具有对称性，在θ为0°～180°方位内存在四个强散射点，其中三个为θ=53°的垂直前缘方向、θ=90°的翼尖方向、θ=150°的垂直外翼段后缘方向。第4个强散射点在θ=120°方位，此方位上舵面转轴缝隙充分暴露，形成较强的电磁波散射。图 12对比了φ=0°时射流控制构型、无舵偏构型和舵偏20°构型的RCS散射特性。在θ为53°、 90°、 150°三个方位和其对称方位上，三种构型的RCS峰值大小无明显差异。但在θ=120°和θ=240°方位，相比无舵偏构型，射流控制构型的RCS显著减小，舵偏20°构型的RCS显著增大。在θ=120°和θ=240°方位附近，以射流控制构型RCS值小于舵面控制构型时的方位角范围标示出角域1和角域2，代表舵面控制导致的峰值宽度，在图 12中用黑色矩形标出。表 4对比了三种构型在两个角域和前向威胁扇区(θ为-30°～30°)的RCS均值。在0°滚转角状态下，射流控制显著提升了角域1和角域2内的隐身特性，RCS均值相比舵偏20°构型降幅大于23 dBsm；前向隐身特性也有提升，RCS均值相比舵偏20°构型降幅大于2 dBsm。

图11 φ=0°时无舵偏构型RCS散射图Fig.11 RCS of the flying wing with undeflected control surfaces at φ=0°

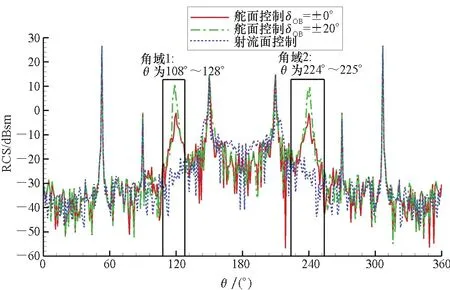
图12 φ=0°时射流与舵面控制构型RCS对比Fig.12 Comparison of RCS of flying wings with CC jets and with control surfaces at φ=0°

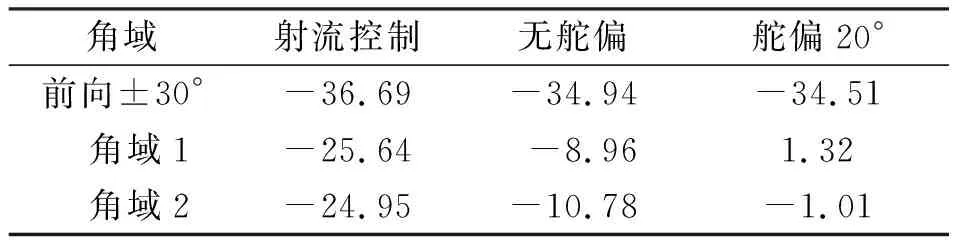
表4 φ=0°时不同构型特定角域的RCS均值对比Tab.4 Mean value of RCS of different configurations at specific azimuth ranges at φ=0° 单位：dBsm

图13展示了无舵偏构型在滚转角φ=10°状态下的RCS散射图。与图 11对比，机身滚转后，电磁散射特性明显改变。机翼前缘和后缘散射产生的RCS峰值显著减小，在θ=90°方位的翼尖散射峰值消失，但前向和侧向的RCS显著增大。同时除θ=120°和θ=240°方位外，θ=60°和θ=300°方位附近出现了新的强散射源。这些散射源均由机身滚转后，舵面脱离机身遮挡而暴露形成。图 14对比了φ=10°时射流控制构型、无舵偏构型和舵偏20°构型的RCS散射特性。采用与图12同样的方法标识出4个RCS峰值的角域3～6。在这些角域内，射流控制构型同样显著减小了RCS峰值大小。统计这些角域和前向威胁扇区的RCS均值，如表5所示。在10°滚转角状态下，射流控制相比舵偏20°构型同时提升了角域3～6和前向的隐身特性，RCS均值降幅分别大于18 dBsm和3 dBsm。

图13 φ=10°时无舵偏构型RCS散射图Fig.13 RCS of the flying wing with undeflected control surfaces at φ=10°

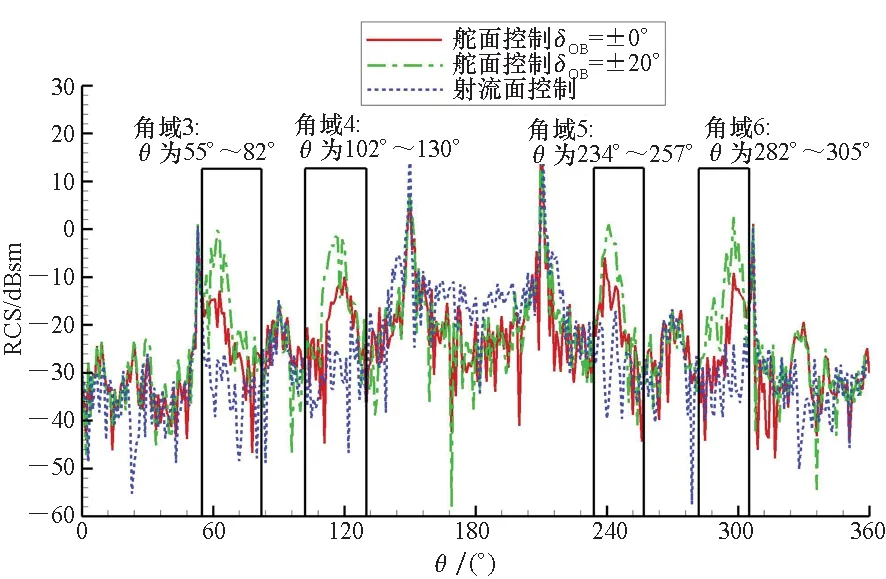
图14 φ=10°时射流与舵面控制构型RCS对比Fig.14 Comparison of RCS of flying wings with CC jets and with control surfaces at φ=10°

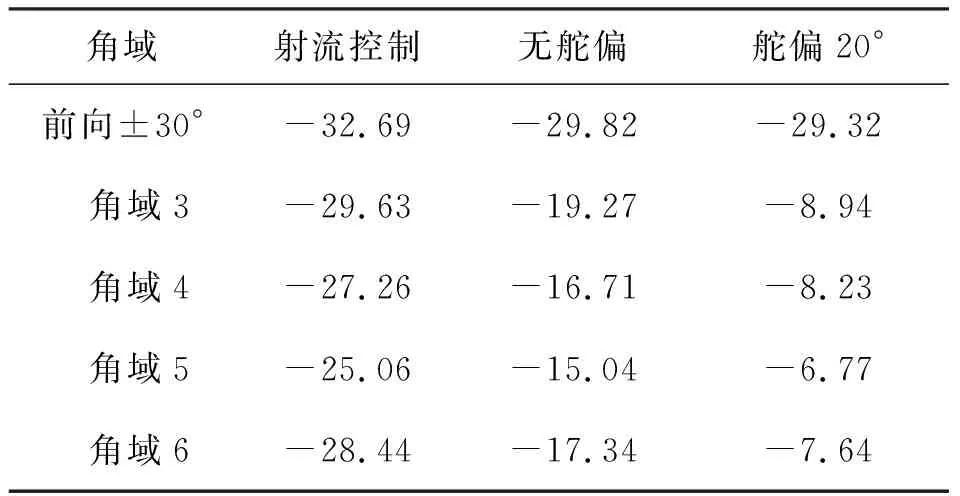
表5 φ=10°时不同构型特定角域的RCS均值对比Tab.5 Mean value of RCS of different configurations at specific azimuth ranges at φ=10° 单位：dBsm

3.2 滚转控制特性

在干净布局的中等密度网格基础上划分舵面和射流控制构型的网格，如图15和图16所示。环量控制设备气室内部和柯恩达表面区域使用结构网格进行剖分，柯恩达表面第一层网格厚度为3×10-6m，以确保y+～Ο(1)。计算中来流速度覆盖低速至高亚声速，马赫数分别为0.145、0.4和0.7，对应的每米雷诺数分别为Re=3.3×106、Re=9.333×106和Re=1.881×107，迎角均为0°。所研究的射流压比范围为NPR为1.1～3。

图15 舵面控制构型的网格剖分Fig.15 Cell of the flying wing with control surfaces

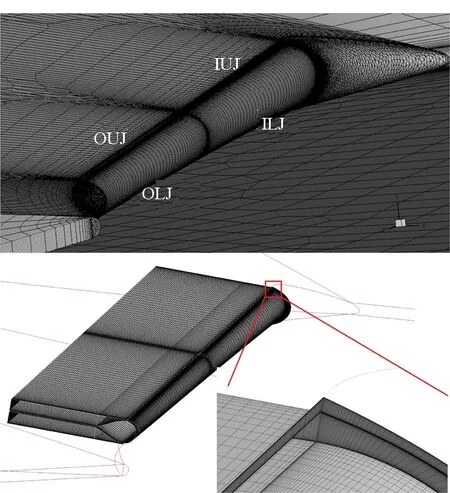
图16 射流控制构型的网格剖分Fig.16 Cell of the flying wing with CC jets

图17为不同马赫数下，射流控制时滚转力矩系数增量ΔCl=Cl-Cl0随Cμ的变化。当Ma≥0.4时，ΔCl随Cμ线性增长到最大值后下降；当Ma=0.145时，Cμ增大至0.013后，ΔCl仍然保持增长趋势。为方便表述，将此时的滚转力矩增量视为所研究压比范围内ΔCl的最大值。表 6列出了射流滚转控制特性系数，其中射流滚转控制舵效∂Cl/∂Cμ由图 17中曲线的线性段作最小二乘估计得到。随马赫数的增大，射流控制可产生的滚转力矩系数最大值(ΔCl)max显著减小，来流马赫数从0.145增至0.4时，(ΔCl)max降至低速时的56%；马赫数继续增大到0.7时，进一步减小至低速时的23%。但Ma=0.4和Ma=0.7时的射流舵效较为接近，均超过Ma=0.145的15倍。

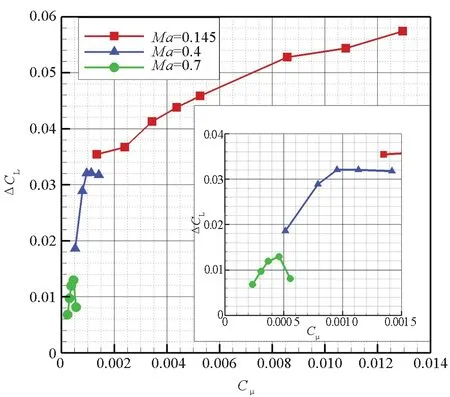
图17 滚转力矩系数增量随Cμ的变化Fig.17 Changes of increasements of roll moment coefficients due to Cμ variation

表6 射流滚转控制特性系数Tab.6 Roll control characteristics of the CC jet

图18对比了宽速域下射流控制与舵面控制的滚转力矩系数增量。随来流速度增大，射流能够产生的滚转控制力矩系数显著减小，舵面的滚转控制力矩系数却有小幅增长。具体来看Ma=0.145、Ma=0.4和Ma=0.7时，在所研究的射流压比范围内，后缘环量控制射流产生的(ΔCl)max分别约为舵偏20°的2.7倍、1.3倍和0.5倍。同时Ma=0.7时，射流的(ΔCl)max仍能达到舵偏10°的1.2倍。

图18 射流与舵面控制滚转力矩系数增量对比Fig.18 Comparison of increasements of roll moment coefficients of the CC jet and control surface

飞翼布局使用传统舵面控制时容易产生控制力矩耦合[27]，让飞行器进入非指令耦合运动，控制难度较大。根据不同马赫数下射流与舵面滚转控制能力差异，调整射流强度使射流在Ma为0.145、0.4和0.7时分别产生与舵偏20°、20°和10°相同的滚转力矩系数，进而对比射流与舵面在滚转控制中的力矩耦合特性。

三个射流算例对应的射流条件如表7所示。图19对比了三组射流与舵面控制算例的力矩耦合特性。Ma=0.145时，射流滚转控制产生的耦合俯仰力矩和偏航力矩分别比舵面偏小93%和15%；Ma=0.4时，射流相比舵面的耦合俯仰力矩和偏航力矩分别偏大169%和139%；Ma=0.7时，射流控制的耦合力矩略微偏大。整体来看，射流滚转控制时力矩耦合特性受马赫数影响显著，与舵面相比，低速时横向与纵向和航向力矩耦合减弱，高速时力矩耦合增强。

表7 与舵面滚转力矩相同时的射流条件Tab.7 Jet conditions when the CC jet produces the same roll moment coefficient as a control surface

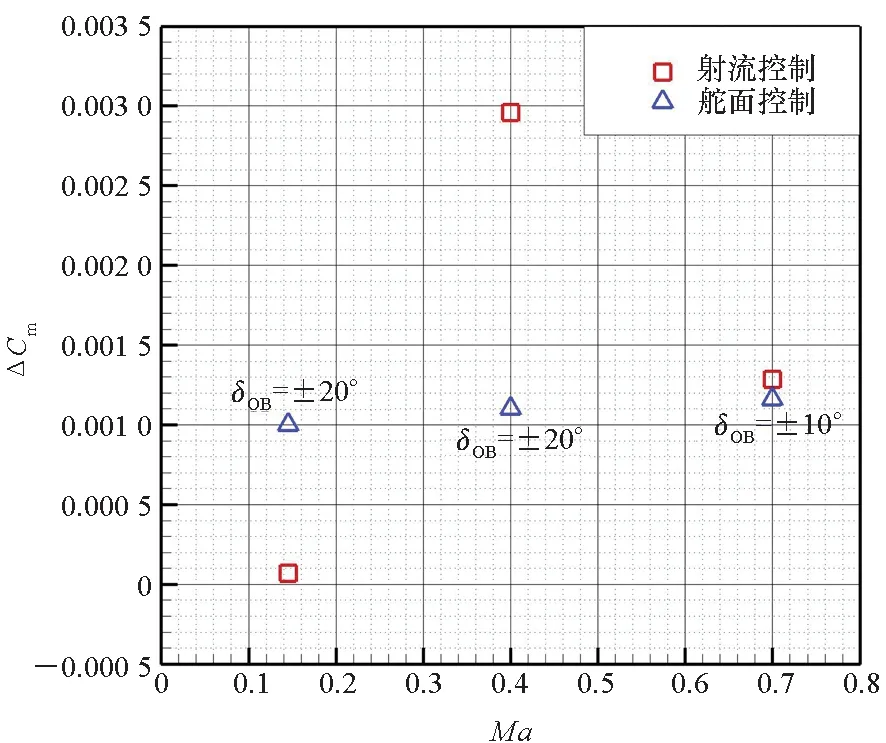
(a) ΔCm-Ma

(b) ΔCn-Ma图19 射流与舵面控制的力矩耦合特性对比Fig.19 Comparison of moment coupling characteristics between the CC jet and control surface

3.3 流动机理分析

滚转控制方面，低速时射流比舵面控制能力强，但来流速度增大后控制能力显著下降。本节通过分析流动结构和压力分布，以揭示背后的流动机理。

图 20展示了射流控制得到最大滚转力矩时全机压力分布和外翼段绕流。以右侧机翼后缘绕流为例做进一步分析，如图 21所示。两图中红色和蓝色流线分别为射流和机身绕流流线。Ma=0.145时，最大滚转力矩对应的射流压比NPR=3，射流在出口处于欠膨胀状态，不断膨胀和压缩形成一系列马赫盘，如图 21(a)所示。射流绕过柯恩达表面来到上表面，此时仍未充分膨胀，压力较高，因此在上表面后缘形成一片沿展向分布的高压区域，如图 21(b)所示。射流在上表面继续向上游流动，阻滞上表面来流形成大范围流动分离。分离区上游形成高压区，分离区下方则形成低压区。射流方向垂直机翼后缘(后掠角30°)，速度存在展向分量，因此射流脱离壁面向下游折返的同时向翼梢方向流动并汇入尾迹，如图 20(a)所示。射流与绕流的相互作用区域覆盖整个外翼段外侧和翼梢区域。该区域远离对称面，延长了横向操纵力臂，并且局部压力系数Cp变化幅度较大，因此低速时射流控制产生了较强的滚转控制效果。

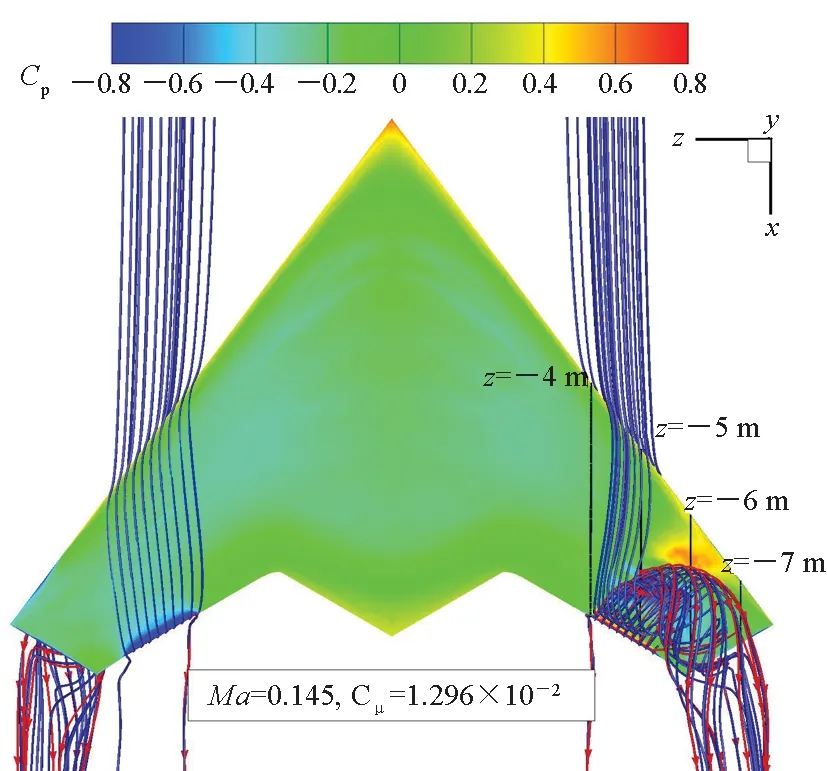
(a) Ma=0.145, 上表面(a) Ma=0.145, upper surface

(b) Ma=0.4, 上表面(b) Ma=0.4, upper surface

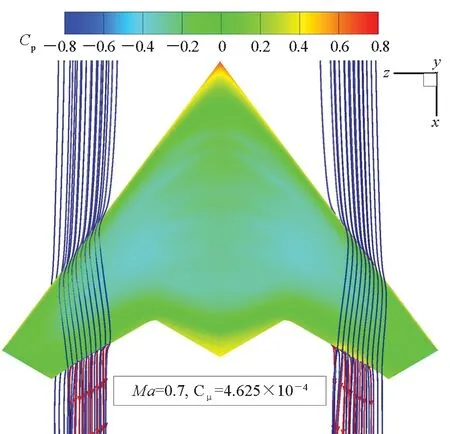
(c) Ma=0.7, 上表面(c) Ma=0.7, upper surface

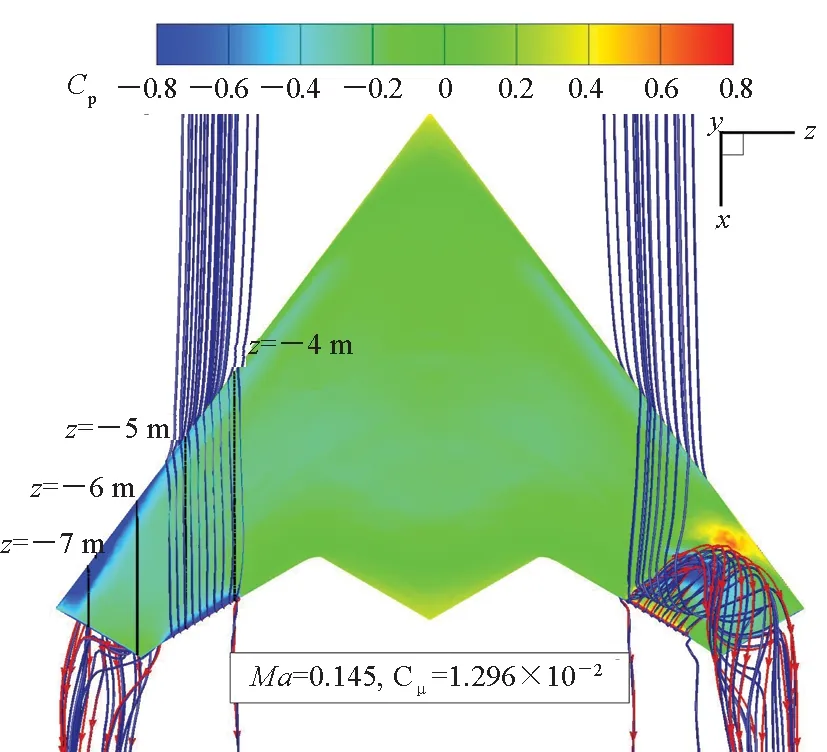
(d) Ma=0.145, 下表面(d) Ma=0.145, lower surface

(e) Ma=0.4, 下表面(e) Ma=0.4, lower surface

(f) Ma=0.7, 下表面(f) Ma=0.7, lower surface图20 射流滚转控制时Cp分布和绕流流场Fig.20 Cp distributions and flow fields of the flying wing with CC jets for roll control

(a) Ma=0.145, Ma云图(a) Ma=0.145, contours of Ma

(b) Ma=0.145, 后缘绕流(b) Ma=0.145, flow over trailing edge

(c) Ma=0.4, contours of Ma(c)Ma=0.4, Ma云图

(d) Ma=0.4, 后缘绕流(d) Ma=0.4, flow over trailing edge

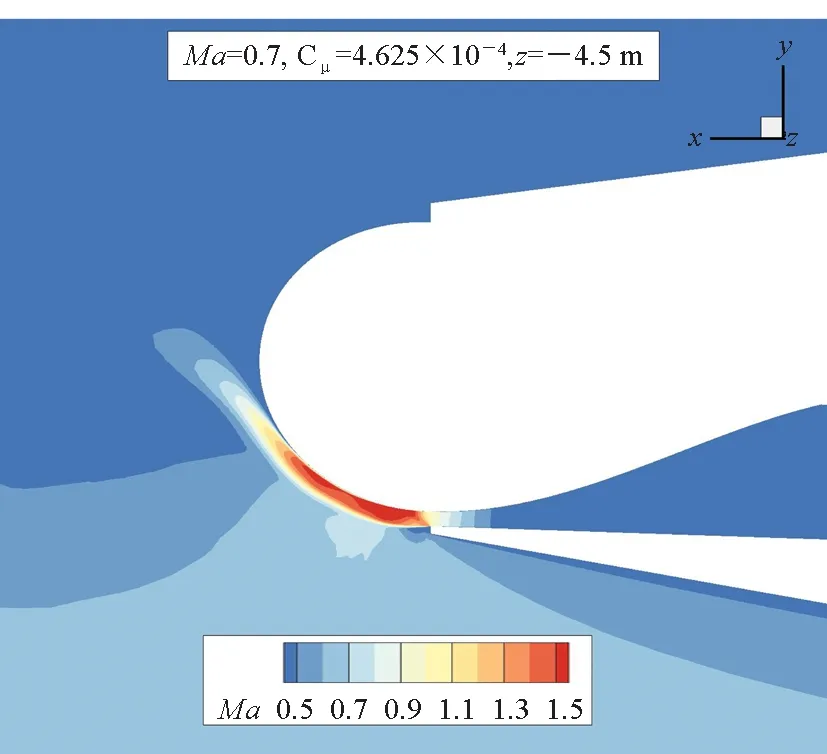
(e) Ma=0.7, Ma云图(e) Ma=0.7, contours of Ma

(f) Ma=0.7, 后缘绕流(f) Ma=0.7, flow over trailing edge图21 右侧机翼后缘绕流和z=-4.5 m截面Ma云图Fig.21 Flow fields over right wing′s trailing edge and Mach number contours on z=-4.5 m section

马赫数增大至0.4后，最大滚转力矩对应的射流压比NPR=2，射流在出口处于轻微的欠膨胀状态，膨胀加速后超过声速，如图21(c)所示。靠近机身内侧3/4的射流保持附着，靠近翼梢1/4的射流提前与柯恩达表面分离，如图 21(d)所示。保持附着的射流绕至上表面后，压力已经较小，在上表面向上游前进较短距离后便折返向下游流动。上表面来流受到射流阻挡在后缘形成小范围的分离区，Cp受影响的区域也集中于此(4 m≤|z|≤6 m)，如图 20(b)所示。马赫数继续增大至0.7，压比NPR=2.5，欠膨胀射流在出口形成马赫盘，绕柯恩达表面偏转大约60°后脱离，如图 21(e)所示。射流脱离曲面后形成“气幕”，对来流形成一定阻挡，导致上表面后缘出现小范围的高压区，如图 21(c)和图21(f)所示。从Ma=0.4到Ma=0.7，射流对机身表面Cp的影响区域在弦向进一步缩窄，仅限于极靠近后缘的区域。同时对比图 20(d)、图20(e)、图20(f)所示的右机翼下表面后缘，射流对下表面边界层流动存在剪切加速作用，使后缘出现低压区，低压区随马赫数增大强度减弱且范围缩小。总结来看，随来流速度增大，存在两个效应使得射流滚转控制能力下降：①射流从翼梢端开始提前脱离柯恩达曲面，对对侧边界层流动的阻滞效应减弱；②射流与来流速度差减小，对同侧边界层的夹带效应减弱。

图22展示了图20中z=-4 m、 -5 m、 -6 m、 -7 m四个典型截面的Cp分布。其中Ma=0.145和Ma=0.4时，z=-5 m截面上表面后缘Cp大幅波动对应于射流绕至上表面迫使上表面来流发生分离。z=-6 m和z=-7 m截面上，Ma=0.145的Cp分布与另外两组Cp分布存在显著差异。其上表面后缘存在较大范围的低压平台，这是因为射流导致的流动分离区覆盖了翼梢区域。马赫数增大至0.4后，射流对下表面流动夹带效应和对上表面流动的阻滞效应减弱，对机身绕流的影响范围限于后缘附近，对z=-7 m截面Cp分布的影响也几乎消失。

(a) z=-4 m

(b) z=-5 m

(c) z=-6 m

(d) z=-7 m图22 射流滚转控制时四个典型截面Cp分布Fig.22 Cp distributions on four sections in cases of CC jets for roll control

3.4 射流引气影响

本节将从推力损失和压气设备功率系数两方面综合评估射流引气的影响，并将压气耗能转化为阻力，提出控制效率因子，对比射流与舵面的滚转控制效率。

接着考虑环量控制所需压气设备的功率系数。环量控制通过独立气泵或者发动机的压气机获得高压气源，需持续消耗能量维持射流。压气耗能的功率系数Pc,jet可以用如下公式[30]计算：

(3)

(4)

结合等熵过程总温与静温及总压与静压关系,式(3)可转化为：

(5)

其中：T0,∞和p0,∞分别为来流总温和总压；ρ∞和u∞分别为来流密度和速度；cp为等压热容；η为压气设备效率，这里设定为η=85%。

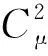
图23 射流滚转控制压气设备功率系数随Cμ的变化Fig.23 Changes of pump′s power coefficients due to Cμ variation in cases of CC jets for roll control

最后提出控制效率因子表征单位阻力系数获得的滚转力矩系数改变量。舵面的控制效率因子定义如下：

(6)

式中，|Cl-Cl0|和CD-CD0分别为设备产生的滚转力矩系数改变量和伴生的附加阻力系数。

类比文献[30]将压气耗能等效为阻力并修正升阻比的做法，本文将压气设备功率系数视为额外阻力系数，修正射流的控制效率因子为：

(7)

式中：CD-CD0为增大后缘厚度(增大阻力)与射流反冲作用(减少阻力)对阻力系数的综合影响，压气耗能的功率系数Pc,jet在这里被视为附加阻力系数。

图 24对比了两种控制方式的滚转控制效率因子。Ma=0.145时，射流控制效率整体小于较高马赫数下的效率；Ma≤0.4时，射流控制效率随Cμ增大而减小；Ma=0.7时，射流控制效率随Cμ先上升后下降。与射流控制不同的是，舵面控制时偏转角度越大控制效率越高。但在所研究的Cμ范围内，Ma≥0.4时射流的控制效率始终高于舵偏20°的控制效率。在Ma=0.145时，射流控制效率随Cμ增大而下降，依次低于外侧舵面差动偏转20°和10°的效率。若考虑表7中的三个算例，即环量控制射流产生舵偏20°(Ma≤0.4)和10°(Ma=0.7)的滚转力矩时，射流的控制效率均高于舵面。

图24 滚转控制时射流与舵面控制效率因子对比Fig.24 Comparison of control efficiency factors of the CC jet and control surface for roll control

4 结论

本文针对利用后缘环量控制射流进行滚转控制的宽速域飞翼布局飞行器，系统性研究了其电磁隐身特性、滚转控制特性和相关流动机理，以及射流引气的综合影响，得出以下结论：

1)舵面控制构型由于存在转轴缝隙和舵面偏转，滚转角为0°和10°时，60°、120°、240°和300°方位附近角域将出现RCS峰值。射流控制可显著提升这些方位的隐身特性，对比舵偏20°构型RCS均值降幅大于18 dBsm。同时射流控制对前向威胁扇区(θ=-30°～30°)的隐身特性也有提升，对比舵偏20°构型RCS均值降幅大于2 dBsm。

2)在Ma=0.145～0.7的宽速域范围内，随马赫数的增大，射流提前与柯恩达表面分离，对边界层流动的阻滞和夹带效应减弱，导致滚转控制能力显著下降，但射流舵效∂Cl/∂Cμ显著提升。Ma=0.145、Ma=0.4和Ma=0.7时，射流控制能够产生的最大滚转力矩分别约为舵偏20°的2.7倍、1.3倍和0.5倍。Ma≥0.4时射流控制舵效约为Ma=0.145时的15倍。射流与舵面控制相比，低速时横向与纵向和航向力矩耦合减弱，Ma≥0.4时力矩耦合增强。

3)压气设备功率系数随Cμ呈二次函数关系增长，且增长率随来流马赫数增大。控制效率因子将压气耗能考虑为额外阻力，能够有效对比射流和舵面的控制效率。射流产生舵偏20°(Ma≤0.4)和10°(Ma=0.7)的滚转力矩时，引气量小于发动机进气量的1.82%，对应的推力损失不超过1.62%，射流的控制效率均比舵面更高。

4)综合来看，虽然后缘环量控制射流的滚转控制能力随马赫数增大而显著下降，但Ma=0.7时射流控制仍能达到舵偏10°的滚转控制效果。同时射流控制大幅提高了典型角域的电磁隐身特性，引气量少，推力损失小，控制效率因子高。因此，后缘环量控制射流是一种极具潜力的飞翼布局滚转控制设备。