基于增量非线性动态逆的液压执行器力控制策略研究

解占新，闫 政

(晋中学院 机械系，山西 晋中 030619)

引言

液压驱动相比电机驱动，有更高的功率重量比和刚度，广泛应用于重型机械臂[1]、足式机器人[2]和助力系统[3]。液压执行器具有高度的动力学非线性和模型不确定等特性，使得液压驱动的系统高精度运动控制成为研究热点。液压执行器通过伺服阀控制流量，以速度指令作为输入控制运动。但机器人关节执行器是以关节电流作为输入直接控制力，即力矩控制，此差异化使得当前广泛研究的机器人控制技术[4]无法直接应用于液压驱动的机器人。因此，需要将液压机器人的控制器级联成一个多回路结构去解决电液联合控制问题。具体方法是，内环为压力反馈解耦的力跟踪控制器，跟踪外环运动控制器给出的期望驱动力。级联的优势是可以在外环运动控制中采用当前成熟且先进的电驱机器人控制技术，内环只需专注高性能的力跟踪控制器研究。

由于液压执行器的高度非线性动力学、模型简化以及参数动态变化导致的模型不确定，使得液压执行器的高性能力控制具有挑战性。文献[5]指出，一般的线性控制器，如Proportion Integration Differentiation(PID)[6,7]在此类应用中受到带宽限制，导致显著的相位滞后，并随着频率的增加而恶化，根本不能实现液压执行器高性能的力控需求。这就需要更先进的基于模型的控制方案(Model-Based Control，MBD)，如反馈线性化[1,8]及其变体，包括基于非线性动态逆(Nonlinear Dynamic Inversion，NDI)的控制[9-11]，级联压力控制(Cascade ΔPController，CdP)[12]和平坦控制(Flatness-Based Control，FBC)[13]。然而，MBD性能严重依赖于被控对象的精确模型，在参数不匹配的情况下性能恶化严重。

增量非线性动态逆(Incremental Nonlinear Dynamic Inversion，INDI)[14]是一种基于传感器的非线性控制技术，只对系统标称模型的部分进行反馈线性化，解决了传统反馈线性化固有的完整模型依赖问题。文献[15-16]已经验证了在高采样率的条件下，在飞控系统中INDI可以实现优秀的控制性能和鲁棒性。在与液压相关的机器人系统高精度控制方面，INDI具有以下优势：

(1) 对模型参数不确定性和连续外部干扰，无需设计明确的自适应或鲁棒控制算法，具有固有的鲁棒性；

(2) 控制性能好，计算量小且控制器设计简单；

(3) 无需精确的被控对象非线性动力学模型，就能进行系统的反馈线性化设计。

液压执行器的非线性模型不确定问题，许多研究采用非线性自适应控制方法进行处理[17-19]。液压动态参数的自适应控制律设计是与完整的系统控制器设计相结合，以保证全局稳定性。因此，很难直接与不同的外环控制器相结合，而且还会带来高计算负荷等实际问题。因此，高性能、完全解耦和模型依赖性较小的液压力控制器设计与研究显得迫切重要。

本研究讨论了INDI控制技术在典型阀控非对称液压缸形式的执行器和液压挖掘机器人上的初步理论分析和应用。此外，给出INDI的鲁棒特性和稳定性的严格证明。通过仿真对比，验证所提控制器的有效性。

1 液压执行器动力学建模

典型的由伺服阀驱动直线非对称缸的液压执行器基本结构如图1所示[20]，A腔室和B腔室的压力动态方程可描述如下：

图1 液压执行器模型Fig.1 Hydraulic actuator model

式中，pa和pb——分别是执行器的无杆腔和有杆腔的压力

Φa，Φb——伺服阀进出油口的流量

Φlp——内泄漏流量

Aa，Ab——分别是执行器的无杆腔和有杆腔的面积

E——油液弹性模量

xp——执行器位移

Lc——执行器总的有效行程

Vpl——容腔的管路体积

执行器的液压力Fh由执行器A和B腔中产生的压力平衡形成，即：

Fh=paAa-pbAb

(2)

取式(2)式微分形式，并带入式(1)，可得：

(3)

其中，取A腔活塞杆面积为Ap，α是活塞面积比率(即，Aa=Ap且Ab=αAp)，Va和Vb分别是考虑各自管路容腔后A和B两腔体积，即Va=Apxp+Vpl，Vb=αAp(Lc-xp)+Vpl。

可以将执行器的每个腔室将定义一个等效传动刚度，即(Ktha=ApE/Va，Kthb=αApE/Vb)，则整个液压缸等效刚度可考虑为2个弹簧并联形式(无论执行器朝哪个方向运动，2个弹簧都呈现出抵抗运动的趋势，因此等效刚度考虑为并联而非串联)，即Kth=Ktha+Kthb=ApE(1/Va+α/Vb)。则：

(4)

其中，Φe=(VbΦa+αVaΦb)/(Vb+αVa)是等效流量，Ae=Ap(Vb+α2Va)/(Vb+αVa)为等效面积。将执行器动态力写成式(4)这种形式，可以显示系统的一个重要物理特性：液压传动刚度Kth，这是动力学中的一个基本物理量。传动刚度越硬，动力传递就越快。传动刚度的先验知识可以为液压机器人的控制和机械设计提供重要的见解[21]。

阀口的流量公式可由如下计算：

(5)

式中，Cd——流量系数

Am——阀门最大面积

xm——阀芯位移

ρ——油液密度

Δp——阀口前后压差

(6)

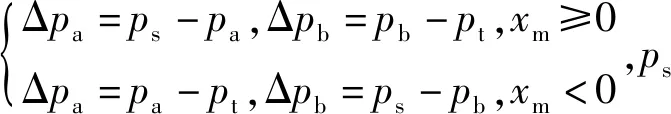
一般阀芯的频率远大于执行器的频率，因此在液压控制的研究中大多忽略了阀芯的动力学，因此可以直接将阀芯位移xm视为系统输入，归一化后为：

(7)

在重型液压装备以及密封要求极高的应用场合，执行器的液压力和输出力并不等同。需要考虑液压缸的摩擦Ff，定义执行器输出力F=Fh-Ff，则完整的液压执行器的动态方程为：

(8)

采用LuGre模型[22]建立液压缸运动系统的摩擦Ff，其数学描述如下：

(9)

式中，σ0——鬃毛刚度

σ1——鬃毛微观阻尼系数

σ2——黏性阻尼系数

z——鬃毛平均变形量

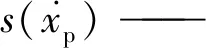
Fc——库伦摩擦力

Fs——最大静摩擦力

vs——Stribeck速度

可以看出，液压缸的摩擦力为速度的非线性函数。

2 增量非线性动态逆

传统的NDI是反馈线性化方法的一种变体，在飞行控制问题中得到了广泛的应用[23]。然而，MBD的常见缺点是严重依赖于被控对象建模的精确度，因此对模型不确定性具有固有的敏感性。INDI本质上是增量形式的NDI方法，除与模型输入相关的其他非线性项的大多数参数影响都通过高采样速率被最小化到一个扰动。因此，INDI并不依赖于精确的建模，对模型的不确定具有天然的不敏感性。

2.1 理论和稳定性

假设被控系统是一般的n阶控制输入的仿射非线性系统，即：

(10)

y=H(x)

(11)

其中,F∈n是系统向量场，u∈m是输入，D∈n是连续的外部扰动，G∈m×n是控制矩阵。假设x，D，H是连续的，F(x)，G(x)是x的∞函数且微分有界。

为简化，设H(x)=x，系统的相对自由度度为(1，…，1)1×n，则系统输出的一阶导数为：

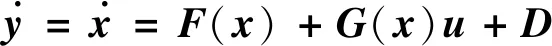
(12)

控制输入u便显式地出现在式(12)中。对于m=n的全驱系统，如果G是可逆的，则可以采用传统的NDI或一般的反馈线性化方法设计控制器，如下：

u=G-1(x)[v-(F(x)+D)]

(13)

可以看出，设计NDI控制率需要精确的系统模型，对系统输入矩阵G，非线性项F和扰动项D都要进行辨识。

INDI与NDI方法不同的是，对式(12)中的系统动力学在每个采样区间的开始时刻(下标为0)泰勒展开，得到系统的增量形式，如下：

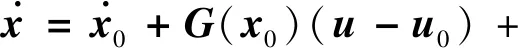
(D-D0)+O(x-x0)2

(14)

用增量形式表示，并将最后三项集中为扰动项：

ΔD+OΔx2

(15)

则式(14)可以表示为：

(16)

利用x和D的连续性以及F和G微分的有界性，计算式(15)在采样时间Ts趋近于0时的极限为：

(17)

式(17)表明，在高采样速率下，式(16)中扰动对系统动力学的贡献趋近于0。因此，在每个采样间隔内，INDI控制律为：

(18)

由此可以看出，INDI相对于NDI不需要对系统非线性项F和扰动项D进行辨识。本质上对于输入矩阵G也无需精确建模，见3.2分析。

设计Lyapunov函数如下：

(19)

其中e=xd-x,xd为期望轨迹。将V(e)求导如下：

δ(Δx，ΔD)]}

(20)

将式(18)代入式(20)，计算得：

(21)

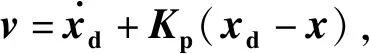
对于输入矩阵不确定的鲁棒性，下面给出证明。

2.2 鲁棒性

考虑式(10)给出的系统，式(18)中的INDI控制律中没有明确使用F和D这些量的信息，因此INDI对F(x)中的参数不确定和连续扰动D不敏感。这两项对系统动力学的贡献可以集中到一个小扰动项中，而扰动项只影响误差动力学的最终界，控制器是全局一致有界稳定，且可以通过增加采样速率来减小到可以忽略的程度。

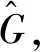
图2 INDI 控制框图Fig.2 INDI control block diagram

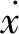
(22)

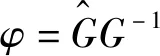
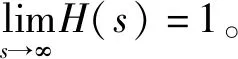
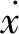
(23)

式(23)表明，传递函数的幅值随着Ts趋近于0而等于0。这与采样周期速率很高时，可以忽略集中扰动项的事实是一致的。

下面考虑MIMO系统。

将INDI控制率带入，同样在高采样速率下忽略集中扰动项，可得系统状态方程：

(24)

对式(24)进行移项变换可得：

(25)

(26)

将式(26)带入式(25)，则系统方程可写成如下对角化形式：

(27)

式(27)可以将系统转化为i个解耦的标量方程：

(28)

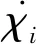
(29)

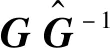
综上证明，INDI是一种非常实用的非线性控制技术，可以克服传统反馈线性化方法对参数不确定性和连续扰动固有的敏感性。

3 控制器设计

3.1 内回路液压力控制器

(30)

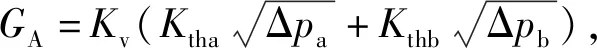
(31)

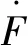
(32)

通过选择一个足够高的采样速率，集中扰动幅度降低到可以忽略不计。然后选择一个简单的线性控制器Kp，将系统变成一个力跟踪控制器，即：

(33)

其中，Fd是期望跟踪的驱动力。

3.2 实施考虑

1) 摩擦力补偿

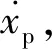
(34)

其中，Fh=(pa-αpb)Ap=pLAp。

2) 二阶滤波器

(35)

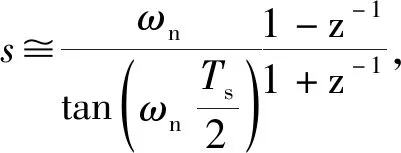
(36)

3) 建模误差容忍度

在INDI控制器中，非线性项ΓA和扰动项D经由高采样速率被消除了，因而不存在于控制率中。而控制输入矩阵GA在模型不匹配程度内(φ>0.5)不会显著影响控制性能，当估计误差过大时，会影响系统稳定性。

GA=

(37)

模型不匹配误差来源主要在于阀，管路和液压缸建模，可通过对GA求梯度进行定性分析。可以看出，阀的流量增益系数Kv和油液弹性模量E对建模影响比较大，在实际中需要谨慎标定。

4 仿真

4.1 仿真环境

建立液压机械臂多物理动态模型，如图3所示，子模块主要包括图4所示的机械臂多体动力学模型，和采用式(1)～式(9)建立的液压执行器数学模型，如图5所示。液压执行器为非对称阀控非对称液压缸，主要参数如表1所示。

表1 液压执行器主要参数Tab.1 Main parameters of hydraulic actuator

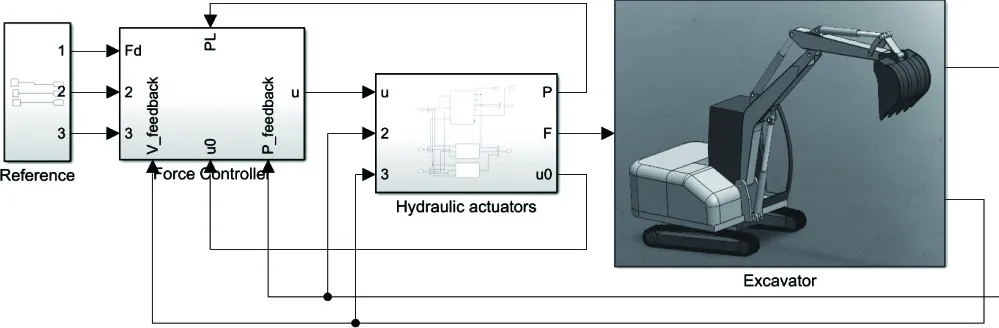
图3 液压机械臂物理仿真模型Fig.3 Physical simulation model of hydraulic robot

图4 机械臂动力学模型Fig.4 Robotic manipulator dynamics model

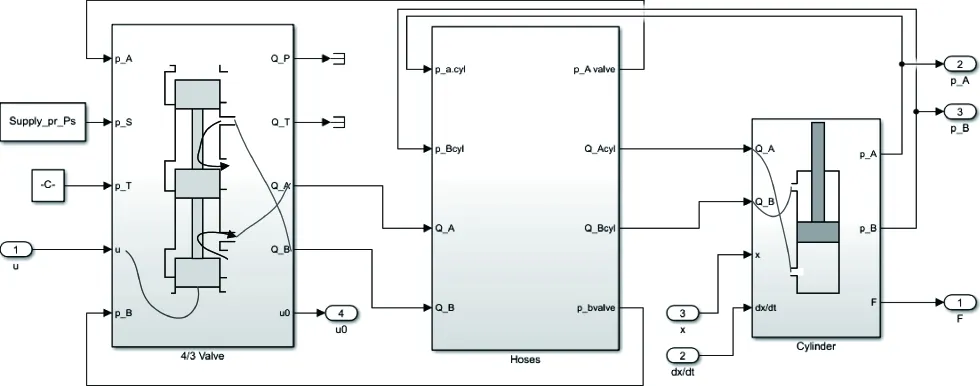
图5 液压执行器动力学模型Fig.5 Hydraulic actuator model

表2 对比控制器主要参数Tab.2 Contrast controller main parameters

4.2 结果与讨论

标称参数模型下PID，NDI和INDI控制器的跟踪性能对比如图6所示。PID和NDI可以观察到明显的跟踪误差，控制器的最大跟踪误差为10%～15%。而INDI具有更准确的跟踪性能，控制器的最大跟踪误差始终在6%左右。因此，INDI的优势已经很明显。

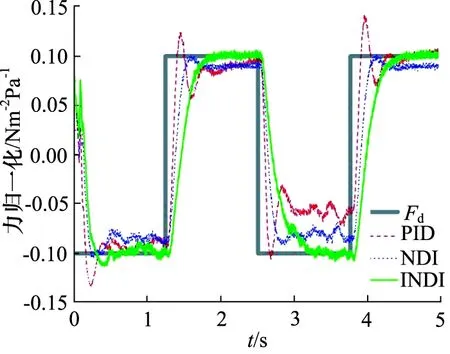
图6 标称模型下力跟踪性能对比Fig.6 Comparison of force tracking performance under nominal model

在实际中，GA的不确定性来源于液压执行器的流量，如参数Kv。本研究中，通过改变Kv参数有意引入模型不匹配程度。INDI，PID和NDI在参数不匹配条件下的力跟踪性能如图7所示。通过与标称模型结果对比，在-40%的GA不匹配程度下，NDI和PID控制器的跟踪性能显著下降，已经无法跟踪设定值，而INDI控制器的性能几乎保持完好。其原因是，NDI的严重依赖于被控对象建模的精确度，因此对模型不确定性具有固有的敏感性。INDI本质上是增量形式的NDI方法，除与模型输入相关的其他非线性项的大多数参数影响都通过高采样速率被最小化到一个扰动。因此，INDI并不依赖于精确的建模，对模型的不确定具有天然的不敏感性。而PID是一种数据驱动的控制策略，对于模型不确定具有一定鲁棒性，但是针对复杂的非线性系统，不能实现液压执行器高性能的力控需求。

图7 -40%参数不匹配下力跟踪性能对比Fig.7 Comparison of force tracking performance under -40% parameter mismatch

图8给出了在GA从-90%到+70%不同参数的不匹配程度ψ下，3个控制器的力跟踪性能相对误差百分比力超调量F，力跟踪误差ΔF。INDI在±50%条件内表现出相同的性能，力跟踪误差不超过6%。即使是参数不匹配达到了-90%和+70%，力跟踪误差也不超过8%，表现出优秀的跟踪性能。在参数不匹配小于+50%(也就是处于理论分析的稳定域内)，INDI几乎没有超调，表现出较强的稳定性。在参数不匹配大于+50%，INDI表现出一定的超调现象，但幅度不大。相比之下，PID和NDI的跟踪误差随着不匹配水平的增加迅速从10%上升到30%，力超调最大达到了50%，表明在极度参数不匹配情况下，系统已经失去稳定性。由此，表明INDI对参数不确定性具有极强的鲁棒性。

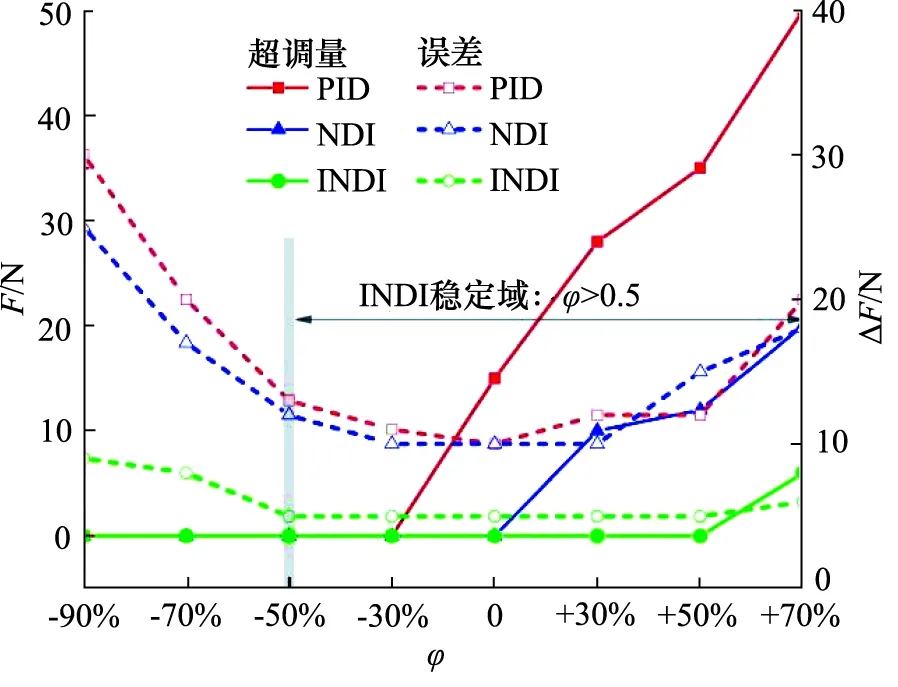
图8 不同参数的不匹配程度下相对性能对比Fig.8 Relative performance comparison for different parameters with different degrees of mismatch

当采样速率降低时，INDI控制性能随之会下降，如图9所示。当采样频率低于2000 HZ时，控制性能极差，而在10000 Hz频率下，INDI控制器存在较小的稳态误差。这一结果说明了INDI线性化的有效性依赖于高采样频率的假设。因此在实际中，控制器硬件条件允许情况下尽可能提高采样速率。

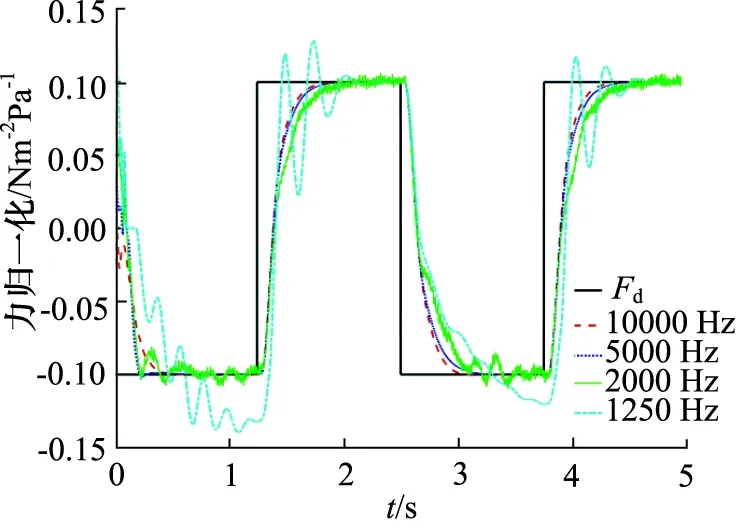
图9 不同采样速率下INDI控制性能对比Fig.9 Performance comparison of INDI at varies sampling rates

5 结论

(1) 与传统的反馈线性化方法NDI相比，INDI方法仅需要更少的模型信息却能提供更好的性能，因此非常适用于液压驱动的非线性、时变性和参数不确定极强的系统；

(2) 仿真表明了INDI对参数不确定的非线性模型的鲁棒性，力跟踪误差始终稳定在在6%左右，最大跟踪误差也不超过8%，验证了INDI稳定性的必要条件:模型的不匹配程度φ>0.5；

(3) INDI采用高频率滤波处理噪声，系统抗干扰能力增强，进一步验证了鲁棒性。