一种耦合电感增压直流变换器及其磁集成研究*

李洪珠 荆泽宇

(辽宁工程技术大学电气与控制工程学院 葫芦岛 125105)

1 引言

近年来，随着传统化石能源的不断减少，促使我们使用太阳能等新兴能源。由于太阳能光伏发电系统的直流输出电压远低于电网电压，因此，使用增压直流变换器势在必行[1-3]。DC-DC变换器中非隔离型变换器具有功率密度高，只使用一个开关管等优势[4-5]，因而得到了普遍研究。

目前，为达到直流变换器增压的目的，学者们提出了各种方案，文献[6-7]在传统变换器基础上引入开关电感和开关电容，但提出的变换器所使用二极管和开关管等器件数量较多，增大了变换器的器件损耗和开关管控制难度。文献[8]在前人的基础上运用耦合电感技术，使得变换器升高电压且减小了器件损耗，但由于漏感问题，开关管会有较大的电压尖峰。文献[9]增加无源箝位单元来吸收漏感能量，但是容易引起输入电流的不连续问题。由于传统的Sepic变换器输入电流连续，且因其有输入电感，因此可以减弱电路的EMI效应，且有输入输出同相的优势，因而得到了广泛应用。文献[10]将传统Sepic变换器与升压单元结合，但是所升高的电压非常有限。文献[11]将传统Sepic变换器和Boost变换器进行组合，但组合变换器的开关管电压应力较高，与输出电压相等。本文将文献[12]中提出的电容-耦合电感-电容(Capacitance-coupled inductor-capacitance，CLC)倍压单元引入传统Sepic变换器，进而提出一种新型耦合电感增压的Sepic变换器，该变换器实现了在升高电压的同时极大地降低了开关管电压应力。

所谓磁集成技术，是利用电力电子变换器中各磁性元件的磁通分布特点以及各绕组间的磁通耦合关系，将多个分立磁件从结构上集中在一个磁心上，从而达到减少元件数量，减小变换器体积和重量，提高变换器功率密度的目的[13-14]。本文提出一种新型4-U型磁心结构，与传统的E-E型磁心结构相比，磁通密度分布效果更好，同时集成磁件体积大大 减小。

2 变换器工作原理分析

2.1 拓扑结构

提出的CLC耦合电感增压的Sepic变换器拓扑如图1a所示，其中CLC耦合电感倍压单元是由耦合电感的副边与电容C3、C4和二极管D2、D3构成。对耦合电感进行等效变换后的等效电路如图1b 所示。

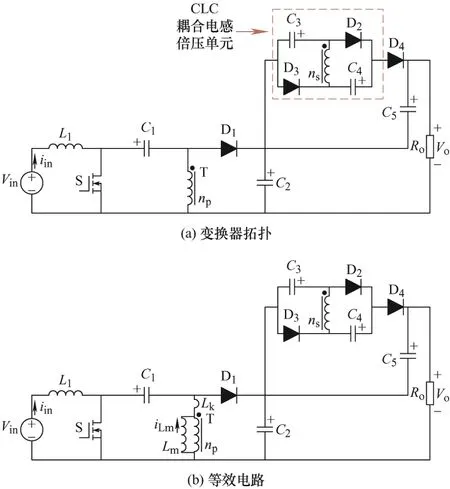
图1 CLC耦合电感增压的Sepic变换器拓扑

为简化分析，作出如下假设。

(1) 开关管和二极管均为理想器件。

(2) 电容的电容值足够大，其端电压保持 恒定。

2.2 工作模式分析

在电感电流连续工作(Continuous conduction mode，CCM)时，一个工作周期内，变换器有5个工作模式，等效电路如图2所示，主要工作波形如图3所示。

(1) 工作模式1：如图2a所示，L1储能，耦合电感T原边励磁电感Lm和漏感Lk储能。副边绕组和C3、C4串联给C5充电的同时与C2串联给负载供电。在t1时刻，此工作模式结束。在此阶段，iL1和iLm可以表示为

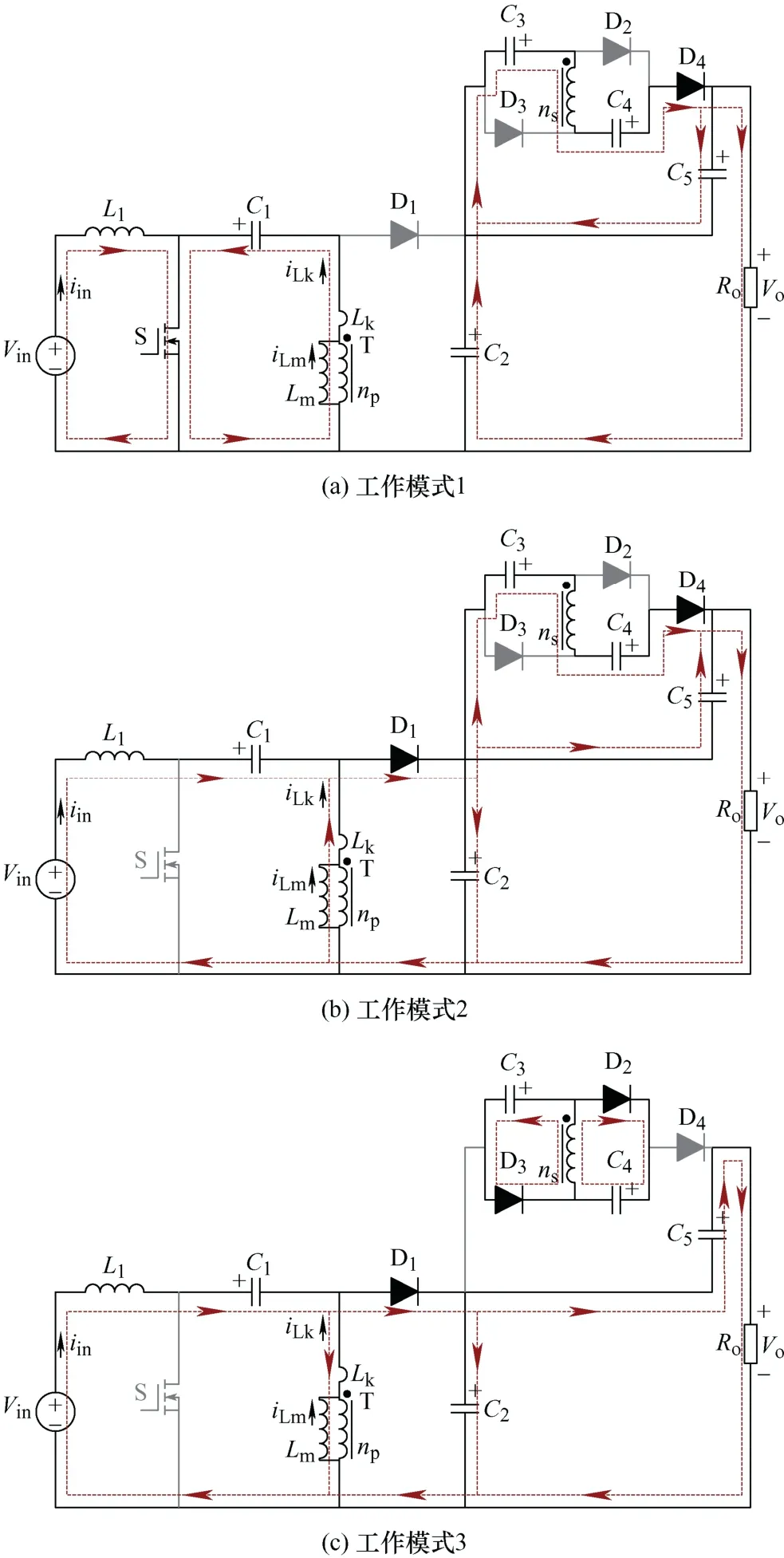
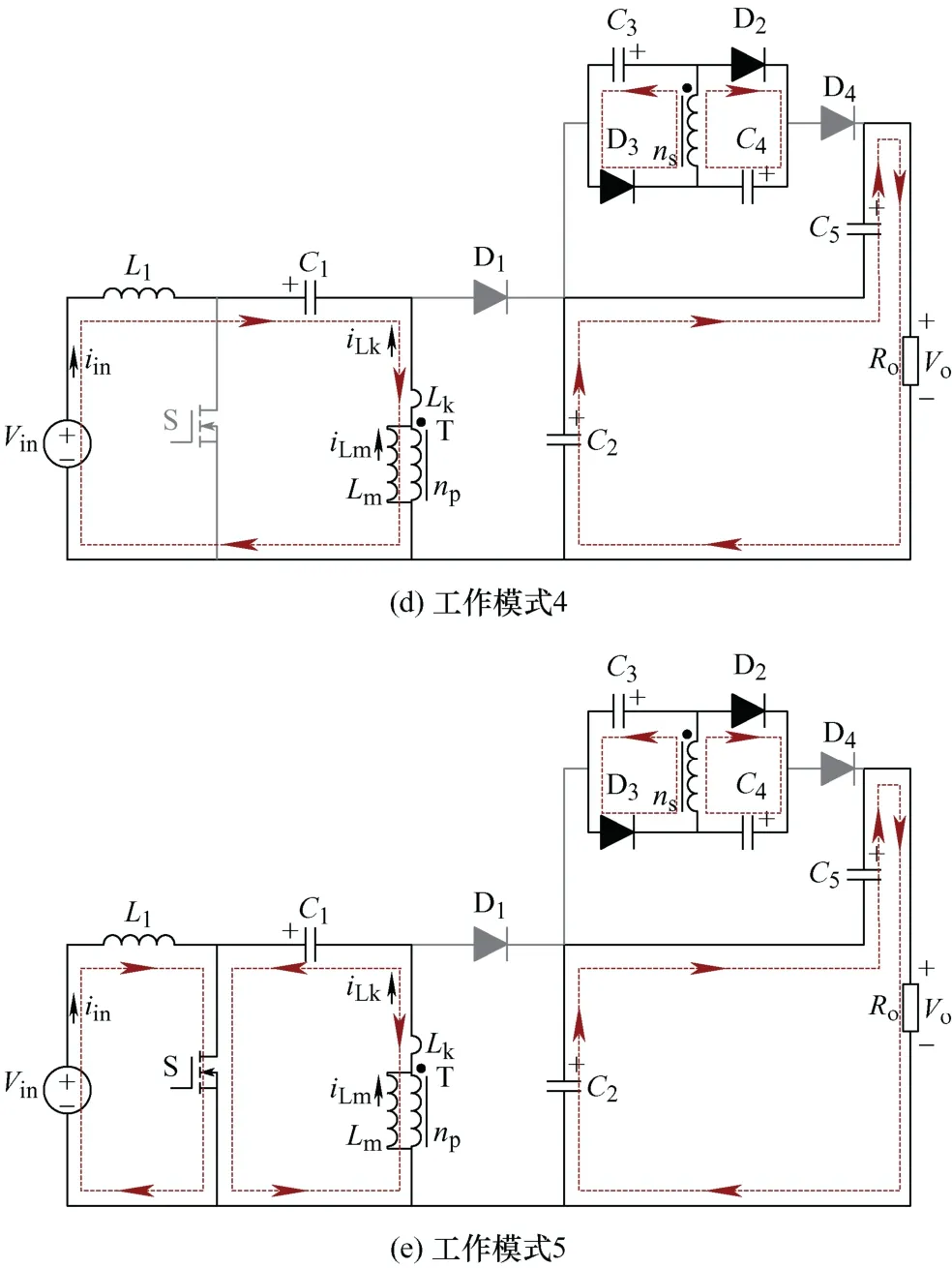
图2 各工作模式等效电路

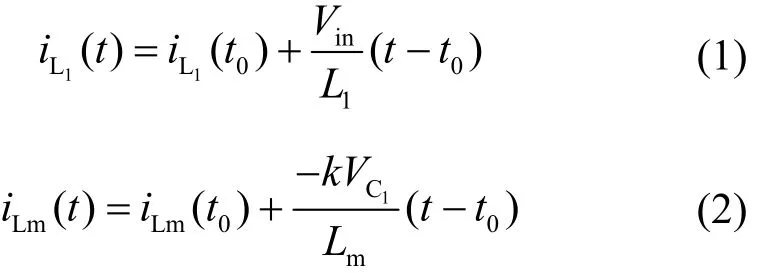
式中，k为耦合电感的耦合系数，为

(2) 工作模式2：如图2b所示，t1时刻，开关管S关断。漏感Lk与电源Vin和L1并联经D1给C1、C2充电并与C5串联给负载供电，Lm通过耦合电感T释放能量，副边绕组和C3、C4串联后与C5并联共同给负载供电。由于此工作模式过程极短，可认为励磁电感电流基本不变。在t2时刻，此工作模式结束。

(3) 工作模式3：如图2c所示，t2时刻，C1和C2继续充电，电源Vin、L1和C5继续给负载供电，同时通过耦合电感T的副边绕组分别给C3、C4充电。在t3时刻，此工作模式结束。在此阶段，iL1和iLm可以表示为

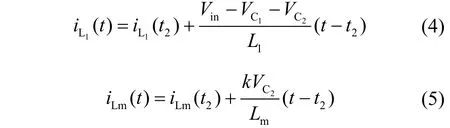
(4) 工作模式4：如图2d所示，t3时刻。电源Vin和L1给C1充电并通过耦合电感T的副边绕组继续分别给C3、C4充电。电容C2和C5串联放电。在t4时刻，此工作模式结束。

(5) 工作模式5：如图2e所示，t4时刻，开关管S导通。L1储能，C1放电，C3、C4充电。C2和C5继续串联放电。在t5时刻，二极管D4导通，此工作模式结束，进入下一个工作周期。

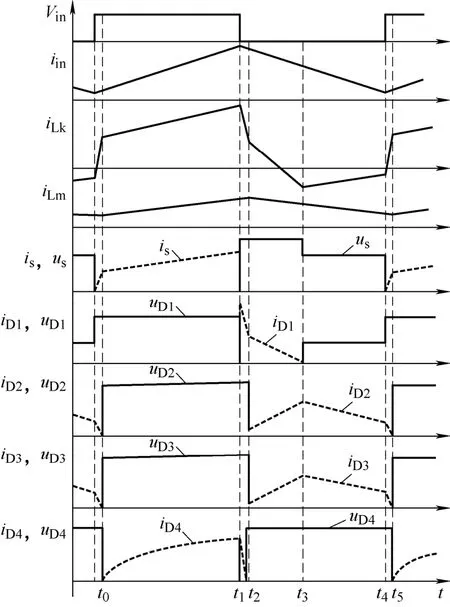
图3 变换器的主要波形图(CCM)

3 变换器稳态性能分析

3.1 电压增益及电压应力分析

在电感电流连续工作(CCM)时，为了便于稳态分析，忽略过渡工作模式2和5，仅讨论分析工作模式1、工作模式3和工作模式4。设耦合电感的匝比n为

当变换器在工作模式1时，根据图2a，有如下电压方程

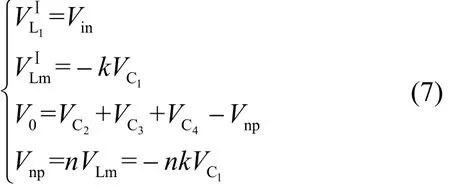
式中，Vnp为耦合电感的原边电压。

当变换器在工作模式3时，根据图2c，有如下电压方程

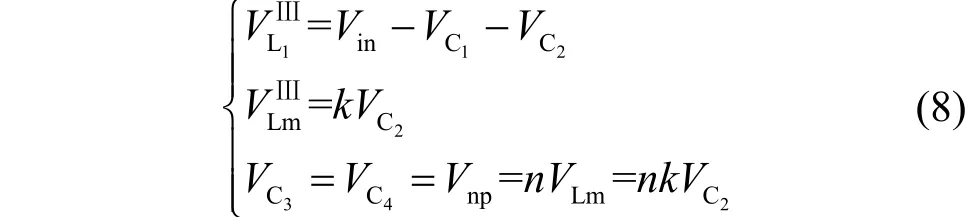
由电感L1和Lm的伏秒平衡原理可得

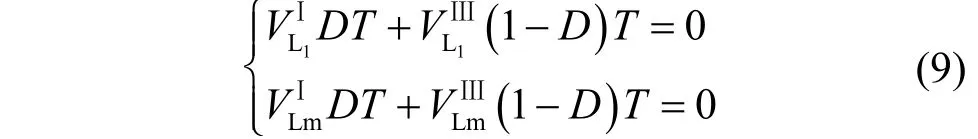
式中，D为占空比。

将式(3)、(6)～(8)代入式(9)可得输出电压Vo的表达式为

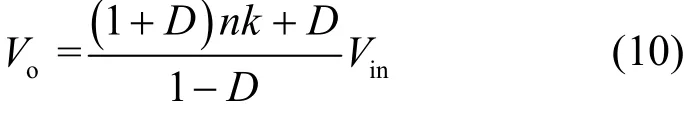
根据式(10)可以得到，在CCM时，变换器电压增益为

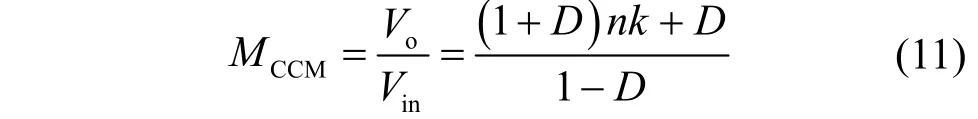
根据式(11)，MCCM与k、n以及D有关。关系曲线如图4所示。由图4可知，在D相同的条件下，当n不变时，k越大，变换器的电压增益越高。当k不变时，n越大，变换器的电压增益越高。

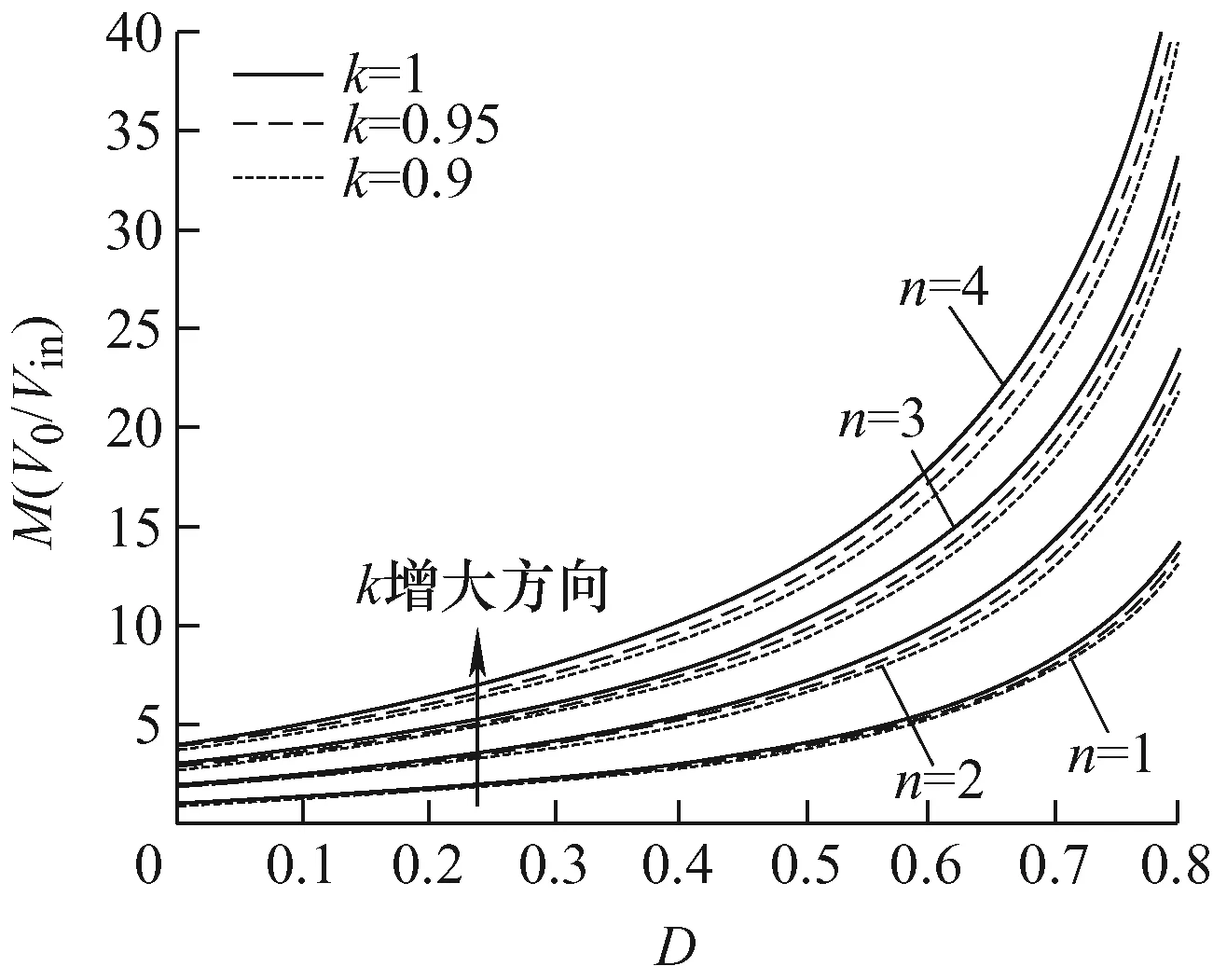
图4 变换器电压增益与k和n的关系曲线

为了便于简化分析，假设k为1，即忽略漏感Lk的影响。此时变换器的电压增益为

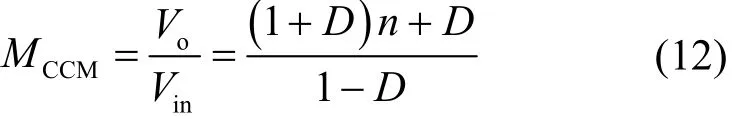
开关管S的电压应力

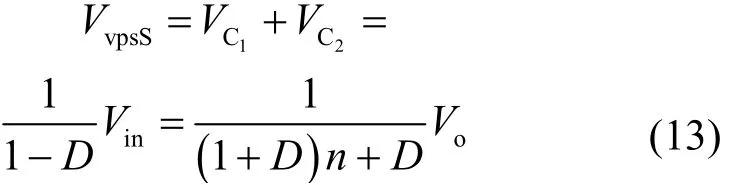
二极管D1～D4的电压应力为

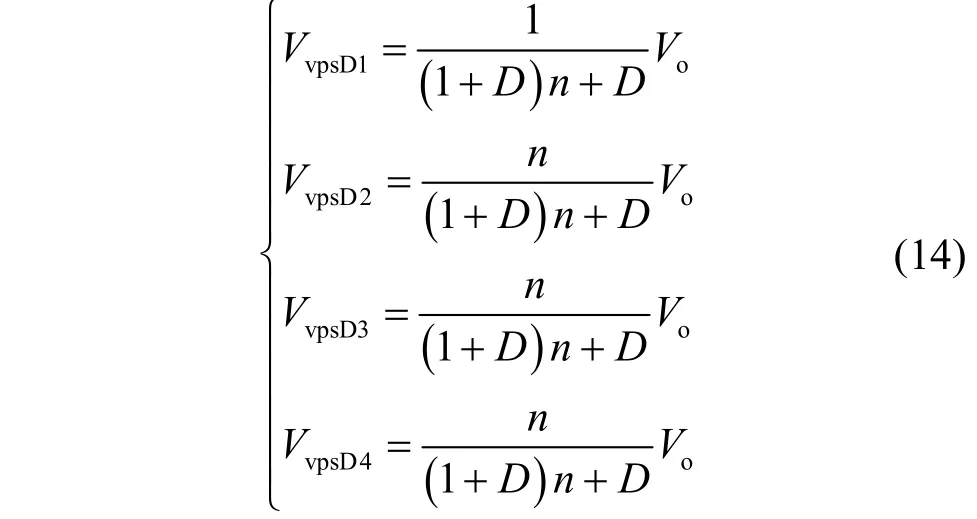
根据式(13)和式(14)，VvpsS和VvpsD1相同，VvpsD2、VvpsD3和VvpsD4相同。在实际应用过程中，应依据变换器的工作需求，合理选择各器件的型号。

3.2 临界等效电感时间常数分析

在电感电流断续工作(Discontinuous conduction mode，DCM)时，变换器的主要工作波形如图5所示。设D1T为二极管电流iD1从峰值降到零的时间，D2T为励磁电感电流iLm从峰值降到断续的时间。变换器在DCM模式的稳态分析类同于在CCM模式的稳态分析，此处直接给出变换器在DCM时，电压增益表达式如下

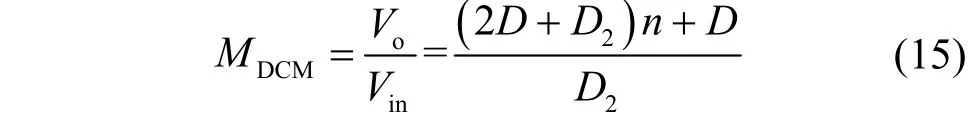
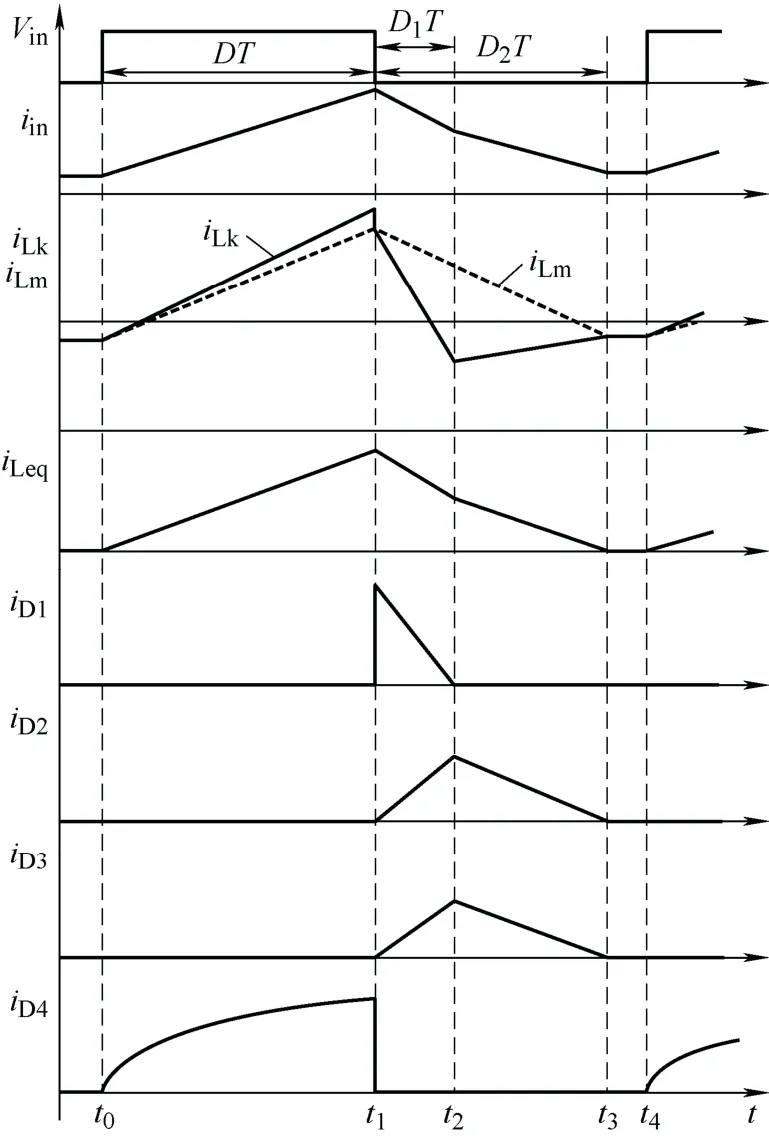
图5 变换器的主要波形图(DCM)

设iLeq为iLm和iin之和，其峰值为

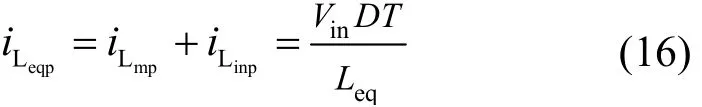
式中，Leq为变换器的等效电感，为

由电容的安秒平衡原理可得，在一个周期T内，电容C1～C5的平均电流为零，由此可得，所有二极管的平均电流等于输出电流Io。其中，二极管D1和D2的平均电流为

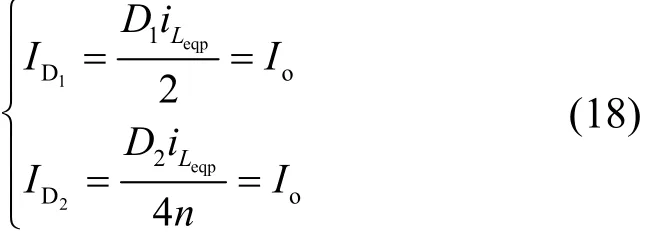
设等效电感时间常数 eqLτ为

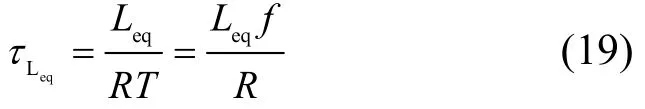
联立式(15)～(19)可得，变换器在DCM时，电压增益为

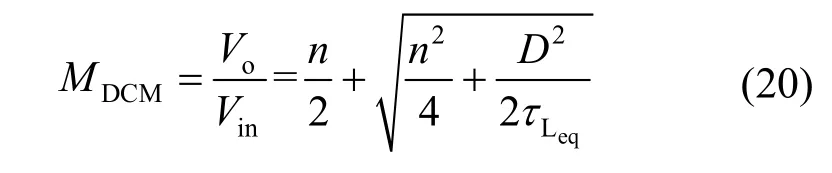
当MCCM与MDCM相等时，变换器工作在临界状态，可以求得临界等效电感时间常数为

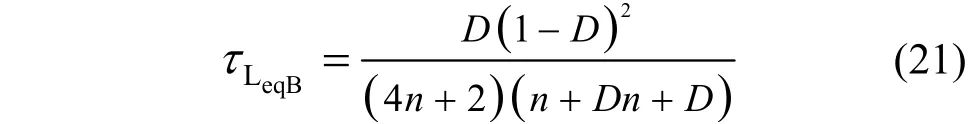
取n为2，τeqBL与D的关系曲线如图6所示。由图6可知，当 eqLτ大于 eqBLτ时，变换器工作在CCM模式；当τeqL小于τeqBL时，变换器工作在DCM模式。在D取0.5时，τeqBL为0.003 57。

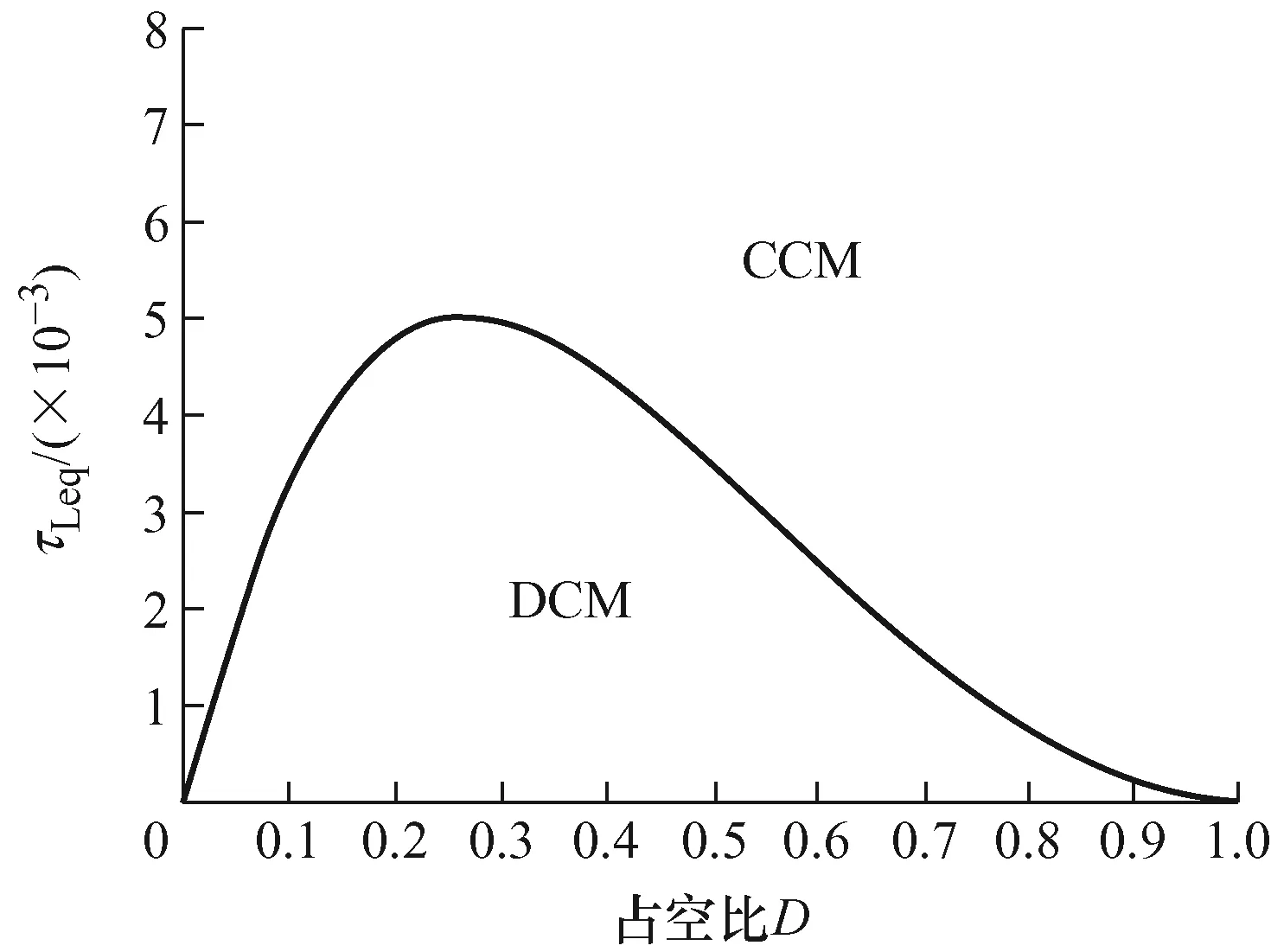
图6 τeqBL 与D的关系曲线图

利用临界等效电感时间常数可以设计电感L1的参数。临界状态的电感L1B为

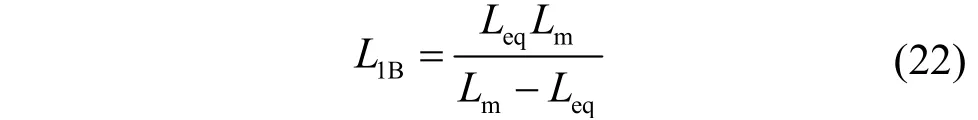
在实际应用过程中，应使得电感L1大于L1B，使变换器工作在CCM模式。

3.3 变换器性能对比

将本文所提变换器与传统Sepic变换器、文 献[10-11]的变换器做对比，参数对比情况如表1所示。取n为2，D为0.5时，与传统Sepic变换器相比，本文提出的变换器升高了近7倍电压增益，与此同时，开关管的电压应力也降低了近7倍。

表1 不同变换器性能参数

当n=2时，各变换器的增益对比曲线如图7所示。可以看出，本文提出的变换器的电压增益在D小于0.8范围内明显更高于其他Sepic变换器。虽然在D大于0.8时文献[10]的电压增益更高，但是属于极限占空比情况，不符合实际应用。变换器的开关管电压应力对比曲线如图8所示，可以看出，在D大于0.45时本文提出的变换器开关管的电压应力更小，虽然在D小于0.45时文献[11]的开关管电压应力略小一点，但是占空比无法符合实际情况。综上所述，在有效占空比为0.45～0.8范围内，本文提出的变换器总体性能更好。

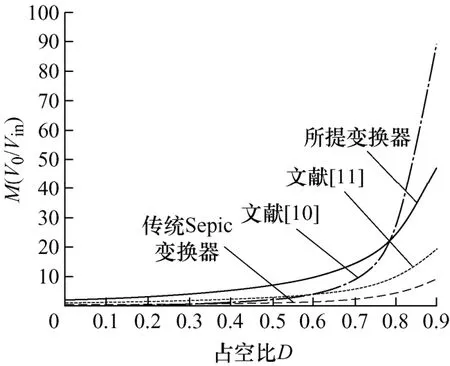
图7 变换器增益对比曲线

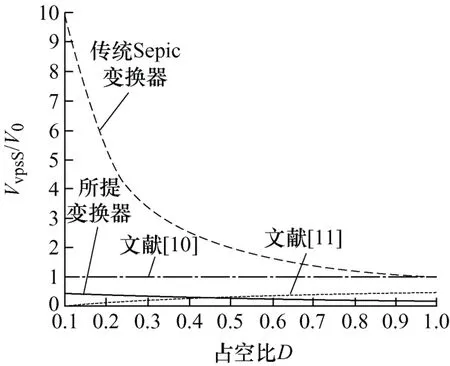
图8 变换器开关管电压应力对比曲线

4 集成磁件设计

本设计试验样机的输入电压为12 V，输出电压为84 V，额定功率Po为60 W，取耦合电感匝比n为2，占空比D为0.5时，由式(17)、式(19)、式(21)和式(22)可以得出励磁电感Lm可取50 μH，电感L1取20 μH。

4.1 磁心结构

在传统解耦磁集成使用的E-E型磁心的启发下，提出4-U型磁心结构如图9所示，将变换器中的耦合电感绕制在磁心中柱上，使得耦合电感的原边线圈和副边线圈反向耦合。与传统的E-E型磁心相比，本文提出4-U型磁心结构具有如下优点：磁心体积减小，磁通密度分布更加均匀。

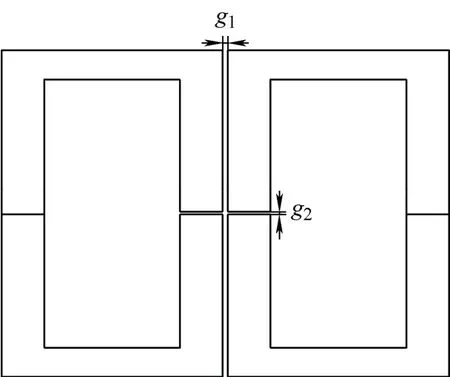
图9 4-U型磁心结构

耦合电感的参数值如表2所示。本设计的最大磁通密度Bmax取0.3 T，计算的AP值为0.227 cm4。根据磁心手册可知，额定功率为50 W所对应的磁心型号为EE28，提出4-U型磁心结构中单个U型磁心型号为UU16。相应的磁心设计如表2所示。

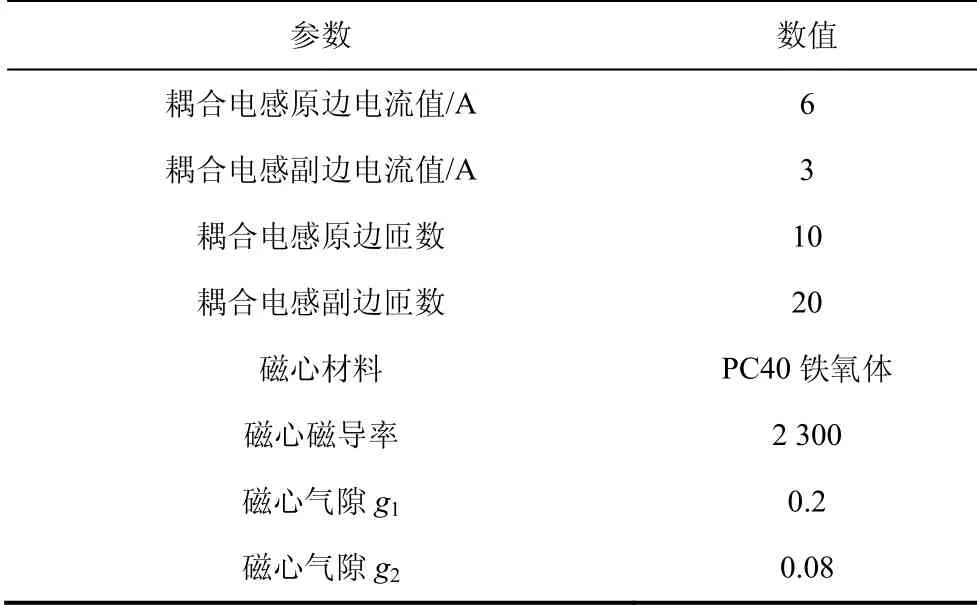
表2 耦合电感设计参数及磁心设计

耦合电感的线圈有以下三种绕线方式。

方案一：在磁心整个中柱上先绕制耦合电感的原边线圈；原边线圈绕线完成后在此基础上绕制耦合电感的副边线圈。

方案二：在磁心中柱的上面部分先绕制耦合电感的原边线圈；然后在磁心中柱的下面部分再绕制耦合电感的副边线圈。

方案三：在磁心中柱上先绕制一匝耦合电感的原边线圈，再绕制两匝耦合电感的副边线圈，然后再绕制一匝耦合电感的原边线圈，以此类推，直至绕线完成。

运用Maxwell仿真软件对三种绕线方式的4-U型磁心进行有限元仿真对比，磁通密度对比结果如图10所示，可以看出，方案三的最大磁通密度远大于磁心饱和磁通密度0.3 T，所以不适用于本设计，方案一与方案二相比，最大磁通密度更小，所以采用方案一。

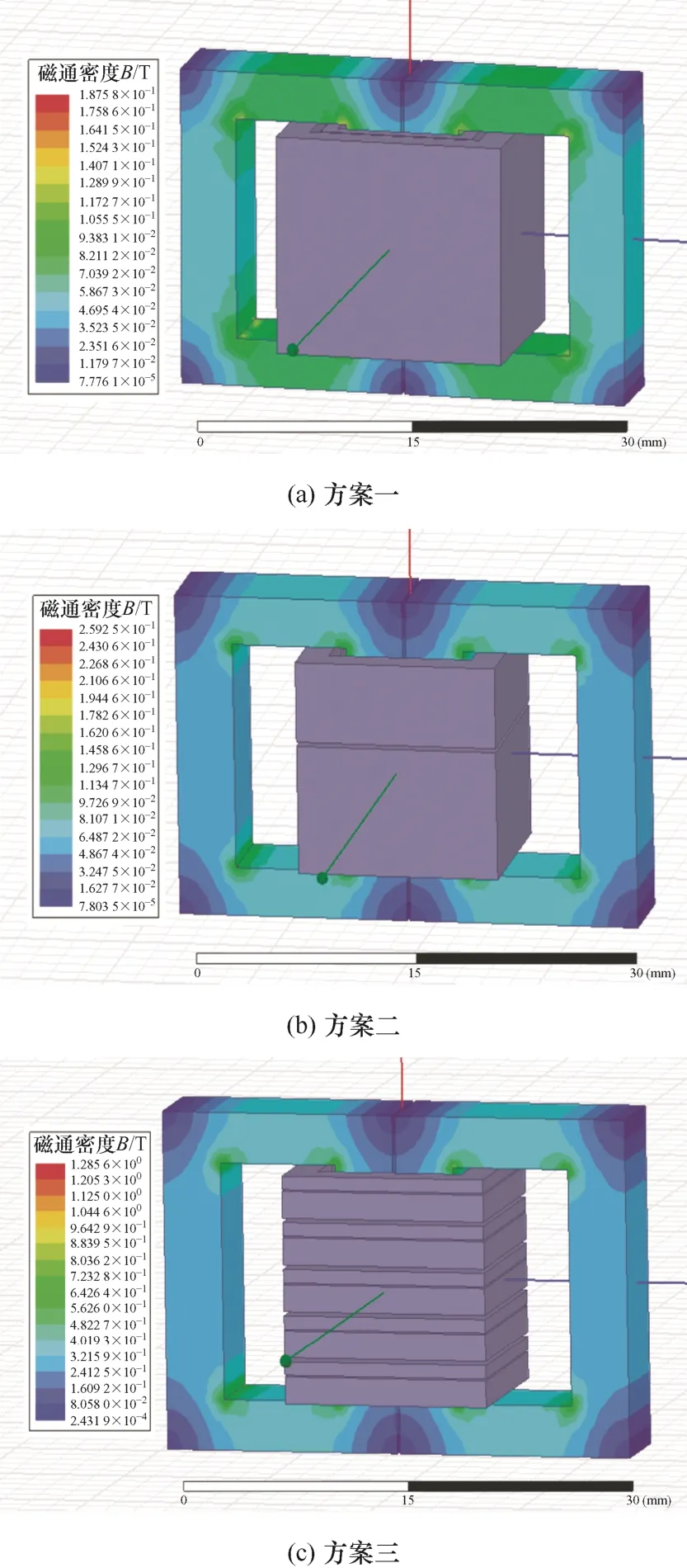
图10 绕线方式

E-E型磁心磁通密度分布如图11所示，与图10a的4-U型磁心相比，可以明显看出，在相同的绕线方式下，E-E型磁心的最大磁通密度大于4-U型磁心的最大磁通密度，且4-U型磁心的磁通密度分布更加均匀，磁心的利用率更高。所以使用提出的新型4-U型磁心结构更好。

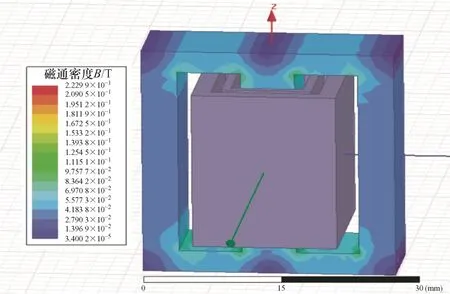
图11 E-E型磁心磁通密度分布

4.2 解耦磁集成设计

为了进一步减小拓扑结构中的磁性元件的体积，本文运用抵消耦合作用的解耦磁集成方法，将拓扑结构中的电感L1与耦合电感进行磁集成，将电感L1绕制在4-U型磁心的两个边柱上，电感L1的激励电流值为5 A。

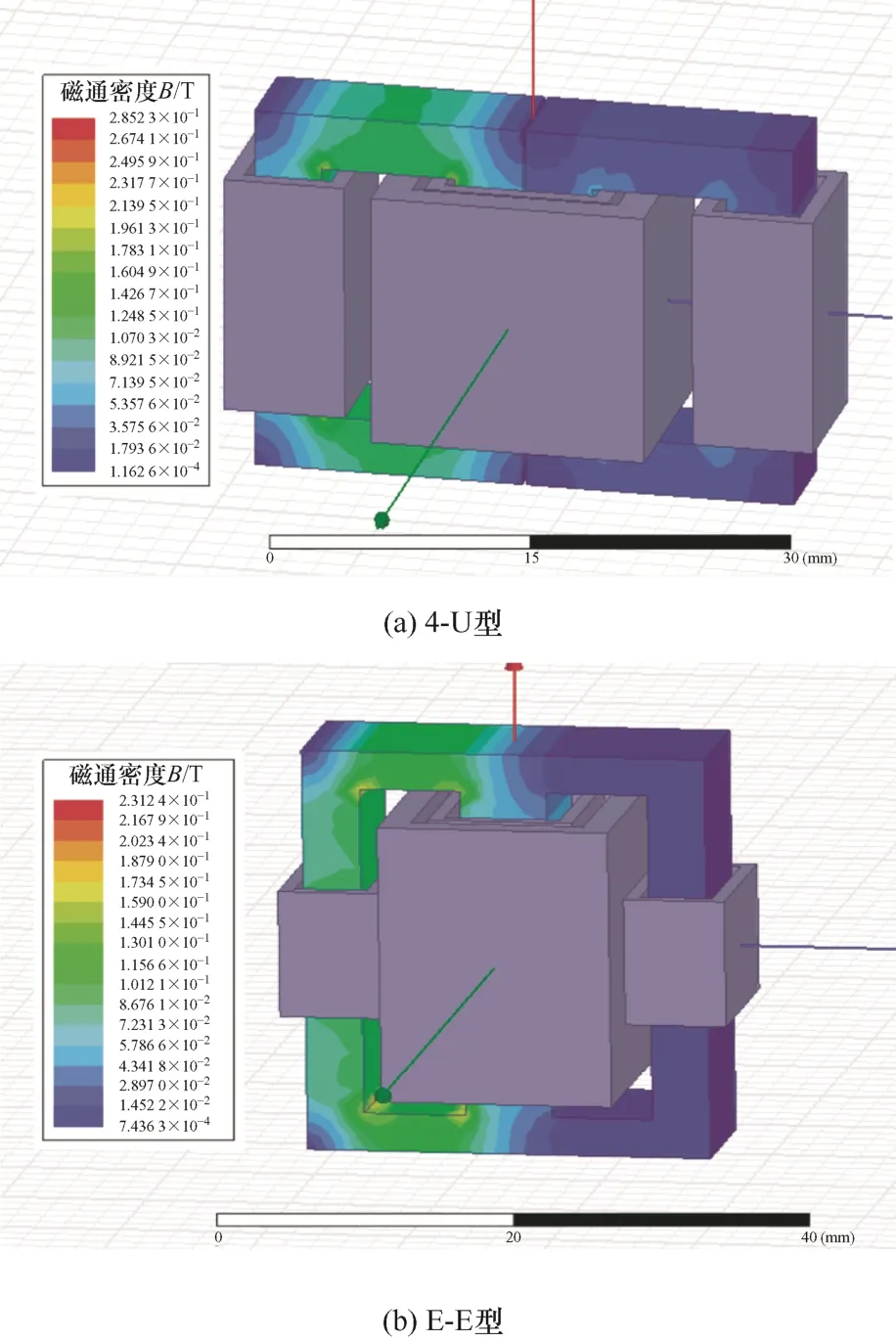
图12 集成磁件磁通密度分布

集成磁件磁通密度分布如图12所示，可以看出，两种磁心的最大磁通密度均小于磁心饱和磁通 密度0.3 T，磁心均未出现饱和现象，表明集成磁件设计的合理性。但是，4-U型磁心的最大磁通密度小于传统E-E型磁心的最大磁通密度，说明在相同电感参数下，4-U型磁心的利用率更高。温度场仿真结果如图13所示，可以看出，4-U型集成磁件的散热效果更加均匀。与E-E型磁心的集成磁件实物对比结果如图14所示，可以看出，4-U型磁心的磁件体积明显小于传统E-E型磁心的磁件的体积。综上所述，本文所提4-U型磁心的整体性能优于传统的E-E型磁心。

图13 温度场仿真

图14 实物对比图

5 试验

试验样机的主电路参数如表3所示。试验样机的Vo、Vin和VS波形如图15所示，可以看出，该变换器实现了输入12 V，输出84 V的升压变换，且变换器的开关管电压应力约为24 V，约为输出电压的0.28倍，因此开关管的电压应力较低。二极管的电压波形如图16所示，其中，二极管D1的电压应力约为24 V，二极管D2、D3、D4的电压应力约为45 V，均符合前面的理论分析。在输出电压为84 V的情况下，二极管的电压应力也较低。

表3 主电路参数

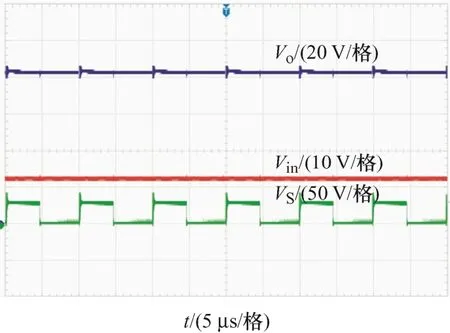
图15 Vin、Vo、VS波形图

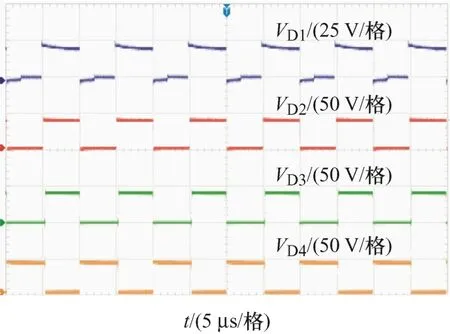
图16 VD1、VD2、VD3、VD4波形图

试验样机的电流波形如图17、18所示，可以看出，以上电流波形均符合前文理论。效率曲线如图19所示，可以看出，在输出功率为45 W时，效率最高，为93.9%。

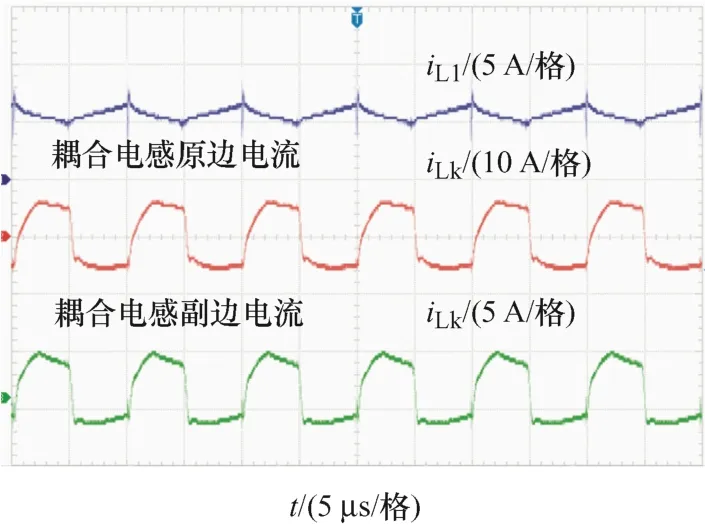
图17 iL1、iLk波形图

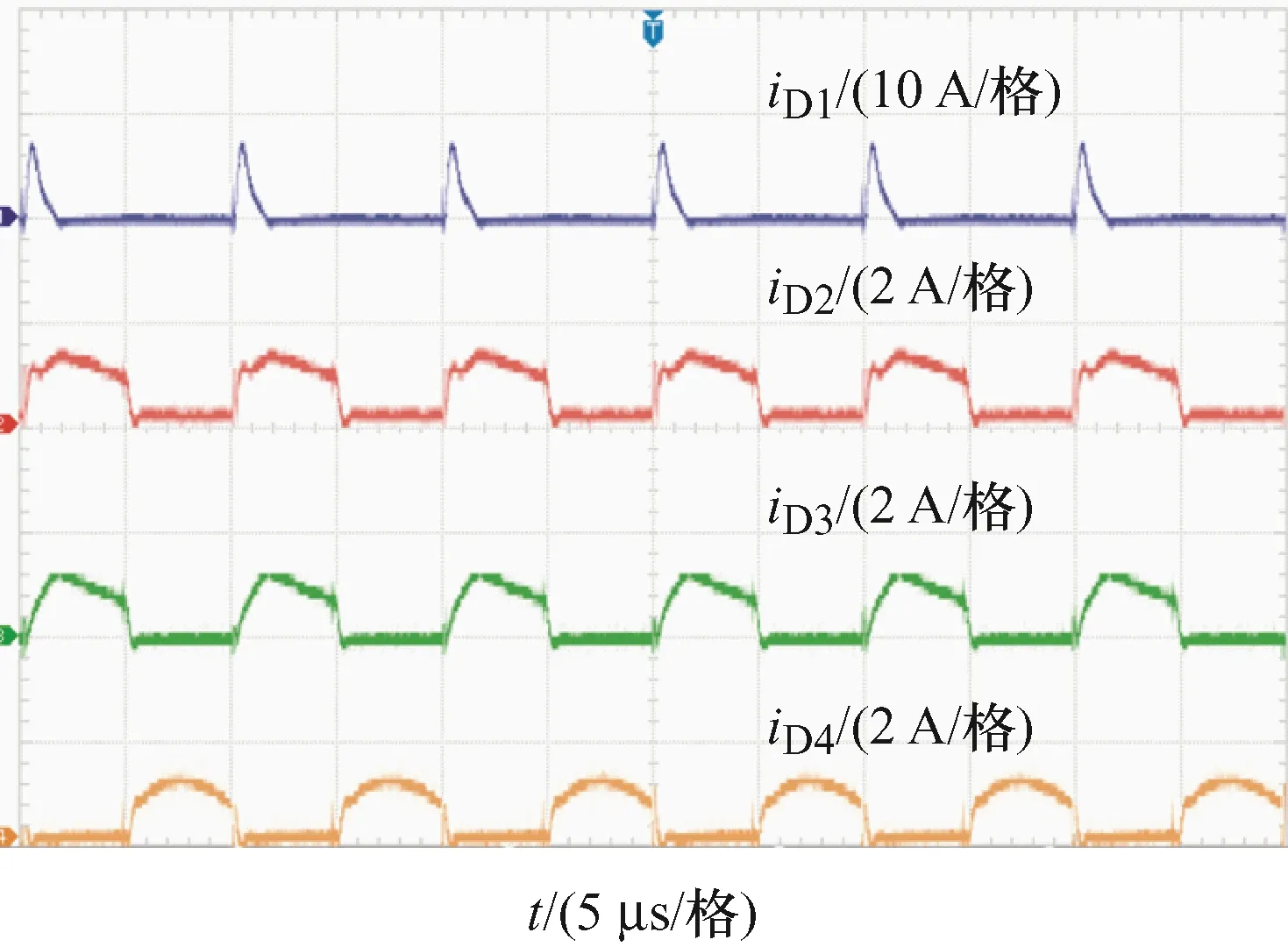
图18 iD1、iD2、iD3、iD4波形图

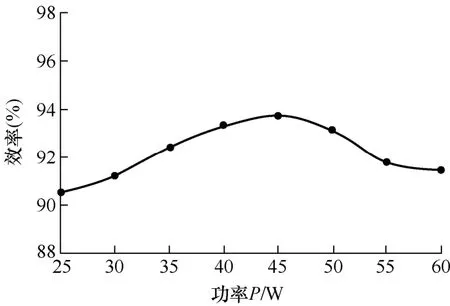
图19 效率曲线

6 结论

为了提高光伏发电的输出电压，本文以传统Sepic变换器为基础，引入CLC倍压单元，从而提出一种新型增压Sepic变换器拓扑结构，并推导出其电压增益及电压应力表达式和临界等效电感时间常数。为了进一步减小该拓扑结构中磁性元件的体积，本文提出新型磁心结构，运用解耦磁集成的方法，将拓扑结构中的磁性元件进行磁集成，得到结论如下。

(1) 临界等效电感时间常数只与占空比有关，可利用该时间常数设计输入电感参数。

(2) 通过与其他的Sepic变换器相比，在相同占空比下，本文所提的基于CLC倍压单元增压的变换器在升高了近7倍电压增益的同时极大降低了开关管的电压应力。

(3) 与传统解耦磁集成使用的E-E型磁心结构相比，新型4-U型磁心结构的磁通密度分布更加均匀，磁心利用率更高；进行解耦磁集成后得到的拓扑结构中的磁性元件体积更小，散热性能也更好。