斜拉桥模态测试与试验技术研究

卢旭阳，周关艺，宋小金

（1.湖南华城检测技术有限公司，湖南 长沙 410205；2.中大检测（湖南）股份有限公司，湖南 长沙 410213）

引言

在桥梁跨径范围300～1000 m 之间，斜拉桥有较为明显的经济优势。斜拉桥作为一种拉索体系，比梁式桥的跨越能力更大，是大跨度桥梁的最主要型式［1］。对于新建桥梁，尤其是大跨度桥梁，通过现场静动载试验，可以评定桥梁设计施工质量，确定桥梁工程的可靠性，检验校核和进一步完善桥梁设计基础理论。桥梁结构自振特性试验是大跨径斜拉桥动载试验的主要内容之一［2］。

1 脉动测试

随着计算机与信号技术的飞速发展，对实际结构进行脉动试验，即利用环境激励获得在小的激励下结构物的动力特性是可行的［3］。由于结构的模态参数是结构固有特性，可以从分析信号中剔除无关的噪声，正确地识别结构的模态参数，这在大跨度柔性结构斜拉桥的识别方法中效果很好［4］。

脉动法也称为环境激励法，特别适合柔性结构整体的自振特性。试验通过超低频加速度传感器拾取大桥各测量部位的环境振动响应。由于大桥跨径大而设备数目有限，测试时设定某一点为参考点。该传感器位置固定，通过多次移动其他传感器位置得到全桥的振动响应［5］。先将各测点获得的环境振动数据通过滤波除去高、低频信号成分，然后对滤波后的数据进行自功率谱和互功率谱分析。自功率谱密度与相关函数用来确定各模态的频率，互功率谱密度与相位差函数用来确定各模态的振型［6］。

2 斜拉桥动力特性

2.1 动力特性分析理论

在动力学问题中，体积的等效节点力：

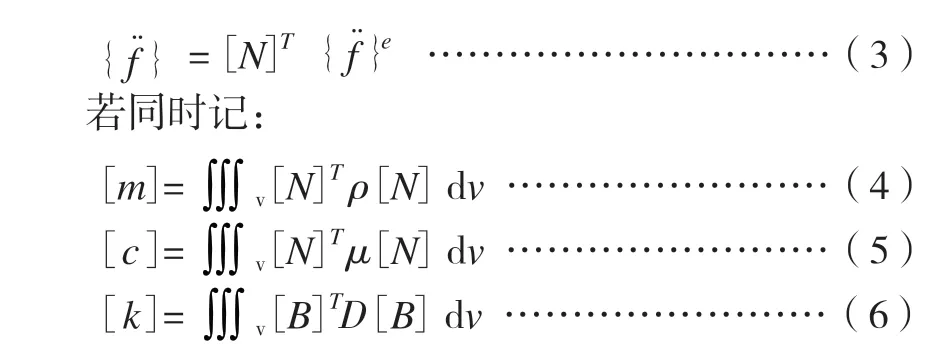
式中：［m］、［c］、［k］—单元的质量矩阵、阻尼矩阵、刚度矩阵；B、D—单元的应变矩阵与弹性矩阵。

则公式（1）可变：

将所有的单元动力平衡方程式集合起来，可以得到结构的自由振动总体平衡方程：

在无外力作用时（｛F｝=0），由于阻尼对结构自振特性的影响很小，因此在求结构的自振频率和振型时通常忽略阻尼的影响（［c］=0），则公式（8）可以简化：

由公式（9）为二阶常系数线性齐次微分方程，其解的形式：

将公式（10）带入公式（9）可以得到公式（9）相对应的特征方程：

由于位移是任意的，则公式（10）应满足：

求解公式（12）的广义特征值即可。

子空间迭代法是求解大型复杂结构特征值问题的常用方法，该方法采用多个线性无关的向量同时迭代，只要选择合适的迭代精度就可以得到完全可靠的结果［7］。求解出满足公式（13）的前m 阶特征解：

式中：ωi——结构的m 阶自振频率，i=1，2，3，…，m；｛φm｝——结构的m 阶模态振型，｛φm｝=［φ1，φ2，φ3，…，φm］。

2.2 斜拉桥动力特性

斜拉桥进行动力特性分析时，首先进行恒载状态下的非线性静力分析，然后进行动力特性分析。由于空间斜拉索的存在，斜拉桥的侧向弯曲和扭转强烈耦合在一起，只有侧向弯曲为主兼有扭转的振型［8］。斜拉桥进行动力分析时须将荷载转化到“X、Y、Z”三维空间上。对于斜拉桥的模态振型来说，纵飘振型、对称竖弯振型及对称扭转振型三个模态振型相对关键，前两个振型是决定结构抗震性能的，后两个振型决定抗风分析的，这些是理论分析与现场测试的关键振型，传感器的布置需要应充分考虑。

运用子空间迭代法对桥梁结构进行动力特性分析。斜拉桥桥梁结构前9 阶自振频率与模态。

3 斜拉桥模态测试

3.1 工程概况

北江四桥分北引桥、主桥、南引桥。桥跨布置为北引桥3×30 m +3×30 m +4×50 m +4×50 m，主桥100 m +218 m +100 m，南引桥3×50 m +2×47 m +3×30 m+3×30 m +3×30 m。主桥采用塔梁固结，塔墩分离模式，全桥共48 对索。图1 为北江四桥主桥型布置。

图1 主桥桥型布置/m

3.2 试验内容

脉动试验通过采用高灵敏度的拾振器和放大器测量结构在环境激励下的振动，然后进行分析，求出结构自振特性。通过对拾振器拾取的响应信号进行频谱、模态等分析，可确定桥梁的自振频率。

（1）测试系统流程。速度（加速度传感器）→信号采集仪→信号采集分析处理软件系统。

（2）测点布置。在脉动试验中，传感器均为竖向拾振器，采集竖向振动速度信号，传感器布置见图2。

图2 主桥脉动试验传感器布置/m

（3）测试方法。将传感器置于测点上，由其拾取桥梁结构在大地脉动作用下的振动响应。

（4）理论分析。采用有限元分析软件建立该桥的有限元计算模型，经计算分析北江四桥主桥，模态见图3～图5。

图3 主桥二阶主梁竖向对称弯曲模态（f=0.984）

图4 主桥四阶主梁竖向弯曲/纵飘模态（f=2.168）

图5 主桥九阶主梁横向扭转模态（f=3.650）

3.3 试验结果

主桥模态试验结果见图6～图8，主桥理论频率与实测频率结果对比见表1，图9 为实测频率与理论值对比。

图6 第二阶实测频率（f=1.196）

图7 第四阶实测频率（f=2.295）

图8 第九阶实测频率（f=3.735）

图9 实测频率与理论值对比/Hz

表1 北江主桥频率测试结果与理论频率对比

从表1 及图9 中可以看出，各测工况脉动试验测试得到的该桥模态振动频率皆大于理论基频，表明该桥刚度满足设计要求。试验实测频率与计算频率的百分误差为2.3%～31.7%，从第三阶振型主梁竖向弯曲模态到第九阶主梁横向扭转模态实测频率与理论计算频率较为接近且相对误差＜10%，其中第八阶主塔纵飘模态与第九阶主梁横向扭转模态的差别最小。

4 结语

（1）介绍斜拉桥的动力特性及其理论分析，提出理论计算斜拉桥多阶自振模态可行性，引出先进行恒载状态下的非线性静力分析，再进行动力特性分析的方法。（2）工程实例试验结果表明频率实测值与理论接近，桥梁结构的自振特性理论计算与实际结构动态受力情况一致。桥梁结构振型的实测值与理论值比较可以得出，多阶振型之间的吻合性较好，即验证了模态分析方法的合理性，也表明有限元仿真软件计算出来的模型结果是比较准确的。（3）通过分析试验实测频率与计算频率的百分误差，大部分阶段桥梁结构频率计算值与实测值结果较为接近，可以说明使用环境随机振动法来识别固有模态参数是可行的。实测频率值略大于理论计算频率值，表明桥梁结构的刚度满足设计要求。