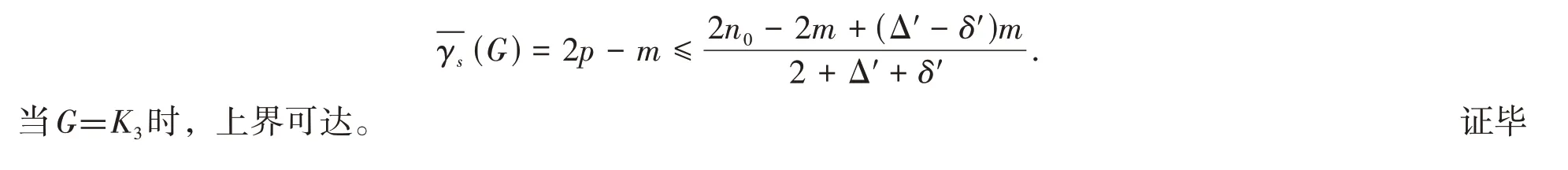图的反符号边控制数的新上界*

丁宗鹏

湖南第一师范学院数学与计算科学学院，湖南 长沙 410205

本文中所指的图均为无向简单图，顶点集为V，边集为E。没有说明的术语和符号参照文献［1］。设G=(V，E)为一个图，对于任意顶点v∈V，则NG(v)表示G中与v相邻的点集，称为v的邻域，NG[v]=NG(v) ∪{v}为v点在G中的闭邻域。dG(v) =| |NG(v) 表示v在G中的度。若一个图中每个顶点的度都为r，则称这个图为r正则图。NG(v)，NG[v]，dG(v)可分别简记为N(v)，N[v]，d(v). 记Δ 和δ分别为图G的最大度和最小度。

类似地，对任意边e∈E(G)，则NG(e) 表示G中与e相邻的边集，称为e的边邻域，NG[e]=NG(e) ∪{e}为e点在G中的闭边邻域。dG(e) =| |NG(e) 表示e在G中的边度，NG(e)，NG[e]，dG(e)可分别简记为N(e)，N[e]，d(e). 记Δ′和δ′分别为图G的最大度和最小度。

记图G=(V，E)的顶点数为n，边数为m. 若e=uv∈E，我们不难得到d(e)=d(u) +d(v) - 2，于是2δ- 2 ≤d(e)≤2Δ - 2，且有

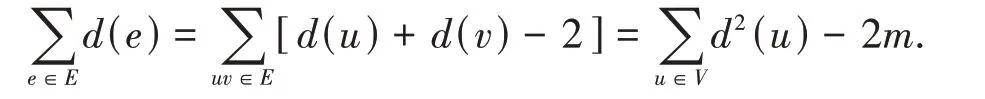
近年来，图的控制理论的研究日趋活跃，相继产生了各种控制概念。图的很多不同类型的控制概念及其变化形式被Cockayne 等［2］先后引入。Haynes 等［3-4］中阐述了目前所取得的主要研究成果。但是大多概念和结论都是围绕图的点控制展开，而图的边控制涉及不多。Xu在文献［5］中率先引入图的符号边控制概念，并在此基础上展开相关研究［6-7］。文献［8］定义了图的逆符号边控制，并研究了逆符号边控制数的上界。其他关于图控制数的相关结果可参考文献［9-13］。本文我们首先引入图的反符号边控制的定义，给出一般图的反符号边控制数的若干新上界，并且证明这些上界都是可达的。

1 反符号边控制数的概念及性质

问题的提出：将一个图的边集E划分为E1和E2，使得G中每条边的闭邻域中第一类边不多于第二类边，问这两类边的数目之差 |E1|-|E2|最多是多少？

2 反符号边控制数的新上界

为了方便，设R是一个实数集，且f：E→R是一个函数，S⊆E(G)，则记f(S) =. 并且，将f(N[e])记为f[e]. 用Pn表示具有n个顶点的一条路，用Kn表示具有n个顶点的完全图。

定理1 对于任意n阶连通图G，其边数为m，边度为奇数的边共n0条，则有

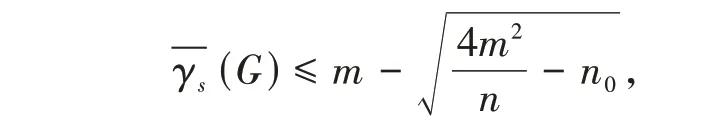
且此上界是可达的。

证明 设f为图G的一个最大的反符号边控制函数，且(G) =f(E).

令

P={e∈E|f(e) = 1} ,P0={e∈P|d(e)为奇数} ,Pe=P-P0;Q={e∈E|f(e) =-1},Q0={e∈Q|d(e)为奇数}，Qe=Q-Q0. |P|=p，|Q|=q，|P0|=p0，|Pe|=pe，|Q0|=q0，|Qe|=qe.依照图的反符号边控制的定义，对任意e∈E(G)，f[e]≤0. 于是有

因此

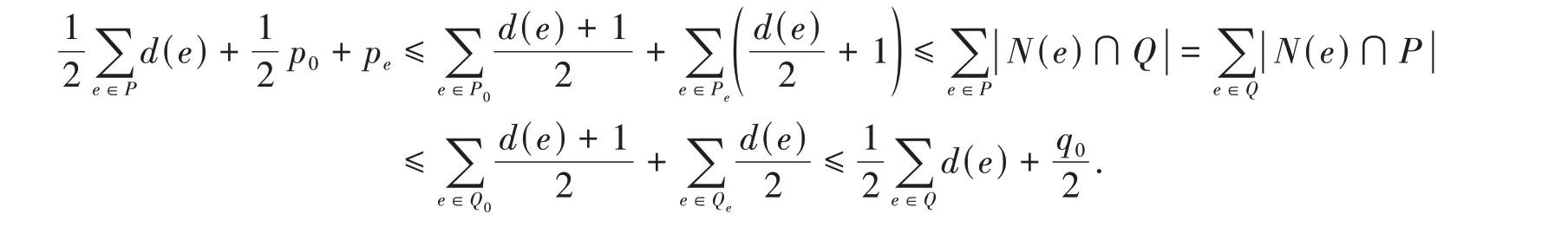
即

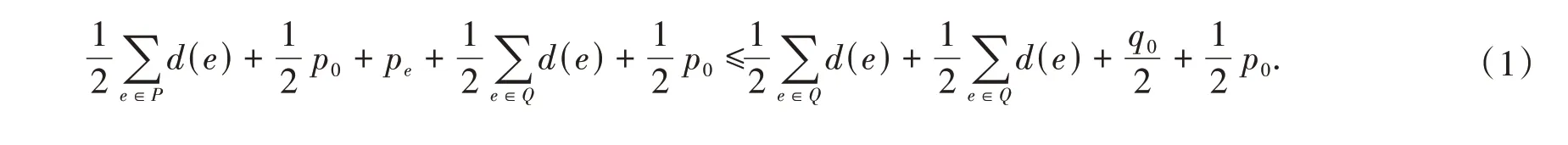
综合式（1）和式（2）得

注意到p=m-q，由式（3）得

综上所述得

定理2 对于任意n阶连通图G，其边数为m，Δ′，δ′分别是其最大边度与最小边度，边度为奇数的边共n0条，则有

且此上界是可达的。

证明 设f为图G的一个最大的反符号边控制函数，且(G) =f(E).

令

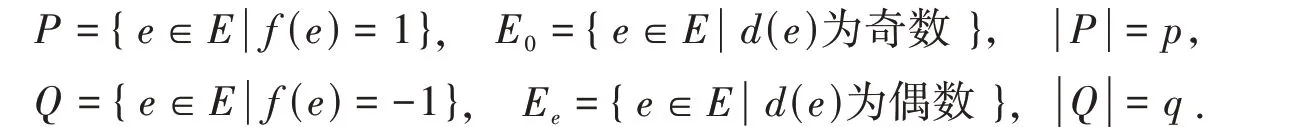
依定义知，对任意e∈E0，f[e]≤0；对任意e∈Ee，f[e]≤-1.于是有

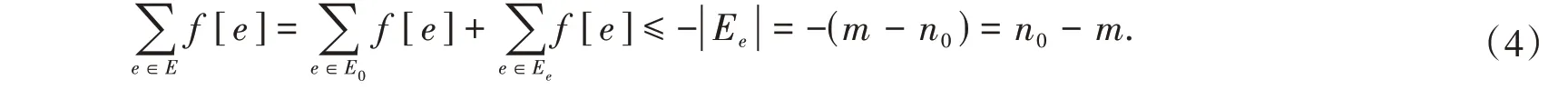
另外，

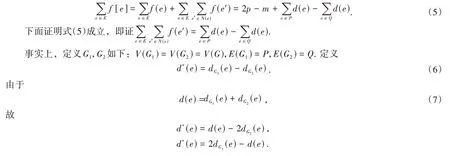
所以

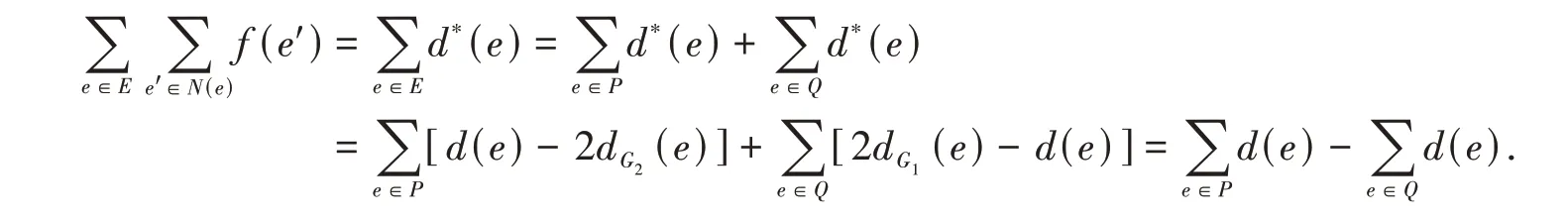
至此式（5）得证。

于是

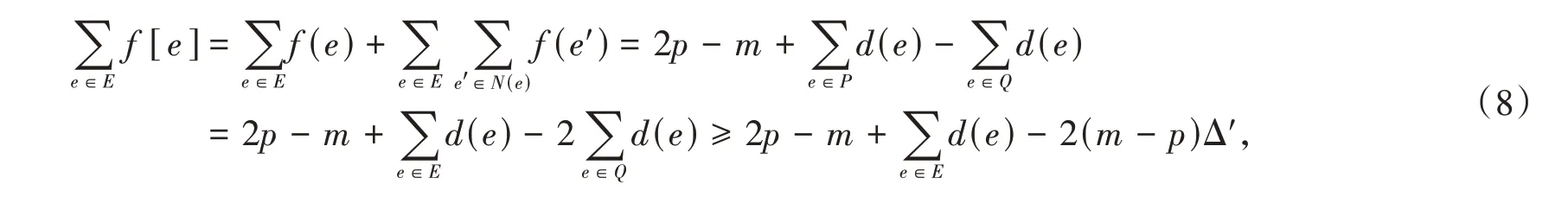
从而

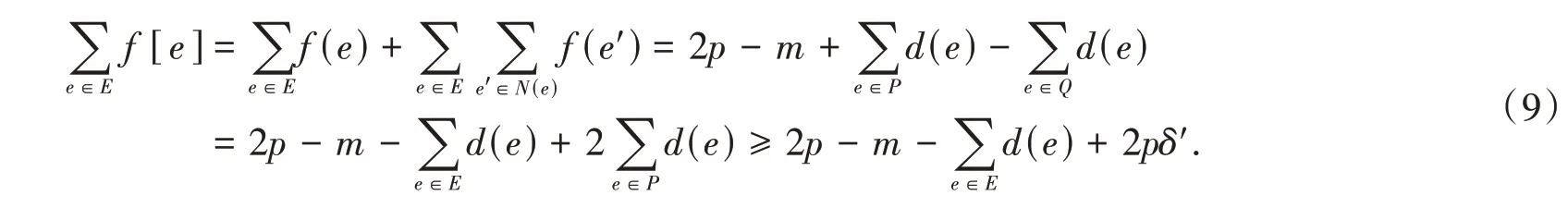
由式（4）和式（8）得

又由式（4）和式（9）得

综上可得

证明 由定理2的证明

可得

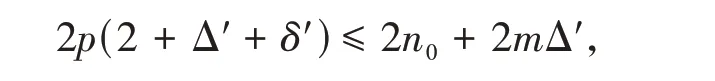
即

于是