基于惯性/激光测距/视觉里程计组合的高空场景尺度误差估计方法

王大元, 李 涛, 庄广琛, 李 至

(1.北京自动化控制设备研究所，北京 100074;2.空军装备部驻北京地区第二军事代表室，北京 100037)

0 引言

随着现代战场环境的复杂化，无人机对导航系统的自主性要求更加严苛，卫星拒止条件下单纯依靠惯导系统无法满足无人机的导航精度需求。视觉导航凭借与惯性导航的互补性，与惯导融合成为了一种可靠的自主导航手段，在小型旋翼无人机、地面无人车等领域已得到广泛应用；但对于面向高空场景的大型无人机，仍存在尺度误差难以精确估计的问题，即视觉里程计算出的相对位置、速度信息缺乏绝对量纲，与真值之间具有较大尺度误差，无法为惯导系统提供精确量测信息。

对此，国内外开展了面向无人机领域的惯性/视觉里程计组合导航方法研究。2016年，苏黎世大学的M.Faessler等将轻量级半直接法视觉里程计(Semidirect Visual Odometry，SVO)与多传感器融合框架(Multi-Sensor Fusion，MSF)进行组合，在具有重复和高频纹理的场景中提高了鲁棒性。2016年，Yang Z.等提出了一种不依赖人工标记与有关机械的先验知识的初始化速度、重力方向、视觉尺度和相机-惯性测量单元(Inertial Measurement Unit，IMU)动态外部校准方法。C.Campos 等提出了一种基于最大后验估计的尺度估计方法，先通过纯视觉估计出惯性器件误差，再利用惯性视觉组合估计出尺度误差初值，在低空场景获得了良好表现。2018年，香港科技大学沈劭劼等提出了VINS-Mono，该系统提出了一种在线校准视觉和惯性测量之间时间偏移的方法，通过建立IMU和相机观测数据的目标函数，最小化联合误差的函数，由此获得高精度的实时定位。2021年，翟海庆等利用超声波传感器通过最小二乘法完成尺度估计值的获取，并通过扩展卡尔曼滤波(Extended Kalman Filter，EKF)实现了单目视觉与惯导的信息融合。另外，还有一部分学者采用双目相机方案，通过基线长度为视觉导航系统提供尺度基准，但是由于相机基线较短，该方法并不适用于高空场景。对于机器人、无人车等地面设备，大多采用相机前视安装的方式，通过相机与地面间的高度为系统提供精确尺度基准，该方法同样无法应用于大型无人机。

因此，针对上述情况，本文建立了适应于高空场景的激光测距/视觉里程计误差更新模型，通过因子图优化方法对三种传感器测量值进行组合，并详细分析了尺度误差在无人机平飞运动状态下的可观测性，最后通过机载仿真试验对本文算法在300m高空场景下进行了精度验证。

1 惯性/激光测距/视觉里程计

本文提出的惯性/激光测距/视觉里程计导航方法前端采用特征点法视觉里程计，通过连续图像间匹配的特征点计算无人机相对位置变化。系统框架如图1所示，蓝色矩形框为惯性、相机原始传感器，橙色矩形框为本文引入的激光测距传感器，为系统提供对地高度测量值，三种传感器数据经过BA(Bundle Adjustment)优化融合，对惯性/激光测距/视觉里程计组合导航系统尺度误差进行精确估计(红色矩形框)。

图1 惯性/激光测距/视觉里程计系统框架Fig.1 Framework of inertial/laser ranging/visual odometry system

1.1 坐标系定义及变量表示方法

世界坐标系(系)：坐标系原点取为视觉里程计初始化成功第一帧(0,0,0);轴指向初始化时刻摄像机纵侧方向，向右为正;指向初始化时刻摄像机竖轴方向，向下为正;指向初始化时刻摄像机纵轴方向，向前为正。

相机坐标系(系)：坐标系原点取为相机质心;轴指向摄像机侧轴方向，向右为正;指向摄像机竖轴方向，向下为正;指向摄像机纵轴方向，向前为正。

像素坐标系(系)：原点位于图像左上角;轴指向图像水平方向，向右为正;轴指向图像垂直方向，向下为正，为二维坐标系。

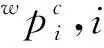
1.2 激光测距量测更新方法

本文提出的惯性/激光测距/视觉组合状态向量为

(1)

其中，为惯导系统状态变量

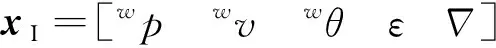
(2)

包括位置、速度、姿态、陀螺漂移以及加速度计零偏。

为视觉里程计系统状态变量

(3)

包括连续帧内世界坐标系下相机的位置、姿态以及特征点位置坐标。在文献[17]中，已对惯导状态更新方法与视觉里程计状态更新方法进行了详细介绍，本节则主要分析激光测距传感器测量值与视觉里程计状态之间的联系，并给出量测更新方法。

如图2所示，相机在运动过程中采集连续地面图像，激光测距机获取当前时刻无人机相对地面高度，由于面向的是高空场景，因此忽略相机光心与激光测距光心之间距离造成的误差，默认二者位于同一直线上。当前地点所在的平面最少可由3个特征点确定，因此选取激光点周围的3个特征点构建平面，并求取其法向量

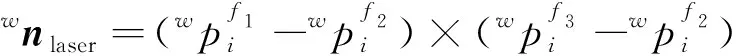
(4)

图2 目标点相对激光测距几何关系示意图Fig.2 Schematic diagram of the geometric relationship between the target point and the laser ranging

(5)

(6)

因此，激光测距测量值的误差方程可以表示为

2δ2+3δ3+

(7)

式中，为与各状态量相关的量测矩阵,为雅可比矩阵形式。

1.3 量测矩阵详细推导

为了方便推导，将式(6)中的复杂项做如下标记

(8)

已知激光测距测量值与惯导状态无关联，所以系统量测矩阵中非零变量只需要对视觉状态量求偏导

(9)

因此，对于矩阵的计算便转化为求解∂∂、∂∂与∂∂的过程。

(10)

3×(15+6+3(--1))||3×3(-)]

(11)

3×(3+3(-))]

(12)

由此，可以得到式(7)中所有的子量测矩阵。

2 系统可观测性分析

组合导航系统各状态变量的可观测性与无人机机动状态密切相关，惯性/视觉里程计组合导航与传统惯性/轮式里程计组合导航方法相比，主要不同点在于高空场景下视觉里程计存在大尺度误差，影响系统可观测性,而其他状态变量在不同机动下的可观测性在多篇文献中已有明确分析结论，因此，本文只针对性讨论尺度误差对其他状态量的影响。

2.1 传统组合模型可观测性分析

无人机飞行时垂直方向上的机动可为惯性器件提供激励，使尺度误差与惯性器件误差解耦，提高可观测性。而在大多数的巡航阶段，无人机需要保持水平姿态巡航，这种平飞机动状态下尺度误差的可观测性降低。本文针对这种情况对所提出的惯性/激光测距/视觉里程计系统可观测性进行分析，即分析尺度误差对本文式(1)中各状态变量的影响。

尺度误差的表现形式为无人机飞行轨迹的缩放，因此只影响到位置、速度以及加速度，对无人机的姿态变化无影响。因此,根据式(1)构建无人机在空中平飞时由尺度误差为主要影响因素的观测向量

(13)

由于尺度误差对姿态无影响，则式(13)中姿态角以及陀螺漂移所对应项为零向量。验证在此机动状态下的系统可观测性，即验证是否属于系统可观测性矩阵的右非零空间，即·=0。传统模型中的惯性/视觉组合模型为文献[17]中式(1)定义，其状态转移矩阵′由文献[17]中式(18)定义，系统量测矩阵′由文献[17]中式(27)定义。则传统组合模型的可观测性矩阵′为

′=′′

(14)

则

′=(--·δ-·+)

(15)

式中，、具体形式由文献[17]中式(47)、式(50)定义，其中

(16)

因此

′=(--·δ-·+)

=(-)

=′·=0

(17)

即证明，属于系统可观测性矩阵右非零空间，亦证明无人机空中平飞机动状态下尺度误差不可观测。

2.2 本文组合模型可观测性分析

本文提出的惯性/激光测距/视觉里程计系统可观测性矩阵表示为

=

(18)

式中，为13节中推导的系统量测矩阵;为系统状态转移矩阵。如1.2节中所述，由空间中3个特征点确定当前地面，所以可将根据变量类型分解为各子观测矩阵，由式(7)中各子量测矩阵可得

=[|||1|2|3]

=[,|,|,|,|,|,1|,2|,3]

(19)

式中，状态转移矩阵的详细表达式在文献[17]中已有明确定义，因此，联立式(6)、式(8)各子观测矩阵的详细表达式如下

,=

(20)

,=

(21)

(22)

(23)

(24)

(25)

同样证明式(13)由尺度误差为主要影响因素的观测向量不属于的右非零空间，即证明·≠0。

·=,·+,·+,·+

,1·1+,2·2+,3·3

([(3-2)×]T2+[(1-

3)×]T2+[(2-1)×]T3)

[(3-2+1-3+2-

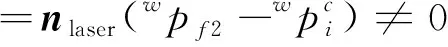
(26)

已知地面特征点与相机位置不在同一平面，因此·≠0，证明了本文提出的惯性/激光测距/视觉里程计导航系统在无人机平飞机动状态下尺度误差可观测，对系统其他状态变量的可观测性无严重影响。

3 机载试验验证

为了验证本文算法的有效性，对算法进行了机载试验验证，试验载机、试验设备及其安装方式如图3所示。

(a) 大疆M600-Pro无人机

(b) 搭载视觉导航样机

(c) 样机安装方式

(d) 飞行试验示意

其中，图3(a)所示大疆M600-Pro无人机为本次试验载机；图3(b)所示为参试视觉导航样机，图中序号1、2、3分别为可见光相机、1km激光测距仪和sbg微惯导；图3(c)与图3(d)给出了机上安装方式与试验飞行过程展示。本次试验地点为北京市六环外室外区域，地面场景为树林及公路等特征较为丰富区域，本次试验飞行高度300m。惯性/激光测距/视觉里程计组合导航系统在空中初始化成功后进行平飞，飞行轨迹为一段正方形轨迹。

经过仿真验证，在高空场景下传统的惯性/视觉里程计算法在缺少纵轴方向上的运动激励时，惯性器件偏差将与视觉里程计尺度误差严重耦合，无法完成初始化。图4给出了目前导航精度、鲁棒性均较为优秀的orb-slam3算法对机载数据的纯视觉仿真结果。

图4 orb-slam3算法纯视觉仿真结果Fig.4 Pure vision simulation results of orb-slam3 algorithm

从图4可以看出，紫色纯视觉里程计导航轨迹具有明显的尺度误差，无法为无人机提供稳定的导航信息，而通过orb-slam3中的惯性/视觉组合导航方法对机载数据进行仿真，结果如图5所示。

图5 orb-slam3惯性/视觉组合初始化位姿漂移Fig.5 Initialization pose drift of orb-slam3 inertial/visual combination

由图5可以看出，在箭头标记处由于高空场景下地面特征平面化，相机无法计算相对地面深度，因此系统无法准确对尺度误差与加表零位解耦，导致系统初始化失败发生位姿漂移。通过对多组不同飞行高度的机载数据进行仿真，orb-slam3算法均初始化失败，验证了此条件下无法完成稳定导航。

而本文提出的惯性/激光测距/视觉里程计算法可以实现尺度误差的精确估计，程序运行界面如图6所示。

图6 300m高度飞行数据程序运行界面Fig.6 Program operation interface of 300m altitude flight data

图7给出了本组试验飞行轨迹及误差对比结果，从图7(b)可以看出，通过激光测距提供尺度基准，尺度误差快速收敛。

图7(a)中紫色轨迹为本文所提算法仿真结果，绿色轨迹为差分卫星基准，可以看出，在初始时刻系统即成功完成了初始化，并稳定完成了后续阶段的导航。本组数据全程飞行距离1.34km，最大位置误差处为14.7m，定位精度为1.09%，本次机载共进行了4次飞行试验，试验结果如表1所示。

(a) 机载试验飞行轨迹对比

(b) 本组数据尺度误差估计结果

(c) 三方向位置误差

(d) 径向位置误差图7 机载试验轨迹及误差对比Fig.7 Track and error comparison of airborne experiment

表1 飞行试验结果统计

4 结论

1)本文建立了惯性/激光测距/视觉里程计组合导航模型，并详细推导了激光测距量测更新矩阵。通过激光测距仪测量的对地高度提供尺度基准。

2)对本文提出的组合导航模型在无人机平飞机动状态下可观测性进行分析，验证了通过引入激光测距实现惯性器件误差与视觉里程计尺度误差解耦的可行性。

3)通过实际机载试验数据，验证了在300m高度无人机平飞状态下，组合导航系统初始化与后续导航精度。经过仿真分析，传统方法无法成功初始化，本文所提算法在机载试验中最远飞行距离2.31km，最大位置误差28.01m，定位精度1.21%，四组试验统计精度优于1.5%，达到地面惯性/视觉里程计定位精度，验证了算法的有效性。