全球股市有效性的动态演化及量化比较研究①

李 燕， 郝晓玲， 李 湛

(1. 上海财经大学信息管理与工程学院， 上海 200433； 2. 怀化学院商学院， 怀化 418000；3. 上海市金融信息技术研究重点实验室， 上海 200433； 4. 东莞理工学院经济与管理学院， 东莞 523000)

0 引 言

有效性市场假说是现代金融理论的一个重要基石，但也是金融学研究领域中一个极具争议性的问题. 关于股票市场有效性的研究，可追溯至 Bachelier[1]提出的股票价格波动近似于随机游走过程.Fama[2, 3]以随机游走模型为基础构建了有效市场的概念，将有效市场定义为：如果证券价格能够迅速且充分地反映所有有关证券价格的信息，便称其为有效率.对股票市场有效性的研究大多建立在随机游走假说的基础之上，认为市场价格时间序列呈现出随机状态[4].但自上世纪70 年代末以来，股票市场涌现出许多有悖于标准金融理论的投资者异常行为及股票市场异象，给传统金融理论带来了极大的挑战.同时，在对有效性市场假说的实证研究中，所获研究结论并不一致甚至获得截然相反的结果，有效性市场假说受到诸多质疑，并引发了巨大的争议[5-8].产生争议的主要原因在于，对市场有效性的研究中，通常存在一个潜意识的先验推理：当前市场有效意味着以后的市场也是有效的，但实际上市场有效性存在时间动态不一致性，呈现出复杂的动态演化行为.

在市场有效性研究中，有两个问题值得探究：一是关于市场有效性程度的度量；二是关于市场有效性的动态演化、集群行为及似周期性研究.

问题1如何度量市场的有效性程度？目前，对股票市场有效性的检验还处于定性层面，缺乏对股票市场有效性程度进行表征的度量指标，进而难以对处于同一有效性阶段的不同股票市场的有效性进行量化比较.

Ramirez等[9]建议从信息熵的方法来研究股票市场的有效性，认为市场有效性是随着时间的推移而变化的，并具有时间尺度效应.Walid等.[10]使用修正的香农熵(MSE)方法对原油市场弱形式效率的时变程度进行分析，所得研究结果表明，WTI市场和欧洲布伦特两个石油市场的弱形式市场效率随时间推移而变化，WTI市场的效率低于欧洲布伦特原油市场的效率.Walid等.[11]采用修正的香农熵对市场有效性进行研究，实证结果表明股票市场有效性随着时间的推移而变化，并且在不同的市场和不同的地理区域具有不同的变化特征. Calcagnile等.[12]通过测量高频时间序列数据的熵来研究金融市场的相对信息效率.Niu等[13]使用多尺度加权排列熵和递归量化分析方法对汇率波动进行研究，实证结果表明，日元/美元有着更高的复杂性，表明日本外汇市场的效率相对更高，而韩国、中国香港和中国大陆等经济体的外汇市场的效率较低.徐梅等[14]引入符号时间序列分析方法，以收益率符号序列修正Shannon熵作为市场有效性的度量，以时变修正Shannon熵刻画市场有效性随时间的变化.

近些年，递归图方法作为分析动态复杂系统的新工具获得快速发展和广泛应用.基于价格(收益率)序列分布的经典“熵”统计模型只能刻画系统的“短程关联”，而递归图方法适合分析时间序列全局状态关联关系，因此基于递归图方法构建的递归熵更能量化度量系统的无序性程度，进而可以度量股票市场弱式有效性程度，解决目前对市场有效性只能进行定性检验的局限性.另外，递归图方法是一种非线性时间序列分析方法，能够解析一维混沌时间序列所暗含的非线性动力学特征.股票市场通常是以非线性的方式对外界信息做出反应，递归图方法能有效解析股票市场对外界信息的反映效率.

问题2股票市场有效性的动态演化及集群行为分析，进一步探究市场有效性是否存在似周期性的演化行为？

对市场有效性动态演化分析的研究文献相继发表在国内外重要学术期刊上.Lo[15]指出市场效率会随着市场和宏观经济条件(衰退、市场崩溃和危机、泡沫)的变化而变化.Kumar[16, 17]通过实证研究发现股票市场的有效性表现出随时间变化的动态行为特征.Ito等[18]实证结果表明，市场效率的程度具有时变演化特征，而且有时国际股票市场表现出共同有效和无效的.Ito等[5]引入市场效率随时间变化程度的概念，建立了一个非贝叶斯时变模型，考察了美国股市是否随着时间的推移而变化，研究发现美国股市的市场效率具有周期性波动行为，周期为30年至40年.Khuntia等.[19]研究了比特币市场中时变收益的可预测性，得出了市场效率随时间而演化的结论.Alves等.[20]通过计算股票市场指数对数收益滑动时间窗内的排列熵来定义股票市场的时变有效性及市场有效性的集群行为，研究结果表明，世界主要股票市场有效性及市场集群行为表现出动态演化特征，股票市场有效性的动态演化可以推动股票市场信息效率的提高，也能降低市场信息效率，使市场的系统性风险变大.周孝华等[21]研究发现我国股票市场效率存在动态变化，无效的时段与金融危机或政策巨变等重大事件联系密切.

近几年，有部分学者开始就金融危机、政治动荡及全球主要的地缘政治事件对股票市场有效性的影响进行研究，MahmoudI等[22]从信息熵的角度，利用450天观察窗和滚动法来研究市场效率的日演变，结果表明Shannon熵系数随时间演化，表明市场的有效率性是动态演化的，在危机时期(金融或政治)，市场效率会下降.Tran等[23]研究也发现在许多重大经济事件期间，股票市场的效率会降低.Kumar等[24]认为在市场崩溃及金融危机期间，经济受到流动性危机、金融恐慌和混乱的市场状况的影响，可能会导致市场预期的非线性动态变化，从而导致在重大宏观经济事件期间，印度汇率市场的效率下降.Lalwani等[25]研究发现新型冠状病毒肺炎危机开始后股票市场的信息效率下降.

针对上述两个问题，本文将从非线性动态演化分析视角来研究股票市场的有效性，探索股票市场有效性的动态演变行为，探究股票市场有效性的演化机理.贡献在于：1)构建了一种股票市场有效性的度量方法.使用递归图方法来提取股票价格(指数)时间序列的动力学特征，如似周期性、可预测性及确定性.在递归图中与主对角线平行的线段长度的分布信息度量了产生时间序列的原动力系统的动力学信息量或随机性的程度.根据这些线段长度的分布信息构建递归熵，它能够度量一维时间序列嵌入到高维相空间中状态矢量的聚集程度，可以度量系统的确定性或可预测性程度.2)使用经验模态分解法、最大熵谱分析法及Fisher 检验研究美国股票市场有效性的似周期性演化行为.3)金融危机期间全球股票市场有效性的集群行为研究.研究发现在经济危机期初股票市场有效性呈现出急剧下降，在金融危机中后期逐渐趋于稳定.因此单纯地把市场认定为有效或无效都是错误的，市场有效性在相对无效和相对有效间反复波动，当市场环境急剧变化，市场有效性也会产生变化.本文提出采用组合方法(EMD+熵谱图)来研究股票市场的周期性演化行为，将以前不同文献的关于市场有效性的研究成果纳入统一分析框架里，并进行了实证检验，结果表明该框架对探究市场有效性具有现实可操作性.

1 市场有效性定义及量化表征

在以往的研究中，不同学者对市场有效性的定义有所差异，本文首先对股票市场有效性的定义进行了归纳和梳理，见表1所示.借鉴以往的研究成果，市场有效性体现的是市场对外界信息反映效率，此外，股票市场通常是以非线性的方式对外界信息做出反应，递归图方法能更有效地解析股票市场对外界信息的非线性反映效率，基于递归图方法构建的递归熵更能量化度量系统的无序性程度，进而可以度量股票市场弱式有效性程度，因此，采用递归熵来表征市场的有效性.

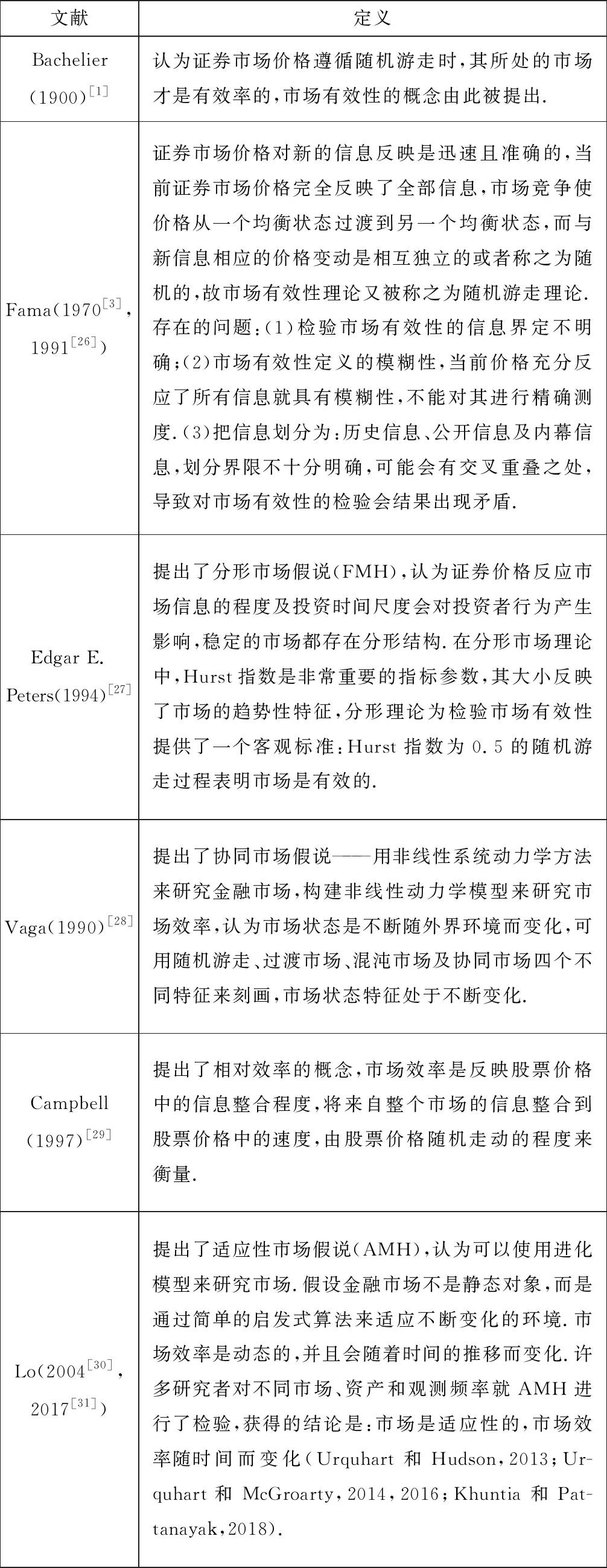
表1 市场有效性的定义

续表1

2 递归图方法及递归熵

近几年，越来越多的研究人员使用递归图方法来研究股票市场、外汇市场、期货市场、黄金及国际原油等市场价格时间序列的混沌特征，分析这些金融市场所暗含的非线性结构、规律及预测问题[32～34].

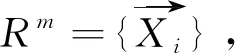
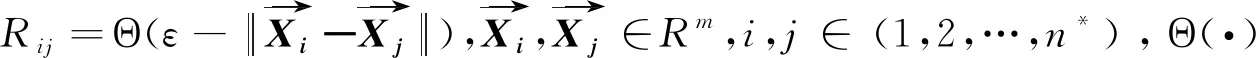
下面使用递归图及递归熵来分析正弦信号sin(6*π*t)，采样频率为1 000 Hz，采集2 000个数据；洛伦兹信号取δ=10,b=8/3,r=28，采样频率为50 Hz 的情况下x(t)分量所产生的时间序列.

从图1可以看出，正弦时间序列呈现出周期性的波动，数据序列非常有序；洛伦兹信号序列呈现出类周期性波动，数据序列比较无序，是混沌时间序列；随机数序列是随机波动的，数据序列完全无序.在图2中，从三个时间序列数据的递归图可以看出正弦序列的递归图非常规则，有完整的与主对角线平行的直线，说明系统具有完全的确定性，与主对角线平行的直线之间有均匀的空白带，说明数据具有规则的周期性.从洛伦兹序列的递归图可以看出，递归图具有一定的规则性，有一些不完整的与主对角线平行的线段，说明系统具有一定的确定性，与主对角线平行的直线之间有不均匀的空白带，说明数据序列具有不完全的周期性.从随机数时间序列的递归图可以看出，递归图毫无规则，没有与主对角线平行的线段，说明系统没有确定性或可预测性.由此可以看出，递归图可以明显区分周期性数据、混沌时间序列数据及随机时间序列数据的动力学特征.正弦时间序列数据的递归熵为3.334 9，洛伦兹时间序列数据的递归熵为2.03，随机时间序列数据的递归熵为0.383 5.由递归熵的计算结果可以看出正弦序列的递归熵大于洛伦兹序列的递归熵，洛伦兹序列的递归熵大于随机数序列的递归熵.这符合正弦序列的规则性大于洛伦兹序列的规则性，洛伦兹序列的规则性大于随机数序列的规则性.因此递归图方法及递归熵可以用来分析股票价格时间序列数据的无序性程度及市场有效性程度.

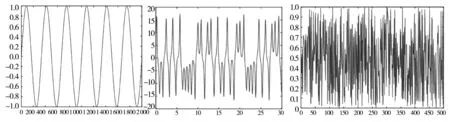
(A)正弦信号序列 (B)洛伦兹信号序列 (C)随机数序列

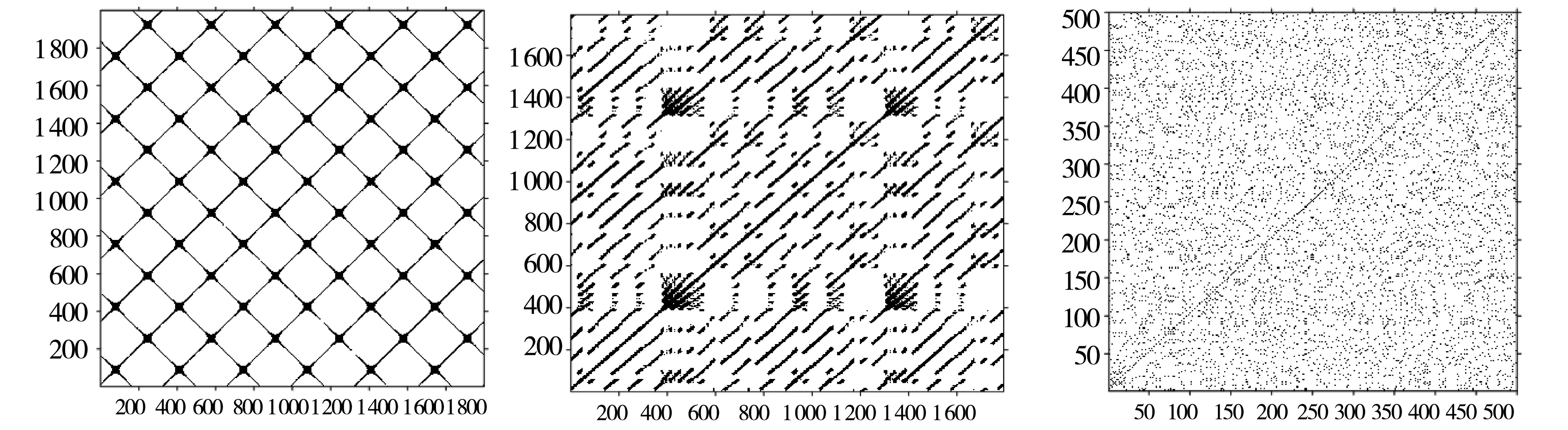
(A)正弦序列递归图 (B)洛伦兹序列递归图 (C)随机数序列递归图

3 全球股票市场的有效性量化比较研究

在自然科学研究中，要对一个系统的演化行为进行研究，首先需要根据先验知识确定该系统可能受到哪些因素的影响，因素之间的相互作用关系.再依据研究对象、研究目的及研究可行性的需要，且遵循一定的原则从全部影响因素中选出最本质、最重要的因素作为研究系统的状态变量，再根据相应理论构建出控制这些状态变量演化的动力学微分方程体系.假设一个系统可以由m个状态变量所决定，各状态变量是时间t的函数，即yi=yi(t)，则可以构建如下微分方程组来描述系统的演化行为.

随着时间的演化，可以得到一系列的系统状态向量Yi=(y1,y2,…ym),i=1,2,…,m，这些状态向量点就会在m维相空间中形成系统的状态运行轨迹，状态轨迹的变化表示了系统演化的动力学行为.但股票市场不同于自然科学中的研究对象，很难完整地界定出影响股票市场系统的状态向量集，因此就不能够构建出股票市场系统演化的微分方程体系.对股票市场系统的研究，通常仅仅只能够获得股票价格的一维时间标量序列，而这个标量序列是m维相空间中的点向一维空间的投影所得.一方面，这样的一维时间序列数据直接能够提供的关于股票市场动力学特征信息十分有限；另一方面，关于股票市场动力学特征的所有信息却都隐含在该一维时间序列中.因此对股市系统的研究，可以使用物理学中重构相空间的方法把一维时间价格序列嵌入到高维相空间中，这样股票市场演化的动力学行为特征，可以在一个拓扑性质不变的高维相空间中，通过状态向量在相空间中的运行轨迹变化得到体现，进而就可以研究股票市场演化的动力学行为特征.相空间重构的方法对那些无法构建出系统动力学方程的复杂系统的研究是一种非常有效的研究方法.递归图方法是在相空间重构的基础上，能够在二维递归图上通过直观分析高维相空间中状态向量的递归性行为，进而研究复杂系统动力学行为的方法.对股票市场有效性的研究采用这种数据驱动的研究方法，此方法不需要对股票价格时间序列数据做任何前提假设，而目前对股票市场有效性检验的方法都需要对股价时间序列数据设定一定的前提假设，而这些假设通常并不符合实际情况.

下面使用递归图方法及递归熵对14个被列为发达国家(地区)的金融市场(澳大利亚、奥地利、比利时、瑞士、新西兰、法国、德国、中国香港、日本、荷兰、新加坡、西班牙、英国和美国)和12个新兴国家(地区)的金融市场(阿根廷、巴西、中国、埃及、印度、印度尼西亚、以色列、韩国、马来西亚、墨西哥、俄罗斯、中国台湾)的股票市场的有效性进行量化比较研究.由于各国股票市场指数的基数不一样，所以在接下来的分析中，使用各国股票市场主要指数的日收益率进行分析.首先使用递归图方法来分析一下美国道琼斯工业平均指数每日收益率序列(2012年01月03日至2018年09月26日)，使用C-C算法可得时间延迟为7，使用虚假邻近点法可以确定嵌入维数为6(图3(A))，进而得到美国道琼斯工业平均指数每日收益率序列的递归图，如图4(A)所示.对上证综合指数每日收益率序列(2012年01月04日至2018年09月21日)，使用C-C算法可得时间延迟为3，使用虚假邻近点法可以确定嵌入维数为7(图3(B))，进而得到上证综合指数每日收益率序列的递归图，如图4(B)所示.

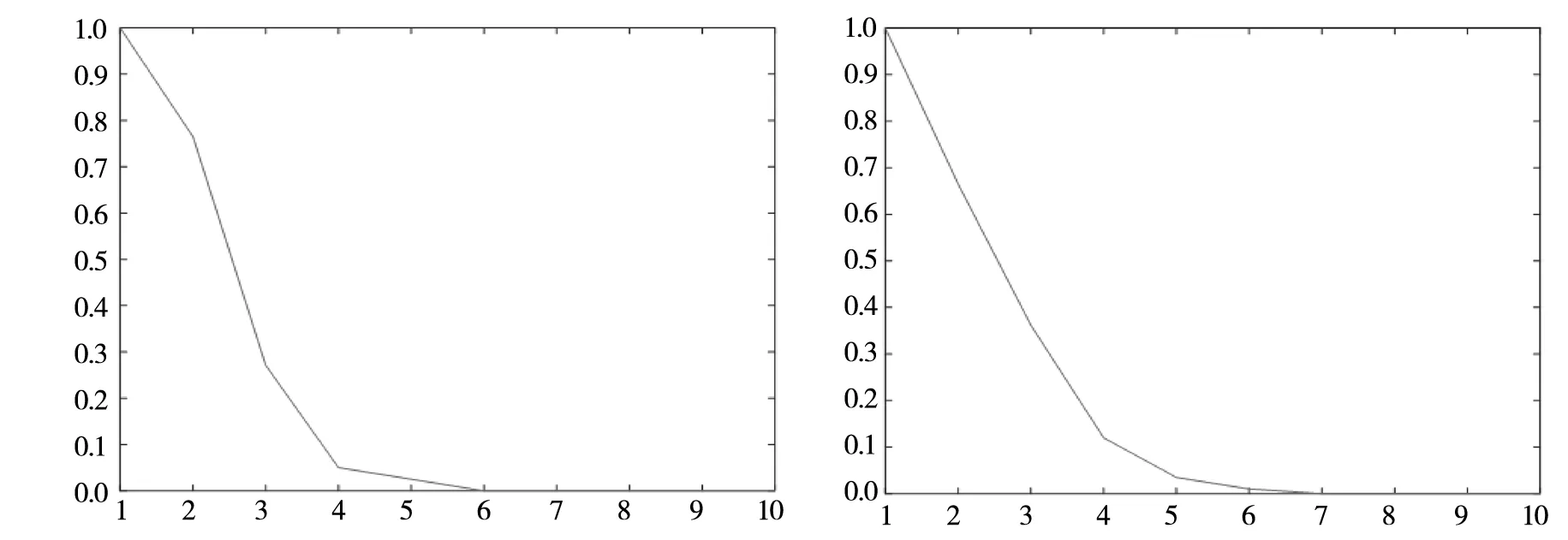
(A)道琼斯工业指数最邻近误差率随嵌入维数变化 (B)上证综合指数最邻近误差率随嵌入维数变化

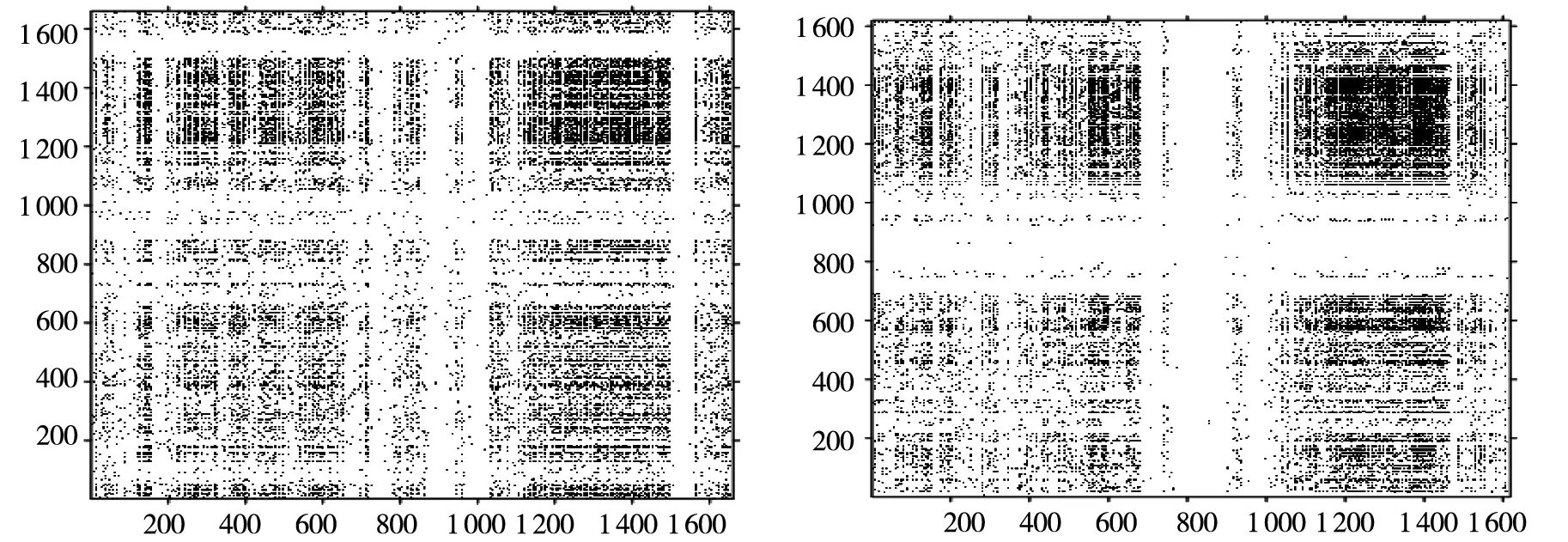
(A)道琼斯工业指数日收益率递归图 (B)上证综合指数日收益率递归图

从美国道琼斯工业平均指数日收益率及上证综合指数日收益率的递归图可以看出：两者的递归图都呈现出一定的规则性，同随机数序列所产生的递归图具有明显的差异，而且两者的递归图具有类分形自相似性结构，因此两个市场指数的日收益率序列不是随机游走序列，两个市场均不是强式有效.美国道琼斯工业平均指数日收益率序列的递归熵为0.426 2，上证综合指数的日收益率序列的递归熵为0.475 3，表明美国道琼斯工业平均指数日收益率序列的有序性要弱于上证综合指数日收益率序列，表明在此时间段美国股票市场的有效性要强于中国股票市场，这与大多数研究文献获得的研究结果一致，说明递归熵可以有效衡量股票市场的有效性程度.接下来进一步研究全球其它股票市场指数日收益率序列的递归熵及对各市场的有效性进行量化比较研究.

使用递归图及递归熵分析荷兰AEX指数(AEX)，澳洲普通股AS30指数(AS30)、奥地利ATX指数(ATX)、比利时BEL20指数(BEL20)、巴西BOVESPA指数(BOVESPA)、道琼斯工业平均指数(DJI)、法国CAC40指数(FCHI)、英国富时100指数(FTSE)、德国DAX指数(GDAXI)、埃及HERMES指数(HERMES)、中国香港恒生指数(HIS)、巴西BOVESPA指数(IBOV)、纳斯达克指数(IXIC)、印尼雅加达综合指数(JKSE)、富时马来西亚交易所KLCI指数(KLCI)、马来西亚吉隆坡综合指数(KLSE)、韩国KOSPI指数(KS11)、马德里General指数(MADX)、俄罗斯Micex指数(MCIX)、阿根廷Merval指数(MERVAL)、墨西哥IPC指数(MEXBOL)、日经225指数(N225)、印度CNX Nifty指数(NIFTY)、纽约证交所综合指数(NYA)、新西兰50指数(NZSE50FG)、印度孟买30指数(SENSEX)、瑞士市场指数(SMI)、富时新加坡海峡时报指数(STI)、以色列TA-100指数(TA100)、中国台湾加权指数(TWII).收集了从1918年01月03日至2018年09月26日之间的全球主要股票市场指数数据，约20万个交易数据.由于每一个股票市场成立时间有先后，并且有些股票市场之间在成立时间上差距上百年时间，所以进行同时间段对比不合适，因为市场发展阶段不一样.把1 000个交易日划分为一个阶段，这种对比更为合适，且这样划分可以分析股票市场的有效性在不同发展阶段的演化情况.

对全球主要股票市场指数日收益率序列的递归熵值及对同一股票市场指数日收益率序列的递归熵值在各时间阶段进行对比分析，可以得到如下结论：1)一般情况下，股票市场在成立之初的三年时间里有效性程度较低，但在随后六年时间里，随着市场法律规章制度的不断完善，各国股票市场的有效性程度将稳定在彼此互异的某一区间内波动.新兴市场国家由于在股市组建之初就能借鉴成熟资本市场的市场管理经验，所以在成立之初时市场的有效性程度一般要高于发达国家股票市场在成立之初时的有效性程度.比如在发达国家(地区)市场中，成立之初三年时间里比利时、奥地利、中国香港、德国、荷兰、英国、新加坡、新西兰股票市场指数的递归熵均大于2，而新兴市场国家(地区)如墨西哥、韩国、以色列、中国台湾、印度、埃及和中国深市股票市场指数的递归熵均小于1. 2)一个国家(地区)发生社会动荡会影响到该国(地区)股票市场的有效性.比如，法国社会在2017年～2018年出现动荡，该国股票市场的有效性程度急剧下降，发生社会动荡之前法国股票市场的有效性程度较高，但最近三年该国股票市场指数收益率序列的递归熵达到2.755 3，市场有效性急剧下降；墨西哥最近十年由于社会安全局势不断恶化催生政治变局，该国股票市场指数收益率序列的递归熵由未发生社会动荡的0.517 0逐渐增加到2.580 0，股票市场有效性急剧下降.同时期，社会局势较为稳定的国家，股票市场有效性表现较为平稳，未出现较大波动.3)股票市场经过大约10年时间的完善发展之后，每个国家的股票市场的有效性通常会稳定在彼此互异的某一水平上波动.Aluko[39]研究了2000年～2014年期间撒哈拉以南非洲11个国家股市的有效性，认为法律制度的有效性并不能促进撒哈拉以南非洲国家股市的发展，这和本研究所得结果一致. 4)通常认为股票市场的有效性只会由弱到强的单向发展，但从时间动态演化的视角对各国股票市场在各阶段的有效性进行量化分析可以得出股票市场的有效性呈现出较为复杂的动态演化特征，在相对有效和相对无效中反复波动.如从美国道琼斯工业指数可以看出美国股票市场的有效性呈现出一种类周期性动态演化，在下文中对这个问题会进一步展开研究. 5)2008年爆发了全球金融危机，各国股票市场的有效性均出现异常波动，全球股票市场的有效性普遍下降，这说明金融危机对市场有效性具负向效应，在下文中会做进一步详细分析.

下面进一步分析在2007年～2008年全球金融危机期间各国股票市场有效性的变化情况，截取2005年01月03日～2008年12月31日市场指数日收益率数据，采用移动窗口分析方法，窗口长度设为250天，窗口移动时间为2天.2008年金融危机大约在2007年06月开始发生，把2005年01月03日～2007年06月31日作为危机前，把2007年07月01日～2008年12月31日作为危机发生阶段，比较危机发生前和危机发生阶段各国股票市场有效性的变化.从图5可以看出，金融危机期间各国金融市场主要市场指数的日收益率序列的递归熵都有一个明显的上升过程，说明在金融危机期间各国金融市场的有效性都存在一个下降的阶段，如在2008年，美国三大市场指数的日收益率的递归熵都有一个非常明显的急剧上升，市场有效性急剧下降.这个研究结果与实际股票市场交易状态相一致，随着股票市场崩盘事件的持续发生，市场交易者逐渐处于非理性交易状态，导致市场有效性急剧下降.进一步从表2可以看出： 1)除奥地利、比利时、新西兰、印度及墨西哥股市，在金融危机期间市场指数的递归熵的均值相比危机前均出现上升.从图5可以看出，2008年奥地利及墨西哥股票市场的递归熵在危机期间出现过急剧拉升的阶段，市场有效性出现过急剧下降的过程，比利时股票市场在2007年也出现过递归熵急剧拉升的阶段.这三个股票市场的递归熵均值在危机期间没有出现上升，出现这种不同于其它国家的现象，原因在于每个国家金融危机发生时点不同及时间窗口截取.新西兰股票市场在金融危机期间的有效性的变化异于其它国家股票市场的特征.原因在于选取的是新西兰50指数，该指数是新西兰股票市场中市值最大的 50 只股票所组成，在金融危机期间，新西兰股票市场在2008年就实现了最终反弹，而此时其它股票市场都处于持续崩盘中，市场交易的非理性程度较高，市场有效性持续下降，但新西兰股票市场已经企稳，市场有效性已经处于逐渐恢复阶段. 2)危机发生阶段市场指数的递归熵的最低值及最高值相比危机前基本都出现上升现象，尤其是递归熵的最高值都出现大幅上升，说明危机期间各市场均出现过有效性大幅下降的过程. 3)在未发生金融危机期间，美国股票市场的有效性比其它大多数国家高，但在金融危机期间美国股市三大市场指数的递归熵都出现了一个明显的急剧上升过程.总的来说，2008年全球金融危机期间，各国股票市场的有效性均出现异常波动，全球股票市场的有效性普遍下降，金融危机对市场的有效性具负向效应.

表2 全球主要股票市场指数收益率序列递归熵

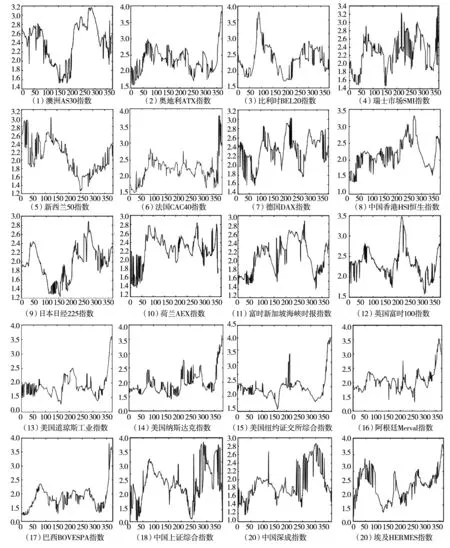
图5 2007年～2008年金融危机期间股票市场有效性变化

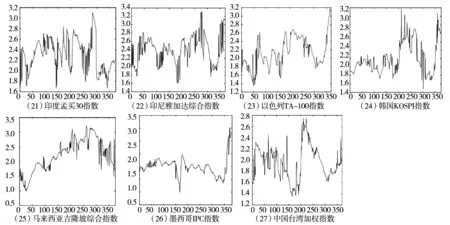
续图5

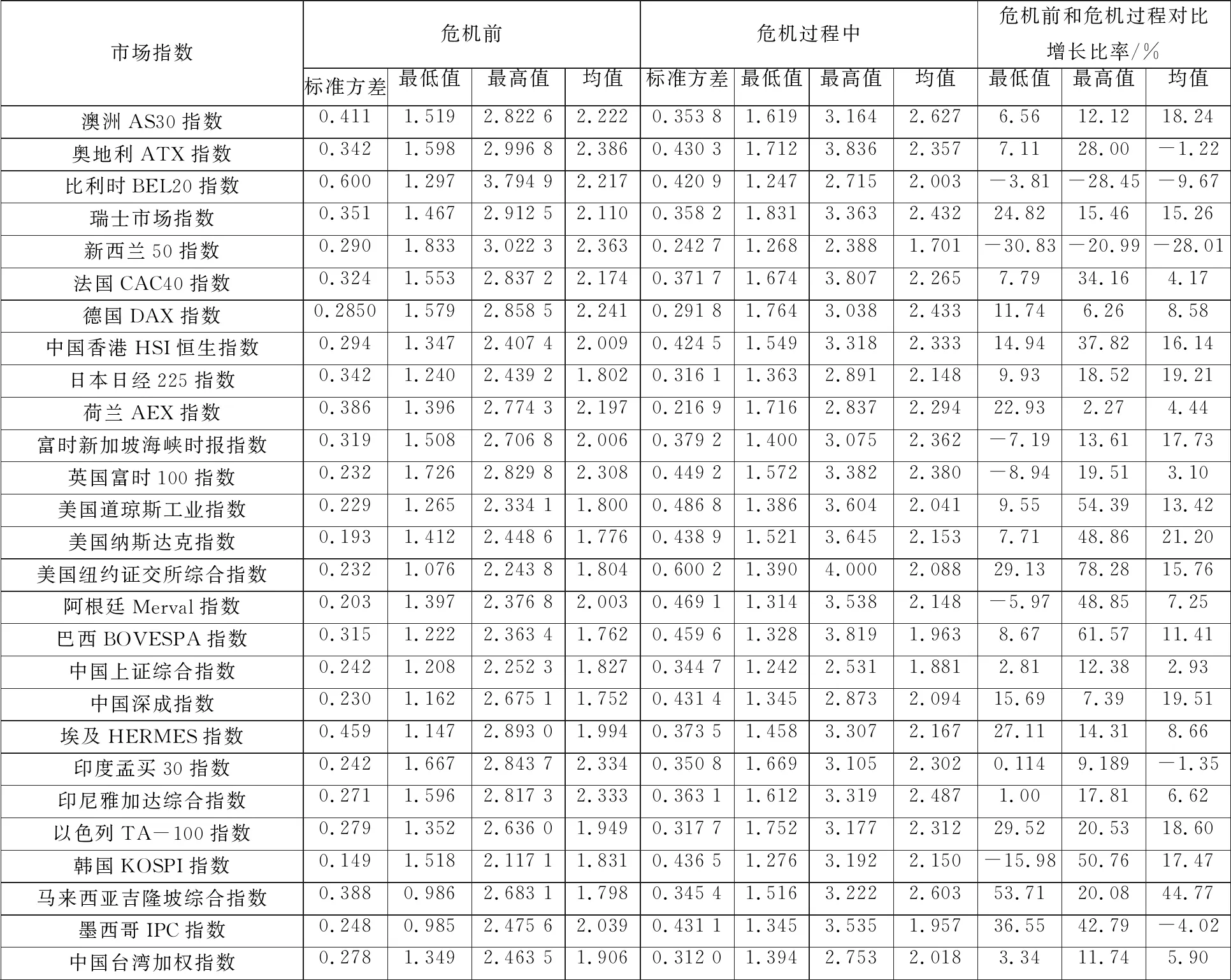
表3 2007年～2008年全球金融危机期间各国股票市场递归熵

下面进一步分析最近100年间，影响全球的金融经济危机事件中股票市场有效性的变化.由于道琼斯工业平均指数历史悠久，其它股票市场在部分金融危机事件发生时并未成立，没有数据可供研究.所以此部分选取美国道琼斯工业平均指数作为研究对象，分析金融危机发生时美国股票市场有效性的变化.对1929年～1933年经济大萧条、1973年～1975年由石油危机引发的经济危机、1987年～1988年“黑色星期一”金融危机及1999年～2001年间的互联网投机泡沫这四次全球重大金融经济危机事件进行分析.收集1927年01月03日～1933年12月29日、1971年01月04日～1975年12月31日、1985年01月02日～1988年12月30日、1995年01月04日～2001年12月31日四个时间段的道琼斯工业平均指数日收益率数据，采用移动窗口分析方法，窗口长度设为250天，窗口移动时间为2天.由图6可以看出，在经济危机期初股票市场有效性呈现出急剧下降，在金融危机中后期逐渐趋于稳定.因此单纯地把市场认定为有效或无效都是错误的，市场有效性在相对无效和相对有效间反复波动，当市场环境急剧变化，市场有效性也会产生变化.

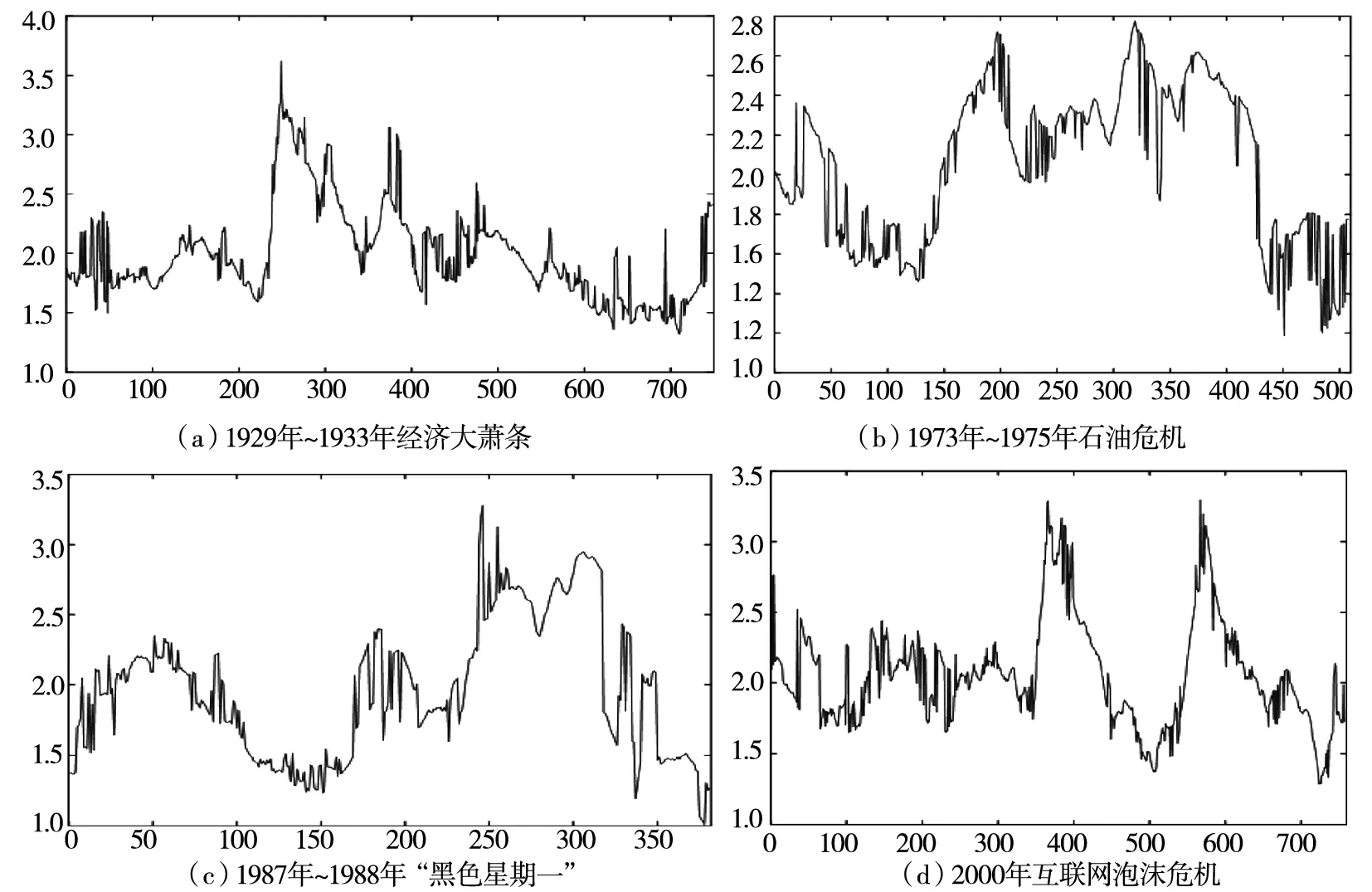
图6 经济危机期间美国股票市场递归熵值变化

下面进一步研究在7日、15日、30日、60日及90日不同时间尺度下全球主要股票市场的有效性， 计算结果，如表4所示.

从表4可以得出：1)股票市场的有效性呈现出时间尺度效应，不同时间尺度下市场有效性不同；2)一般情况下随着时间尺度的增大，市场有效性增强，如新西兰股票市场、韩国股票市场及美国股票市场等，但部分股票市场的有效性随着时间尺度的增大而变弱，如澳大利亚股票市场、中国台湾股票市场. 3)使用层次聚类方法来综合分析各时间尺度下股票市场有效性的分类，如图7所示.比利时、瑞士、荷兰、中国沪市、奥地利及阿根廷股票市场的有效性较为接近；日本、新加坡、德国、韩国及马来西亚股票市场的有效性较为接近；中国香港、印度尼西亚、西班牙、印度股市有效性较为接近；美国、巴西及以色列股市有效性较为接近，新西兰、埃及和法国股票市场有效性较为接近，在上文分析2007年～2008年金融危机期间市场有效性变化时，从图5可以看出，这三个国家股票市场的有效性出现极为相似的急剧下降；墨西哥、澳洲、英国及中国深市股票市场的有效呈现出不同于其它国家(地区)股票市场的有效性，表现出不同时间尺度下股票市场的有效性差异较大.

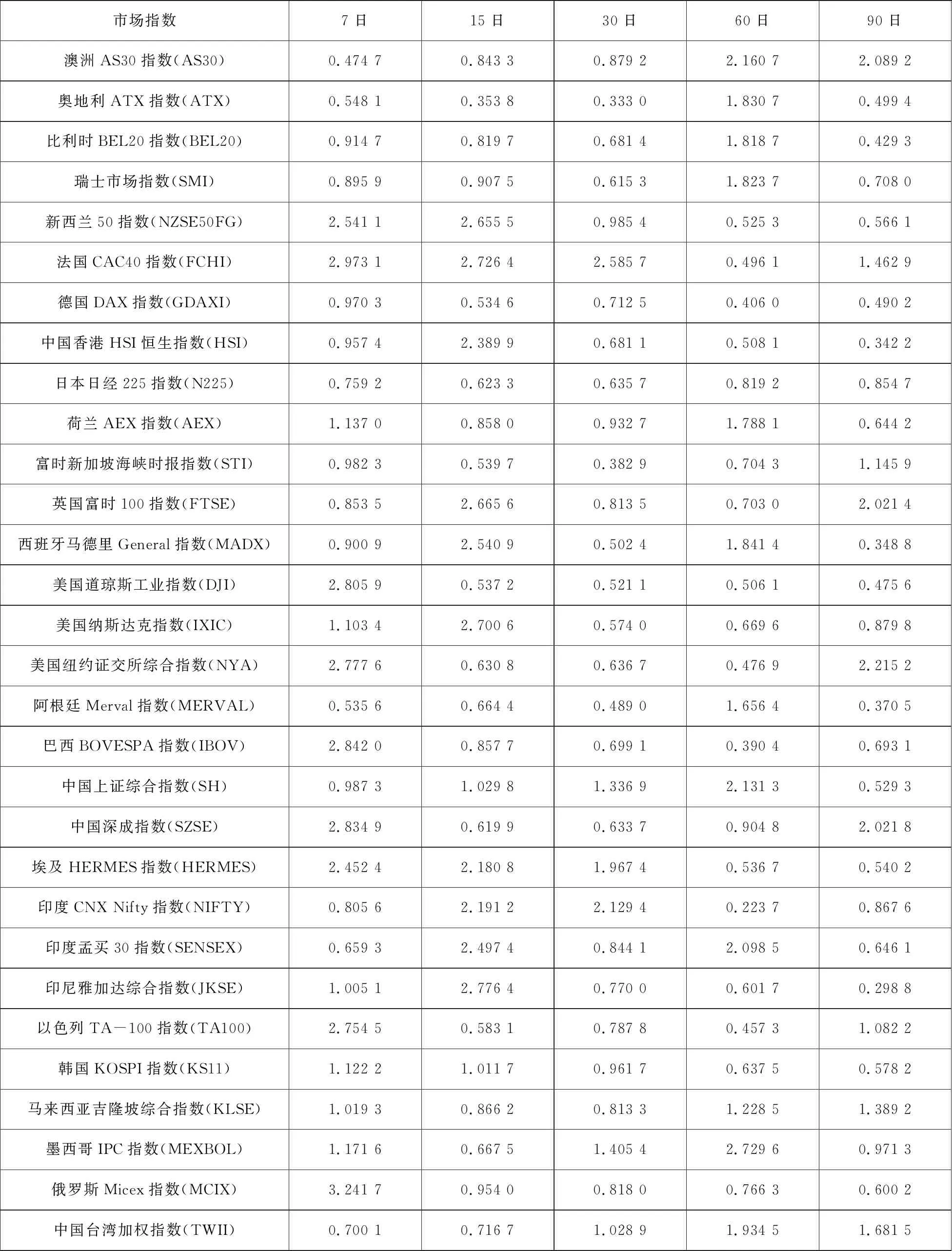
表4 7日、15日、30日、60日及90日不同时间尺度下股票市场指数收益率序列递归熵

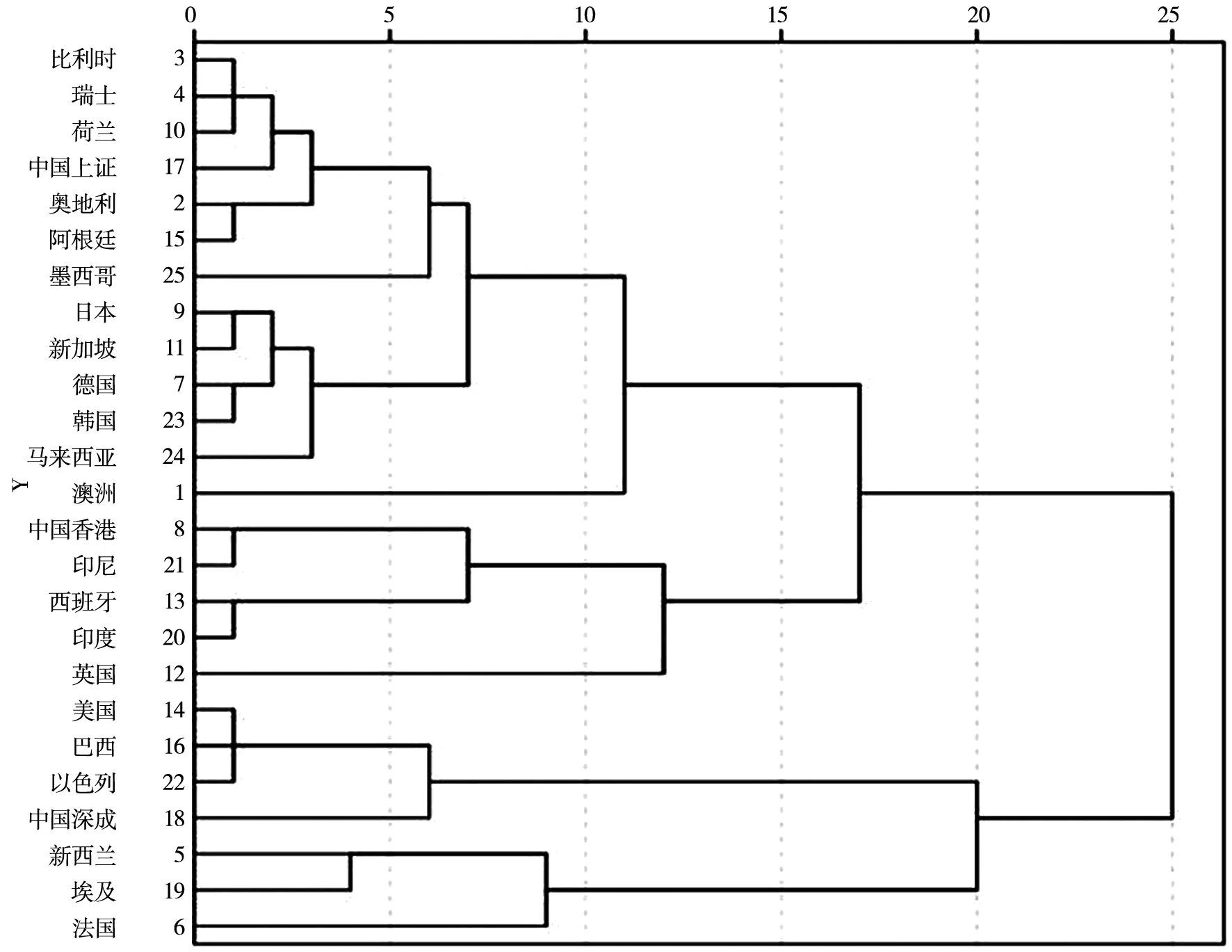
图7 各国股票市场的有效性分层聚类分析

4 股票市场有效性的动态周期性演化分析

以1 000个交易日为时间段的全球股票市场有效性分析中，美国道琼斯工业平均指数日收益率序列的递归熵呈现出类周期性演化行为.美国道琼斯工业平均指数已经有100多年的历史(收集了1918年01月03日～2018年09月26日间该指数的日收益率数据)，相比其它股票市场指数有更为丰富的历史交易数据来对市场有效性及市场有效性的动态演化问题进行研究.在接下来的研究中，把时间尺度细化，以250个交易日(一年大约有250天进行股票交易)为时间段对美国道琼斯工业平均指数日收益率进行研究，该指数日收益率序列在各时间阶段的递归熵，如表5所示.

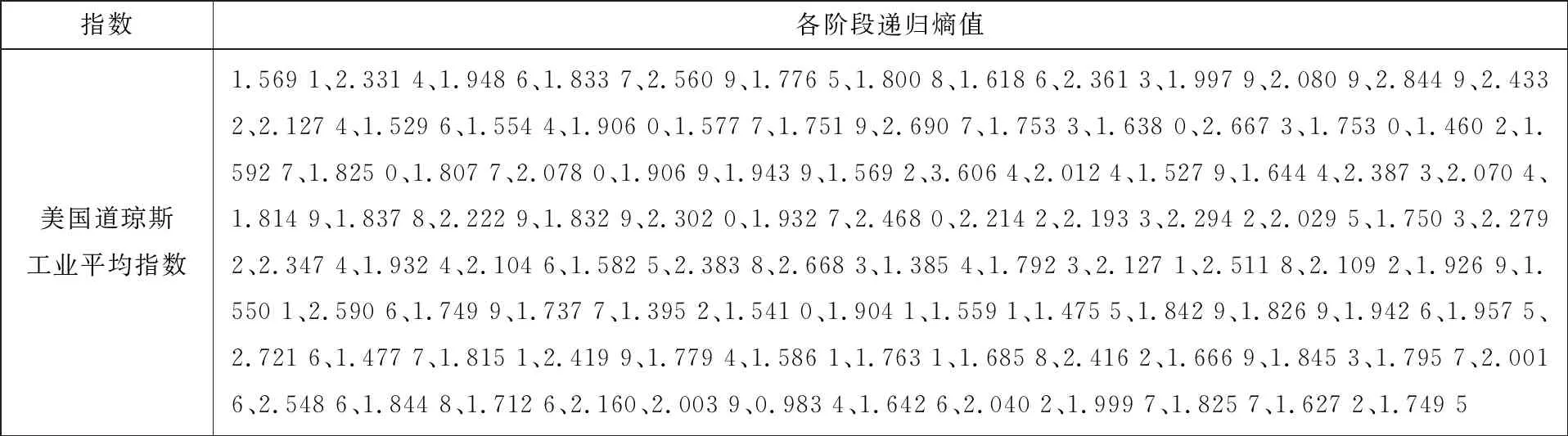
表5 美国道琼斯工业平均指数各阶段递归熵

由表5及图8可知，美国股票市场的有效性呈现出波动性，并不是通常所认为的股票市场有效性仅是从弱到强单方向发展.美国股票市场的有效性呈现出由“相对有效”——“相对无效”的反复波动.由图8(B)可以看出美国股票市场的有效性呈现出状态重现现象，并且出现间距不同的与对角线平行的直线结构，说明递归熵序列存在不同长度的周期性行为.

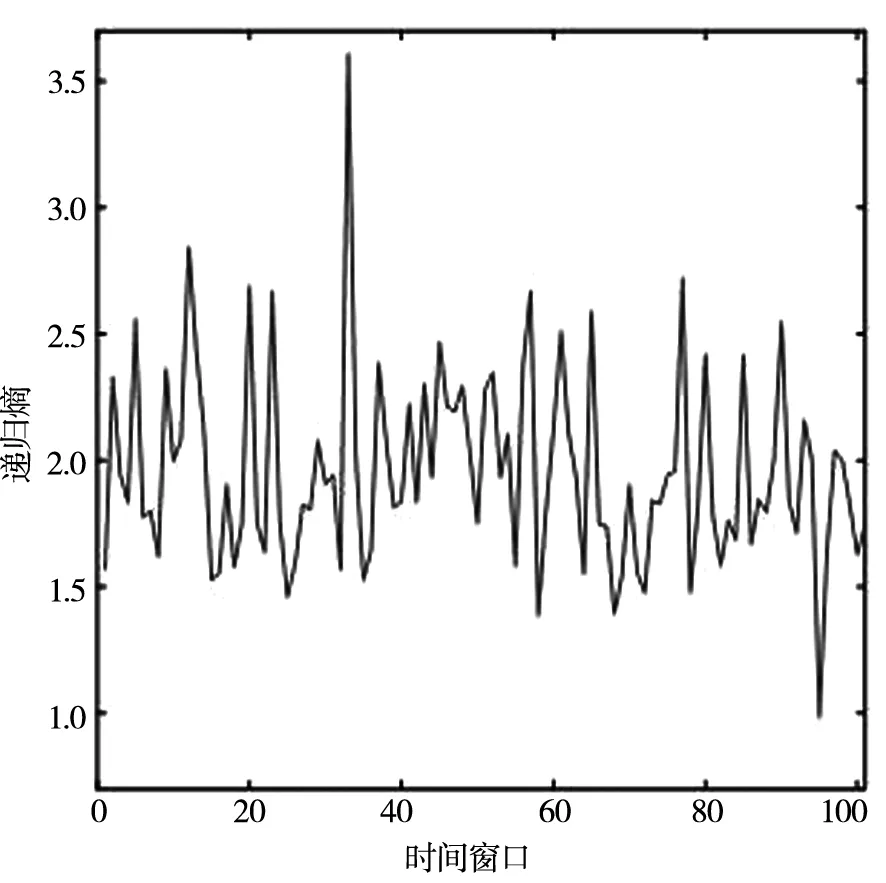
(A)道琼斯工业平均指数递归熵序列 (B)道琼斯工业平均指数递归熵序列的递归图

下面使用Huang[40]构建的经验模态分解方法(empirical mode decomposition，EMD)来分析美国股票市场有效性的周期性行为.经验模态分解方法是一种自适应信号时频处理方法，非常适用于对非线性非平稳信号进行分析处理.EMD方法的基本思路是：为了分析信号的瞬时频率，希望把信号分成被称为内禀模态分量(intrinsic mode functions, IMF)的非周期循环分量.EMD方法的优点不仅在于可以直观的提取序列的趋势，而且可以突出信号的局部波动，提供不同周期模态的模态，作为一种突出局部频率变化的滤波器，EMD可以分析经济时间序列局部的变化规律[41].对道琼斯工业平均指数收益率序列的递归熵序列进行 EMD 滤波操作，到第五阶时 IMF停止分解，最后的残余项表示递归熵序列的宏观趋势，如图9所示.五个不是严格周期循环序列所隐藏的平均周期随着频率的减小而增大，说明了美国股票市场的有效性在不同频率上存在周期性行为，下面进一步对每个IMF分量，采用最大熵谱估计方法对它们进行周期分析.

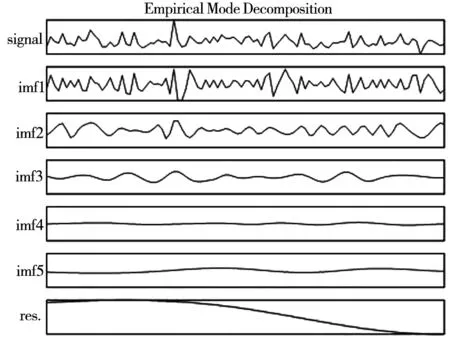
图9 各阶IMF分量序列

对于时间序列周期性的提取，Burg(1967)构建了最大熵谱估计方法，该方法是以自回归模型(AR)为基础的一种参数谱估计方法.最大熵谱估计法具有很高的分辨率，且非常适合于短时序列分析的现代谱分析方法.此方法有效解决了经典谱估计方法需要主观假定实测以外数据的缺陷，从而使序列周期性提取的主观性程度降低，主观偏见变小.实践中，最大熵谱估计方法获得的主要周期比较精确，该方法已经被广泛应用于化学、信号处理、经济学等研究领域.在进行最大熵谱估计方法时，确定自回归最佳阶数比较关键，本文采用FPE准则来确定自回归的最佳阶数r，最大试验阶数为30，选取FPR(r)的最小值所对应的阶数为自回归最佳阶数，各阶IMF分量的FPR(r)值，如图10所示.

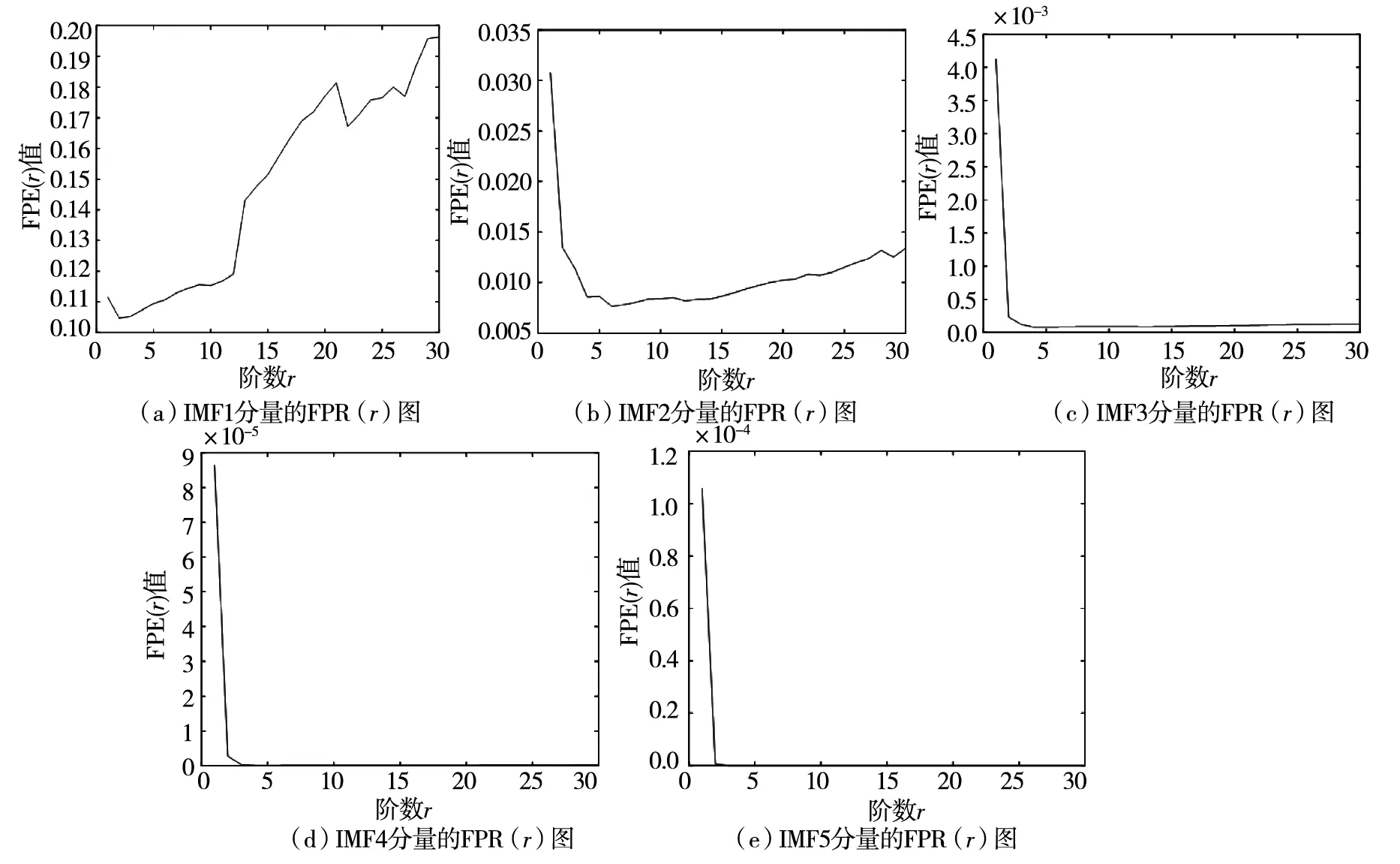
图10 IMF分量的FPR值的变化图

从图11(A)可以看出，在高频率上，美国股票市场的有效性存在长度约为1.7年的周期.从图11(B)可以看出在第二高频率上，美国股票市场的有效性存在两个不同长度的周期(约为4年及3年).在第三频率上，美国股票市场的有效性存在约为6年的周期.在最后两个低频率上，美国股票市场的有效性分别存在约为11年及25年的周期.在第三、第四及第五个频率上，熵谱图都具有十分锐利的单峰，说明周期性比较显著，下面会进一步使用Fisher 检验方法对这些周期性的显著性进行检验.在第三频率上，美国股票市场的有效性存在约为6年的周期，第二频率上，美国股票市场的有效性存在约为3年到4年的周期.英国经济学家 Kitchin[42]通过研究1890年～1922年间英国及美国的物价、生产、就业、银行结算、利率等指标，得出经济周期实际上有主要周期与次要周期两种，次要周期一般为3年～4年一次的短周期.美国股票市场的有效性在第二和第三频率上的3年～6年的波动周期与基钦短周期经济理论中的3年～4年经济周期相吻合.在第四频率上，美国股票市场的有效性存在约为11年的周期，这与1860年法国经济学家朱格拉提出的经济周期为10年左右的经济周期理论相吻合.在第五频率上，美国股票市场的有效性存在约为25年的周期，这与1930年美国经济学家库涅茨提出的一种为期15年～25年的经济周期接近.这就产生了一个值得深入研究的问题，股票市场的有效性或许与经济周期之间存在某种关系，对这个问题的研究有助于获得对股票市场有效性更加深刻的认识.

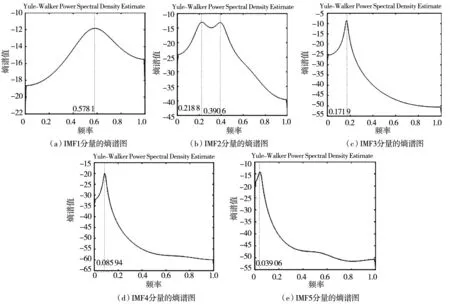
图11 各阶IMF分量的熵谱图

使用经验模态分解及最大熵谱估计方法提取出美国股票市场有效性的周期后，需要对这些周期的显著性进行检验.这是因为股票指数收益率序列的白噪声可能会导致出现虚假的熵谱峰值.对这些周期的显著性检验，使用周期图方法中经常使用的Fisher 检验来检验出现的熵谱峰值是否比白噪声序列的情形要显著.查阅周期性显著性检验的Fisher检验表[43]，获得0.05显著性水平下的临界值，如表6所示.从表6可以看出，五个频率上的周期性在5%的显著性水平下，P值均大于0.05显著性水平下的临界值，全部通过显著性检验，说明美国股票市场的有效性的周期性是显著的.

表6 周期的Fisher 检

5 研究结果与已有文献研究结果的对比分

国内外学者对股票市场有效性问题进行了大量研究，获得了丰富的研究成果，研究方法也具有多样化，下面就论文研究结果与已有对沪深股市有效性的研究文献的结果进行对比分析.

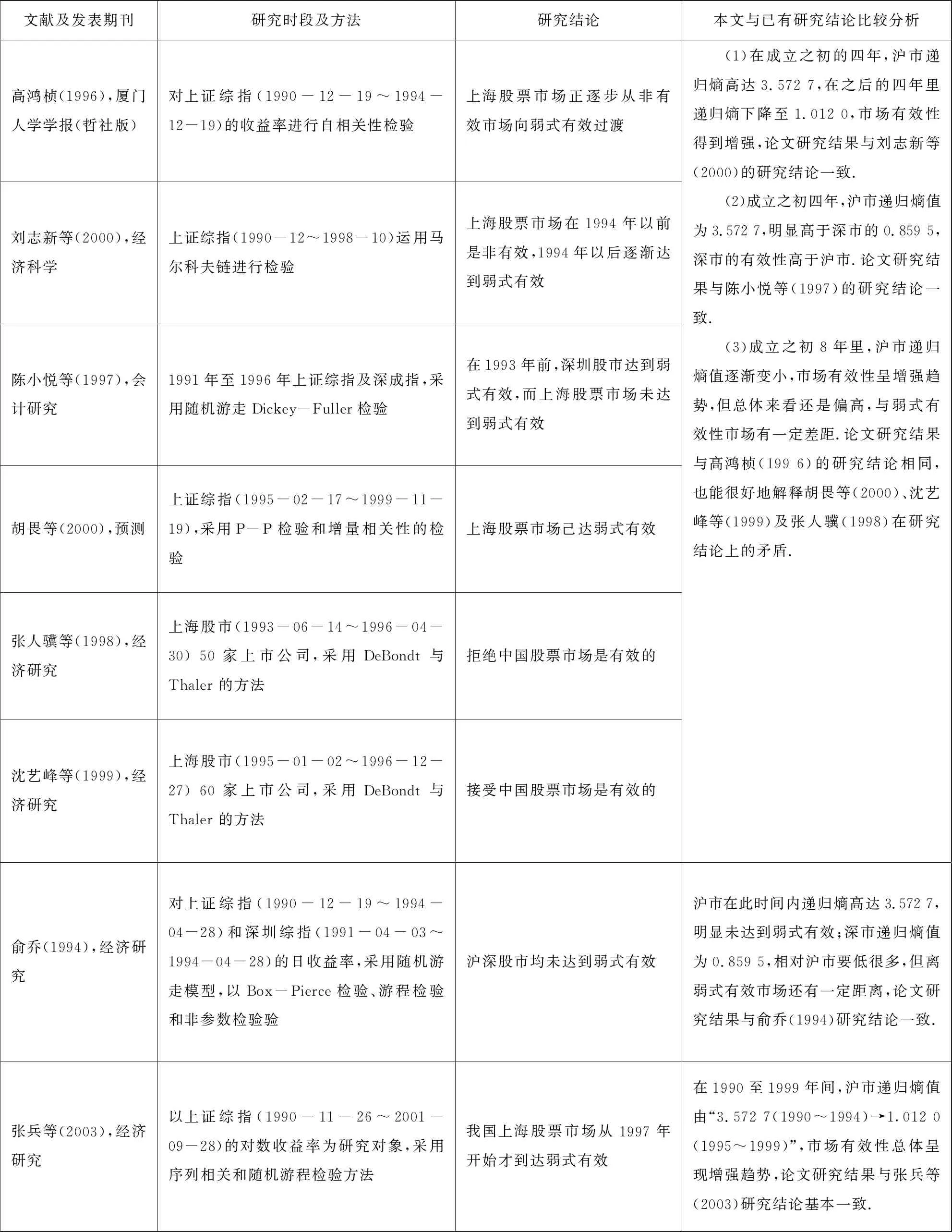
表7 本文研究成果与已有研究成果的共性与差异之处

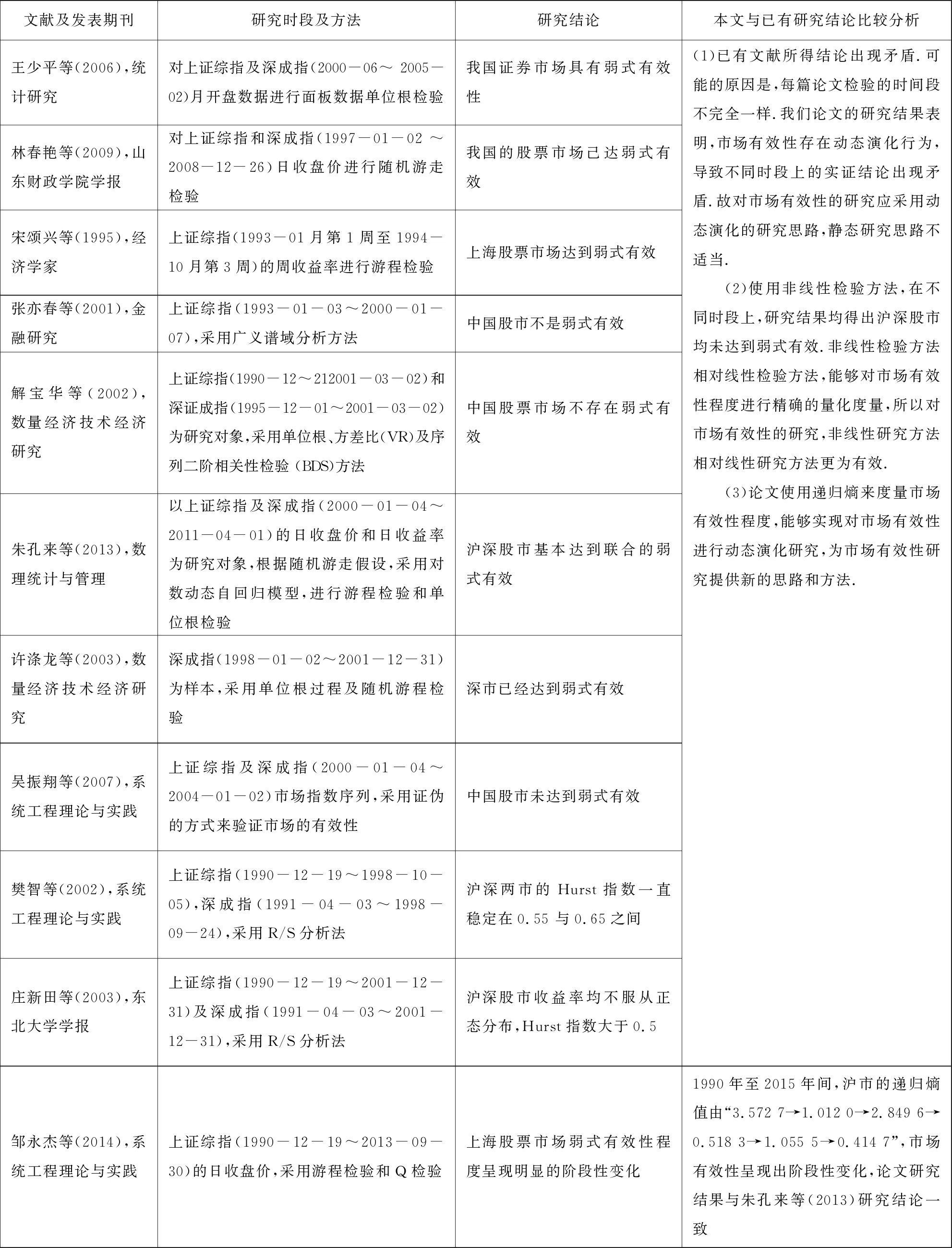
续表7

6 结束语

本文基于递归图方法和递归熵对股票市场有效性进行量化分析，通过对不同国家(地区)的股票市场有效性进行量化比较发现，市场有效性在不同时间尺度上表现出动态演化行为，并基于EMD+熵谱图的组合分析方法对股票市场有效性的动态演化规律进行分析，主要结论如下：

1)股票市场的有效性呈现出复杂的动态演化特征.在对股票市场有效性的研究中，普遍认为股票市场的有效性是由弱到强单向发展的，但本文通过对全球股票市场之间横向对比及每个市场在各阶段的纵向对比，分析得出股票市场的有效性呈现出复杂的动态演化现象，呈现出由“相对有效”——“相对无效”的反复波动中.进一步，本文使用最大熵谱估计方法对美国股票市场的有效性的周期性演化行为进行研究，发现在短时间内，美国股票市场的有效性存在两个周期(2.56年及4.57年).在低频率上既长时间段上，美国股票市场的有效性分别都只有一个周期，分别11.64年及25.60年，并且最大熵谱图都有十分锐利的单峰，说明周期性比较显著，且这些周期的Fisher 检验都通过显著性检验.

2)美国股票市场有效性的变动周期与基钦短经济周期、朱格拉经济周期及库涅茨经济周期中的经济周期吻合.在高频率上既短时间上.美国股票市场的有效性存在3年～5年的周期，这与基钦短周期经济理论中的3年～4年经济周期相吻合.在低频率上既长时间段上，美国股票市场的有效性存在约为11年的周期，这与1860年法国经济学家朱格拉提出的经济周期为10年左右的经济周期理论相吻合.在第五频率上既更长时间段上，美国股票市场的有效性存在约为25年的周期，这与1930年美国经济学家库涅茨提出的一种为期15年～25年的经济周期较为接近.这就产生了一个值得深入研究的问题，股票市场的有效性或许与经济周期之间存在某种关系，对这个问题的研究有助于获得对股票市场有效性更加深刻的认识，这也是进一步的研究方向.

3)社会环境的不稳定性及经济危机对市场有效性具负向效应.一个国家(地区)的社会动荡会影响到该国(地区)股票市场的有效性，比如法国社会在2017年～2018年出现动荡，该国股票市场的有效性程度急剧下降，在发生社会动荡之前法国股票市场的有效性程度相对较高.但最近三年，该国股票市场指数日收益率序列的递归熵达到2.755 3，市场有效性程度急剧下降.在最近十年间，墨西哥由于社会安全局势不断恶化催生政治变局，该国股票市场指数日收益率序列的递归熵由未发生社会动荡的0.517 0逐渐增加到2.580 0，股票市场有效性程度也出现急剧下降.但同时期，社会局势较为稳定的国家，股票市场的有效性表现较为平稳，未出现较大波动.通过分析2007年～2008年全球金融危机期间各国股票市场的有效性，发现危机期间各国股票市场的有效性普遍下降和出现剧烈波动.进一步分析1929年～1933年经济大萧条、1973年～1975年由石油危机引发的经济危机、1987年～1988年“黑色星期一”金融危机、1999年～2001年间的互联网投机泡沫这四次全球重大金融经济危机事件中美国股票市场的有效性，也发现各次危机期间股票市场的有效性普遍下降和出现剧烈波动，这表明金融危机对市场有效性具负向效应.

4)一般情况下，股票市场在成立之初的三年时间里有效性程度较低，但在随后六年时间里，随着市场法律规章制度的不断完善，各国股票市场的有效性程度将稳定在彼此互异的某一区间内波动.一般新兴市场国家(地区)由于在股市组建之初就能借鉴成熟资本市场的市场管理经验，所以在成立之初时市场的有效性程度一般要高于发达国家股票市场在成立之初时的有效性程度.比如在发达国家(地区)市场中，成立之初三年时间里比利时、奥地利、中国香港、德国、荷兰、英国、新加坡、新西兰股票市场指数的递归熵均大于2，而新兴市场国家(地区)墨西哥、韩国、以色列、中国台湾、印度、埃及和中国深市股票市场指数的递归熵均小于1.另外，股票市场的有效性呈现出时间尺度效应，一般情况下随着时间尺度的增大，市场有效性增强，如新西兰股票市场、韩国股票市场及美国股票市场等，但部分股票市场的有效性随着时间尺度的增大变弱，如澳大利亚股票市场、中国台湾股票市场.

5)通过使用层次聚类方法来综合分析各时间尺度下股票市场有效性的分类，比利时、瑞士、荷兰、中国沪市、奥地利及阿根廷股票市场的有效性较为接近，日本、新加坡、德国、韩国及马来西亚股票市场的有效性较为接近，中国香港、印度尼西亚、西班牙、印度股市有效性较为接近，美国、巴西及以色列股市的有效性较为接近，新西兰、埃及和法国股票市场的有效性较为接近，墨西哥、澳洲、英国及中国深市股票市场的有效呈现出不同于其它国家(地区)股票市场的有效性，表现出不同时间尺度下股票市场的有效性差异较大.