不同地震滑坡危险性评价方法的适用性探讨——以玛多MS7.4地震为例

魏延坤 陈晓利

(中国地震局地质研究所，活动构造与火山重点实验室，北京 100029)

0 引言

地震滑坡是坡体在地震作用下失稳而发生滑动的一种自然灾害现象。不同于降雨等因素诱发的滑坡，发生在山岳地区的强烈地震往往能够在较广范围内触发数量众多的滑坡；兼之地震滑坡的发生具有突发性和隐蔽性的特点，因而难以进行定点监测和预防(Keefer，1984；Chenetal.，2014；Tianetal.，2016；Xuetal.，2016；Raoetal.，2017)。已有经验表明，对于规模大、分布范围广的地震滑坡灾害问题，在土地利用的规划阶段就进行地震滑坡危险性预测和区划是行之有效的解决办法(许冲等，2011；陈晓利等，2013；王涛等，2015)。

对于区域性地震滑坡危险性的预测评估，前人的研究已取得了很多成果。例如，通过对世界范围内的地震滑坡震例进行统计，Keefer(1984)认为能够触发滑坡的最小地震震级为4.0级；而一次地震过程中，地震滑坡分布的范围与地震震级呈正相关，即S=f(M)，由此即可估计地震能够导致的滑坡范围(辛鸿博等，1999)，甚至可根据震级和滑坡数量的经验公式N=f(M)估算出滑坡的数量。然而，仅仅对滑坡的分布范围和数量进行估算并不能满足防灾减灾的实际需求，科学地预测地震滑坡发生的危险区域(甚至是灾害体规模)才能够对土地规划、工程项目选址以及社会经济的长远发展等起到预警和指导作用。

一般而言，滑坡预测主要分为时间和空间预测2个方面。其中，关于地震所导致的滑坡研究基本上是进行对空间的预测。现有的地震滑坡危险性预测和评价方法可分为2大类，即定性方法和定量方法。这2类方法在实际运用时所选择的分析模型是不同的。定性方法主要依赖经验模型进行滑坡预测，即通过对地震滑坡事件中滑坡的空间分布与影响因素关系进行研究以建立预测模型。其中，不同因素对滑坡形成的作用大小可通过多种分析方法获得。而定量方法则依据物理模型进行预测，该方法主要基于物体平衡原理，通过计算安全系数或位移判断边坡的稳定性。

总体而言，各种方法的出现在一定程度上反映了它们的有效性。但是，由于地震滑坡形成的复杂性，定性和定量方法在运用时都存在自身的局限性。定性方法之所以具有局限性，是由于其模型建立在对过去的地震滑坡分布和影响因素之间关系的基础上，这样的认识本身与具体的滑坡孕育环境密切相关，因此在将这种认识应用到一个新的区域前，需要对其通用性进行验证。定量方法所依赖的物理模型主要来自单个斜坡的预测研究，将其应用于区域地震滑坡稳定性评价中时，就会遇到测量资料不够精确的问题。

1 方法与数据

在地震滑坡问题的研究中，科学工作者发展出众多评价方法，其中Newmark模型是应用较为广泛的以物理模型为基础的方法。而在定性方法中，学者将更多的研究投入到滑坡影响因素的权重赋值上，判别分析法就是其中的一种。

图1 滑坡滑动体示意图(改自Jibson et al.，2000)Fig.1 Sliding-block model used for the Newmark analysis(adapted from Jibson et al.，2000).

1.1 Newmark模型

Newmark模型是Newmark(1965)在研究受到地震活动影响下的坝坡安全稳定性问题时提出的，其认为堤坝是否稳定主要取决于地震发生时坝坡累积位移量的大小。因此，坡体的变形程度与滑坡的发生密切相关。由于该模型具有较为严格的假设条件，与时程相关的参数不易获取，因此，Jibson等(2000)对其进行了一些简化，使之便于在区域范围的场景下推广。他们用斜面上的刚体移动来模拟滑坡过程(图1)，利用加速度数据获得滑块的位移。其中，临界加速度可用来衡量区域地震滑坡的易发性。临界加速度ac越大，能够承受的外力就越大，坡体就越稳定；反之，临界加速度ac越小，表示坡体越不稳定。

临界加速度ac表示为

ac=(Fs-1)gsinα

(1)

式(1)中，Fs为安全系数，α为坡体的坡角。

Fs可通过式(2)获得：

(2)

式中，c′为坡体物质的内凝聚力(MPa)，φ′为坡体物质的内摩擦角(°)，γ为物质的重力密度(kN/m3)，t是滑坡的厚度(m)，α为坡角(°)，m为坡体饱和程度，γw为水的密度(kg/m3)。

本文选择目前应用较为广泛的地震动峰值加速度(Peak Ground Acceleration，PGA)作为Newmark评估模型的地震动参数(Jibsonetal.，2000；Milesetal.，2000；Pradeletal.，2005；Rathjeetal.，2011；Dreyfusetal.，2013，陈晓利等，2019)。通过对比研究区的地震滑坡易发性(ac)与地震动峰值加速度(PGA)，可对研究区进行地震滑坡危险性的快速评估。PGA与临界加速度ac的差值越大，代表地震滑坡危险程度越高。图2 为基于简化Newmark位移模型的地震滑坡危险性快速评估的技术流程图。

图2 基于简化Newmark位移模型的地震滑坡危险性快速评估的技术流程图Fig.2 Structure based on simplified Newmark model.

1.2 判别分析法

众多研究表明，多种地貌、地质等因素对地震滑坡有影响(Keefer，1984；丁彦慧等，2000；Sassaetal.，2005；Wangetal.，2007；陈晓利等，2009)。根据这些因素对地震滑坡影响作用的不同，可将其分为内在因素和触发因素。内在因素指坡体本身的内在特征，包括坡体形态因素和坡体物质特征等；触发因素是使坡体破坏的外部因素，这里地震运动是触发因素。

虽然内在因素多种多样，但并非所有内在因素都与地震滑坡有着密切的关系。因此，选择合适的因素进行分析并确定各个因素的贡献率是非常重要的，这也是定性方法面临的一个核心问题。本文所用的判别分析法就是为了解决这一问题应运而生的。

图3 描述了这个方法的具体流程。这里，边坡坡度、平均曲率和地震动峰值加速度是本文选择的与地震滑坡关系最为密切的因素。式(3)为对2004年日本新潟地震滑坡进行分析获得的判别分析公式(陈晓利等，2010；Chenetal.，2014)。

F=0.079×I-35×C+0.018×A

(3)

其中，I为坡度(°)，C为曲率，A为地震动加速度(m/s2)，F为判别值。如果F≥0，则表明坡体失稳；若F<0，则表明坡体稳定。

图3 判别分析法的工作流程图Fig.3 Structure of the discrimination analysis method.

1.3 数据

上述2种方法需要的输入参数主要包括描述研究区地形地貌特点的坡度、曲率参数和描述研究区坡体物质特征的岩石力学参数，以及描述地震作用的地震动峰值加速度。

在本文的研究中，地形坡度数据由SRTM 30m数字高程模型(DEM)生成(图4)，并通过Arcgis获得曲率分布(图5)。坡体物质组成主要依据1︰20万地质图获得(图7)。由于缺乏具体地震台站的数据，计算所需的地震动峰值加速度则是根据应急管理部发布的青海玛多7.4级地震的烈度图进行转换获取(1)http：∥www.mem.gov.cn/xw/yjglbgzdt/202105/t20210528＿386251.shtml。(图6)。

图4 青海玛多 MS7.4 地震的区域坡度图Fig.4 Topographic slope map of Maduo earthquake afflicted area.

图5 青海玛多 MS7.4 地震震区的曲率图Fig.5 Topographic curvature map of Maduo earthquake afflicted area.

地震动峰值加速度(PGA)数据根据应急管理部发布的地震烈度图①以及中国地震烈度表(表1)(中华人民共和国国家标准编写组，2020)获得。由于无法获取研究区每个位置的地震动数据，本次研究利用ArcGIS空间分析功能使用反距离权重法(IDW，Inverse Distance Weighted)进行插值分析，以获得地震动峰值加速度分布图(图6)。

图6 玛多地震动峰值加速度分布图Fig.6 Peak ground acceleration map of the Maduo earthquake affected region.

图7 玛多地震研究区的岩性分组图Fig.7 Map showing distribution of rock formations.

表1 研究区烈度与PGA对应值(参考中国地震烈度表GB/T 17742-2020)Table 1 Corresponding values of intensity and peak ground acceleration in the study area

相对于地形坡度、地震动峰值加速度等参数，岩石力学参数的赋值则较为复杂。对于区域性问题的研究很难得到每处的岩石力学参数值，因此在研究时要对地质岩组进行分类赋值。

依据岩性相近的程度对玛多地震研究区域进行工程地质岩组分类，主要参考《工程岩体分级标准GB/T50218-94》(中华人民共和国国家标准编写组，1995)、《岩土工程勘察规范GB 50021-2001(2009年版)》(中华人民共和国建设部，2009)以及相关研究文献进行赋值(Jibsonetal.，2000；Dreyfusetal.，2013；Chenetal.，2014)。分类结果及各类参数如表2 所示，研究区的岩性分组如图7所示。

表2 玛多震区岩石力学参数Table 2 Rock parameters of Maduo earthquake afflicted area

2 结果

2.1 基于简化Newmark滑块模型计算的结果

根据式(1)，利用静态安全系数Fs和坡度数据得到玛多地震灾区的临界加速度ac分布图(图8)。

临界加速度ac可用来评估区域地震滑坡易发性，临界加速度ac越大，则坡体越稳定；反之，ac越小，则坡体越不稳定。从图中可以看出，滑坡易发性高的位置主要集中在Ⅵ度区NE侧坡度较陡的区域，但该易发性评估没有考虑到地震期间地震动对斜坡造成的影响，还需结合地震动数据PGA进行地震滑坡危险性评估。

图8 玛多地震震区斜坡的临界加速度ac分布图Fig.8 Map showing critical acceleration ac in Maduo earthquake afflicted area.

前文提到Newmark方法是基于物理模型的定量方法，但定量计算主要针对具体的边坡，将其应用于区域场景时，由于无法精确得到每处的参数，只能用相对危险程度描述结果(陈晓利等，2019)。针对所得结果，依据PGA与敏感性ac的差值大小对危险程度按照自然间断点(具有统计学意义的自然的转折点和断点，通过迭代比较每个分组和分组中元素的均值与观测值之间的平方差之和来寻找这些点，这些点可以把研究的对象分成性质相似的群组，并可使各个类之间的差异最大化)分级法进行分级(2)https：∥desktop.arcgis.com/zh-cn/arcmap/10.6/map/working-with-layers/classifying-numerical-fields-for-graduated-symbols.htm。，危险性由高到低分别为极高危险、较高危险、中度危险、较低危险和极低危险5个级别(图9)。

图9 基于简化Newmark方法的地震滑坡危险程度分级图Fig.9 Evaluation of coseismic landslide hazardous zones on Newmark analysis.

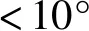
2.2 基于判别分析法的结果

根据判别分析公式(式3)，利用坡度、平均曲率和PGA数据得到F值，将计算结果按照表3 的分级标准分为5级，并计算各等级所占面积的比例(表3)，地震滑坡预测结果如图10 所示。

表3 玛多震区的地震滑坡危险程度分级Table 3 Classification of earthquake landslide danger degree

图10 基于判别分析法的地震滑坡评价图Fig.10 Evaluation map of seismic landslide based on discriminant analysis method.

结合表3 和图10 可以看出，在判别分析方法给出的结果中从高度危险至低度危险性级别所占面积的比例分别为6.89%、7.23%、5.31%、20.24%和60.33%，判别值F≥0的面积(即坡体不稳定面积)占研究区总面积的19.43%。与Newmark方法得到的结果不同的是，坡体不稳定区域在Ⅵ度区分布较广，受坡度曲率影响较大。

3 讨论

尽管截至本文成稿时仍未见玛多地震后有明显的地震滑坡报告，难以对这2种方法的准确性进行对照检验，但可以从理论上对2种方法所获得的结果进行比较，并对其适用性进行简要分析。

(1)从上述结果看，由于2种方法所采用的研究模型存在差异，在预测结果中不同危险程度的地震滑坡危险区分布并不一致，尤其是在Ⅵ烈度区中差异较大。从图9 可以看出，Newmark方法的结果中Ⅵ烈度区大部分范围为低度危险，而判别分析法在此区域得到的结果中约四分之一的区域处于高度危险级别，原因在于Ⅵ烈度区面积广、山区多、坡度起伏大，部分地区坡度较陡，将判别分析法用于此区域时受坡度和曲率值影响，得到的结果偏大；简化Newmark方法受地震动影响较大，而此区域远离震中，地震动的影响较弱，因此对此区域的主要预测结果为低危险级别。但2种方法在Ⅶ度区及以上研究区域整体的危险区划大体一致，预测效果较好。

(2)基于简化Newmark方法的地震滑坡危险性评估基于物体平衡原理，基本不受地震区域的地质背景条件限制，相对而言得到的结果更加真实。从结果中可以看出，地震滑坡的发生与地震动强度密切相关，整体上随着地震动强度的降低，滑坡发生的可能性也在降低，在这一方面，基于简化Newmark方法得到的结果与客观实际较为一致。但由于物理模型主要针对单体斜坡，推广到区域地震滑坡稳定性评价工作中时，无法得到精确的参数进行赋值，只能表述相对危险程度。本文基于Newmark模型方法对玛多地震进行了简单的评估分析，只考虑了坡体本身和地震动的影响，未考虑到水文、人类活动、地貌因素等条件的影响，同时Newmark评估方法需要获得较为明确的岩土物理力学性质及地震动参数，但在实际操作中很难获得每处坡体的准确数据，因此基于该模型的区域评估仍然存在缺陷和不足。与其他传统的以统计分析为基础的预测方法相比，该方法的物理意义更加明确，在与地震动参数的结合上具有其他方法不可替代的优势。

判别分析方法作为一种定性方法(或半定量方法)，采用的是由其他震例推导出的经验公式进行滑坡预测。而不同的地震区工程地质条件不同，对地震滑坡的控制因素也不一致，且各因素的影响权重存在一定差别。此次直接引用的式(3)是对2004年日本新潟地震滑坡进行分析所获得的，其更多地关注地貌条件(坡度、曲率)和地震动强度的影响。但新潟地震与玛多地震所处的地貌环境存在差异，因此取得的效果也不同。玛多地震震区的地貌条件与青藏高原东缘地区相比也有很大差异，即使采用由青藏高原东缘地区震例获得的滑坡预测模型进行预测也难以得到满意的效果。因此在区域范围场景下应用该方法时，要对所使用的经验公式的通用性进行验证，重新认识各个影响因子之间的关系，调整各因素的权重。

总体而言，从预测结果上可以看出，这2种方法在一定程度均可有效地预测区域地震滑坡危险性。但是，由于其考虑的影响因素不同且使用的约束条件较少，所得结果有一定差异。基于判别分析法对地震滑坡危险性进行评估时，需要充分分析客观完整的滑坡样本，这也是基于经验模型预测方法所面临的问题。而Newmark模型作为一种物理模型，尽管存在输入参数的准确度问题，但是它不依赖所处的具体环境，因而在计算结果上更为客观和合理。

4 结论

在区域性地震滑坡危险性预测研究中，无论是定性方法还是和定量方法，都有自己的优势和短板。实现对地震滑坡的精确预测还需要进行长时间的探索。本文采用简化Newmark模型方法和判别分析法方法分别对2021年发生于青海省果洛州玛多县的MS7.4 地震诱发滑坡的危险性进行了快速评估，获得如下认识：

(1)这2种方法在预测结果上的差异主要分布在Ⅵ度区，Ⅶ度区及以上研究区域，2种方法得到的危险区划大体一致，一定程度上反映了它们的有效性。

(2)以Newmark刚体滑移模型为基础，结合地震动峰值加速度对地震诱发滑坡危险性进行快速评估，得到的潜在高危险区域主要分布在Ⅷ、Ⅸ、Ⅹ烈度区，地震滑坡的发生与地震动强度密切相关，整体上，随着地震动强度的降低，滑坡发生的可能性也在降低。

(3)判别分析方法作为经验模型的一种，依赖于特定环境，在脱离本身固有环境使用时要对经验公式进行通用性验证，以重新认识各个因素的关系并分配权重大小。