带摩擦补偿的运动控制探索型实验设计

程国扬， 刘阳阳

(福州大学 电气工程与自动化学院，福州 350108)

0 引 言

摩擦现象在机械运动系统中普遍存在，它产生于存在相对运动(或趋势)的两个接触表面之间，起到阻碍运动的作用。摩擦力(或力矩)具有复杂的静态和动态特性，这给机电系统的精确运动控制带来了挑战。因此，对摩擦现象的数学建模和补偿控制成为机械工程和控制工程领域的共同研究课题[1-3]。

摩擦模型可以分为静态模型和动态模型两大类[4]。静态模型将摩擦力描述为相对速度的函数。目前常用的静态摩擦模型有库仑摩擦模型、库仑摩擦+黏滞模型、Stribeck摩擦模型、Karnopp摩擦模型等。当相对速度为零时，摩擦力依赖于外部作用力，此时称为静摩擦力;当外部作用力大于最大静摩擦力时，系统由静止开始运动，此时的摩擦力典型地会显著减小，这也是导致爬行现象和极限环的主要原因[5-6]。静态摩擦模型主要描述宏观的摩擦特性；而动态摩擦模型则可以进一步描述摩擦的微观动态特性，诸如摩擦记忆、滞环特性、预滑动位移等现象。目前动态摩擦模型研究较多的有Dahl模型、鬃毛模型、复位积分模型、LuGre模型[7-8]等。

摩擦的补偿控制也分为无模型补偿和基于模型的补偿。其中无模型补偿是把摩擦力当作是一种扰动，通过设计鲁棒控制器来消除或减弱扰动的影响[9]。基于模型的补偿则又细分为基于静态模型的补偿和基于动态模型的模型，其中前者通过事先或在线辨识一个静态模型的参数，并根据模型进行补偿控制。基于动态模型的补偿方法在理论上可以达到更好的控制效果，但由于动态模型的复杂性，其参数辨识比较困难，往往需借助自适应控制的方法来实现补偿[10]，而机电系统的动态特性较快，在其瞬态过程中难以确保自适应控制的参数收敛，所以实际应用起来有一定的难度。

本文针对工业中典型的伺服电动机运动系统，研究其位置跟踪控制和摩擦补偿问题。首先设计一个复合非线性控制器[11]，实现对给定轨迹的快速且平稳的跟踪；采用Stribeck模型对系统中存在的摩擦力矩进行建模与参数辨识；在轨迹跟踪控制器中加入摩擦补偿，得到最终的控制方案。接着在MATLAB中建立仿真模型，用于仿真分析；随后基于TMS320F28335数字信号处理器进行控制算法编程，在一台永磁同步电动机上进行实验研究。整个设计最终形成一个综合实验系统，用于支持本科生和研究生相关课程的实验教学[12-15]。

1 轨迹跟踪运动控制律设计

机电设备中伺服运动机构通常可用如下的数学模型来描述：

(1)

式中：y和v分别为被控系统的位置输出量(可量测)和速度;u为控制信号(转矩电流或输入电压);d代表由负载扰动、摩擦力矩和其他不确定因素折合而成的未知扰动;a≤0与b>0为系统参数。考虑到实际系统的限制，引入饱和限幅函数sat(·)，定义如下：

sat(u)=sign(u)·min{|>u|,umax}

(2)

式中：sign(·)为标准的符号函数；min{}表示取集合元素的最小值；umax为控制量的饱和限幅值。

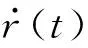
定义误差信号：

则有:

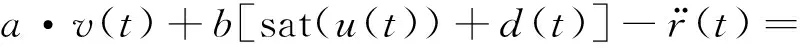
式中:

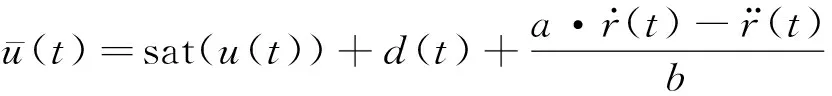
(3)

定义状态向量

则有:

(4)

式中，

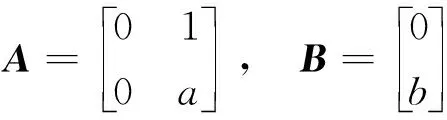
针对模型(4)，设计一个控制律，使e(t)→0。这里采用复合非线性控制技术[11]。这种控制技术可以突破线性控制技术的性能局限(即在给定带宽下快速响应与低超调不能得兼)，实现快速平稳且准确的轨迹跟踪。所设计的控制律如下：

(5)

设计非线性反馈控制律，来动态调节闭环阻尼系数。选取一个正定对角阵

求解Lyapunov方程

(A+BF)TP+P(A+BF)=-W

得到一个正定矩阵

则非线性反馈增益矩阵为

选取一个平滑的非线性增益函数

(6)

式中：α、β是非负的可调参数。ρ(e1(t))的绝对值随着跟踪误差e1(t)=y(t)-r(t)绝对值的增大而递减，如图1所示。这使得非线性反馈控制的强度可以动态调整。

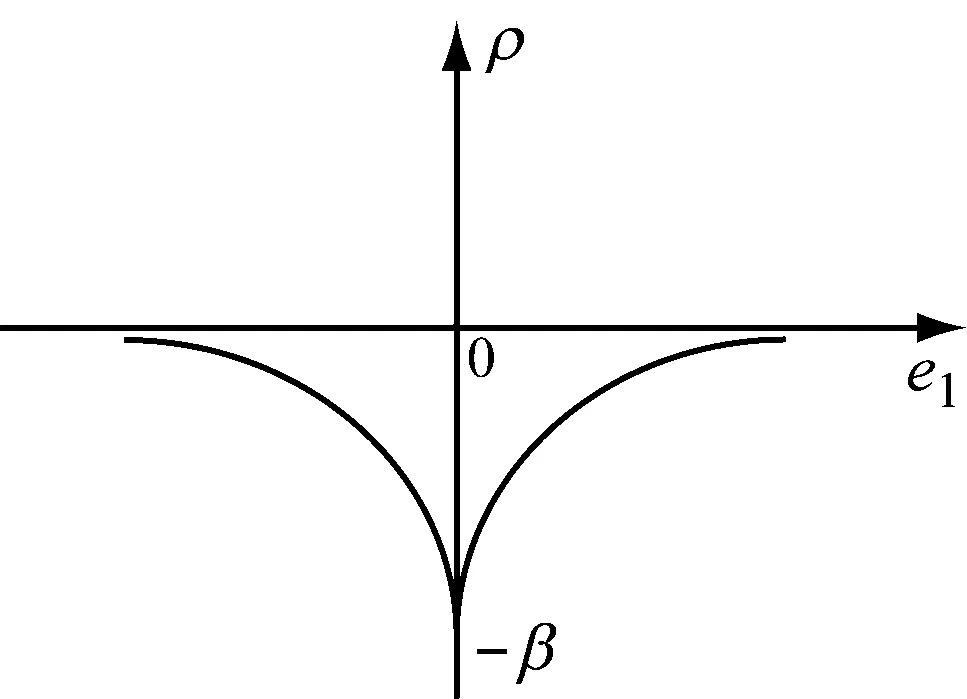
图1 非线性函数ρ(e)的示意图

根据式(3)，可解得系统(1)的跟踪控制信号(暂时忽略饱和限幅函数)为

(7)

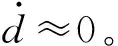
(8)

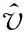
式中，ζ0∈(0,1]和ω0>0分别是观测器极点的阻尼系数与自然频率。基于观测器的跟踪控制律为

(9)

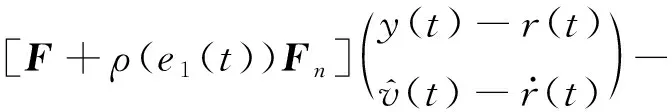
(10)

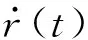
2 摩擦模型的辨识

针对伺服运动系统进行摩擦力矩的数学建模，采用如下的Stribeck模型：

Tf(v,Te)=

(11)

式中：

Tg(v)=[Tc+(Ts-Tc)e-(v/vs)2]sign(v)+σv

v为电动机速度(rad/s);Te为外作用力矩;Tc为库仑摩擦力矩;Ts为最大静摩擦力矩;vs为Stribeck速度;σ为黏滞摩擦系数。注意，式(11)中摩擦力矩Tf的表达式带有负号，是因为摩擦通常是阻碍运动的。

当系统运行稳定时，电磁转矩(扣除负载转矩后)与摩擦力矩的值是大小相等,方向相反的。因为电磁转矩与转矩电流成正比关系，所以当电动机匀速运动时，转矩电流之值可以表示摩擦力矩的大小。由于模型(1)把摩擦力矩和其他扰动都归入与控制信号(转矩电流)同一通道中，这里的摩擦力矩折算后成为等效电流，具有与电流相同的量纲，即采用安培(A)作为计量单位(等效值)。

对实验用的永磁同步电动机伺服系统进行速度闭环控制，使电动机做匀速运动，通过测量多组电流-速度数据，利用MATLAB软件的非线性拟合函数lsqcurvefit得到模型参数值:Tc=52.8 mA,Ts=191.5 mA,vs=8.613 8 rad/s,σ=0.2 mA·s/rad。

图2给出了拟合后的摩擦模型曲线(数据取正值)，其中只拟合了速度为正时的非线性曲线。速度为负时，所测量的数据基本与速度为正时的一致，只是符号相反，即曲线关于原点对称，故速度反向的拟合曲线在此处不再绘制。

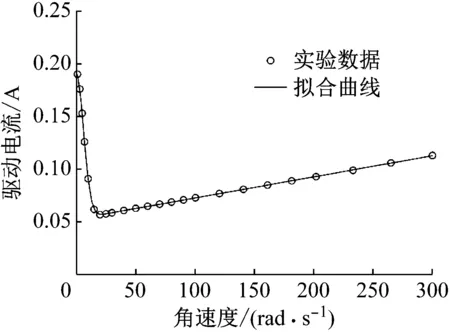
图2 转矩电流与角速度的拟合曲线

辨识的摩擦模型将用于仿真时的对象模型描述和摩擦补偿控制律。当摩擦模型用于描述对象特性时，其速度变量用真实的速度信号；而进行摩擦补偿时，只能用观测器估计的速度信号。

3 仿真分析

在MATLAB中搭建了轨迹跟踪控制系统的仿真模型，并进行仿真分析。针对式(1)所描述的伺服系统，采用系统辨识的方法得到其标称模型的参数值为：a=-10，b=1 950。根据设备的物理参数，确定umax=1.5 A，扰动d主要包含两部分：负载dL(等效值0～-0.8 A)，以及摩擦力矩Tf。

选取轨迹跟踪控制律的参数如下：ζc=0.3，ωc=30，α=10,β=2,ζ0=0.8，ω0=100。当采用不同的补偿控制方案时，系统的最终控制信号根据下式给出：

u(t)=

上述控制律可以统一表示为

(12)

式中：λ1和λ2为可调参数，它们都在区间[0,1]上取值，通过选取恰当的参数值，可以实现各种补偿控制方案，甚至可以只进行部分补偿，从而在控制精度和鲁棒性(对噪声的不敏感度)之间折中。这种参数化控制律为系统的灵活组态、编程实现以及性能优化带来了方便。

在给定正弦轨迹信号r(t)=2sin(2πt+π/3)和负载扰动dL=-0.5 A(近似为半载)情况下进行仿真，所得结果如图3～6所示。图中显示了给定轨迹与输出轨迹，估计的速度、负载、摩擦力矩，以及控制量(即转矩电流)。由图3可以看出，若控制律中无任何补偿(但仍继续对两种扰动进行估计)，则跟踪轨迹会产生很大的误差，并在峰顶和谷底出现了平顶现象(即爬行现象)，跟踪误差是由负载和摩擦共同作用造成的，而平顶现象主要是由摩擦导致的。由图4可以看出，加入负载补偿后，系统的跟踪性能有了很大的提升，但在轨迹的峰顶和谷底依旧存在轻微的平顶现象，这时的控制律把未补偿的摩擦力矩当成是负载来进行估计，但由于摩擦力矩是时变的，基于观测器(假设扰动为慢变化或定值)的补偿并不能完全消除摩擦所带来的不良影响，这也说明了对摩擦进行建模补偿的必要性。图5表明在对摩擦进行补偿之后，系统的输出轨迹比较平滑，不会出现平顶，但由于未补偿负载，轨迹跟踪出现了明显的误差。从图6可以看到，当控制律同时对负载和摩擦加以补偿时，轨迹跟踪非常准确，平顶现象已经消失，说明加入摩擦补偿起到了很好的补偿效果。这验证了在摩擦模型参数辨识足够精确的情况下，采用基于Stribeck摩擦模型反馈补偿的复合非线性控制方案可以在带有摩擦的伺服机构中实现准确的位置轨迹控制。

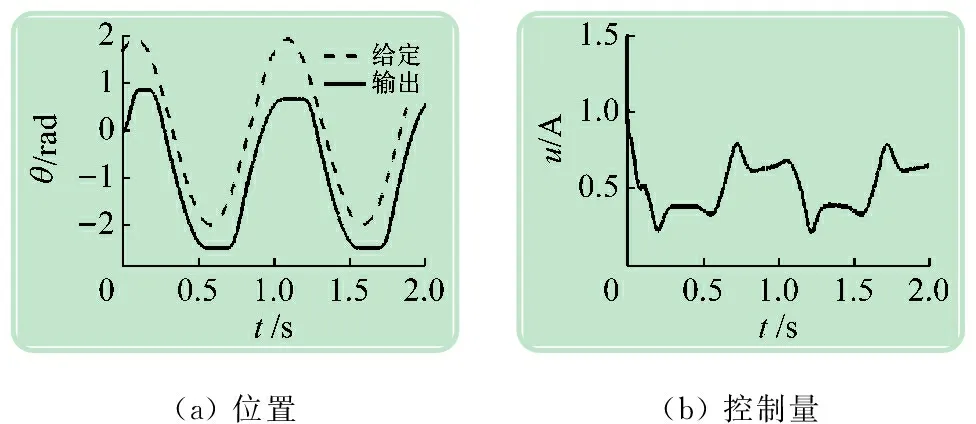
图3 无补偿时的仿真结果

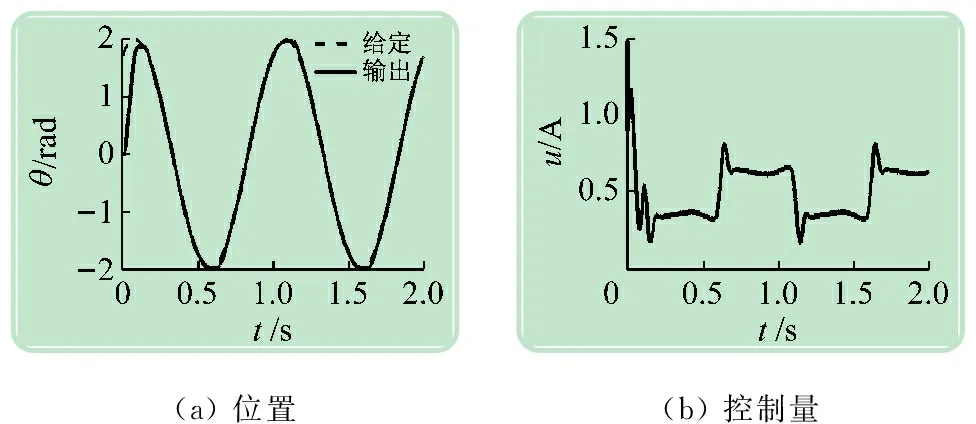
图4 仅补偿负载时的仿真结果

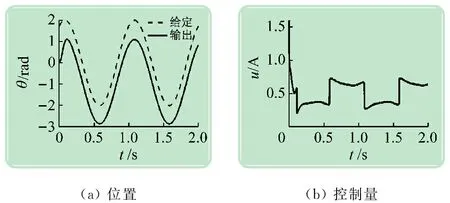
图5 仅补偿摩擦时的仿真结果

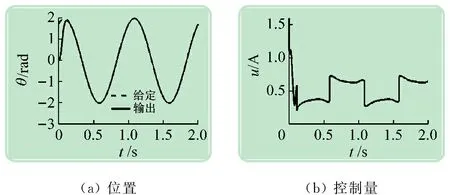
图6 同时补偿负载与摩擦时的仿真结果

4 实验测试

采用TMS320F28335为主控芯片，利用Code Composer Studio(CCS)软件，在一台永磁同步电动机(PMSM)试验台上进行了实时控制实验，如图7所示。电动机型号为60CB020C，其额定转速为3 000 r/min，额定转矩为0.64 N·m；带有2 500线的双路正交光电码盘，利用一个磁粉制动器来提供负载。电动机的电流内环已先行实现了闭环控制，电流环和脉宽调制的采样频率是20 kHz，位置环采用本文设计的控制律进行轨迹跟踪，其采样周期为Ts=2 ms。

图7 电动机运动控制实验台

实验中采用的控制参数值与仿真时相同。给定目标轨迹为正弦信号r(t)=π·sin(2πt+π/6)，该轨迹的周期为1 s。程序中使用4通道DLOG模块来采集数据，每个通道保存1 024个采样点。为了看到完整的正弦波以及轨迹跟踪的瞬态过程和稳态过程，在程序中设置一个方波信号，即当方波处于高电平时，让电动机跟踪目标轨迹；当方波处于低电平时，使电动机位置回零。设置高电平持续时间为750个采样周期，低电平为274个采样周期，则可以保证在1 024个采样点中，可以看到一个半周期的正弦波轨迹。

首先在20%负载的条件下进行实验，所得结果如图8～10所示。图8是控制律中无补偿时的实验结果，系统输出轨迹不但在峰顶和谷底有明显平顶现象，而且出现较大的误差；当控制律中加入负载补偿后，轨迹跟踪性能明显改善(见图9)，除了在峰顶和谷底时有较轻的平顶现象外，基本实现了准确的轨迹跟踪；如图10所示，当同时进行负载和摩擦补偿时，输出轨迹的峰顶和谷底变得更加平滑，能够较好地跟踪目标轨迹，说明摩擦补偿起到较好的补偿效果。图11是在60%负载下同时进行负载和摩擦补偿的轨迹跟踪实验结果，可以看到系统基本能平滑地跟踪目标轨迹，但在靠近峰顶和谷底的位置，仍有肉眼可见的跟踪误差。这可能是因为摩擦模型辨识得不够准确，以及系统中带有时变不确定性，无法完全通过观测器准确估计出来用于补偿。图12给出了在60%负载下对定点目标π的跟踪控制结果，系统实现了快速且低超调的跟踪性能，稳态误差可忽略。实验中也发现，在定点跟踪控制时，采用负载补偿已经可达到较理想的性能，再加入摩擦补偿后性能改善并不明显，这一点与曲线轨迹跟踪时的情形有所不同，这是因为曲线轨迹跟踪时系统会周期性地出现速度过零的位置，而在低速区域摩擦力矩的影响较大，所以相应地摩擦补偿的效果也较为明显。

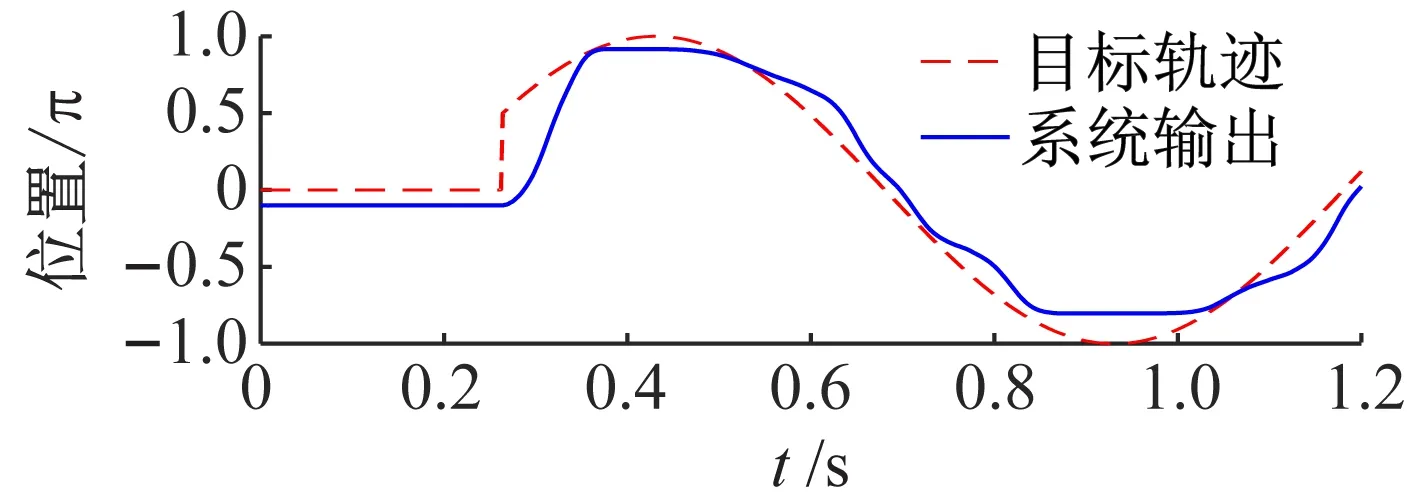
图8 负载20%下无任何补偿的实验结果

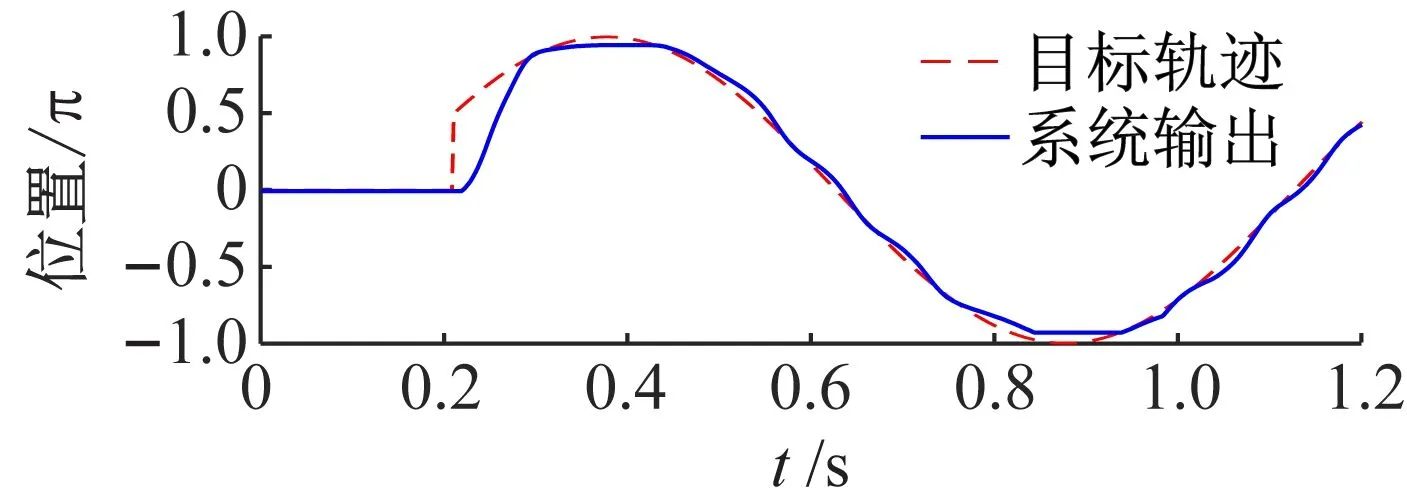
图9 负载20%下仅补偿负载时的实验结果

图10 负载20%下同时补偿负载与摩擦时的实验结果

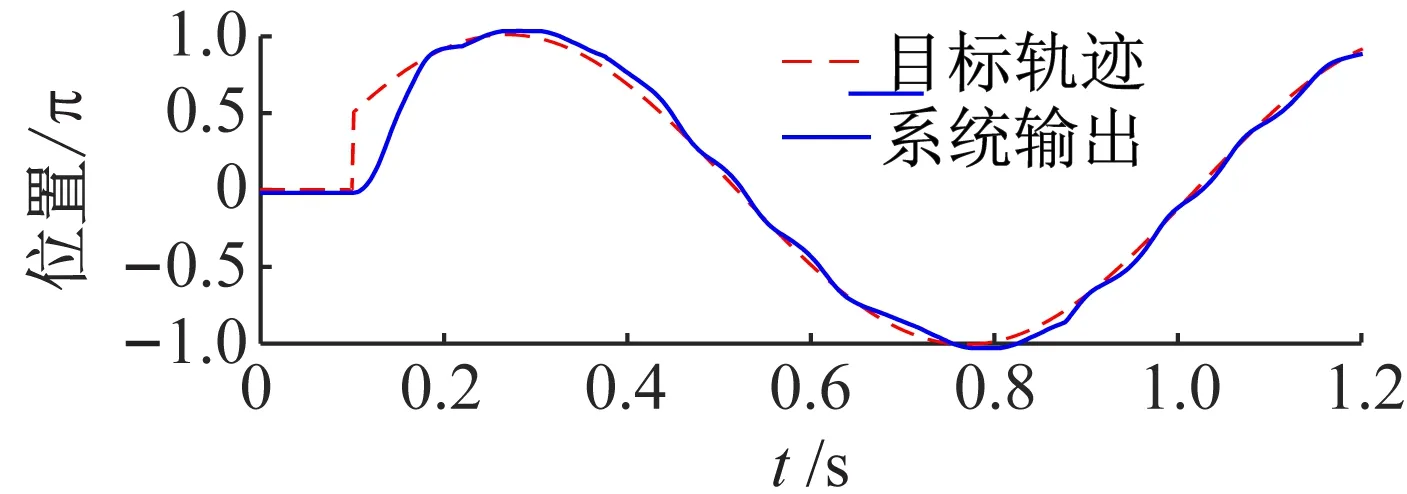
图11 负载60%下同时补偿负载与摩擦时的轨迹跟踪实验结果

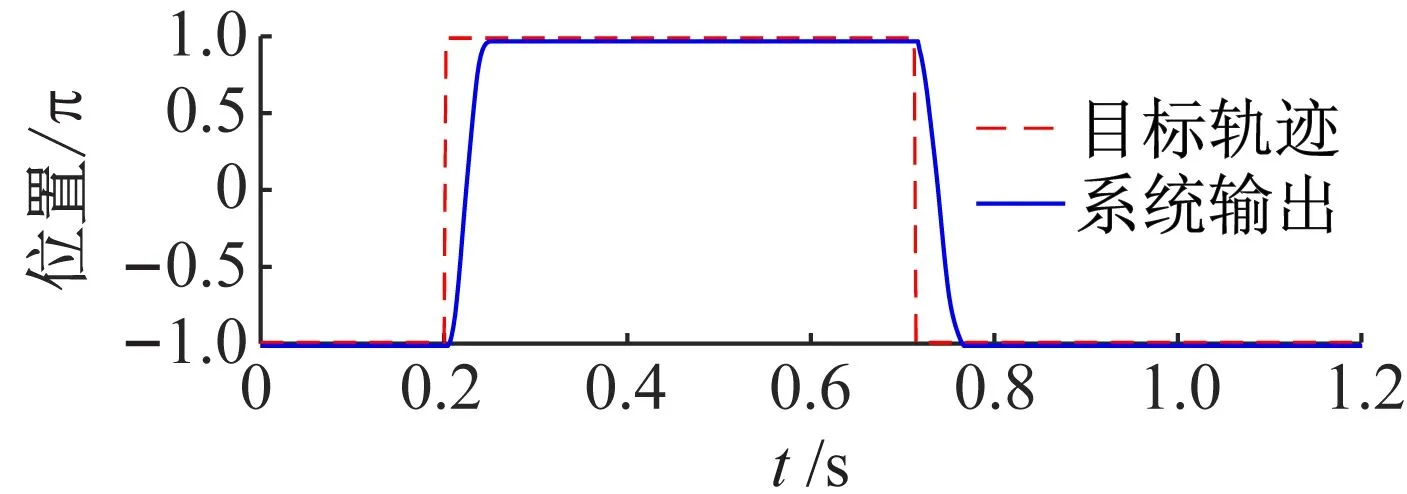
图12 负载60%下同时补偿负载与摩擦的定点跟踪实验结果

5 结 语

针对伺服运动机构设计了一种轨迹跟踪控制器，采用基于扩展状态观测器的线性与非线性控制相结合的方案，消除负载扰动和其他不确定性带来的影响；通过对摩擦力矩的数学建模，在轨迹控制律中加入摩擦补偿作用，最终实现准确的轨迹跟踪。进行MATLAB数值仿真和基于DSC芯片的实时控制，测试比较了各种补偿控制方案的性能。实验应用到本科生的运动控制系统实训和研究生的伺服工程科研实践环节，帮助学生掌握轨迹跟踪控制方法和摩擦建模与补偿技术。今后，我们还将融入参数自校正、学习控制、性能预测等手段，实现高精度伺服控制，并推广应用于工业领域。