改进的减轮Kiasu-BC 算法的中间相遇攻击
李曼曼,陈少真
(1.信息工程大学网络空间安全学院,河南 郑州 450001;2.密码科学技术国家重点实验室,北京 100878;3.河南省网络密码技术重点实验室,河南 郑州 450001)
0 引言
随着高新技术的飞速发展,以及网络支付系统、云计算、物联网技术的日益成熟,人们对隐私保护及信息安全等相关问题越来越重视。分组密码由于其软硬件实现效率高、易于标准化等优点被广泛用于保护信息的安全。可调分组密码是一种带有额外输入调柄值的分组密码,调柄值可以提高算法的灵活性,在构造Hash 函数、消息认证码和伪随机数发生器等领域应用广泛。近些年,可调分组密码迅速发展,其设计方法与安全性分析得到人们诸多关注和研究。在CRYPTO 2002 上,Liskov 等[1]提出了可调分组密码的概念。与传统的分组密码相比,可调分组密码有一个额外的输入调柄,这是一个完全公开的参数,增加了分组密码的可变性。在实际使用过程中,更换调柄比更换密钥操作更便捷有效且成本低廉。因此,可调分组密码被广泛应用于加密协议、认证加密等场合,以保护数据的机密性和认证性。
Jean 等[2]在ASIACRYPT 2014 上提出了一个可用来设计可调分组密码的简单框架——可调密钥(Tweakey)模型,并给出了3 个基于AES 算法轮函数的可调分组密码的具体实例,分别是Kiasu-BC[3]、Joltik-BC[4]和Deoxys-BC[5]。近几年,针对Kiasu-BC算法的安全性分析,研究者使用多种密码分析方法给出了较好的分析结果。最初,Kiasu-BC 算法的设计者分析了Kiasu-BC 算法的中间相遇攻击和差分攻击,并且声称Kiasu-BC 算法与AES-128 算法持有相同的轮函数和密钥扩展算法,故其抵抗密码分析方法的能力与AES-128 算法相同。
之后,研究者对Kiasu-BC 算法安全性分析的主要结果如下。Dobraunig 等[6]利用调柄自由度构造了4 轮区分器,实现了7 轮Kiasu-BC 算法的积分攻击;Abdelkhalek 等[7]利用调柄生成的差分可抵消攻击路径的差分首次构造了 8 轮Kiasu-BC 算法的不可能差分攻击;Tolba 等[8]利用调柄差分增加区分器轮数实现了8 轮Kiasu-BC算法的中间相遇攻击;Dobraunig 等[9]对 8 轮Kiasu-BC 算法的不可能差分攻击进行了改进,并提出了8 轮Kiasu-BC 算法的飞去来器攻击;Jiang等[10]借鉴调柄生成的非零差分抵消攻击路径差分的思想,提出了8 轮Kiasu-BC 算法的多重不可能差分攻击。
本文主要研究Kiasu-BC 算法的中间相遇攻击。Kiasu-BC 算法的中间相遇攻击最初由Jean 等[3]提出。Tolba 等[8]利用Kiasu-BC 算法的调柄差分性质,通过控制调柄差分使区分器在其第一轮处差分为0,据此将区分器的轮数扩展到5 轮,在构造区分器的前面增加一轮、后面增加2 轮,实现了8 轮中间相遇攻击。Liu 等[11]结合差分枚举技术选取不同于文献[9]的活动字节对中间相遇区分器进行了改进,更新了8 轮中间相遇攻击的结果,降低了Kiasu-BC 算法中间相遇攻击的时间复杂度和数据复杂度。关于Kiasu-BC 算法的中间相遇攻击,本文在前人研究的基础上,结合Kiasu-BC 算法的性质,寻找其密钥扩展算法的特点,发现Kiasu-BC算法内部密钥间的关联性,利用Kiasu-BC 算法密钥扩展的缺陷和轮变换的特点,构造一个新的5 轮中间相遇区分器,然后利用该区分器,向前扩展一轮、向后扩展2 轮,改进了8 轮Kiasu-BC 算法中间相遇攻击的结果。改进后的8 轮Kiasu-BC 算法中间相遇攻击的存储复杂度为263,时间复杂度为2114,数据复杂度为2108。
1 预备知识
1.1 符号说明
本文用到的符号说明如表1 所示。

表1 符号说明
1.2 Kiasu-BC 算法介绍
Kiasu-BC 算法是在AES-128 算法的基础上设计的可调分组密码算法,采用代换−置换网络(SPN,substitution-permutation network)结构,明文分组长度和密钥长度均为128 bit,加密轮数为10 轮。Kiasu-BC 算法的结构如图1 所示。Kiasu-BC 算法中调柄T的结构如图2 所示。
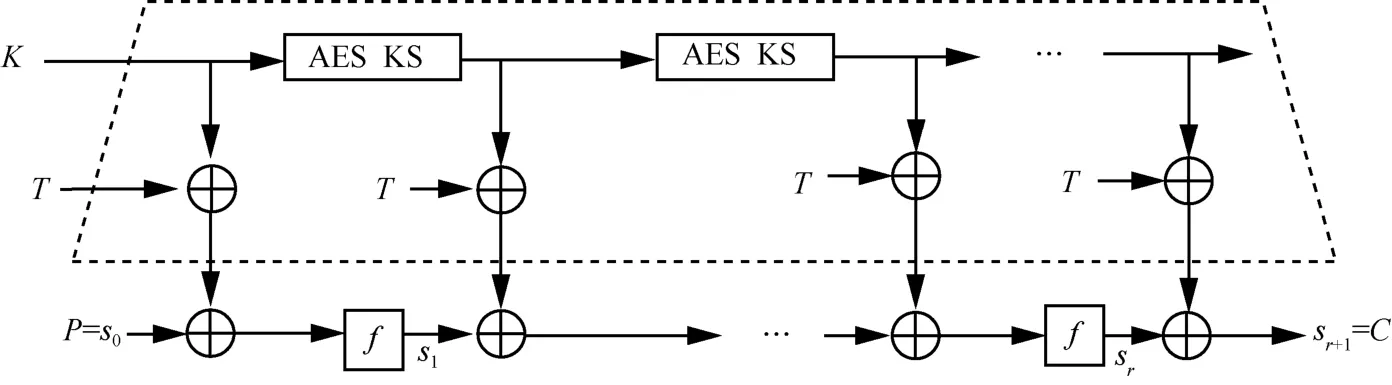
图1 Kiasu-BC 算法的结构
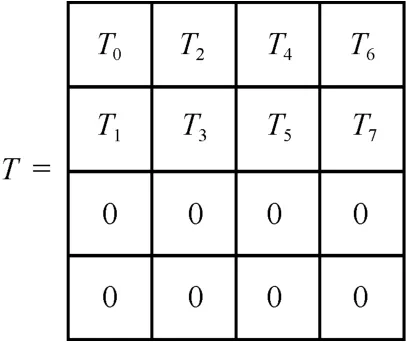
图2 调柄T的结构
Kiasu-BC 算法的128 bit 明密文及中间状态可分成16 块,表示为如下的4 × 4字节矩阵,每个字节可以看作 GF(28)中的一个元素。

Kiasu-BC 算法的轮函数与AES-128 算法相似,分别由字节替换(SB,SubByte)、行位移(SR,ShiftRow)、列混合(MC,MixColumn)和轮调柄密钥加(ART,AddRoundTweakey)4 种变换构成,其中前3 种变换与AES-128 算法相同,ART 变换就是将192 bit 轮调柄密钥STKi与128 bit 中间状态进行按位异或运算。其中,192 bit 轮调柄密钥由128 bit轮密钥RKi和64 bit 调柄T级联而成。Kiasu-BC 算法的轮调柄密钥生成如图3 所示。
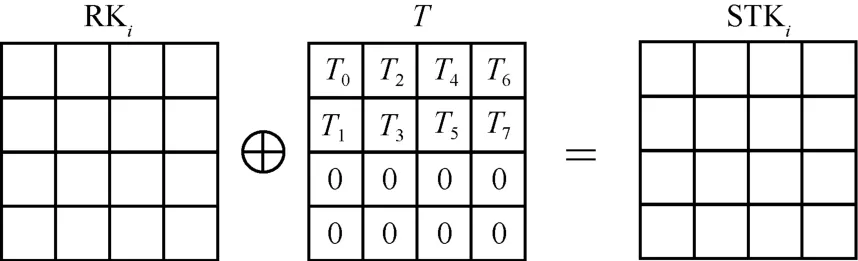
图3 Kiasu-BC 算法的轮调柄密钥生成
另外,在Kiasu-BC 算法的128 bit 明文进入轮函数之前,需要先进行一个白化的轮调柄密钥加变换,并且最后一轮的列混合变换被省略。
Kiasu-BC算法128 bit轮密钥RKi是由AES-128的密钥扩展算法得到的,对初始密钥进行扩展并将其分配到加密过程的每一轮。
2 中间相遇攻击
中间相遇攻击是一种有效的选择明文攻击,由Diffie和Hellman[12]于1977 年分析DES 算法时提出,该攻击方法利用密码分割和时空折中2 种分析思想,在分组密码和Hash 函数的安全性分析中均有广泛应用。随着20 世纪90 年代差分攻击的出现,许多密码分析方法逐渐融合形成新的、有效的分析思想。例如,不可能差分攻击就是利用截断差分在中间相遇产生矛盾的思想提出的,其本质也是中间相遇攻击。目前,研究者利用中间相遇攻击对许多分组密码算法进行了有效分析。在过去几年里,这种攻击方法被改进成一种名为原像攻击的方法,然后应用于Hash 函数的攻击中,并据此提出许多新的技术。
2008 年,Demirci和Selcuk[13]在分析AES 算法安全性的过程中,将碰撞攻击的思想[14]与中间相遇攻击相结合,提出了一种新型的中间相遇攻击模型,称为Demirci-Selcuk 中间相遇攻击。其基本思想是将一个分组密码算法E分割成连续的3 个部分,即E=E2◦E0◦E1,如图4 所示。
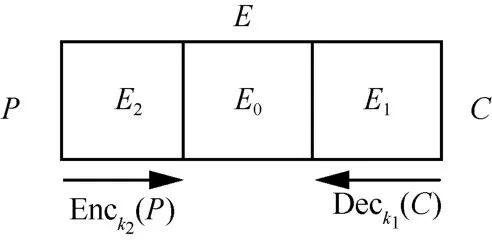
图4 Demirci-Selcuk 中间相遇攻击的基本思想
攻击过程包含离线部分和在线部分。在离线部分E0处,构造一个中间相遇区分器,用一个预计算表存储区分器中特定的输入和输出;在密钥恢复阶段即在线部分,猜测E1、E2的某些相关子密钥k1、k2,加密选择明文,同时解密对应的密文,检测得到的值与预计算表中存储的值是否相匹配。如果匹配,那么猜测密钥是正确的;如果不匹配,那么猜测密钥是错误的,因此排除这个错误的猜测密钥。
Dunkelman、Keller和Shamir[15]在2010 年提出了差分枚举技术,用来解决Demirci-Selcuk 中间相遇攻击存储复杂度较大的问题,同时提出密钥桥技术,通过寻找密钥间的制约关系,降低攻击的时间复杂度。在2010 年亚密会分析AES 算法时,Dunkelman、Keller和Shamir 在Demirci思想的基础上引入多重集并利用有效的差分枚举手段,大大降低了中间相遇攻击预计算阶段的复杂度。2013 年,Derbez 等[16]利用反射攻击的思想对差分枚举技术进行了改进,利用改进后的差分枚举技术可以进一步降低Demirci-Selcuk 中间相遇攻击的存储复杂度。
Li 等[17]在2015 年提出相关密钥筛选技术,结合差分枚举技术可以进一步控制内部状态的取值范围,降低Demirci-Selcuk 中间相遇攻击的存储复杂度。随后,Demirci-Selcuk 中间相遇攻击技术被用于分析各种类型的分组密码算法[18-21]。
在CRYPTO 2016 上,Derbez和Fouque[22]总结梳理了Demirci-Selcuk 中间相遇攻击的攻击模式,利用计算机语言将Demirci-Selcuk 中间相遇攻击的攻击流程进行转化,实现了Demirci-Selcuk中间相遇攻击的自动化搜索。借助计算机强大的计算能力,搜索最优的Demirci-Selcuk 中间相遇攻击方案。
上述关于中间相遇攻击的改进技巧或方法为人们今后的研究提供了理论支撑,利用差分枚举、密钥桥等技术可以优化攻击结果。中间相遇攻击的自动化研究也是目前的一个研究热点,针对具体的算法给出自动化搜索的结果,这也是本文将要深入研究的一个问题。
3 Kiasu-BC 算法的5 轮中间相遇区分器
本节进一步研究密钥扩展算法存在的缺陷,挖掘轮密钥间的相互制约关系,构造了一个新的Kiasu-BC算法5轮中间相遇区分器。在分析过程中,本文明确区分轮密钥和调柄,第i轮的轮密钥记作第i轮的调柄记作
3.1 Kiasu-BC 算法的性质
从密钥扩展算法可知,Kiasu-BC 算法每轮的最后一个变换所需要的轮密钥是由初始密钥经过扩展得到的。从上面描述的密钥扩展方案,本文可以得到下面的关系。

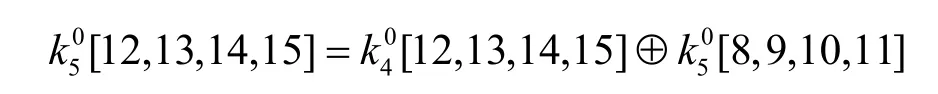
在攻击过程中,本文还会用到下列定义和性质。
定义1[23]算法的b-δ-集是由其2b个中间状态构成的集合,且这2b个中间状态在某一个字节(活跃字节)处遍历,在其余字节(不活跃字节)处固定。
性质1[24]给定任意一个双射S 盒S,Δi和Δo分别为随机选取的非零输入差分和非零输出差分,则方程平均只有一个解。
3.2 构造5 轮中间相遇区分器
本节考虑w0[0]是活跃字节,经过5 轮Kiasu-BC算法加密后,可以计算出相应的有序序列Δx6[0,1]。本文充分考虑密钥扩展算法产生的轮密钥间的制约关系,提出新的Kiasu-BC 算法的5 轮中间相遇区分器,得到定理1。




这样,就用一个5 bit 参数和11 个字节推出了第一步中的字节参数。
为了确保分析工作的严谨性,一般在选择δ-集时,如果对于4×4状态矩阵的每一块是8 bit的算法,可选择5-δ-集;如果对于4×4 状态矩阵的每一块是4 bit的算法,可选择4-δ-集。选择不同的δ-集对数据复杂度的影响比较小。本文的主要工作是发掘密钥间的制约关系来降低存储复杂度,给出截断差分特征的定理描述并进行详细证明。在此基础上,构造Kiasu-BC 算法新的5 轮中间相遇区分器,继而实现Kiasu-BC 算法的8 轮中间相遇攻击。
4 改进的8轮Kiasu-BC算法的中间相遇攻击
在一些情况下,为了降低攻击的复杂度,需要交换列混合变换与轮调柄密钥加变换的顺序。因为这2 个变换都是线性的,可以直接交换它们的顺序,同时参与异或运算的轮密钥相应地变为研究密钥扩展算法产生的轮密钥间的制约关系,利用内部密钥间的关系减少区分器中涉及的有序序列的取值个数,构造5 轮中间相遇区分器,在区分器的前面加一轮、后面加2 轮,实现对8 轮Kiasu-BC 算法进行中间相遇攻击,具体如图5 所示。改进后的8 轮Kiasu-BC 算法中间相遇攻击的时间复杂度为2114,存储复杂度为263,数据复杂度为2108。
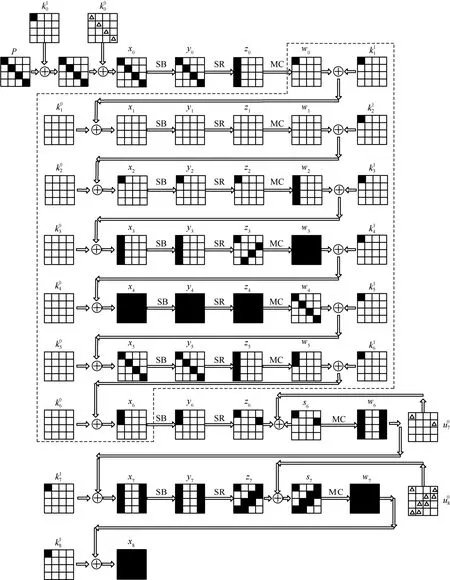
图5 8 轮Kiasu-BC 算法中间相遇攻击路径
4.1 Kiasu-BC 算法的8 轮攻击过程
攻击过程可以分为预计算阶段(线下部分)和在线阶段(线上部分)2 个阶段。
在线阶段。首先需要找到一对满足图5 所示的截断差分特征的明文。然后构造包含该明文对的5-δ-集,计算对应的有序序列。最后检测计算的序列是否存在于哈希表H中。攻击的过程描述如下。
1) 首先定义一个明文集在(0,5,10,15)处遍历,在其他12 个字节处固定,该集合由 232个明文组成。其次定义一个调柄集合在T[0]的前5 bit 遍历,其余字节处固定,集合由25个调柄组成。利用这2个集合可以得到24×8+5=237个密钥调柄组合,进而可得到 237× (237− 1) ÷ 2 ≈ 273个满足图5 所示的截断差分特征的明文差分对。2) 截断差分特征的概率为 2−(3+1+8+6)×8=2−144,需要选取 2144−73=271个明文结构,因此共有明文−调柄组合 271+37=2108个。
3) 查询结构中每个明文−调柄组合所对应的密文,并对其进行部分解密,得到s7的值,且满足每一个消息对在s7[1,2,3,4,8,11,14,15]处的差分为0。满足上面条件的消息对有 2144−8×8=280对,对 280个消息对中的每一个执行以下步骤。


4.2 复杂度分析
攻击复杂度的分析过程如下。
预计算阶段。每个有序序列有3 1×1 6=496 ≈ 29bit,大约需要 261× 29÷ 128=263个128 bit 块的存储空间。对5-δ-集进行部分加密,约等价于1.5 轮Kiasu-BC 加密运算,因此预计算阶段的时间 复杂度 为 261× 25× 1.5 ÷ 9 ≈ 263.6次 8 轮Kiasu-BC 加密。
在线阶段。时间复杂度主要由4.1 节步骤3) 决定,对32 个值的计算过程约等价于一轮Kiasu-BC加密运算,时间复杂度为 280× 232× 25× 1 ÷ 8=2114次8 轮 Kiasu-BC 加密。攻击所需的数据量为个选择明文。
综上可得,该攻击的时间复杂度为预计算阶段时间复杂度与在线阶段时间复杂度之和,约为 2114,存储复杂度为263,数据复杂度为2108。
因此,改进后的中间相遇攻击时间复杂度为2114次8 轮Kiasu-BC 算法加密,存储复杂度为263个128 bit 块,数据复杂度为 2108个明文−调柄组合。
表2将本文对Kiasu-BC 算法的攻击结果与其他中间相遇攻击结果进行了对比。

表2 Kiasu-BC 算法与其他中间相遇攻击结果的比较
与文献[8]的工作相比,本文工作主要是纠正了文献[8]的中间相遇攻击中所用到的截断差分特征的概率,并基于密钥扩展算法探寻Kiasu-BC 算法轮密钥间的关系,利用密钥间制约关系改进中间相遇结果,大大降低了存储复杂度;与文献[11]的工作相比,本文充分考虑算法自身的密钥相关性,降低了攻击过程的存储复杂度,同时可以启发有兴趣的研究者深度发掘更多的密钥相关性,利用密钥桥等技术改进现有的攻击结果。深度发掘Kiasu-BC 算法的密钥间关系,也可以为其他的攻击方法提供更好的改进思路,例如Kiasu-BC 算法的不可能差分攻击。
5 结束语
本文主要研究了Kiasu-BC 算法的中间相遇攻击。通过研究Kiasu-BC的密钥扩展算法,利用调柄自由度以及内部密钥间的制约关系,结合Kiasu-BC 算法轮变换中的线性关系,提出了新的5 轮中间相遇区分器,降低了存储复杂度,对8 轮Kiasu-BC 算法中间相遇攻击的现有结果进行了优化。改进后的8 轮Kiasu-BC 算法中间相遇攻击的时间复杂度为2114,存储复杂度为263,数据复杂度为2108。
如何构造较长轮数的中间相遇区分器,是笔者进一步研究的方向;将中间相遇攻击与其他攻击方法相结合,实现更多轮数的攻击路径,从而得到更有效的分析结果,也是笔者将要研究的工作。

