指数Gamma分布在无资料地区水文频率分析中的应用研究

李 航，易瑞来，廖朴讷

(广州市增城区中新镇人民政府，广州 511365)

1 概述

随着我国水利事业的蓬勃发展，目前国内水利工程的建设重心已经从大型水利工程向中小型水利工程转移，而城市化进程的飞速推进、城市防洪排涝体系的不完善和城市布局的不合理，越发凸显城市中小型水利工程配套建设的落后。水文频率分析是根据区域内的某种水文现象的统计特征，利用现有水文数据资料，分析和计算水文变量设计值与重现期之间的定量关系，是水利工程规划、设计与管理的基础和科学依据，分析结果的精确与否将会直接关系到流域水利工程是否能够发挥其应有的作用[1]。然而，中小流域作为近年来水利工程的建设重心，常常会因为自然条件和人为因素的限制，出现无法取得基础性水文数据的状况，为水资源的科学管理和水利工程的规划建设造成很大困扰。根据世界气象组织的统计数据，最近20年间，世界上的水文站点数量正在迅速减少，尤其是前苏联和一些发展中国家，作为最大的发展中国家，中国现有的设站条件面临着同样的难题[2]。

为解决无资料地区的水文频率分析和水文预报问题，促进水文科学理论研究和技术研究应用于解决实际性问题，2003年7月国际水文科学学会(IAHS)正式启动无资料地区水文预测计划，即PUB计划(Prediction in Ungauged Basins)[3]。经过十几年的研究对比，目前常用的无资料地区水文频率分析和水文预报的方法可以大致分为四类：随机模拟法[4-6]、区域化方法[7-8]、径流系数法[9-10]和参数等值线图法[11]，分别适用于不同资料缺失程度的研究区域。在工程所在流域找不到参证流域且无降雨资料的情况下，参数等值线图可以根据已绘制的各省市水文特征等值线图经过计算得到设计年径流量[12]。因此，参数等值线图法成为中小流域水利工程建设过程中实际应用最多的方法。

目前，参数等值线图法中最为常用的水文频率计算模型为皮尔逊Ⅲ型分布。然而，皮尔逊Ⅲ型分布并不能适用于各种自然条件，且近年来随着水文极值的不断出现[13]，在水文频率分析过程中时常出现皮尔逊Ⅲ型分布与经验点据明显脱离的不合理现象[14]。为了提高水文频率分析模型的适用性和弹性，同时兼容现有皮尔逊Ⅲ型分布的设计标准，1985年，中国水利水电科学研究院孙济良先生等[15]提出指数Gamma分布模型，该模型可以通过改变参数转化为包括P-Ⅲ型分布、对数正态分布在内的10余种常见分布模型。

受限于当时的计算机技术及模型计算方法，具有4个参数的指数Gamma分布参数估计计算较为复杂，因此并没有得到广泛的应用。随着计算机的广泛应用和模型方法的研究，指数Gamma分布优秀的拟合效果和适用性得到越来越多水文学者的关注。

在我国现有条件下，基层水文工作缺乏足够技术力量支持，水文测站无法短时间内在全国范围内普及。在缺少技术力量和水文资料的情况下，将指数Gamma分布应用于参数等值线图法，并开发配套的水文设计值计算工具，能够免去筛选合适拟合曲线的繁琐过程，有效解决各种水文自然条件下无资料地区的水文频率分析问题，并提高水文设计值计算精度。

本文选取江谷河流域作为研究区域，以指数Gamma分布作为频率分布曲线，通过广东省水文局颁布的《广东省暴雨参数等值线图》(2003年版)采用参数等值线图法进行水文频率分析，得出暴雨设计值与采用优化适线法的指数Gamma分布计算结果和采用参数等值线图法的P-Ⅲ型分布计算结果进行对比研究，分析指数Gamma分布在无资料地区的水文频率分析结果的可靠性。文中分析结果以期为我国无资料地区水文频率分析的研究和应用提供支撑。

2 指数Gamma分布的参数估计方法

设随机变量X服从指数Gamma分布，其概率密度函数为：

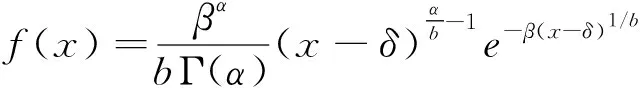
(1)

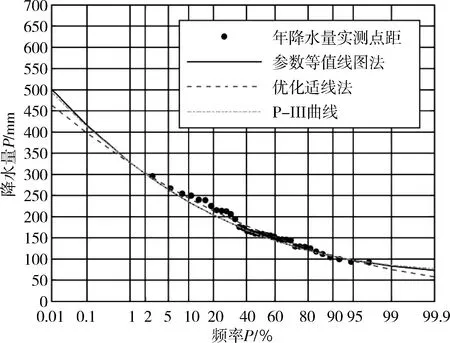
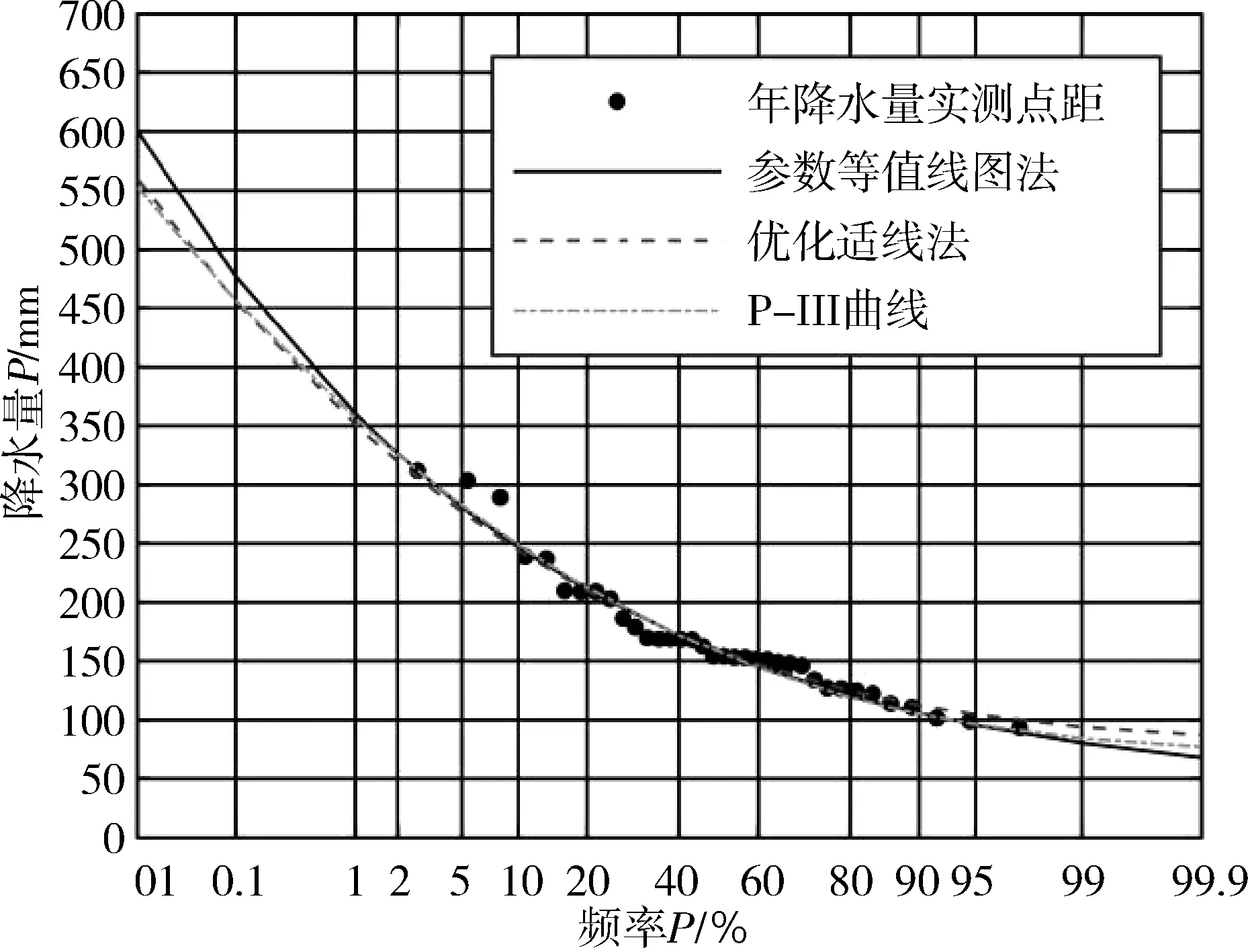
α>0,β>0,δ

式中：

α，b，β，δ——分别为指数Gamma分布的形状参数、变换参数、比例参数和位置参数。

变换参数b的取值范围一般为0≤b≤10，其中位置参数δ为模型随机变量X的下限，同时也为保证随机变量X不会出现负值的情况，在某一研究区域的频率分布模型中，δ表示为随机变量X在该研究区域的最小值。将指数Gamma分布采用积分法进行积分，可以得到指数Gamma分布的超越概率分布函数F(x)。在水文频率分析中，通常使用超越累计频率P代表F(x)，即：

(2)

2.1 矩法

(3)

(4)

(5)

(6)

式中：

v1——一阶原点矩；

μ2——二阶中心矩；

μ3——三阶中心矩;

μ4——四阶中心矩。

其中：

(7)

(8)

μ3=[Γ2(α)Γ(α+3b)-3Γ(α+b)Γ(α+2b)+2Γ3(α+b)]/β3bΓ3(α)

(9)

μ4=[Γ3(α)Γ(α+4b)-4Γ2(α)Γ(α+b)Γ(α+3b)+6Γ(α)Γ2(α+b)Γ(α+2b)-3Γ4(α+b)]/[β4bΓ4(α)]

(10)

2.2 优化适线法

应用矩法，可以得到指数Gamma分布设计值的计算公式[1]：

(11)

式中：

(12)

离差绝对值和最小准则为：

(13)

式中：

xi——经验频率Pi下的水文实测值；

xi*——相应频率下估计值。

以α、b、β、δ作为未知参数，选用离差绝对值和最小准则作为目标函数求解各参数值。

2.3 参数等值线图法

2.4 指数Gamma分布样本矩的计算

设样本序列长度为n，将样本序列按降序排列为xi(i= 1, 2,…,n)，频率计算公式为：

(14)

(15)

(16)

(17)

(18)

3 应用实例

查阅《广东省暴雨参数等值线图》(2003年版)，获取江谷水库、大垌、潭布、塘下的水文频率特征参数，分别以指数Gamma分布和P-Ⅲ型分布作为频率分布曲线，采用参数等值线图法进行水文频率分析。选取江谷水库、大垌、潭布、塘下4个水文测站的年最大3 d暴雨实测序列，以指数Gamma分布作为频率分布曲线，采用优化适线法进行水文频率分析。对比基于指数Gamma分布的参数等值线图法分析结果与其余两种方法的拟合情况，分析指数Gamma分布在无资料地区水文频率分析的适用性。本文所选暴雨资料通过了“三性审查”，符合水文频率计算的要求，研究区域的水文资料系列长度见表1所示。

表1 暴雨资料系列长度

3.1 参数估计及曲线拟合

表2 各站点指数Gamma分布参数估计结果

本文选取4个雨量站的年最大3 d暴雨实测序列作为研究对象，对比分析2种参数估计方法下指数Gamma分布和参数等值线图法下P-Ⅲ型分布对经验点据的拟合情况，拟合情况如图1所示。由图1可知，优化适线法、参数等值线图法和P-Ⅲ型分布确定的频率曲线均能够很好的拟合经验点距的各个部分，且表现稳定。其中，优化适线法确定的频率曲线对经验点距的上部和中部具有更好的拟合效果，2种分布曲线的参数等值线图法拟合效果次之；而对于经验点距的下部，2种分布曲线的参数等值线图法表现出更好的拟合效果。

a 江谷水库

b 大垌

c 潭布

d 塘下

3.2 误差分析

采用AIC准则和均方根误差为评价标准，进一步对比分析指数Gamma分布2种参数估计方法与P-Ⅲ型分布的拟合效果，计算结果见表3所示。

综合表3与图1的对比分析结果可以得出，4个雨量站暴雨频率分析中，指数Gamma分布2种参数估计方法计算结果的AIC指数和均方根误差普遍较小。指数Gamma分布2种参数估计方法中，部分站点优化适线法的结果明显优于参数等值线图法，这与参数等值线图精度不足，参数只能取大概数值有关。作为无资料地区的暴雨频率分析方法，参数等值线图法的结果虽然部分站点不如由暴雨实测序列计算出的结果，但其结果仍具有很大参考价值，甚至在取值准确的情况下，结果还要优于优化适线法。

表3 指数Gamma分布设计值误差比较

4 结语

本文以江谷水库、大垌、潭布和塘下4个雨量站的年最大3d暴雨资料为例，将基于指数Gamma分布的参数等值线图法应用于无资料地区的暴雨频率分析，并对优化适线法、参数等值线图法和基于P-Ⅲ型分布的参数等值线图法进行了频率曲线的拟合效果评价与误差分析，评价分析结果如下：

1) 优化适线法、参数等值线图法和基于P-Ⅲ型分布的参数等值线图法均能够很好地拟合经验点据各个部分，且指数Gamma分布2种参数估计方法计算结果的AIC指数和均方根误差普遍较小。表明在暴雨频率分析中，基于指数Gamma分布的参数等值线图法是一种可选的参数估计方法。

2) 对比优化适线法，参数等值线图法确定的频率曲线能够更好的拟合经验点距的下部，更适合做为小频率水文设计值的计算方法，能够很好的拟合经验点据的上部。

3) 文中研究了无资料地区基于参数等值线图法指数Gamma分布的频率计算。对于随机模拟法、区域化方法和径流系数法在指数Gamma分布上的应用有待进一步研究。