运输时间对水泥-石灰石粉浆体屈服应力的影响
胡晓妍, 肖 佳,*, 韩凯东, 张泽的, 田承宇
(1.中南大学 土木工程学院,湖南 长沙, 410075;2.中国电力建设集团有限公司中国水利水电第八工程局有限公司科研设计院,湖南 长沙, 410004)
石灰石粉资源丰富、分布广泛,用做水泥基材料具有良好的经济效益和环境效益[1].实际工程应用中,混凝土到达施工现场需要一定的运输时间,而运输时间不同,混凝土的流动性也有所不同[2].已有研究表明,随着运输时间的增加,混凝土的流动度和流动速率均有所减小[3].Khalid 等[4]研究发现长时间运输会引起混凝土坍损,且不同种类掺合料对混凝土坍损的影响程度不同.也有学者提出异议,如Amini等[5]研究发现连续运输会增大颗粒的堆积密实度和水膜厚度,进而增大浆体的流动度.由此可见,关于运输时间对浆体流动性、流变性能的研究主要集中于宏观性能方面且仍存在争议,其内在机理的揭示仍较为缺乏.研究表明,水泥浆体水化早期颗粒间作用力是影响其流变性能的关键因素[6],运输时间的不同会改变浆体内部颗粒的堆积状态[5],使颗粒间作用力发生变化,进而影响浆体的屈服应力.因此,研究运输时间对浆体颗粒间作用力的影响并建立浆体屈服应力与颗粒间作用力的关系,对揭示运输时间对混凝土流变性能的作用机制有重要的参考价值.
基于此,本文研究了运输时间对水泥-石灰石粉浆体屈服应力的影响,并基于EDLVO 理论计算不同运输时间下浆体的颗粒间作用力,同时采用BP 神经网络建立了浆体屈服应力与颗粒间总作用力的关系,以揭示不同运输时间对浆体屈服应力的影响机制.
1 试验
1.1 原材料
水泥(C)采用中国联合水泥集团有限公司产P∙I 42.5 基准水泥,比表面积和密度分别为347 m2/kg和3.14 g/cm3,平均粒径为17.165 μm.石灰石粉来自湖北荆门,CaCO3含量(质量分数,文中涉及的含量、水胶比等除特别说明外均为质量分数或质量比)为99%,密度为2.7 g/cm3,将其分别磨至比表面积为411、608、807、1 007 m2/kg,依次记为LⅠ、LⅡ、LⅢ、LⅣ,平均粒径分别为16.996、10.468、7.162、5.321 μm.拌和水采用自来水.水泥-石灰石粉浆体配合比见表1.

表1 水泥-石灰石粉浆体配合比Table 1 Mix proportions of cement‐ground limestone pastes
1.2 试验方法
1.2.1 流变性能测试
水泥-石灰石粉浆体采用Hobert N50 搅拌机先慢搅2 min,再快搅2 min,然后分别以4 r/min 的转速连续搅拌2、8、14 min 后静置,最后测试20 min 时浆体的屈服应力(τ).需要说明的是,根据JGJ/T 283—2012《自密实混凝土应用技术规程》,将转速设置为4 r/min 是为了模拟混凝土在运输过程中受到的搅拌作用.浆体的屈服应力(τ)通过Anton Paar公司产RHEOLAB QC 型旋转黏度计测定得到,转子为十字形,试验温度为20 ℃.为使浆体达到相同的初始状态,先以200 s-1的剪切速率对浆体预剪切30 s,再对浆体进行流变性能测试,即在60 s 内剪切速率由1 s-1对数增加到200 s-1,保持200 s-1的速率恒定剪切30 s,最后在60 s 内再次将剪切速率减小至1 s-1.采用Herschel‑Bulkley 模型拟合浆体的剪切应力-剪切速率(τ̇‑γ̇)曲线,从而得到其屈服应力.
1.2.2 堆积密实度测试
采用湿堆积法[7]测定浆体中颗粒的堆积密实度(ϕ).即在一定运输时间下,通过改变浆体的用水量得到不同水胶比的浆体;将拌和后的浆体置于已知体积的模具中,并分别计算不同水胶比下浆体的颗粒体积;由于颗粒体积最大时所对应的用水量称为标准用水量,由此得到不同运输时间下浆体的标准用水量.不同运输时间下浆体中颗粒的堆积密实度计算表达式见式(1)[8]:
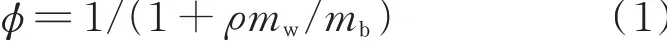
式中:ρ为水泥-石灰石粉混合料与水的相对密度;mw为水泥-石灰石粉浆体的标准用水量,g;mb为水泥和石灰石粉的总质量,g.
1.2.3 离子浓度测试
采用德国斯派克分析仪器公司产等离子光谱仪测定Na、K、Ca、S 的浓度,经计算得到Na+、K+、Ca2+、SO2-4的浓度.采用pH 计(PHS‑3E)测定离心液的pH值,精度为0.01,计算得到OH-的浓度.Debye 长度由式(2)计算[9],部分结果见表2.
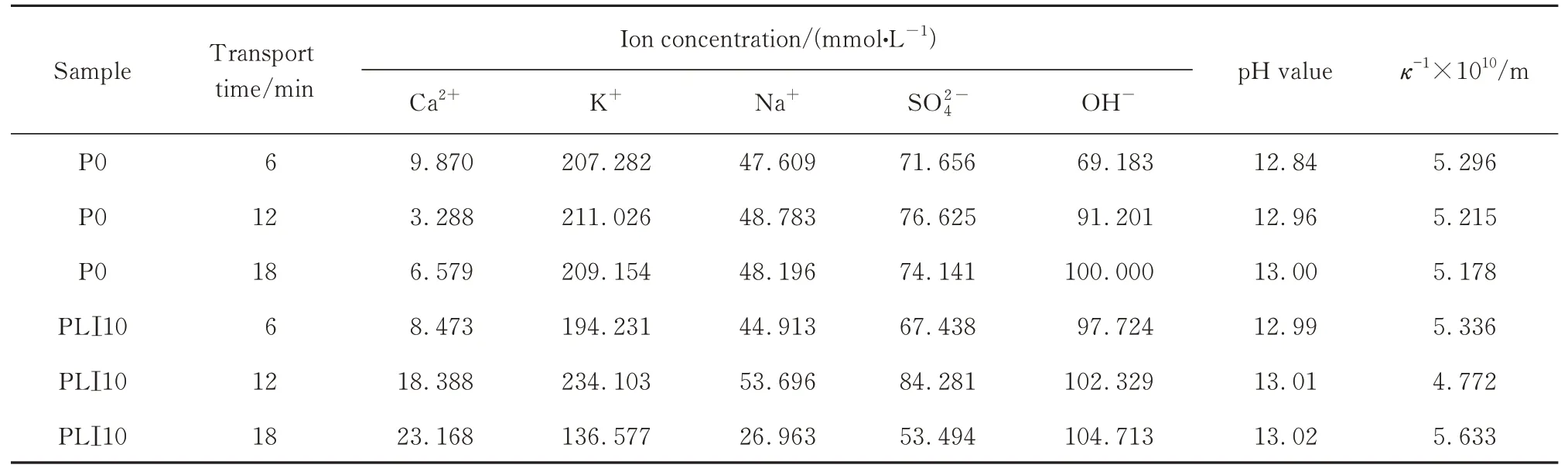
表2 水泥-石灰石粉浆体离子浓度、pH 值及Debye 长度Table 2 Ion concentration,pH value and Debye length of cement-ground limestone pastes
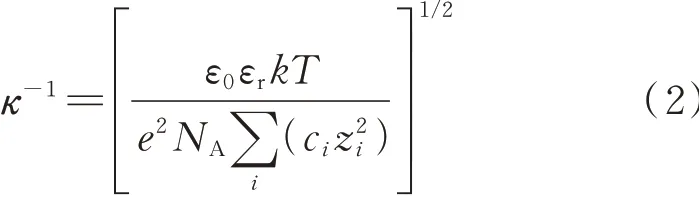
式中:κ-1为Debye 长度,m;ε0为真空的绝对介电常数,8.854×10-12F/m;εr为分散介质(水)的相对介电常数,78.5;k为Boltzmann 常数,1.38 ×10-23J/K;T为绝对温度,293 K;e为元电荷电量,1.6×10-19C;NA为阿伏伽德罗常数,6.022×1023mol-1;ci为离子浓度,mol/L;zi为离子化合价.
1.2.4 Zeta 电位测试
采用美国Colloidal Dynamics 公司产Zeta 电位仪测定水泥和石灰石粉颗粒表面Zeta 电位.在320 g水中加入60 g 水泥或石灰石粉,先慢搅2 min,再快搅2 min,将悬浮液倒入电位测定仪,测试20 min 时的Zeta 电位[10],测试结果见表3.
1.2.5 粉体表面能测试
采用上海中晨数字技术设备有限公司产接触角测试仪测试水泥和石灰石粉试样表面的接触角(θ),测试液为去离子水、甲酰胺和乙二醇.试样制备方法:先将粉体材料与无水乙醇以质量比1∶1 混合并快搅3 min,取2.5 mL 悬浮液置于26 mm×76 mm 的载玻片上,随后将载玻片放入40 ℃的烘箱中烘干6 h,以除去材料表面的无水乙醇.粉体表面能计算式见式(3)[11],计算结果也列于表3.
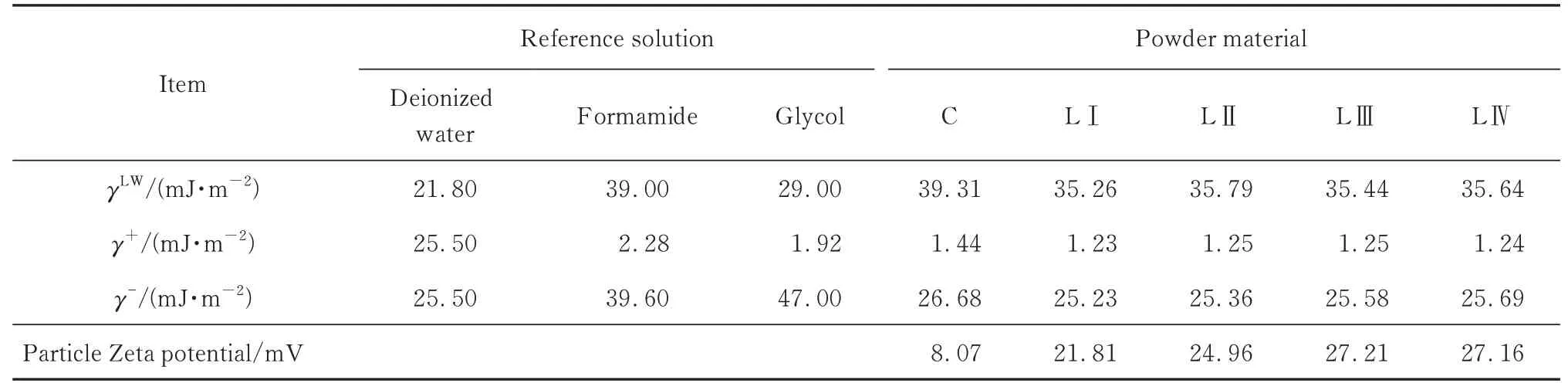
表3 水泥和石灰石粉颗粒的表面能与Zeta 电位Table 3 Surface energy and Zeta potential of cement and ground limestone particles
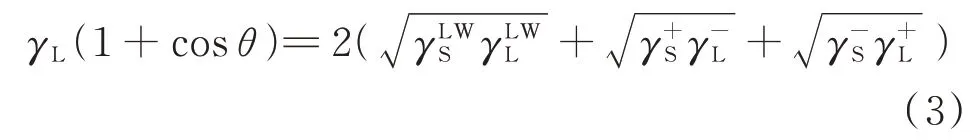
式中:γL为液体的界面张力,mJ/m2;γLWS、γLWL分别为粉体颗粒和液体界面张力的Lifshitz van der Waal 分量,mJ/m2;γ+S、γ+L分别为粉体颗粒和液体界面张力的Lewis 酸分量,mJ/m2;γ-S、γ-L分别为粉体颗粒和液体界面张力的Lewis碱分量,mJ/m2.
2 结果与讨论
2.1 水泥-石灰石粉浆体的屈服应力
图1为不同运输时间下水泥-石灰石粉浆体的屈服应力(τ)随颗粒总比表面积(Scl)的变化.Scl计算式[12]为Scl=Scφc+Slφl,其中,Sc、Sl分别为水泥、石灰石粉颗粒的比表面积,μm2/μm3;φc、φl分别为水泥、石灰石粉颗粒占固体颗粒的体积分数.由图1 可知:各运输时间下,随着颗粒总比表面积的增加,水泥-石灰石粉浆体的屈服应力均先减后增,当颗粒总比表面积为1.113 μm2/μm3时,浆体的屈服应力值最小;随着运输时间的增加,浆体的屈服应力逐渐增大.
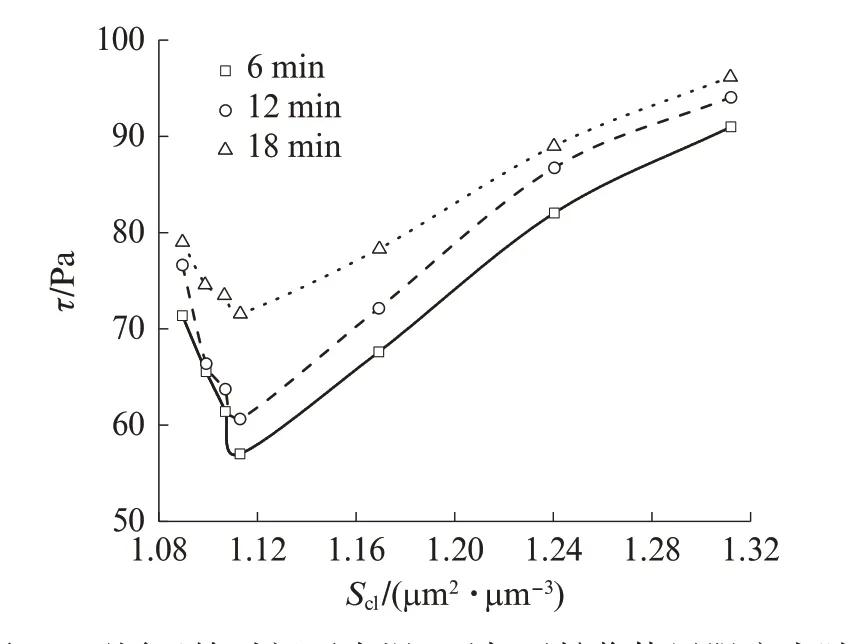
图1 不同运输时间下水泥-石灰石粉浆体屈服应力随颗粒总比表面积的变化Fig.1 Variation of yield stress of cement‑ground limestone paste with total specific surface area under different transport time
外界扰动会改变浆体中颗粒的堆积状态,不同运输时间下颗粒堆积状态发生了明显变化[5].
图2为不同运输时间下水泥-石灰石粉浆体颗粒堆积密实度(ϕ)和水膜厚度(dw)的变化.由图2(a)可见:各运输时间下浆体颗粒的堆积密实度随着颗粒总比表面积的增大先增后减,当颗粒总比表面积大于1.169 μm2/μm3时,颗粒的堆积密实度几乎没有变化;随着运输时间的增加,颗粒的堆积密实度逐渐减小.颗粒的堆积密实度越大表明其堆积状态越好,颗粒间空隙越小,在用水量不变的条件下体系多余水量越多,浆体的流动性就越好.由此说明,随着运输时间的增加,浆体的流动性变差.
研究发现,相比于颗粒的堆积密实度和总比表面积等颗粒群特性对浆体屈服应力的影响,颗粒的水膜厚度是影响浆体屈服应力更重要的参数,其计算式见式(4)[13]:
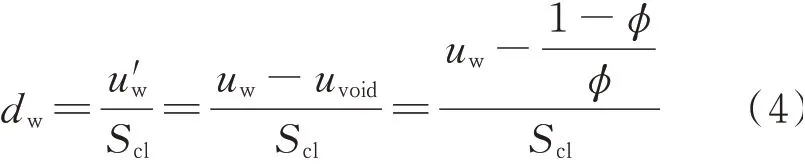
式中:u′w为多余水与固体的体积比(多余水比);uw为总用水与固体的体积比;uvoid为空隙与固体的体积比.
由图2(b)可见:整体上,随着颗粒总比表面积的增加,其水膜厚度先增大后减小;随着运输时间的增加,颗粒水膜厚度逐渐减小.颗粒水膜厚度取决于颗粒的堆积密实度和总比表面积之比,并随比值的增大而增大[14].当颗粒的总比表面积为1.099、1.113 μm2/μm3时,颗粒水膜厚度较大,这是因为其对应的堆积密实度和总比表面积比值较大.当运输时间为6 min 时,水泥-石灰石粉浆体颗粒堆积密实度与总比表面积之比如表4 所示.
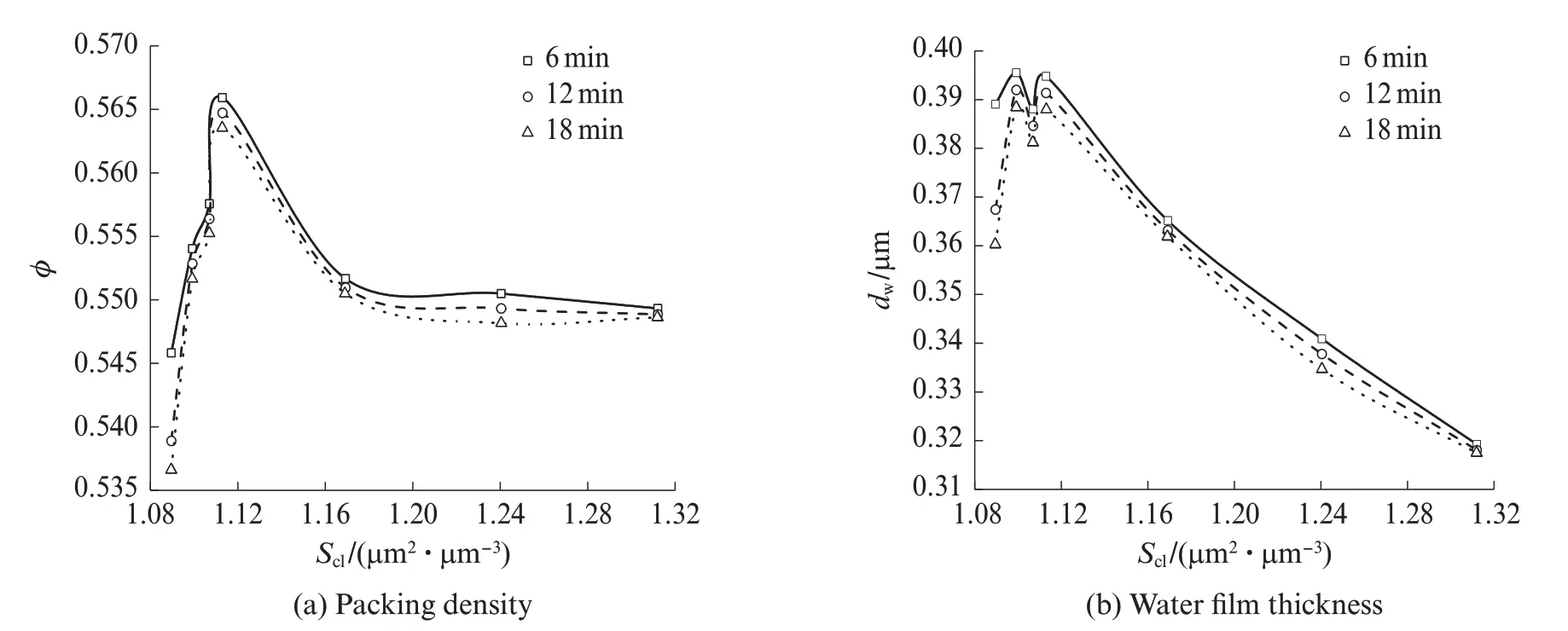
图2 不同运输时间下水泥-石灰石粉浆体的颗粒堆积密实度和水膜厚度Fig.2 Packing density and water film thickness of cement‑ground limestone paste under different transport time

表4 运输时间为6 min 时水泥-石灰石粉浆体颗粒堆积密实度与总比表面积之比Table 4 Ratio of packing density and total specific surface area of cement-ground limestone paste at transport time of 6 min
颗粒水膜厚度可间接表示颗粒之间的距离,水膜厚度越小,颗粒间距越小,颗粒间作用力就越大;同时,包裹在颗粒表面的水膜层具有润滑、减小颗粒间摩擦力的作用.图3 为水泥-石灰石粉浆体颗粒水膜厚度与屈服应力的关系.由图3可见,颗粒水膜厚度与浆体屈服应力具有良好的负相关性,随着颗粒水膜厚度的增大,浆体屈服应力减小.颗粒水膜厚度的变化定性说明了不同运输时间下浆体屈服应力的变化.
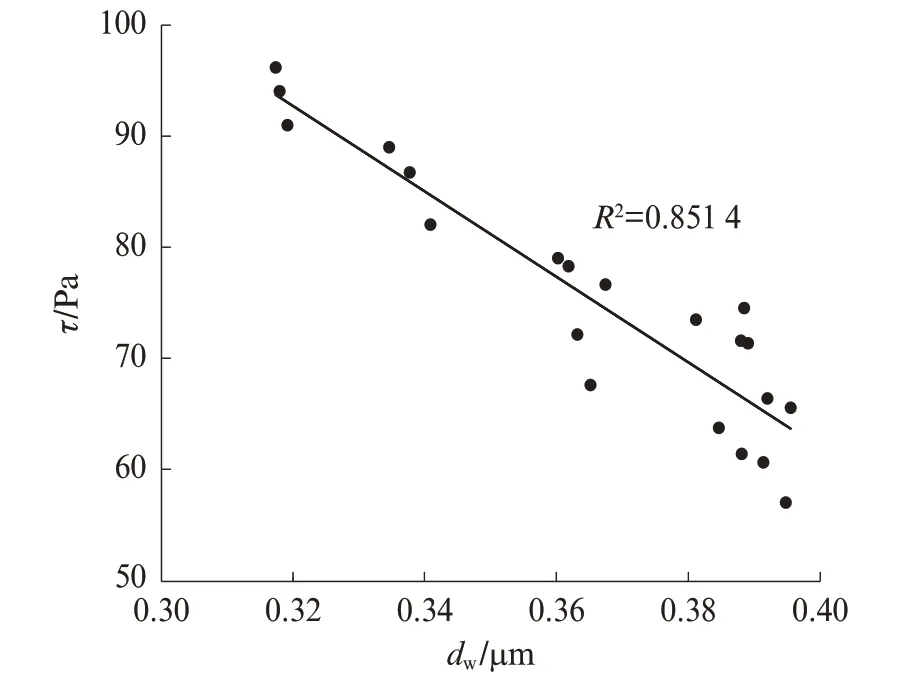
图3 水泥-石灰石粉浆体颗粒水膜厚度与屈服应力的关系Fig.3 Relationship between water film thickness and yield stress of cement‑ground limestone paste
颗粒水膜厚度的变化实际上反映了颗粒间距的改变,本质是改变了颗粒间的作用力.为研究运输时间对水泥-石灰石粉浆体屈服应力的影响机制,本文基于EDLVO 理论计算了不同水泥-石灰石粉浆体的颗粒间作用力.
2.2 不同运输时间下水泥-石灰石粉浆体颗粒间作用力的变化
EDLVO 理论通过颗粒表面物理化学作用解释颗粒间发生凝聚的机制,该理论已被广泛地应用于水泥基材料颗粒间作用力的研究[15‑16]中.基于EDLVO理论,水泥-石灰石粉浆体颗粒间总作用力(FT)包括范德华力(FLW)、水合作用力(也称A‑B 作用力(FAB))和静电力(FEL)[17].各作用力计算式见式(5):
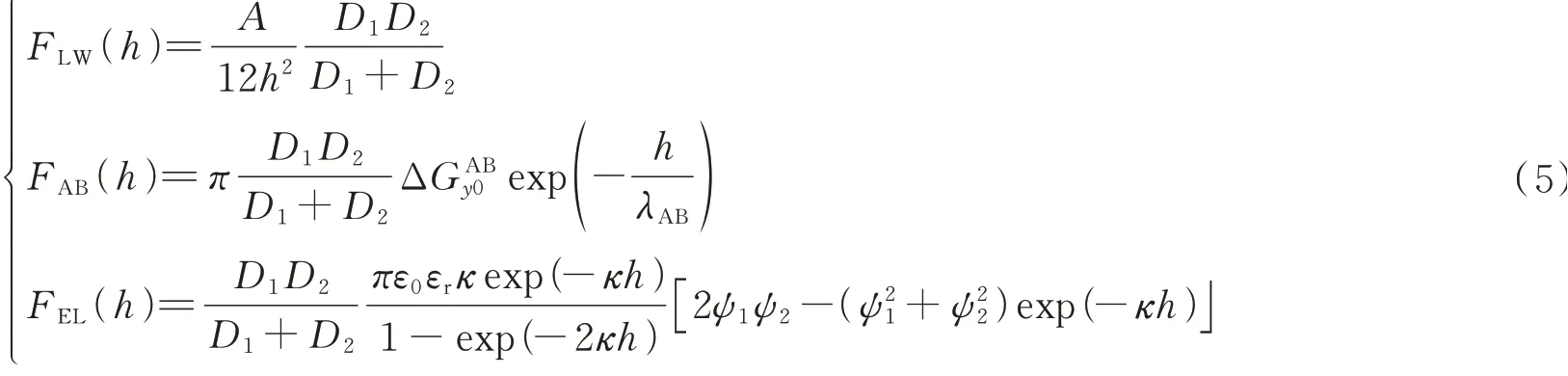
式 中:A为Hamaker 常数其中h0是由波恩排斥力导致的颗粒之间最小距离,0.158 nm分别为水泥和石灰石粉颗粒界面张力的Lifshitz van der Waal分量,mJ/m2;h为颗粒表面间距,m;D1、D2分别为两相邻颗粒的平均直径,D1D2/(D1+D2)为颗粒等效粒径,m;λAB为衰减长度为介质中2 个颗粒交界面上单位面积的酸碱自由能[17],mJ/m2;ψ1、ψ2分别为2 个胶体颗粒的表面电势,近似等价为颗粒Zeta 电位,mV.
图4为不同运输时间下水泥-石灰石粉浆体颗粒间作用力随颗粒表面间距的变化.由图4(a)、(b)可见:随着颗粒表面间距的增大,范德华力以二次方的速率减小,A‑B 作用力呈指数型递减;同一颗粒间距下,随着石灰石粉掺量和细度的增加,范德华力和A‑B 作用力均逐渐减小.由式(5)可知,同一颗粒间距下,颗粒等效粒径、表面能是影响范德华力和A‑B 作用力的主要因素,由于水泥颗粒和石灰石粉颗粒的表面能差别不大,因此范德华力和A‑B 作用力的不同主要受颗粒等效粒径的影响.本文采用的石灰石粉粒径小于水泥颗粒,且石灰石粉细度越大其粒径越小,因此随着石灰石粉掺量和细度的增加,颗粒等效粒径减小,进而降低了范德华力和A‑B 作用力.运输时间主要通过影响颗粒间距改变范德华力和A‑B 作用力,因此将在下文讨论其对颗粒间作用力的影响.由图4(c)可见:(1)随着颗粒间距的增大,浆体的静电力以指数型速率减小;同一间距下,静电力主要受颗粒等效粒径、Debye长度等因素的影响,石灰石粉的掺入减小了颗粒等效粒径,对静电力有减小作用,而Debye 长度和Zeta 电位随石灰石粉掺量、细度的改变,并没有明显的变化规律且其对静电力的影响较为复杂.运输时间通过改变Debye 长度(表2)、颗粒间距来影响静电力.(2)不同运输时间下,浆体的静电力随石灰石粉掺量、细度的变化并不相同,但石灰石粉掺量为20%、30%时静电力较大.结合表2 的Debye 长度研究发现,本试验中Debye 长度对静电力的影响占主导作用,如各运输时间下石灰石粉掺量由0%增加至10%时,浆体的静电力变化规律与Debye 长度的变化规律一致.
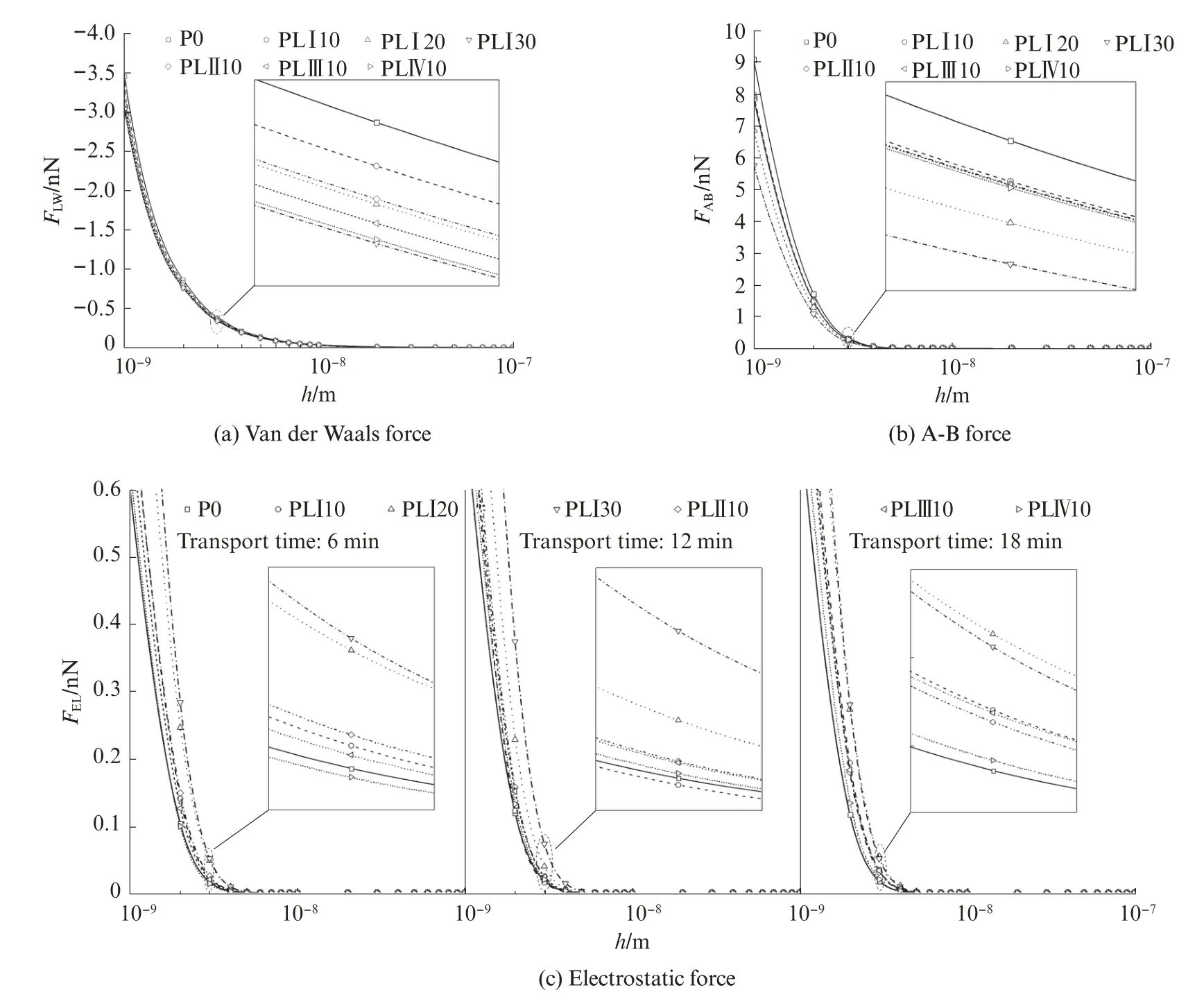
图4 不同运输时间下水泥-石灰石粉浆体颗粒间作用力随颗粒表面间距的变化Fig.4 Variations of interparticle forces of cement‑ground limestone paste with separation distance under different transport time
图5为不同运输时间下水泥-石灰石粉浆体颗粒间总作用力(FT)随颗粒表面间距的变化.由图5 可以看出:(1)随着颗粒间距的增大,FT先表现为排斥力,后转变为吸引力,运输时间未改变FT随颗粒表面间距的变化规律.(2)同一颗粒间距下,不同体系的FT相差不大,这主要是范德华力、A‑B 作用力和静电力等3 种作用力共同作用的结果.如当颗粒表面间距为3 nm,运输时间为6 min时,石灰石粉掺量10%浆体的范德华力和A‑B作用力分别为-0.366 3、0.284 2 nN,大于石灰石粉掺量20%浆体的-0.351 6、0.244 5 nN;而石灰石粉掺量10%浆体的静电力为0.022 0 nN,小于石灰石粉掺量20%浆体的0.047 6 nN,2 个体系的总作用力之差仅为0.000 6 nN,远小于范德华力的数量级,说明同一颗粒间距条件下2 个体系总作用力的差别微小.
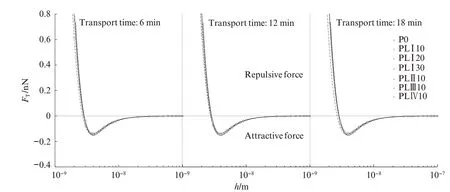
图5 不同运输时间下水泥-石灰石粉浆体颗粒间总作用力随颗粒表面间距的变化Fig.5 Variations of FT of cement‑ground limestone pastes with separation distance under different transport time
然而,值得注意的是,图4、5 主要讨论了同一颗粒间距下不同体系颗粒间作用力的变化,而实际上不同体系的颗粒间距不同,因此颗粒间作用力的计算必须要考虑颗粒间距的作用(式(4)).前文研究发现,运输时间对颗粒水膜厚度有明显的影响.假定粉体颗粒的大小相同,理想条件下可将颗粒水膜厚度的2 倍视为平均颗粒间距,则运输时间将会改变浆体内颗粒的平均间距,从而改变颗粒间作用力,最终影响浆体的屈服应力.因此,研究不同运输时间下浆体屈服应力的影响机制必须考虑运输时间对颗粒表面间距的作用.
2.3 不同运输时间下颗粒间作用力与屈服应力的关系
表5为不同运输时间下水泥-石灰石粉浆体平均颗粒间距的计算结果.由表5 可知,平均颗粒间距随运输时间的变化规律与水膜厚度相同,即随着运输时间的增加,平均颗粒间距减小.水化初期,屈服应力主要取决于颗粒间作用力,随颗粒间作用力的增大而增大,随表面间距的增大而减小[18‑19].基于此,建立了水泥-石灰石粉浆体屈服应力与颗粒间总作用力的关系式其中FT取最大颗粒间作用力.
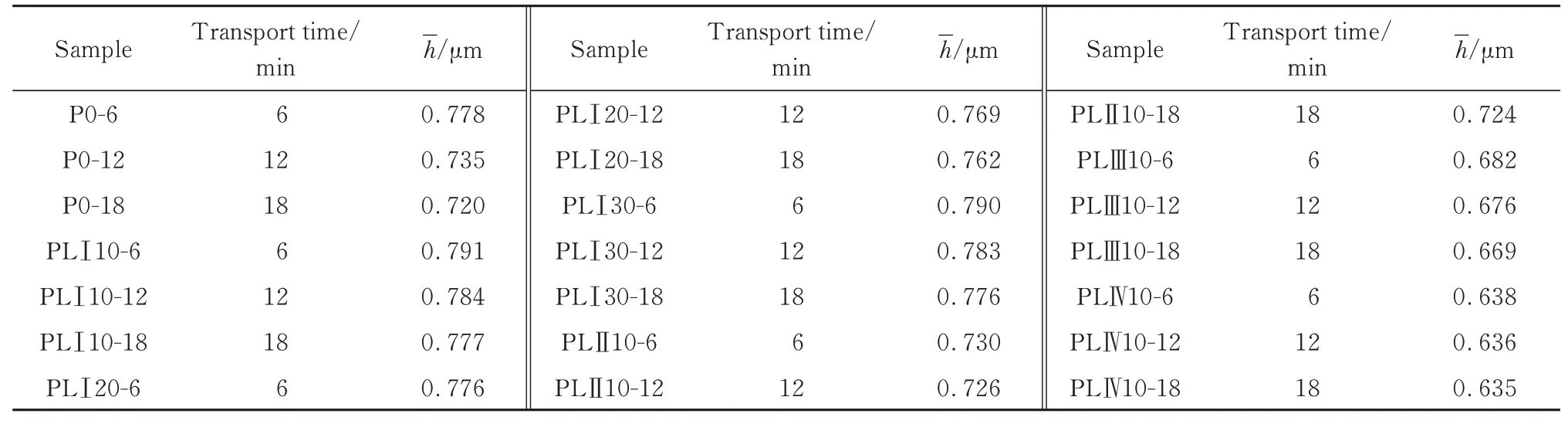
表5 不同运输时间下水泥-石灰石粉浆体平均颗粒间距Table 5 Average particle spacing of cement‐ground limestone pastes under different transport time
为探究水泥-石灰石粉浆体τ与之间的关系,测定了各运输时间下水胶比为0.38、0.42 的水泥-石灰石粉浆体的屈服应力.采用BP 神经网络对水胶比为0.40 的水泥-石灰石粉浆体的τ和进行训练,其中τ为输入为输出,预测水胶比为0.38、0.42 时 浆 体 屈 服 应 力 对 应 的,以 建 立 水泥-石灰石粉浆体与τ的关系.本文BP 神经网络模型输入、输出层神经元个数均为1,隐含层神经元个数为5.输出层和隐含层神经元激励函数分别为logsig 和tansig,训练函数为traingdx,性能函数为mse,迭代参数为5 000,期望误差为0.000 000 1[20].表6 展示了部分神经网络预测结果.
由表6 可知,回归系数R2均大于0.95,表明预测结果准确度较高,十分接近实际值.基于浆体τ与FT/试验值和BP 神经网络预测值,可得到水泥-石灰石粉浆体τ与的关系,如图6 所示.由图6 可知:浆 体τ与之 间 的 关 系 可 用b)+c表示,其中a、b、c为经验参数;随着的增大,τ呈对数增加.该式建立了水泥-石灰石粉浆体屈服应力与颗粒间作用力的半定量关系,揭示了不同运输时间下水泥-石灰石粉浆体屈服应力的影响机制.

表6 BP 神经网络预测结果Table 6 Prediction results of BP neural Network
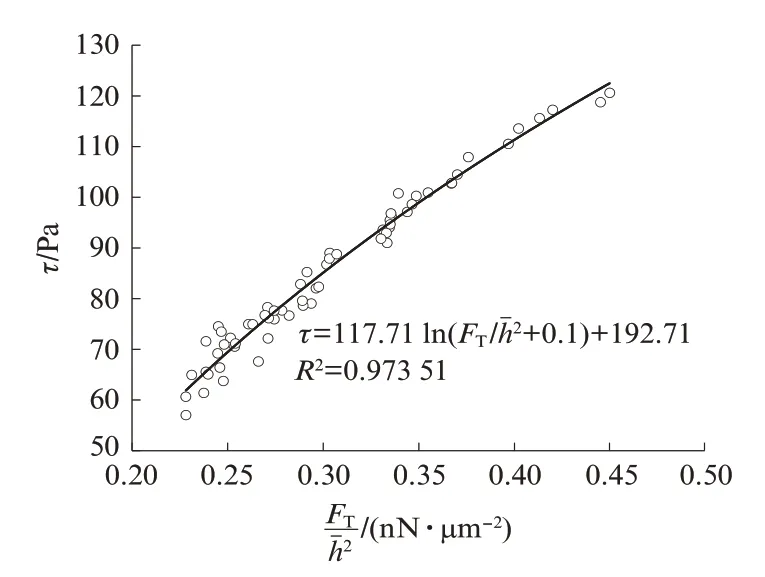
图6 水泥-石灰石粉浆体τ 与 的关系Fig.6 Relationship between τ and of cement‐ground limestone paste
3 结论
(1)各运输时间下水泥-石灰石粉浆体的屈服应力随着颗粒总比表面积的增加先减后增;随着运输时间的增加,浆体的屈服应力逐渐增大.颗粒水膜厚度可表征不同运输时间下浆体屈服应力的变化,与屈服应力具有良好的负相关性.
(2)同一颗粒间距下,随着石灰石粉掺量和细度的增加,水泥-石灰石粉浆体的范德华力和A‑B作用力逐渐减小,静电力没有明显变化规律;Debye 长度对静电力的影响占主导作用,静电力变化规律同Debye 长度的变化规律一致;同一颗粒间距下,不同水泥-石灰石粉浆体颗粒间的总作用力变化较小.
(3)随着运输时间的增加,水泥-石灰石粉浆体的平均颗粒间距减小.建立了不同运输时间下浆体屈服应力与颗粒间总作用力的关系.

