中国城镇化水平增长曲线分段拟合与预测*

□刘书成 程开明 吴浈凯 柴燚

城镇化是当今世界最重要的社会经济现象之一，是推动经济发展和国家现代化的重要动力，也是社会进步的必然趋势。然而，城镇化水平与经济发展的不匹配性也带来一系列问题，诸如土地过度开发、城乡差距扩大等。中国大力推进以人为核心的新型城镇化发展战略，目的是实现城镇化进程由“量”的增加到“质”的提升转变。

2020年中国城镇化水平达63.89%，已迈入城镇化快速发展中后期，呈现出“多期”叠加的新特征。未来一段时期，中国城镇化发展态势如何？这一问题涉及到采用什么样的推进与调控策略，以进一步释放城镇化对经济社会发展的带动效应。因此，运用科学方法对中国城镇化水平做出合理预测，能够明晰中国城镇化发展态势，为后续战略措施和政策制定提供依据，促进城镇化与经济协调高质量发展。

目前，国内外学者针对城镇化水平增长曲线的拟合方法较多，其中常用的方法主要包括Logistic 增长模型、时间序列分析模型、城镇化水平与经济变量的回归模型，也有部分学者采用灰色预测模型、神经网络模型等（兰海强等，2014）。然而，这些方法在实际应用中均存在一定的不足之处，譬如中国城镇化水平并不满足“S”型曲线特征、时间序列模型的选择存在主观性和不易解释性、回归模型容易遗漏变量、灰色预测模型的短期性以及神经网络模型的“黑箱”性质等。为弥补这些不足，本文尝试引入一种新方法——自动分段曲线拟合，为预测城镇化水平提供新思路，并开展改革开放以来中国城镇化水平的实际拟合及效果检验，对2021-2025年的城镇化水平做出预测。

｜现有的城镇化水平拟合方法

（一）Logistic 增长模型

诺瑟姆（Northam,1975）将不同国家和地区人口城市化进程的共同规律概括为一条被拉平的S 型曲线，并把城市化进程分为初期、中期和成熟期三个阶段。Karmeshu(1992) 通过梳理20 世纪50年代以来发达国家的城市化发展进程也发现，随着经济不断发展，城市化水平的增长曲线大致表现为一条拉伸的“S”型曲线，这一曲线特征可用Logistic 增长模型进行拟合。通常，有两种方式推导出城镇化水平增长的“S”型曲线：一是城乡人口增长率差值法；二是城镇化率变化时间路径法。

1.城乡人口增长率差值法。设U0、R0分别为基期(t=0) 城镇人口和农村人口，u、r 分别为t 期城市人口和农村人口的指数增长率，那么t 期城市人口Ut 和农村人口Rt可表示为：

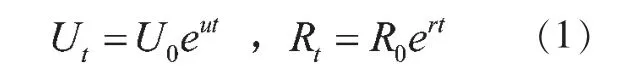
由式（1）可推算出t 期的城镇化率yt为：

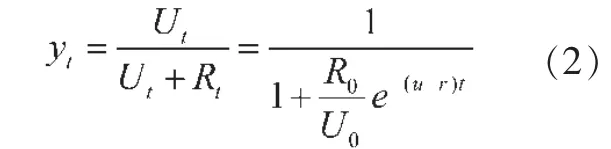
2.城市化率变化时间路径法。已知t 期城镇人口增长率ut和农村人口增长率rt分别为：

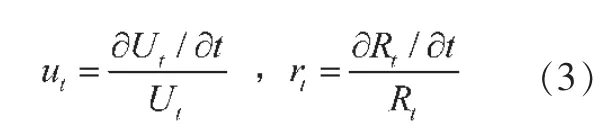
那么，城乡人口增长率之差dt为：dt=ut-rt，城镇化率速度为：

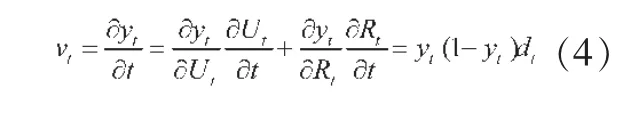
若dt=b 是常数，由式（2）和式（4）可得：

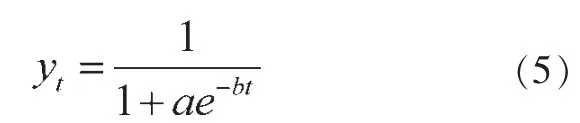
其中，yt表示城镇化率；a 为积分常数，反映城镇化开始时间的早晚；b 为斜率，反映城镇化发展速度的快慢。一般而言，将式（5）称作城镇化水平的“S”(Logistic) 型增长曲线，城镇化率饱和值为100%。

王远飞和张超（1997）探讨了以Logistic 模型拟合城镇化水平的合理性，指出城镇化率的饱和值可以不为100% (80%以上)。宋丽敏（2007）采用Logistic 增长模型预测2030年中国城镇化率将达到60%，实践证明这一结果明显偏低。简新华和黄锟（2010）对Logistic 模型作对数变换后拟合中国城镇化率，结果显示模型拟合误差呈逐步扩大的趋势，存在显著系统性差异。曹飞（2012）基于突变结构理论对中国城镇化水平进行Logistic 模拟，指出1995年为结构突变点，表明城镇化发展受到某些外部因素的影响。

结合以上学者的研究可以发现，虽然Logistic 增长模型在城镇化水平增长曲线拟合方面具有一定适用性，但这一模型不太适用于中国，原因在于：“S”型增长曲线是基于美国等发达国家城镇化进程而得到的，中国城镇化水平显然并不满足“S”型曲线的典型特征，实际应用中需对模型结构做出调整。将Logistic 增长模型运用于中国城镇化进程拟合及预测时，需要格外关注三个方面的问题：（1）中国城乡人口增长率之差不为常数。经典“S”型增长曲线假设城乡人口增长率之差保持不变，但人口普查数据显示中国城乡人口增长率处于不断波动之中。（2）城镇化率的饱和值难以确定。经典“S”型增长曲线假设城镇化率饱和值为100%，但结合世界城镇化进程和中国经济社会发展情况，饱和值取100%显然是不切实际的。此外，这一饱和值是基于城乡人口增长率之差为常数这一条件推出的，若城乡人口增长率之差不为常数，则城镇化率饱和值不可能为100%。（3）中国城镇化发展进程并不符合Logistic 增长模型特征。自1949年新中国成立以来，城镇化水平增长曲线呈现“快—慢—快”的特征，这与Logistic 增长模型“慢—快—慢”的曲线特征有较大差异。

（二）时间序列分析模型

城镇化作为一种重要的社会经济现象，其发展是一个动态过程，兼具一定的运行规律。作为一种动态拟合方法，时间序列分析模型以年份为自变量，以城镇化水平为因变量，根据城镇化水平的变动特征构建合适的时间序列模型，以对城镇化水平进行拟合与预测。

时间序列模型的种类繁多，需要学者根据时间趋势图、自相关和偏自相关系数等信息来选取适合的模型。常见的时间序列模型有AR(p)、MR (q) 和ARMA (p,q) 等，模型具体结构分别为：

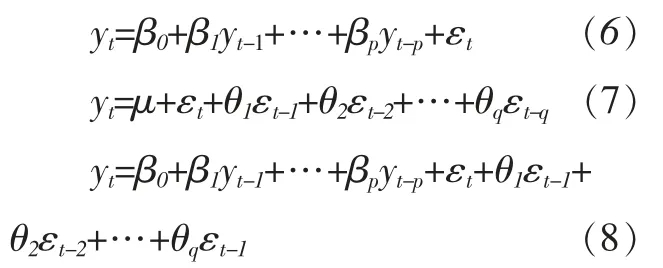
其中，yt为城镇化率，{εt} 为白噪声。

李林杰和金剑（2005）对1949-2004年城镇化水平数据作一阶差分后建立AR（1）和ARMA（1,2）模型拟合，比较发现AR（1）模型的拟合精度较高，预测2010年城镇化率为44.67%，事实证明这一预测值是偏低的。张松林和熊红轶（2009）对1949-2007年中国城镇化率进行时间序列分析，认为城镇化水平提高主要受滞后一期和滞后五期的随机误差影响，预测2010年城镇化率为46.59%。丁刚（2010）采用PDL 和ARMA 模型的组合方法，构建基于时间序列分析的混合有限PDL 模型，预测2010年中国城镇化率为51.41%，这一预测结果偏高。

时间序列分析作为一种动态分析方法，能够对城镇化水平进行拟合与预测，通常模型预测精度也较高。然而，时间序列分析存在两大缺陷：一是模型结构较为复杂，学者通常需要根据自身经验和主观判断选取所要构建的模型；二是时间序列模型只能反映城镇化水平的发展进程，而无法解释背后原因，故只适用于预测而不能开展经济解释。

（三）城镇化水平与经济变量的回归模型

城镇化与经济发展是密切相关的，这一方法通过选取与城镇化水平具有一定相关性的经济指标，以其作为解释变量来构建城镇化水平的回归模型，如简单线性回归模型、对数线性回归模型、非线性回归模型等。该方法的核心思想是根据相关经济变量的变动情况来预测未来的城镇化水平。以多元线性回归和对数线性回归为例，具体模型为：

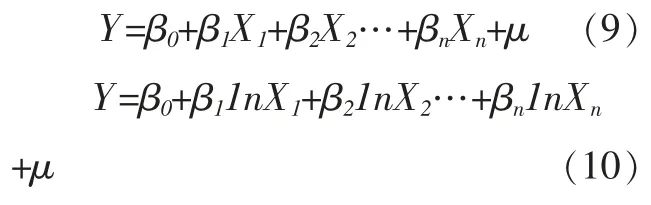
其中，Y 为城镇化率指标，Xi(i=1,…,n) 为与城镇化水平相关的经济指标，μ 为随机扰动项，式 (9)为简单线性回归模型，式(10) 为对数线性回归模型。

周一星（1995）建立城镇化指数与经济发展指数之间的对数回归模型，对城镇化水平进行拟合；基于城镇化水平与工业化、经济发展之间的相关关系，可以构建城市化率与工业劳动人口比重的一元回归模型来拟合城镇化水平。李迅等（2000）构建城镇化率与人均GDP的对数线性回归模型，预测中国2020年城镇率约为52%，这一预测结果明显偏低。王金营（2003）分别建立城镇化率与人均GDP 的线性回归模型和Logistic 曲线模型，经检验发现线性回归模型的拟合精度较高。

城镇化水平与经济变量的回归模型受到学者广泛青睐的主要原因是模型构建简单，同时易于对结果做出经济解释，这是回归模型的优势所在。然而，此类模型存在两大问题：一是虚假回归问题，虽然城镇化与众多经济指标之间存在一定的相关关系，但从长期看却不一定是均衡关系，而基于非协整的变量关系构建回归模型时可能造成虚假回归；二是解释变量的选择问题，城镇化是一个错综复杂的社会经济现象，难以将众多影响因素考虑周全，因此构建回归模型时面临着变量取舍的问题。

（四）其他模型

除以上三种拟合方法与模型外，部分学者还尝试使用灰色预测模型和BP 神经网络模型等来对中国城镇化发展水平进行拟合。白先春和李炳俊（2006）针对1992-2003年城镇化率数据，构建新陈代谢GM(1,1) 模型，发现模型拟合误差与时间间隔存在显著正相关。郭志仪和丁刚（2006）以人均GDP 为特征向量，城镇化率为响应变量，建立BP神经网络模型拟合城镇化水平与经济发展水平之间的复杂关系，拟合精度显著优于普通线性模型。

无论是灰色预测模型还是BP神经网络模型，都还存在一些弊端。灰色预测模型要求数据期数较短，长序列的拟合误差通常大于短序列，故不适用于城镇化水平这类长期增长曲线的拟合；BP 神经网络模型虽然拟合精度较高，但由于其“黑箱”性质和惯性特征，难以对结果做出经济解释，且误差率可能随预测期数延长而激增。

综上所述，现有的城镇化水平拟合模型均存在一定缺陷与不足。中国城镇化水平不满足“S”型曲线特征，故Logistic 增长模型并不适用；时间序列模型在模型形式选择上存在主观性，且只适合于预测而不适用于经济解释；回归模型难以将所有影响因素考虑周全，且容易造成虚假回归；灰色预测模型不适用于长期数据，神经网络模型具有“黑箱”性质。因此，有必要尝试引入一种新方法——自动分段曲线拟合，开展中国城镇化水平拟合及预测。

｜自动分段曲线拟合方法

多项式曲线拟合是一种常用的数据拟合方法，当数据点较多时，只采用一种多项式曲线函数进行拟合往往难以取得较好的拟合精度和效果。因此，一种改进思路是先对数据进行分段，分别采用不同的函数形式加以拟合，即分段曲线拟合方法。然而，传统分段曲线拟合主要依据主观经验和数据散点图来确定分段区间和经验函数，遇到复杂数据时可能出现较大偏差（蔡山等，2007）。为解决这一问题，本文拟采用自动分段曲线拟合，该方法具有两大优点：一是根据不同函数形式的拟合误差，自动确定拟合精度较高的经验函数形式；二是自动确定分段区间，并在每个区间内进行最小二乘拟合。

（一）最优经验函数的选取

数据拟合方法较多，具体包括简单线性拟合、对数线性拟合、二次曲线拟合、指数拟合、幂函数拟合等。一般来说，通过观察数据分布散点图可确定大致的拟合函数，但这一方式较为主观。自动分段曲线拟合的优势在于能够客观地选取最优经验函数，主要基于两个条件：（1）历史数据点误差符号相反的个数之差小于调节参数；（2）分别计算不同拟合函数误差的方差，取方差最小者为最优经验函数。误差方差的数学表达式为：

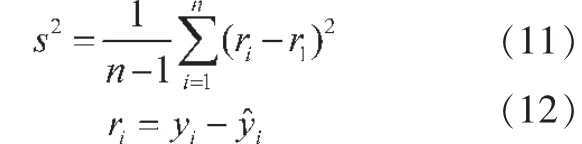
其中，r1为第一数据点的拟合误差，ri为后续数据点的拟合误差，可理解为相较于第一数据点来说，各数据点误差的波动大小。s2越小，表示各数据点的误差越接近，拟合精度越高。通过观察时间趋势图，发现中国城镇化水平存在明显的长期趋势且波动幅度较小，结合曲线特征，采用直线函数、对数函数、指数函数和多项式函数四种典型的回归方程分别进行拟合，选取最优经验函数的流程图如图1 所示。

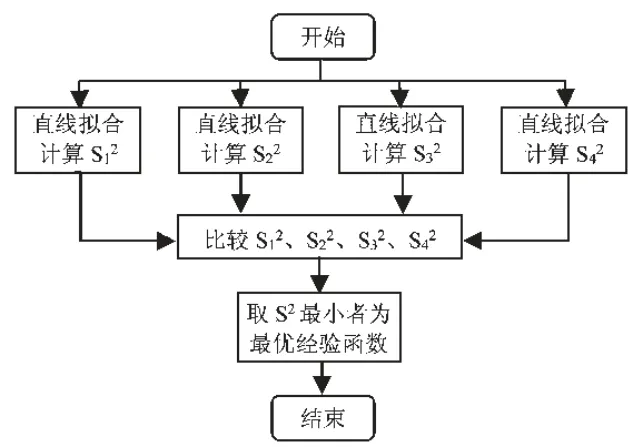
图1 选取最优经验函数的流程

图1 中，直线拟合方程为y=ax+b；对数拟合方程为y=logax；指数拟合方程为y=beax；多项式拟合方程为pn。

（二）自动分段曲线拟合的步骤

在确定最优经验函数后，可以得到各数据点的拟合误差，由此计算出误差绝对值的均值，记为S，计算公式为：

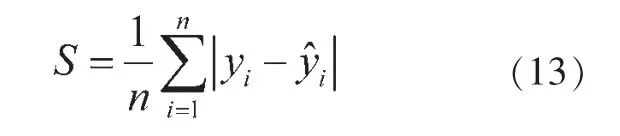
为防止分段区间过多导致过拟合，结合模型拟合效果，在此将调节参数设置为4，即若出现连续四个数据点的误差绝对值大于S，那么就从第一个数据点处分段，并对分段点后的数据重新选取最优经验函数进行拟合。依此类推，直至不会出现连续四个数据点的误差绝对值大于S 的情况。

｜中国城镇化水平增长曲线的分段拟合

新中国成立以来，受到国际局势和国内政策的影响，城镇化道路可谓是一波三折，城镇化率也呈现出较大波动。改革开放后，中国城镇化才步入一个平稳发展期。本文选取1978-2020年中国城镇化率数据，构建自动分段曲线拟合模型，拟合结果见表1 所示。

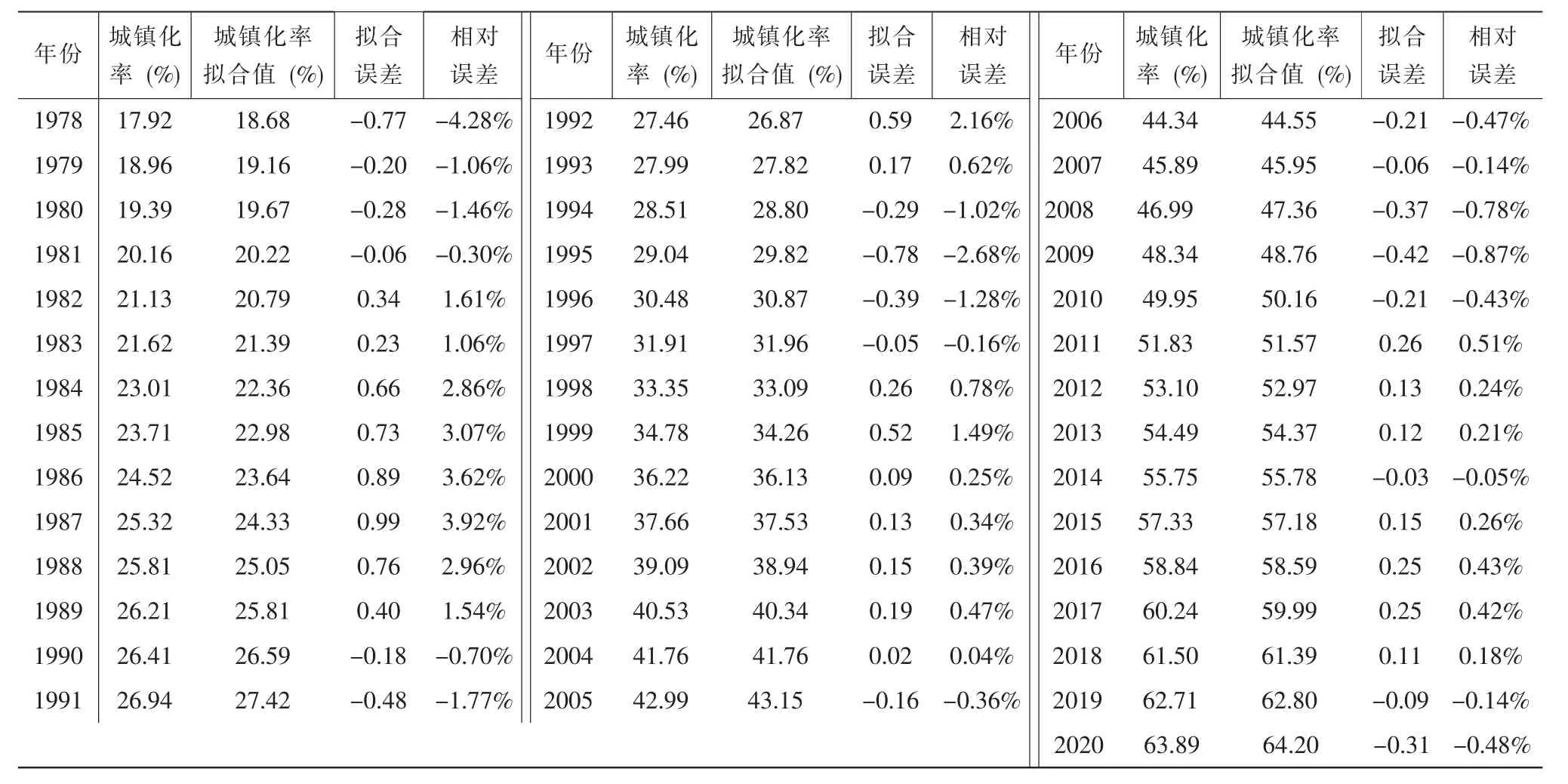
表1 中国城镇化率与拟合值比较

对于1978-2020年中国城镇化水平的拟合，模型自动将其分为四段：1978-1983年、1984-1991年、1992-1999年和2000-2020年，分别选取二次多项式函数、二次多项式函数、指数函数、直线函数作为最优经验函数进行拟合。设1978年t=1（t 为正整数），四个分段区间的模型表达式分别为：

结合城镇化发展历程，这四个分段区间分别与国家重大战略决策相对应：1984年中央实行经济体制改革，明确提出加快以城市为重点的改革步伐；1992年邓小平南方谈话重申深化改革的必要性，进一步明确扩大开放，刺激了大规模的人口流动；2000年，中央发布《关于促进小城镇健康发展的若干意见》，指出加快城镇化进程的时机和条件已经成熟。可见，模型分段点符合实际背景，具有现实意义。

由表1 可知，模型拟合精度较高，相对误差控制在5%以内，且拟合误差随时期变动呈下降趋势。结合拟合效果图可知，各个分段区间内城镇化水平变动趋势符合相应的最优经验函数特征，模型拟合存在合理性。同时，拟合曲线与实际曲线间距离不断缩小，21 世纪以来中国城镇化进入稳定的高速增长阶段，2000-2020年这一区间内的平均拟合误差也达到最小。进一步利用自动分段曲线模型对未来中国城镇化率进行预测，为保证预测精度，仅将预测期延长至2025年，结果见表2。2021-2025年中国城镇化水平平均每年提升1.47 个百分点，2025年城镇化水平预计达71.22%。

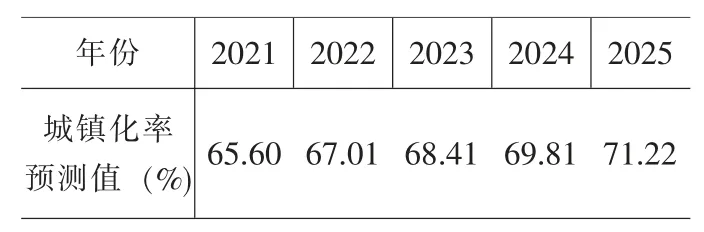
表2 中国城镇化率预测结果

｜结语

针对现有的各类城镇化水平拟合方法存在一些缺陷与不足，本文尝试构建自动分段曲线模型进行改革开放以来中国城镇化水平的拟合，并预测2021-2025年中国城镇化发展趋势，得到以下结论：其一，自动分段曲线拟合模型能够有效处理结构变动问题，客观选取分段区间和经验函数，模型拟合精度较高，可解释性强；其二，自动分段曲线模型适用于中国城镇化水平的拟合及预测，为预测城镇化水平提供了新的思路与经验；其三，21 世纪以来，中国城镇化发展进入稳定的高速增长阶段，年均城镇化率提高1.4个百分点，自动分段曲线模型预测2025年中国城镇化率将突破70%，达到71.22%左右。

需要指出的是，将自动分段曲线拟合模型用于中长期预测时，预测精度可能随时期发展而有所下降，这是由于该模型对原始序列进行分段处理，在各区间内使用不同的经验函数拟合，故对未来进行预测时没有利用到原始数据的全部信息，存在一定的信息损失。为解决这一问题，可通过适当调整模型参数以达到更好的长期预测效果。