基于眼动数据的核电厂数字化主控室操纵员认知负荷量化模型研究

戴立操,张美慧,马 莉

(南华大学 人因研究所，湖南 衡阳 421001)

随着技术的发展，核电厂主控室中数字化人机界面(Digital Control System,DCS)逐渐取代传统的模拟显示控制界面。数字化人机界面改变了控制室操纵员信息输入输出方式，从而改变了主控室操纵员认知负荷。本研究利用眼动追踪系统，提出量化数字化主控室操纵员认知负荷水平的方法，对于提高操纵员的绩效水平和核电厂的安全具有重要的研究意义。

Sweller在1988年首次提出认知负荷这一概念，他认为认知负荷就是在特定的作业时间内施加于个体认知系统的心理活动总量[1]。经过几十年的发展，现有的认知负荷主要分为主观测量[2]、任务绩效测量[3]、生理测量[4]和多指标综合测量[5]四种方法。由于眼动追踪技术具有便于佩戴、使用方便、干扰性小等优点[6]，在现有的生理测量方法中眼动追踪技术最为常见。眼动追踪技术开发以来，已广泛用于各个领域，具有巨大的应用价值。在眼动追踪技术发展初始，多用注视时长、注视点的个数等眼动指标对操纵员认知负荷进行测量[7]。随着眼动技术的发展，眼动数据逐渐从定性研究转为定量研究，由此学者提出了注视熵的概念。注视熵包括两种，一种是静止注视熵(Stationary Gaze entropy，SGE)，指量化眼球运动的空间分布，另一种是注视转换熵(Gaze transition entropy，GTE)，指通过转换模式来对注视行为进行评估的一种方法[8-9]。注视熵被提出以来，广泛用于各个领域[10-12](如手术执行、飞行控制和驾驶任务)。与其他眼动指标(如瞳孔直径)相比，注视熵的测量值具有不受外部因素(环境光线和情绪状态)影响的优点[13-14]。

本研究旨在构建基于静止注视熵、注视转移熵、注视点的个数以及注视时长等四项眼动指标的认知负荷量化模型。实验中选择发生概率较高的小破口事故作为事故工况进行模拟实验[15]。在实验过程中操纵员佩戴眼动仪对操作过程的眼动数据进行记录，实验结束后进行NASA—TLX量表的填写和眼动数据的收集。将量表数据与眼动指标进行相关性分析，确定量化模型的可行性，再将测量值Pn与量化模型计算值P进行误差分析，验证模型的准确性。

一 量化模型的构建

基于Diaz-piedra C[9]、Di stasi L L[10]、Shiferaw B A等[11]关于注视熵与操纵员任务负荷相关性的研究以及Lamberts[16]和刘鑫等[6]关于注视时长和注视点个数与操纵员认知负荷之间关系的研究，选取SGE、GTE、单位时间内注视点的个数以及注视时长这四个指标作为构建量化模型的基础。

(一)静止注视熵(SGE)

SGE是对眼球运动的空间分布的一种量化。SGE测量在给定的观看时间内注视位置的不确定性。Leandro等通过记录在三个腹腔镜运动的高保真虚拟模拟过程中的眼球运动，发现当手术任务的难度增大时静止注视熵会随之增加[10]。本研究中将静止注视熵作为量化模型的正相关变量之一。

(二)注视转移熵(GTE)

GTE可以通过眼动的转化模式对注视行为进行评估。GTE是基于当前注视位置，对下一个注视位置的不确定性进行测量。Brook等通过注视熵研究酒精对驾驶行为的影响，发现酒精对注视控制的减弱是通过GTE在上升和下降时段的减少来反映的[11]。本研究将注视转移熵作为量化模型的正相关变量之一。

(三)注视点个数(Fixation Count)

注视点个数是指在单位时间内某个区域中注视点的数量。王葵等发现，注视点的个数与学习者的认知负荷正相关[17]。本研究将注视点个数作为量化模型的正相关变量之一。

(四)注视时长(Fixation Time)

注视时长是指在注视状态下，人的视线在特定区域内的持续注视时间。Privitera等通过研究发现，注视时间越长，认知负荷越大，注视时间与认知负荷之间存在显著正相关的关系[18]。本研究将注视时长占测试总时长的百分比作为量化模型的正相关变量之一。

基于以上的研究分析我们可以得知，静止注视熵、注视转移熵、注视点的个数以及注视时长四项眼动指标与操纵员认知负荷之间存在显性的相关关系，操纵员认知负荷增大的同时，四项指标均会增大。基于这个结论并结合薛耀锋等[19]建立的线上学习的认知负荷量化模型研究，本研究构建的基于注视熵等眼动数据的核电厂数字化主控室操纵员认知负荷量化模型公式为：

P=a×(t/T)×SGE×GTE×N+b

(1)

其中t为注视状态的时长，T为测试总时长、SGE为静止注视熵、GTE为注视转移熵、N为单位时间内注视点的个数、a为相关因子，b为偏差因子。

我们将M作为四项眼动指标的乘积，即：M=(t/T)×SGE×GTE×N。量化模型结构见图1。对于模型的量化主要分为两个部分：眼动数据收集和模型计算[19]。在眼动数据收集部分，将眼动仪记录的眼动数据导入Tobii Pro眼动数据分析软件中，得出四项眼动指标的数据，依据这些数据进行模型的计算。在模型的计算部分，对认知负荷测量值Pn和眼动指标乘积进行回归分析，得出模型的相关因子a以及偏差因子b。

图1 认知负荷量化模型

二 研究方法与实验设计

(一)研究方法

本研究采用主观测量法对操纵员的认知负荷进行测量，所采取的量表为NASA—TLX量表。NASA—TLX量表包括六个维度：脑力负荷、体力需求、时间需求、业绩水平、努力程度和受挫程度，具有使用简单便捷、成本低、主观性强的优点[9]。采用问卷形式，每个问题下有一条10分制的直线，被试者依据自己完成任务时的实际情况对各项进行打分。为确定六个维度的权重，让被试者对六个维度进行两两比较，共组成15对，选出每对中与认知负荷关联更为密切的一项[6]。最终确定六个维度的权重分别为：19.7%、18.7%、14%、22%、17.3%、8.3%。利用SPSS数据分析软件对量表进行信度和效度分析，信度α=0.664，属于可接受范围；效度KMO=0.72，具有较好的效度[20]。本研究采用NASA—TLX量表测量值作为认知负荷测量值Pn，Pn取值范围为1～10。

(二)实验设计

本研究的所有实验均在南华大学人因研究所的M310压水堆核电厂模拟机平台上进行，实验过程中操纵员佩戴Tobii Glass 2.0眼动仪进行眼动数据收集。共有19名被试者参与本次实验，所有被试者均为南华大学在读研究生，被试者视力或矫正视力正常，且具备熟练的操作技术。每位被试者均在一回路的六个屏幕上进行两次操作，分别为正常工况(气机发动机冲转、并网至最小负荷50 MW)和事故工况(small loss of coolant,SLOCA)。每次实验由两位被试者分别对一回路和二回路进行操纵，一回路操纵员(此处操纵员指被试者，下同)佩戴眼动仪收集实验过程中操纵员的眼动数据，实验结束后二者交换位置，再次进行实验。

实验结束后，首先由被试者对本研究提供的NASA—TLX量表[21]进行填写，以对操纵员在任务完成过程中的认知负荷水平进行主观测量；其次，取出眼动仪中的内存卡将其所记录的内容上传至Tobill Pro眼动数据分析软件，在此软件中进行眼动分析，需要选择一张背景图，本实验中所选择的背景图即为一回路操作的六个屏幕，观察被试者在这六个屏幕上的眼球运动轨迹。完成分析后，将所用到的眼动指标的相关数据导出，将所需眼动指标乘积与认知负荷测量值进行相关性分析和方差分析，确定两者之间存在的相关关系，验证模型的可行性。将由量化模型计算出认知负荷计算值，并对认知负荷测量值进行误差分析，验证模型的准确性。

三 量化模型的可行性和准确性分析

(一)模型的可行性分析

将实验过程中所采集到的眼动数据上传至Tobii Pro眼动数据分析软件进行分析处理，可以直接得到任务完成过程中的注视点个数以及注视状态时长两个指标。而SGE和GTE这两个指标则需要通过计算才能得到。为得到SGE和GTE的值，首先我们将兴趣区域定义为1900PX×1000PX的空间，并将其划分为190个100PX×100PX的空间状态[11]；再利用Python对注视点的位置进行编程，得出190个状态空间内各自的注视点个数；最后对SGE[22]和GTE[23]的计算公式进行编程，得出任务完成过程中操纵员的SGE和GTE。

(2)

(3)

其中，x表示任务过程的一组注视，n表示被注视所占据的空间状态的数量，i表示占用的空间状态，Pi表示第i个空间状态内注视的比例，P(i|j)表示从状态i转移到状态j的概率，i≠j。

对注视状态总时长(t)、单位时间内注视点的个数、SGE、GTE值进行收集和整理，将数据按照公式计算出四项眼动指标的乘积M，同时将NASA—TLX量表按照权重进行计算，得出认知负荷测量值Pn，后续将利用SPSS数据分析软件对Pn和M之间的相关关系进行分析。所得眼动指标乘积M与认知负荷测量值Pn如表1和表2所示。

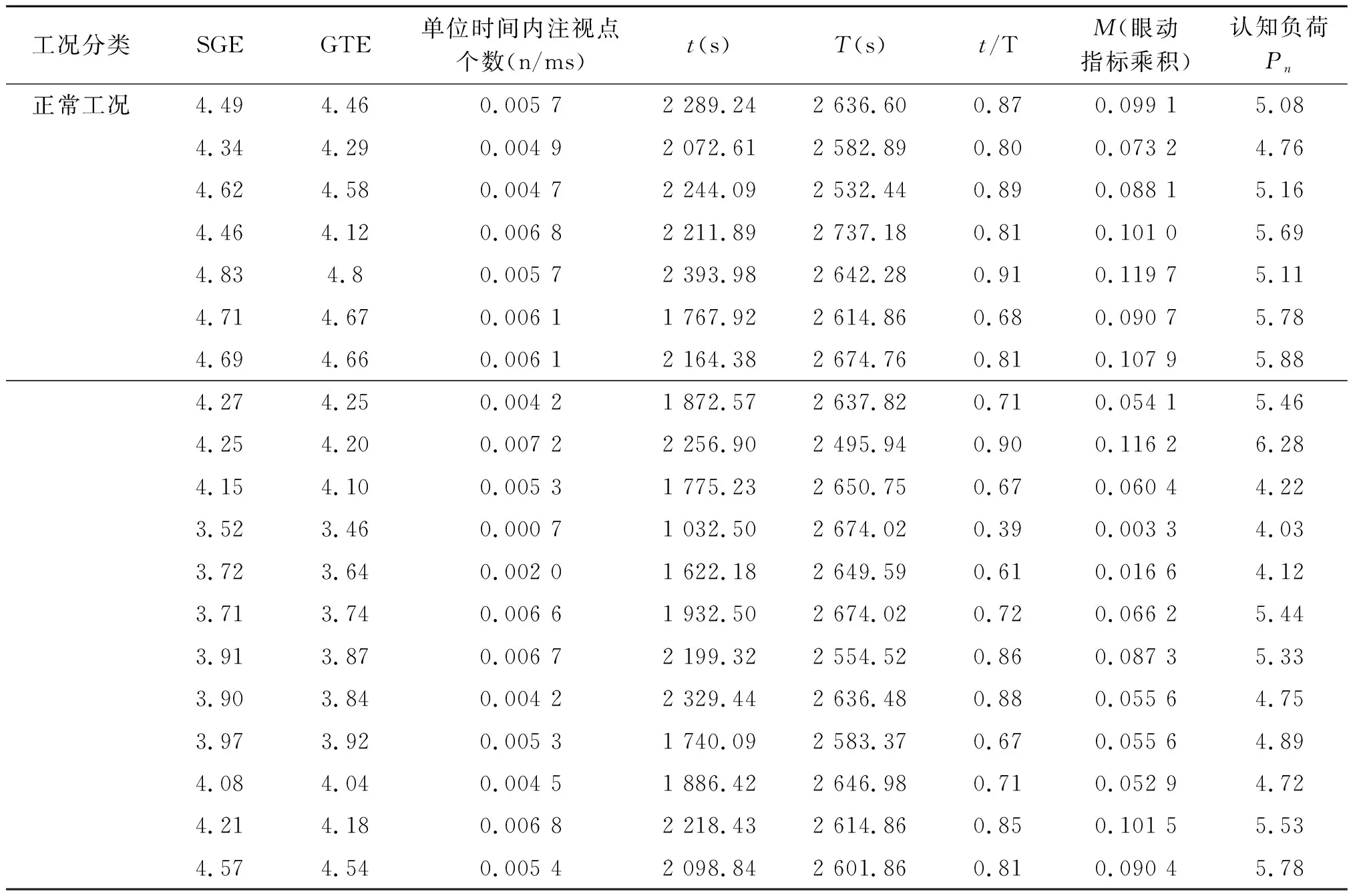
表1 正常工况下的M值和Pn值

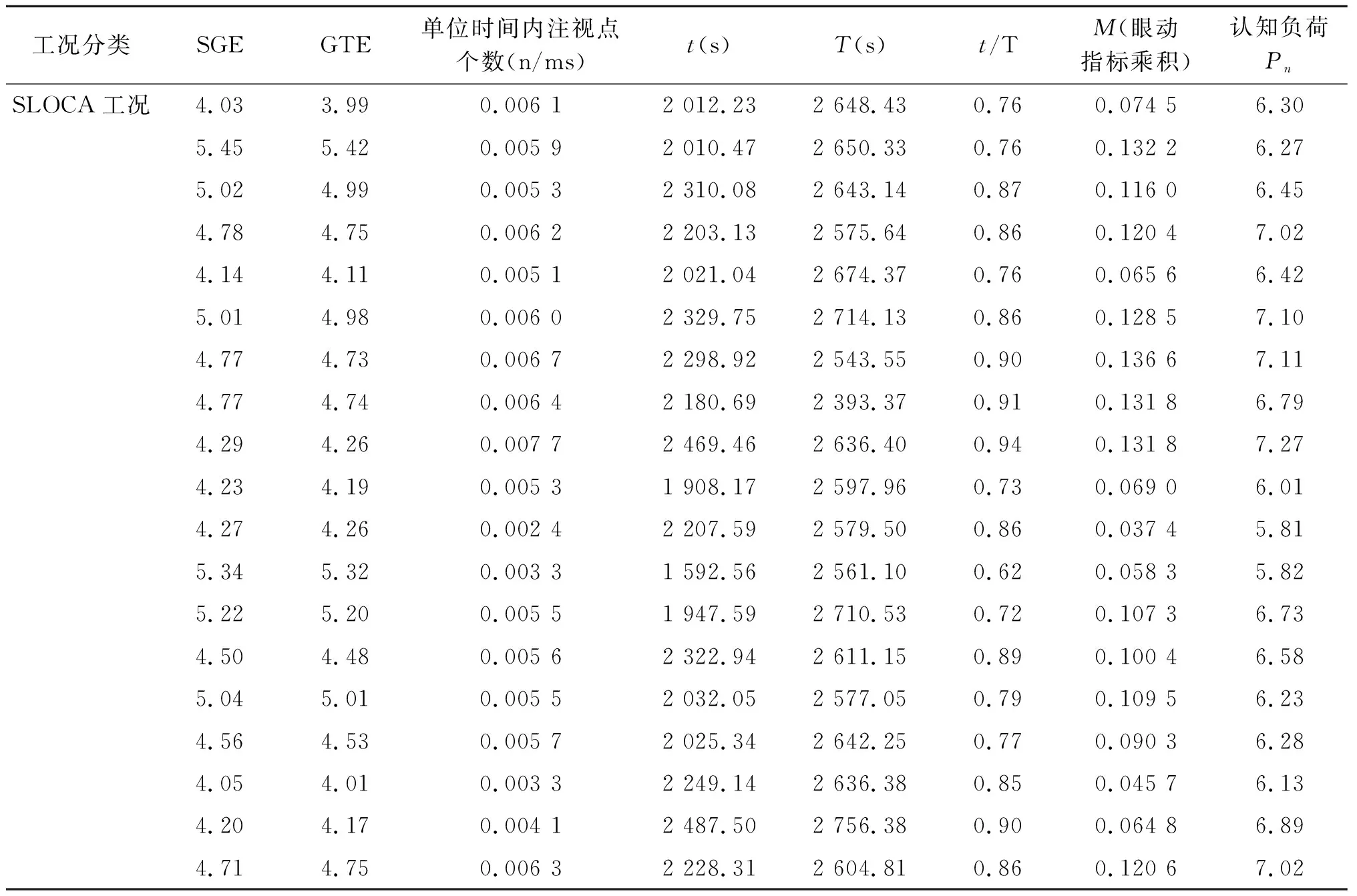
表2 事故工况下的M值和Pn值

利用SPSS数据分析软件对正常工况下操作阶段操纵员认知负荷测量值Pn和眼动指标的乘积M进行相关性分析，相关系数为0.790(P<0.05)，这表明眼动指标乘积M与认知负荷测量值Pn之间存在显著的正相关关系，如表3所示。对认知负荷测量值Pn和眼动指标的乘积M进行线性回归分析，得到a与b的值，结果如表4所示。

表3 正常工况下Pn与M的相关性分析

表4 正常工况下Pn与M的线性回归分析

①表示在1%的统计水平上显著。

由表4可知，F(1，17)=28.281(P<0.05)，这表明认知负荷测量值Pn与眼动指标乘积M之间存在线性相关的关系。根据表4，可以得出a=15.559，b=3.979，得出正常工况下操作阶段操纵员认知负荷的量化公式为：

P=15.559×(t/T)×SGE×GTE×N+3.979

(4)

利用SPSS数据分析软件对事故工况下操作阶段操纵员认知负荷测量值Pn和眼动指标的乘积M进行相关性分析，相关系数为0.722(P<0.05)，这表明眼动指标乘积M与认知负荷测量值Pn之间存在显著的正相关关系，如表5所示。依据相关性分析结果，对认知负荷测量值Pn和眼动指标的乘积M进行线性回归分析，得到a与b的值，结果如表6所示。

表5 事故工况下操作阶段Pn与M的相关性分析

表6 事故工况下操作阶段Pn与M的线性回归分析

由表6可知，F(1，17)=18.535(P<0.05)，这表明认知负荷测量值Pn与眼动指标乘积M之间为线性相关的关系。根据表6，可以得出a=10.037，b=5.566，故事故工况下操作阶段操纵员认知负荷量化公式为：

P=10.037×(t/T)×SGE×GTE×

N+5.566

(5)

由上可知，这两种工况中认知负荷测量值Pn与眼动指标乘积之间均存在显著的线性相关关系，故基于注视熵等四项眼动数据的认知负荷量化模型具有可行性。

(二)模型的准确性分析——误差分析

根据两种工况下的量化模型，对操纵员认知负荷进行计算，计算结果如表7所示。正常工况下操纵员的认知负荷平均值为5.16，事故工况下操纵员的认知负荷平均值为6.54。

表7 两种工况下操纵员的认知负荷计算值

为对量化模型的准确性进行验证，对Pn与P的平均相对误差进行分析，计算如公式(6)所示。

Re=∑(|Pn-P|)/n

(6)

其中，Re为平均相对误差，∑(|Pn-P|)为Pn与P的相对误差绝对值之和，n为Pn与P的组数。Re值越小，模型准确性越高。

Pn与P的分布情况如图2和图3所示。得到正常工况下Re为0.29，事故工况下Re为0.25。此数值较小，表明此模型的准确度较高。

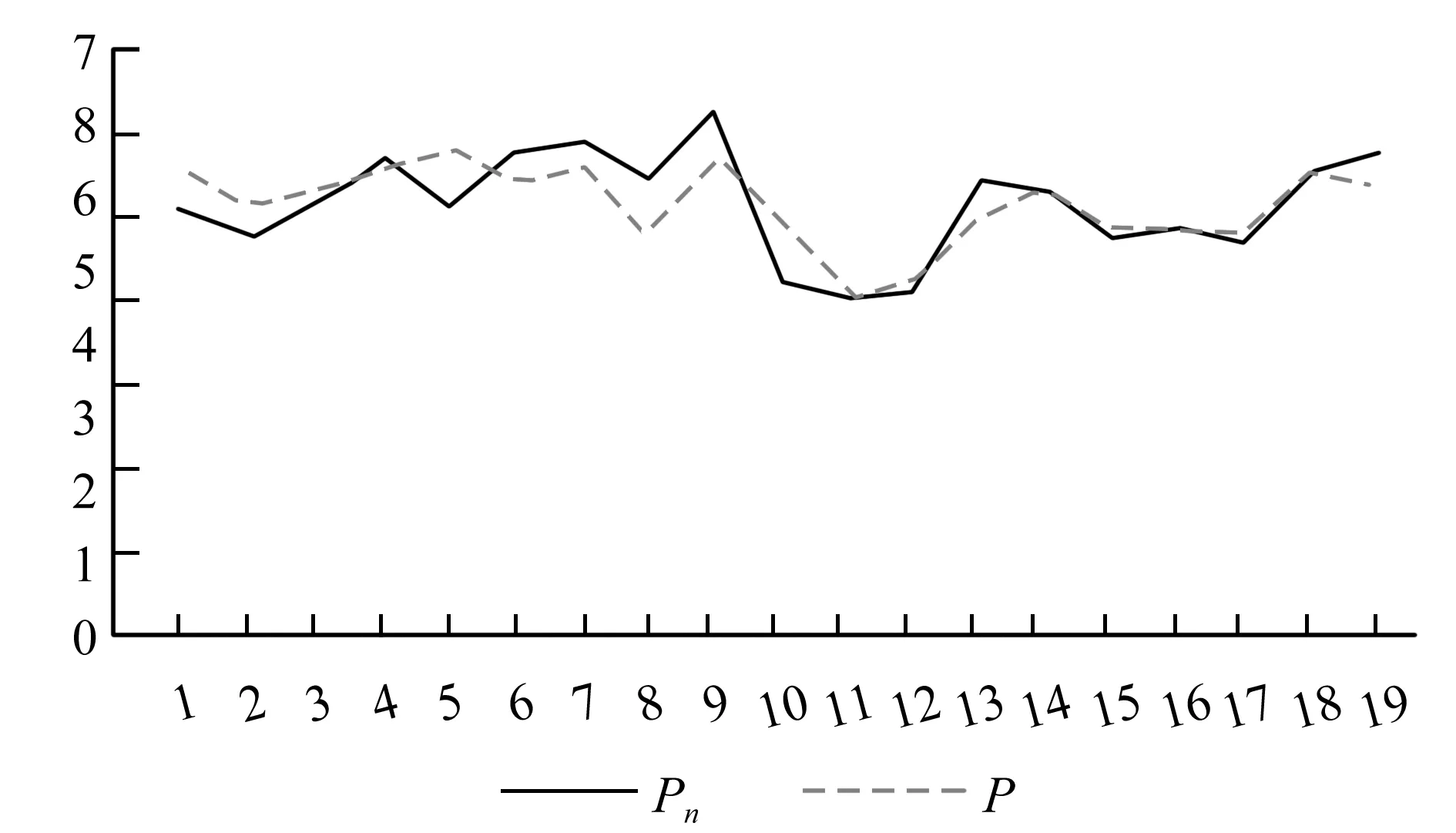
图2 正常工况下P与Pn的分布图

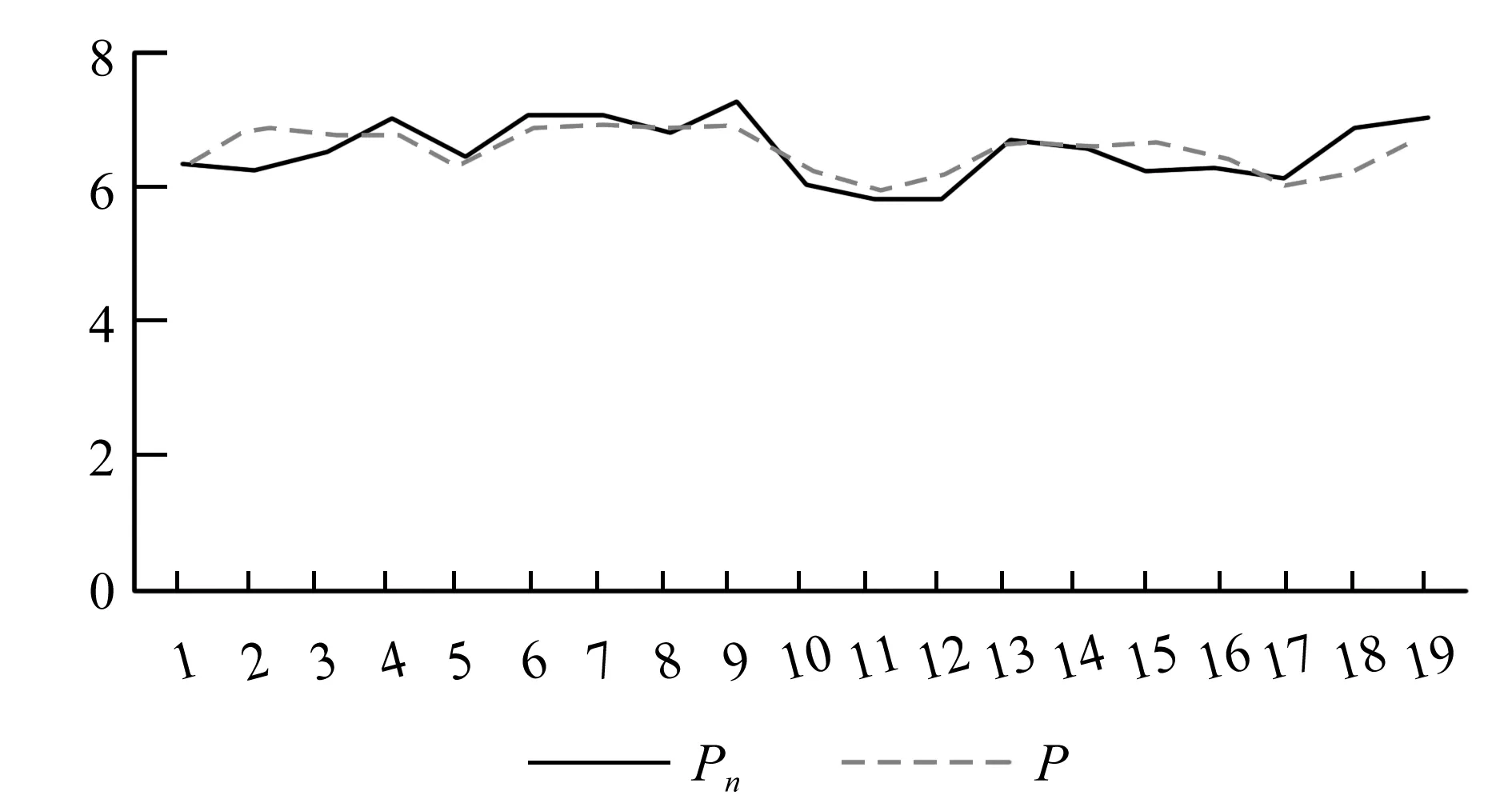
图3 事故工况下P与Pn的分布图

四 结果与讨论

本研究旨在基于注视熵等四项眼动指标构建出核电厂数字化主控室操纵员认知负荷的测量模型。对数据进行分析，得出以下结论：

第一，正常工况下对操纵员操纵阶段进行分析得出，认知负荷测量值Pn和眼动指标的乘积M的相关系数为0.790(P<0.05)，F(1，17)=28.281(P<0.05)，表明Pn与M之间存在线性相关关系。a=15.559，b=3.979，故正常工况下操作阶段操纵员认知负荷的量化公式为：P=15.559×(t/T)×SGE×GTE×N+3.979。

第二，事故工况下对操纵员操纵阶段进行分析得出，认知负荷测量值Pn和眼动指标的乘积M的相关系数为0.722(P<0.05)，F(1，17)=18.535(P<0.05)，表明Pn与M之间存在线性相关关系。a=10.037，b=5.566，故事故工况下操作阶段操纵员认知负荷量化公式为：P=10.037×(t/T)×SGE×GTE×N+5.566。

第三，对认知负荷测量值Pn与计算值P的相对误差进行分析，得出两种工况下Pn与P的平均相对误差分别为0.29与0.25，误差较小，模型的准确度较高。

本研究发现认知负荷测量值与SGE、GTE、注视时长以及单位时间内注视点的个数共四项眼动指标的乘积显著正相关。这表明由此四项眼动数据的乘积所构成的量化模型对操纵员认知负荷进行研究具备可行性，可以在一定程度上反映核电厂数字化主控室操纵员的认知负荷水平。在此基础上，对模型进行误差分析，证明了模型具备较高的准确度。后续将会对本研究进行完善，扩大实验范围和事故种类，可以结合更多的眼动数据以及图像识别、疲劳检测和脑电波技术等建立更准确的认知负荷量化模型，找寻一种能对核电厂操纵员的操纵状态进行不间断评估的方法，为核电厂的安全提供保障。