基于改进型全维观测器的BLDC无传感器控制
顾嘉宁,鲁文其,邹积浩,宿向辉,朱其新
(1.浙江理工大学机械与自动控制学院,浙江 杭州 310000;2.苏州科技大学机械工程学院,江苏 苏州 215009)
0 引言
无刷直流电机因其结构简单、可靠性高、功率密度大和成本较低等优点而被广泛应用到了军事、工业和民用等领域[1-3],但位置传感器的设置限制了其在一些敏感场合的应用,如医疗领域的呼吸机、军事领域的小型飞行器和导弹等,因此去掉位置传感器,采用无传感器的控制技术,成为了当前电机控制领域研究的一个热点。目前,常用的无位置传感器估计方法有反电势法[4]、电感法[5]、磁链观测法[6]、状态观测器法[7-9]和智能控制算法[10-12]等,其中,应用最为广泛的是反电势法[13-17]。文献[18]提出了一种重构中性点的端电压法估算反电势,同时采用基于数学模型的开环补偿对滤波引起的相位延迟进行补偿,但是该方法参数敏感度较高且鲁棒性较差,容易因干扰引起误差。文献[19]提出了基于定子绕组电感法的启动方法,采用将检测脉冲电压通入定子绕组,以检测对靠近转子的定子绕组电感值的影响,经过相同检测脉冲电压作用后,出现大小不同的响应电流值,以此方法实现转子初始位置检测。但是该方法检测脉冲电压的通入,会引起转子的振动,产生较大的噪音,同时由于定子绕组绕组电感的存在,电流在上升和下降时存在时间延迟,引起转矩脉动。而利用观测器直接获得转子位置换相点的方法因其电路简单、应用范围广,在无刷直流电机无传感器控制应用中取得了较好的效果,如全维观测器、扩张状态观测器、卡尔曼观测器和龙伯格观测器等[20-23]。文献[24]构建了无刷直流电机反电动势自适应滑块观测模型,然而未能解决滑模观测器的抖振和转子位置误差补偿问题。文献[25]设计了一种双扩展卡尔曼观测器,利用带有噪声的输入信号以实时估计无刷直流电机状态和参数,但是该方法对电机模型是强依赖的,若考虑电机参数的扰动,则系统鲁棒性较低。
全维状态观测器是一种算法简单的线性观测器,可以在一定程度上解决系统参数变化、扰动等带来的影响。文献[26]提出了基于反电势观测器的电机直流母线电压和端电流传感器的无位置传感器控制算法,保证了对无刷直流电机在全速范围内速度和位置的正确估计,但该方法在启动时仍存在较大延迟。文献[27]提出了一种基于全维状态观测器的线反电动势估计算法,线反电动势作为位置变量进行在线估计,进而求出所需的转速和转子位置信息,但该方法与传统观测器类似,无法较好地解决延迟问题。
为了解决传统全维观测器响应能力差的问题,本文对传统全维观测器的数学模型进行推导分析并改进,提出了一种新的全维观测器。为了验证算法的正确性进行了理论分析与实验测试,下面分别对其进行阐述。
1 基于传统全维观测器的转子速度估算
BLDC在三相静止参考坐标系下的线电压方程为
(1)
R为定子电阻;L为定子电感;eab、ebc为在三相静止坐标系下的线反电势;iab、ibc为在三相静止坐标系下的定子电流的差;uab、ubc为在三相静止坐标系下的线电压。
整理式(1)得电机的动力学状态方程式为

(2)

为了获得反电动势,根据式(2)可建立一个传统全维状态观测器,即

(3)
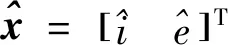
由式(2)~式(3)得
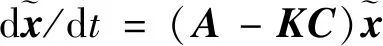
(4)

(5)
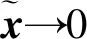
最后得到传统全维观测器的电流i、反电势e计算公式为
(6)
估算出反电动势后,通过锁相环(PLL)控制,系统根据式(7)~式(8)可计算出无刷直流电机最终的转子速度和位置信息。
(7)

(8)

根据以上分析得到传统全维观测器原理如图1所示。
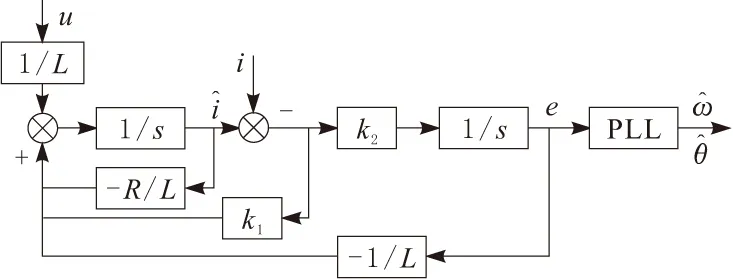
图1 传统全维观测器原理
2 基于改进型全维观测器的转子速度估算
采用传统全维观测器对转子速度进行估算可以提高系统的动态响应性能和鲁棒性,然而变速的时候,实际反电势会很快作出响应,但用观测器估算得到的反电势,其响应会有延迟,最终导致设计的系统出现了不稳定现象。对此,本文对图1所示的全维观测器进行改进,构建改进型全维观测器为
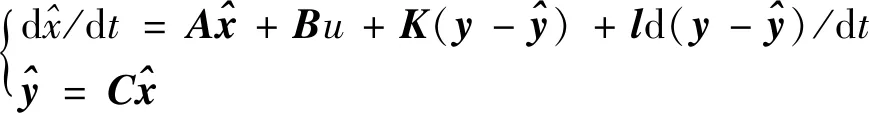
(9)
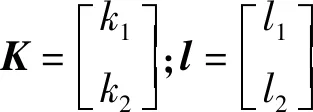
由式(2)和式(9)可得

(10)

(11)
根据期望极点α、β,以及观测器的期望特征方程(11)可得
(12)
假设α=β,设计l1=k1,l2=k2,则可得状态反馈系数值为
(13)
根据式(13)可以得出
(14)
估算出反电动势后,转子速度和转子位置同样采用式(7)和式(8)计算得到。
根据以上分析得到改进型全维观测器原理如图2所示。而无位置传感器控制系统原理如图3所示,其由速度环PI调节器、电流环PI调节器、PWM调制、换相逻辑控制、三相逆变器、电流检测、无刷直流电机、锁相环系统和改进型全维观测器等组成,ωref为给定转速。

图2 改进全维观测器原理
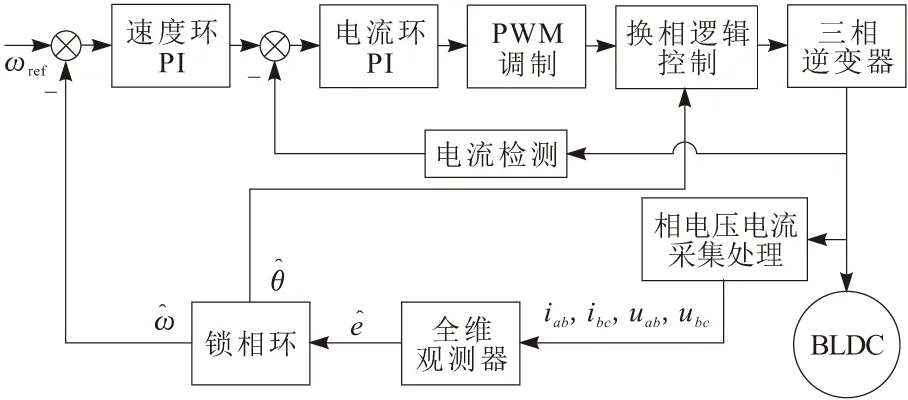
图3 BLDC无传感器控制系统原理
3 实验验证
为了验证本文方案的正确性和优越性,设计了试验平台,分别对传统和新型全维观测器算法进行性能的对比分析。其中,试验平台如图4所示,该平台由上位机、涡轮风机(BLDC)和驱动器等组成。电机主要参数如表1所示。

图4 无刷直流电机驱动测试平台

表1 无刷直流电机主要参数
为了验证本文方法的正确性及其在提高电机启动时响应速度方面的优越性,从给定恒定速度为1 000 r/min和20 000 r/min的空载启动情况下,分别对采用传统全维观测器控制的系统和采用改进型全维观测器控制的系统进行了对比测试。
图5是给定速度1 000 r/min空载启动时,传统和改进全维观测器控制系统的对比波形。由对比波形可知,采用传统全维观测器控制的系统大约经过1.21 s运行到了给定速度,且最高速度为1 312.8 r/min,而采用改进型全维观测器控制的系统明显比采用传统全维观测器控制的系统更快(约 0.92 s)到达给定速度, 同时系统超调明显减小, 最高速度只有1 203.5 r/min;转子位置和反电势都由稀疏到密集,且采用传统全维观测器控制的系统的转子位置和反电势与实际存在较大延迟,而采用改进型全维观测器控制的系统的转子位置和反电势与实际几乎重合;稳态过程,采用传统全维观测器控制的系统最高速度为1 041.3 r/min,最低速度为956.1 r/min,稳态误差为8.52%,而采用改进型全维观测器控制的系统抖振明显比采用传统全维观测器控制的系统小,最高速度为1 009.7 r/min,最低速度为978.4 r/min,稳态误差为3.13%。

图5 给定速度1 000 r/min且空载情况下的试验测试
图6是给定速度20 000 r/min空载启动时,传统和改进全维观测器控制系统的对比波形。由图6可知,启动过程,采用传统全维观测器控制的系统大约经过1.35 s运行到了给定速度,且最高速度为20 658.3 r/min,而采用改进型全维观测器控制的系统明显比采用传统全维观测器控制的系统更快(约1.03 s)到达给定速度,同时系统超调明显减小,最高速度只有20 509.2 r/min;转子位置和反电势都由稀疏到密集,且采用传统全维观测器控制的系统的转子位置和反电势与实际存在较大延迟,而采用改进型全维观测器控制的系统的转子位置和反电势与实际几乎重合;稳态过程,采用传统全维观测器控制的系统最高速度为20 227.8 r/min,最低速度为19 794.2 r/min,稳态误差为2.168%,而采用改进型全维观测器控制的系统抖振明显比采用传统全维观测器控制的系统更小,最高速度只有20 107.4 r/min,最低速度为19 872.3 r/min,稳态误差为1.18%。

图6 给定速度20 000 r/min且空载情况下的试验测试
为了进一步验证本文方法的正确性及其在提高电机启动时响应速度方面的优越性,本文又从给定速度为1 000 r/min和20 000 r/min的满载启动情况下,分别对采用传统全维观测器控制的系统和采用改进型全维观测器控制的系统进行了对比测试。
图7是给定速度1 000 r/min满载启动时,传统和改进全维观测器控制系统的对比波形。对比波形可知,采用传统全维观测器控制的系统大约经过1.68 s运行到了给定速度,且最高速度为1 216.8 r/min,而采用改进型全维观测器控制的系统明显比采用传统全维观测器控制的系统更快(约1.37 s)到达给定速度,同时系统超调明显减小,最高速度只有1 143.5 r/min;转子位置和反电势都由稀疏到密集,且采用传统全维观测器控制的系统的转子位置和反电势与实际存在较大延迟,而采用改进型全维观测器控制的系统的转子位置和反电势与实际几乎重合;稳态过程,采用传统全维观测器控制的系统最高速度为1 025.3 r/min,最低速度为973.6 r/min,稳态误差为5.17%,而采用改进型全维观测器控制的系统抖振比采用传统全维观测器控制的系统更小,最高速度只有1 005.8 r/min,最低速度为991.4 r/min,稳态误差为1.44%。

图7 给定速度1 000 r/min且满载情况下的试验测试
图8是给定速度20 000 r/min满载启动时,传统和改进全维观测器控制系统的对比波形。由对比波形可知,启动过程,采用传统全维观测器控制的系统大约经过1.98 s运行到了给定速度,且最高速度为20 518.2 r/min,而采用改进型全维观测器控制的系统明显比采用传统全维观测器控制的系统更快(约1.59 s)到达给定速度, 同时系统超调减小,最高速度为20 376.1 r/min;转子位置和反电势都由稀疏到密集,且采用传统全维观测器控制的系统的转子位置和反电势与实际存在较大延迟,而采用改进型全维观测器控制的系统的转子位置和反电势与实际几乎重合;稳态过程,采用传统全维观测器控制的系统最高速度为20 147.8 r/min,最低速度为19 864.2 r/min,稳态误差为1.02%,而采用改进型全维观测器控制的系统抖振明显比采用传统全维观测器控制的系统更小,最高速度只有20 075.4 r/min,最低速度为19 932.5 r/min,稳态误差为0.72%。

图8 给定速度20 000 r/min且满载情况下的试验测试
综上所述,采用改进型全维观测器控制的系统,无论在空载启动还算是满载启动情况下,都比采用传统全维观测器控制的系统更快地到达给定速度,且在稳态时稳态误差更小。由此可知,采用改进型全维观测器控制的系统,能提高系统的动态响应能力、减小启动超调和稳态抖振。
4 结束语
为了解决传统全维观测器存在的启动变速响应慢、超调大等问题,本文基于观测器机理分析,引入了反馈增益,提出了一种新型全维控制器转子速度估算方法。实验结果表明:与传统全维观测器相比,新型全维观测器将原来单一的比例环节改进为微分加比例调节,使系统对转子的估算速度能够较好地跟随实际转速的变化而变化,提高了系统的动态响应能力,并减小了稳态抖振和超调,增加了系统稳定性。基于改进型全维观测器的BLDC无传感器控制系统能够提高系统整体的辨识收敛速度、动态响应能力和稳定性,具有一定的实用性。

