参数不确定条件下基于I&I的异步电机鲁棒控制新方法
王鹍鹏,张 磊
(1.黑龙江中医药大学附属第一医院设备科,黑龙江 哈尔滨 150040;2.哈尔滨工业大学机械工程学院,黑龙江 哈尔滨 150001)
0 引言
异步电动机(induction motor,IM)具有多变量、强耦合和非线性等特征,使其难于进行精确、稳定控制。目前,已提出各种IM鲁棒控制方法,如模糊控制[1-2]、自适应控制[3]、神经网络控制[4]、最优控制[5]和滑模控制(sliding mode control,SMC)[6-7]等。
浸入与不变性(immersion and invariance,I&I)理论是进行鲁棒控制器设计的一种新方法,尤其适用于具有参数不确定性的系统[8-9]。I&I方法的基本思想是根据系统浸入对目标系统的稳定性进行重构,并基于系统动力学实现控制,从而得到期望的输出响应[10]。大量工程应用结果表明,当存在系统参数不确定性和故障的情况下,基于I&I的控制方法具有较高的鲁棒性[11-14]。
文献[11]比较了基于I&I和SMC的2种控制器性能,根据实际的驾驶场景,以某型汽车为例在MATLAB/Simulink中对闭环系统进行了仿真,实验结果验证了基于I&I算法控制器的有效性和鲁棒性;在考虑不确定性和执行器未知故障条件下,文献[12]提出了基于I&I理论的鲁棒自适应航天器姿态控制策略,结果表明,当存在不确定故障时,基于I&I的故障鲁棒自适应姿态控制器优于传统的自适应控制器;文献[13]研究了I&I理论在磁悬浮系统的稳定控制问题中的应用;文献[14]针对非线性刚度关节,基于I&I理论设计了控制器,并与比例微分控制器进行了对比,说明了在参数存在不确定性的情况下,I&I方法具有明显的优势。
本文针对不确定参数存在条件下异步电机难以精确动态控制的问题,提出一种基于I&I理论的鲁棒控制新策略。首先,基于IM系统动力学和I&I基本原理,在以下2种故障工况下,利用补偿器设计一种考虑故障的鲁棒控制律:
a.由于电机内部发热引起的转子绕组逐渐增加,考虑到趋肤效应的存在,允许转子绕组在其标称值附近有100%的变化。
b.负载转矩的连续变化。
然后,利用I&I的基本原理证明了当存在参数不确定性和故障时,本文所提出的控制律仍可使电机状态轨迹信号有效跟踪期望的参考信号,并利用Lyapunov稳定性分析证明了控制律渐近稳定性。最后,通过仿真实验说明了本文所提出的鲁棒I&I控制方法的有效性。
1 IM模型及I&I基本原理
1.1 IM系统模型
不计机械摩擦条件下,同步旋转坐标系(d-q系)中IM的两相等效状态空间修正模型为
(1)
x1和x2分别为转子转速ω和转子磁通Φr;x3和x4分别为定子电流矢量分量isd和isq;u1和u2分别为控制输入,即定子电压矢量的分量Vsd及Vsq;μ和β为常数。参数a1~a6可由式(2)确定,即
(2)
式(2)中的各参数定义为
(3)
Ls、Lr、Rs、Rr分别为定子/转子的电感和电阻;J为转动惯量;np为极对数;Mi为互感;τrN为τr的额定值(名义值),即τrN=Lr/RrN,RrN为转子电阻额定值;τ1N为τ1的名义值,即当τ1定义式中的Rr取值为RrN时的值。
进一步,引入如下假设:
假设1,电机存在故障。本文指定电机在运行过程中存在2种主要故障。
a.渐变故障,即转子电组逐渐增大,且在其标称值附近存在100%变化范围。
b.意外故障,即负载转矩出现连续变化。
依据假设,采用式(4)对进行转子电阻修正。
Rr=RrN+RrN[1-exp(-1.2t)]
(4)
假设2,负载转矩Tr和转子电阻Rr未知,但二者的值具有已知上限。
1.2 I&I基本原理
考虑系统:

(5)
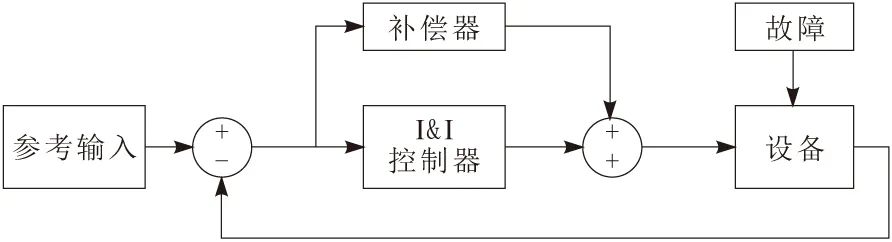
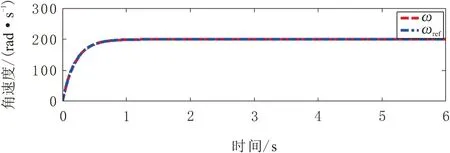
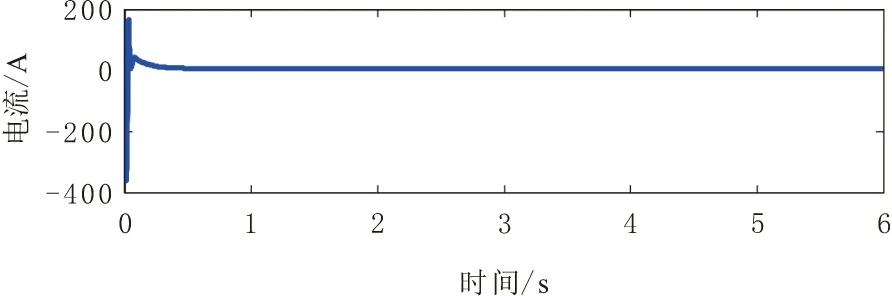
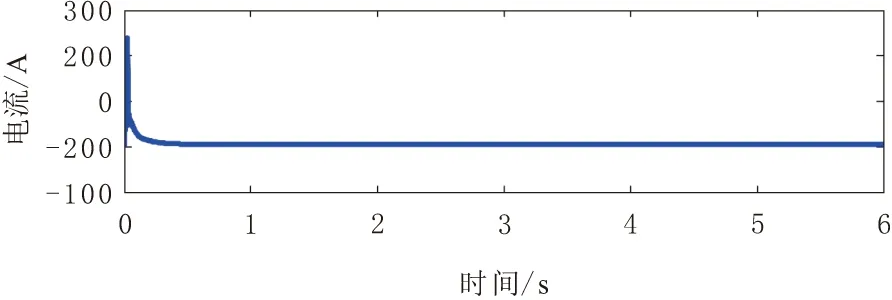
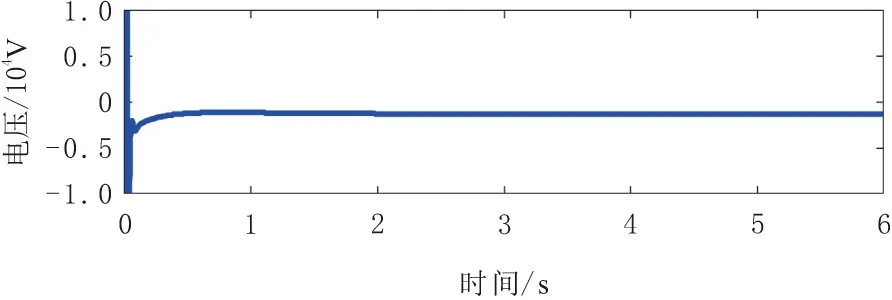
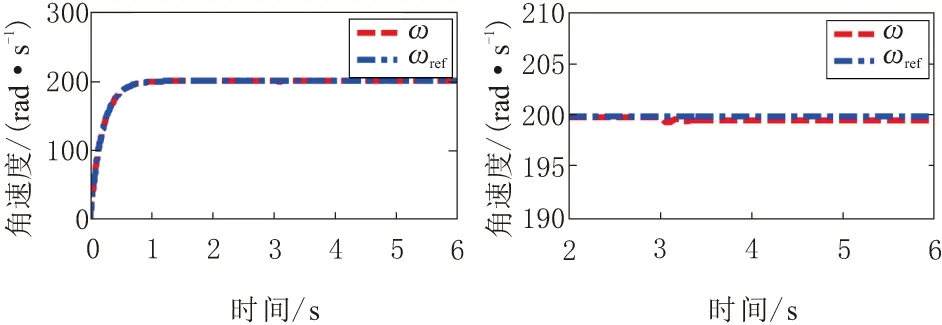
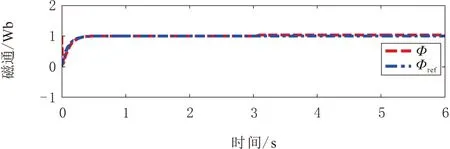
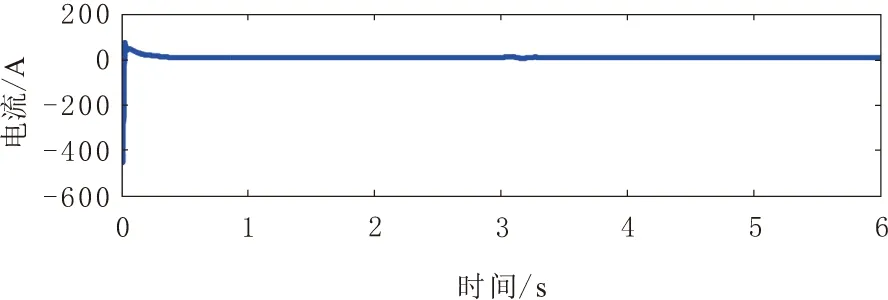
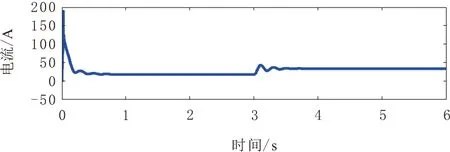
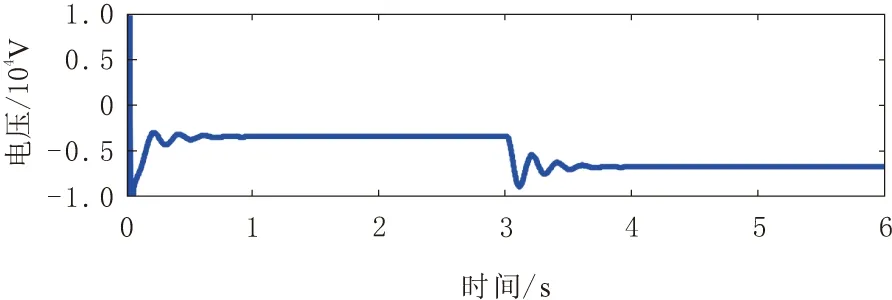
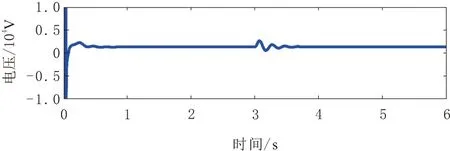
x∈Rn,u∈Rm(n,m∈N),系统的稳定平衡点为x*∈Rn。若p a.(H1)(目标系统稳定条件)。 (6) ξ∈Rp。式(6)所示系统在ξ*∈Rp和x*=π(ξ*)处具有全局渐近稳定平衡点。 b.(H2)(浸入条件)。 对于所有ξ∈Rp,有 (7) c.(H3)(隐式流形条件)。 存在如下集合: M={x∈Rn|Φ(x)=0} (8) M={x∈Rn|x=π(ξ),∃ξ∈Rp} (9) d.(H4)(流形吸引性和轨迹有界性)。 若以下系统的所有轨迹有界: (10) (11) 且满足 (12) 则x*是如下闭环系统的全局渐近稳定平衡点: (13) 本文控制策略分为2个步骤。首先,假设系统无不确定因素(健康状态),设计了一般的I&I控制器;然后,为补偿不确定因素的影响,包括负载转矩和转子电阻的变化(故障状态),考虑不确定性的上限,对控制信号进行校正。 根据式(1)中的IM系统动力学模型,当所有系统参数已知时,建立其控制律。 首先,给出系统的跟踪误差为 (14) r1和r2为相应的参考值。根据误差表达式,建立系统误差动力学方程为 (15) 进一步,依据I&I的基本原理,扩展实际IM系统与目标系统之间的映射关系为 (16) 映射π3(η1,η2)和π4(η1,η2)需要根据I&I基本定理的条件(H1)~(H4)进行确定。 a.(H1)的验证。 (17) (18) 根据式(15)和式(17),可得 (19) 易见,η=(0,0)为上述目标系统的唯一全局渐近稳定平衡点。 b.(H2)的验证。 由式(7)导出的映射π(·)为 (20) c.(H3)的验证。 根据式(8),存在集合为 (21) d.(H4)的验证。 由式(10)和式(11),可构造 (22) 进一步,依据式(15),在忽略负载转矩和转子电阻的变化时,可以得出 (23) 参数γ为正常数,对其值进行调整可以使系统满足渐近稳定性。与式(18)相类似,定义目标系统为 (24) 同样地,由式(24)定义的ξ1和ξ2的动力学行为具有渐近稳定性。 在已知系统参数并假设不确定性存在的情况下,将本文所提出的鲁棒控制方法应用于IM。假设负载转矩和转子电阻具有不确定性,但二者的上界已知,设计一种新的控制器以实现IM的鲁棒控制,如图1所示。 图1 I&I控制器设计流程 依据假设的2类故障,将动力学方程(24)进行补偿修正,即 (25) 定义控制律为 (26) 基于式(25)的补偿器及控制律(26),得出前述2类故障下的控制律为 (27) 进一步,定义的Lyapunov候选函数为 (28) (29) 上述过程在故障和不确定条件下,利用补偿器得出新的鲁棒控制器,并基于Lyapunov稳定性分析,证明了控制律稳定性[14]。 注意到,使用不连续函数(如式(26)中的符号函数)时,会导致系统出现抖振现象。为此,可利用双曲正弦函数对式(26)中的控制信号进行修正,即 (30) 通过MATLAB(R2014a)/Simulink(V8.3)平台,仿真验证本文所提出的鲁棒I&I控制律的有效性,定步长为8.5×10-6s,算法为ode3,仿真时间为6 s。IM(1.5 kW)采用笼型转子(220~380 V)和50 Hz电源,其标称电气和机械参数如表1所示。转子角速度、转子磁通和负载转矩的参考值分别为ωref=200 rad/s,Φref=1 Wb和TrN=5 N·m。 表1 仿真实验中IM的标称参数 首先,假设负载转矩和转子电阻为固定值,IM系统不存在不确定性。转子转速、转子磁链、定子电流/电压直轴分量和交轴分量的轨迹控制信号如图2~图7所示。可以看出,转子角速度和转子磁链可以很好地跟踪参考信号。 图2 健康状态下转子角速度输出轨迹 图3 健康状态下转子磁通输出轨迹 图4 健康状态下定子电流直轴分量输出轨迹 图5 健康状态下定子电流交轴分量输出轨迹 图6 健康状态下定子电压交轴分量输出轨迹 图7 健康状态下定子电压直轴分量输出轨迹 其次,为验证本文控制方法的鲁棒性,在考虑干扰的情况下进行了仿真。所施加的扰动为:在3 s时的负载转矩从其额定值5 N·m变为10 N·m(如图8所示),转子电阻变化为Rr=RrN+RrN[1-exp(-1.2t)]。 图8 负载转矩的变化 图9~图14给出了故障状态下转子角速度、转子磁链、定子电流/电压的直接分量和正交分量的输出轨迹。图15显示了脉冲参考信号下采用本文控制方法的跟踪性能。可以看出,即使存在外部干扰时,利用本文所提出的鲁棒I&I控制方法,IM转子角速度和转子磁链也能够较好地跟踪参考值,从而验证了本文方法的鲁棒性。最后,在相同条件下,将本文方法与SMC和磁场定向控制(FOC)方法[15]的性能进行了比较,不同方法下的转子角速度输出轨迹如图16所示。结果表明,与其他方法相比,本文方法具有更为良好的鲁棒性。 图9 故障状态下转子角速度输出轨迹 图10 故障状态下转子磁通输出轨迹 图11 故障状态下定子电流直轴分量输出轨迹 图12 故障状态下定子电流交轴分量输出轨迹 图13 故障状态下定子电压直轴分量输出轨迹 图14 故障状态下定子电压交轴分量输出轨迹 图15 脉冲参考信号下的转子角速度跟踪轨迹 图16 不同控制方法下(鲁棒I&I、SMC与FOC)的 本文基于I&I理论,提出了一种在参数不确定情况下IM的鲁棒控制新方法。由于IM系统具有明显的非线性和多变量动态特性,因此,本文首先在考虑负载转矩和转子电阻变化导致的不确定性的前提下,通过设计补偿器对IM的系统动力学模型进行了修正;然后,依据I&I基本原理设计了一种新的鲁棒控制律,并基于Lyapunov稳定性定理,对所提出的鲁棒控制器的稳定性进行了证明;最后,利用仿真实验验证了本文控制方法的有效性。结果表明,在故障情况下,IM转子角速度和转子磁链都能完全跟踪其参考值,且负载转矩、转子电阻的变化不会影响电机输出轨迹的跟踪效果。同时,当参考信号类型变化时,采用本文方法也可使电机输出信号具有良好的跟踪效果。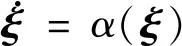



2 鲁棒I&I控制设计及其在IM中的应用
2.1 健康状态
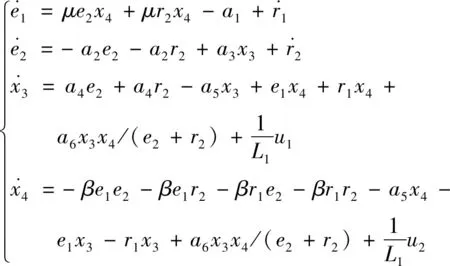


2.2 故障条件(参数不确定)
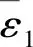

3 实验结果及分析






4 结束语

