甲醇微小尺度燃烧反应动力学模型的简化和优化

张 鹏，倪计民，石秀勇

（同济大学汽车学院，上海 201804）

微型能源系统可采用燃烧的方式为微电子机械设备供能，因此，微小尺度燃烧引起了众多学者的关注［1-3］。甲醇是一种清洁的液体燃料，成本低廉，原料广泛，易于采购，较气体燃料具有能量密度高、便于储存等优点，是微能源系统的理想燃料［4］。然而，相对于内燃机、锅炉等的大尺度燃烧，甲醇在微小尺度燃烧器中的燃烧较为复杂，存在燃料驻留时间短、热损失大及自由基易淬灭等缺点［5-6］。因此，研究适用于微小尺度燃烧条件下的甲醇动力学模型，对于深入研究甲醇在微小尺度燃烧器中的燃烧过程，优化甲醇微小尺度燃烧器结构、提高燃烧稳定性和燃烧效率等具有重要意义。

学者们针对甲醇燃烧反应动力学模型开展了大量研究。基于激波管实验，Bowman［7］首次构建了甲醇的详细燃烧动力学模型，该模型含有14种组分、28个基元反应，能够在高温范围内准确预测甲醇滞燃期。Aronowitz［8］、Dryer［9］、Held［10］、Li［11］等对甲醇机理进行更新与完善。C0-C4核心机理研究的学者也发展并优化了甲醇的动力学模型［12-13］，使得甲醇燃烧动力学模型精度逐步提高，适用范围广，但是其规模也发展到了上百种组分和上千个基元反应，例如Burke［14］提出的Mech15.34机理包含173种组分、1 011个基元反应；Creck团队［15］开发的C3机理［16］，其包含114种组分，1 999个基元反应。对甲醇燃烧过程进行数值模拟时，需要将甲醇燃烧的动力学机理与流动方程组耦合起来进行数值求解，如果直接使用甲醇的详细燃烧动力学机理，会使计算量非常大［17］。此外，过多的组分所涉及的反应特征时间尺度差异较大。对于反应速率较快的基元反应，求解其微分方程时需要用到非常小的步长，使得微分方程难以求解，导致计算的刚性问题［18］。因此，需要对甲醇详细动力学模型进行简化。

近些年来，学者们对甲醇详细动力学模型开展了简化研究。闫妍［19］利用敏感性分析法对学者Li［11］提出的甲醇详细机理进行了简化，得到了包含16种组分，17个基元反应的甲醇简化机理，该机理能较好预测（Homogeneous Charge Compression Ignition，HCCI）发动机的燃烧特性。王刚［20］通过对甲醇氧化的主要反应路径分析，得到了包含17 种组分，40 个基元反应的甲醇简化机理，该机理更适合与CFD（Computational Fluid Dynamics）多维模型耦合计算。Lindsted［21］运用敏感性分析及试验验证法，对包含52 种组分、326 个基元反应的甲醇详细机理进行了简化，简化机理含有14个C/H/O 主反应和5个子反应，且保留了详细机理的主要特征。Jing［22］利用敏感性分析法对Zhang 机理［23］进行了简化，得到27 种组分、54个基元反应的甲醇简化机理。

然而，简化机理在规模缩小的同时，必然会带来预测性能的降低，因而有必要对简化机理进行优化［24］，即在可能复制选定的试验结果的基础上，在不确定的物理现实领域内对燃烧模型的参数值，如速率参数，热力学性质参数等进行系统调整，以达到最佳效果的方法［25］。目前，国内外针对甲醇机理的优化研究相对较少，例如Olm［26］基于全局优化算法对Li 机理［11］的17 个重要基元反应的57 个阿伦尼乌斯参数进行了优化。Magnus［27］基于智能优化工具包DAKOTA 构建了用于优化动力学参数的灵活工具箱，并利用该工具箱完成了甲醇机理点火延迟时间和层流火焰速度的优化。但是目前针对微小尺度燃烧条件下甲醇机理的优化研究还鲜见报道。为此，本文采用分级优化的方法，对基元反应速率参数的指前因子进行粗扰动调整，得出机理预测参数随指前因子的变化规律，再通过细化扰动调整，分析寻找最佳指前因子，从而最大程度的提高模型的预测性能。选择C3甲醇详细机理为研究对象，利用基于误差传递的直接关系图法（DRGEP）、全物种敏感性分析法（FSSA）和基于反应路径分析的直接关系图法（DRGPFA）分别进行了简化研究，此外还考虑到简化带来的误差，利用敏感性分析和指前因子扰动法对简化机理进行了分级优化，提高简化机理的预测精度。

1 研究方案

1.1 机理简化方案

由于C3甲醇详细机理的规模相对不大，组分和基元反应数目适中，为此，本文选择了使用较广泛的单一简化方法和组合简化方法分别对详细机理进行简化。

（1）基于误差传播的直接关系图法（DRGEP）：从误差传播的角度去分析剔除某一物质对目标物质所产生影响，若其累积误差小于设定阈值则认为该物质为冗余物质，可以从详细机理中剔除［28］。

（2）全物种敏感性分析法（FSSA）：以敏感性分析法为基础对所有目标产物进行敏感性分析，进而根据全物种敏感性系数判断出各个基元反应之间的相关性，并判断这些相关反应对所有目标物质影响程度，清除对目标产物无明显影响的基元反应，进而得到简化机理［29］。

（3）基于反应路径分析的直接关系图法（DRGEPSA）：直接关系图法中的误差仅考虑预选物质的第一代（直接关系），而通过路径通量分析，能体现第一代和第二代或更高代的重要性，通过代替使用绝对反应速率，使得生产和消耗通量都用于识别重要的反应途径，能在保持目标精度的同时尽可能生成较小的机理［30］。为此，本文采用它们的组合对机理进行简化。

基于微小尺度燃烧的特点，确定机理简化工况条件为：温度T=1 100～1 400K、当量比φ=0. 75～1. 25及压力P=1～1. 5 atm。采用Chemkin软件中的闭式均相反应器模型，在简化工况条件下对甲醇的燃烧过程进行计算，利用Reaction Workbench 软件，以点火延迟时间的最大误差作为目标参数，得到具有不同误差的简化机理。

1.2 机理优化方案

首先通过点火延迟时间和层流火焰速度的敏感性分析，筛选出关键基元反应。基于阿伦尼乌斯公式［31］，化学应速率常数的计算公式如式（1）所示：

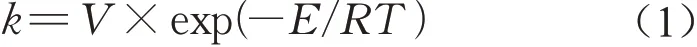
式中：k为化学应速率常数；V为指前因子；E为活化能；R为摩尔气体常数和T为温度。

指前因子V是化学反应的重要动力学参数之一，利用指前因子扰动法［32］对关键基元反应的指前因子进行修正，进而提高点火延迟时间和层流火焰速度的预测精度，达到优化的目的。优化选取的工况与简化工况一致，优化过程分为粗扰动和细化扰动，粗扰动设计方案如表1所示，细化扰动则是以最佳粗扰动为基础，根据粗扰动所得到的规律，进行局部指前因子变化量优化。

表1 粗扰动设计方案Tab.1 Coarse perturbation

1.3 机理验证方案

通过比较点火延迟时间和层流火焰速度的实验值和计算值，对机理进行验证。实验值来源于公开发表的文献中的数据，计算值是通过详细机理、简化机理、优化机理和Chemkin 软件中的闭式均相反应器模型、层流燃烧火焰模型的耦合计算得出。计算的边界条件为：当量比φ为0. 75～1. 25，压力P为1～1. 5 atm，温度T为1 100～1 400K。为了对实验值和计算值的差异进行定量分析，层流火焰速度的误差分析采用常规的误差计算式（2），点火延迟时间的误差分析采用对数相对误差式（3）。

式中：M1为层流火焰速度误差；M2为点火延迟时间误差；Me为点火延迟时间和层流火焰速度的参考值，即实验值或采用详细机理的计算值；Ms为采用简化机理和优化机理得到的点火延迟时间和层流火焰速度的计算值。

2 验证和分析

2.1 甲醇简化机理的验证和分析

表2为简化机理与详细机理规模和预测性能的对比，数据来源于Reaction Workbench 软件的计算结果。表中的最大误差为采用三种不同规模的简化机理预测的点火延迟时间与详细机理预测结果之间的误差。可以看出，三种简化机理的规模均远小于详细机理，且计算时间较详细机理大幅减少，均小于详细机理所需计算时间的1/3，DRGEP 简化机理的误差最小，但是组分和反应数相对较多，计算时间最长；FSSA 简化机理的组分与反应数最少，计算时间最短，但误差最大；DRGPFA 简化机理的组分和反应数适中，最大误差和计算时间均与FSSA 简化机理非常接近。

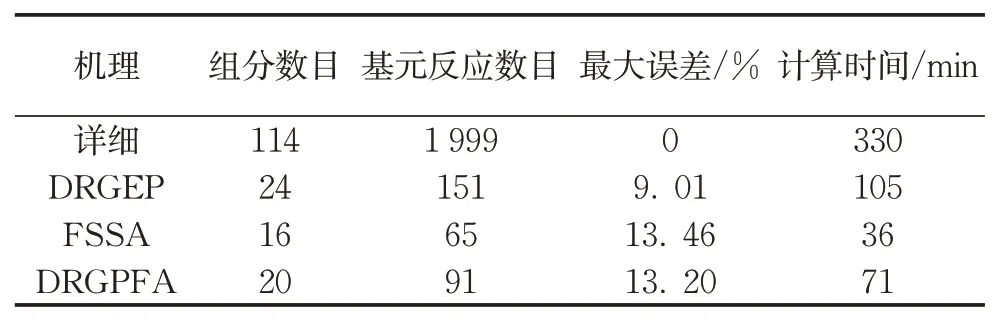
表2 简化机理与详细机理的规模和预测性能的对比Tab.2 Comparison of scale and predictive perfor⁃mance of reduced and detailed mechanisms

2.1.1 点火延迟时间

图1为温度范围为1 100～1 400 K，当量比φ=1.0，压力P=1. 5 atm下的点火延迟时间计算值与实验值，其中实验数据来自Pinzón［33］的激波管实验。由图1可知，在温度系数（1 000/温度）为0. 70～0. 83（温度值在1 200～1 400K）范围内，点火延迟时间的计算值与实验值较吻合，其中DRGEP简化的甲醇机理的计算值与详细机理计算值更接近，FSSA和DRGPFA两种简化机理的计算值接近，与详细机理计算值保持一定偏差；当温度系数为0.83～0.91（温度值在1 100K～1 200K）范围内，四种机理的点火延时时间的计算值逐渐接近，但与实验值的偏差增大，所以需要对1 100K～1 200K低温段进行优化研究。

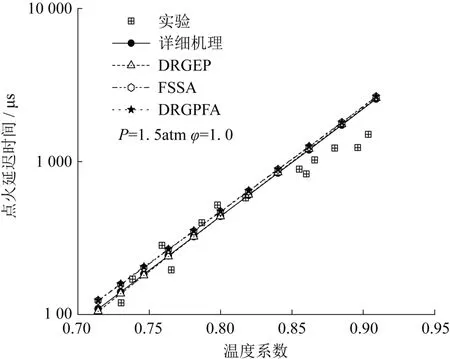
图1 点火延迟时间对比Fig.1 Comparison of ignition delay time

表3为点火延迟时间的误差分析，可见，从点火延迟时间的角度，DRGEP简化机理优于FSSA简化机理，FSSA简化机理略优于DRGPFA简化机理。

表3 点火延迟时间的误差Tab.3 Error comparison of ignition delay time

2.1.2 层流火焰速度

图2为当量比φ=0. 75～1. 25，压力P=1atm，温度T=298K下，层流火焰速度的计算值及实验值，实验数据来自Egolfopulos［34］的层流火焰实验。由图2可知，当φ＜1. 0，DRGEP简化机理计算值与详细机理的计算值曲线几乎重合，且与实验值比较吻合；当φ＞1. 0，DRGEP简化机理与详细机理的计算值偏差逐渐增大，同时和实验值偏差也增大。对于FSSA和DRGPFA两种简化机理计算值与详细机理计算值及实验值始终保持一定的差距，并且随着当量比的增加，差距越来越大，因此需要着重考虑高当量比1. 1～1. 25下的层流火焰速度优化。

图2 层流火焰速度对比Fig.2 Comparison of laminar flame speed values

表4为层流火焰速度的误差分析，从层流火焰速度的角度，DRGEP 简化机理优于DGRPFA 简化 机理，DRGPFA简化机理优于FSSA简化机理。

表4 层流火焰速度的误差Tab.4 Error of laminar flame speed

2.2 甲醇优化机理的验证与分析

根据DRGEP、FSSA 及DRGPFA 三种简化机理点火延迟时间和层流火焰速度的综合分析，DRGEP 简化机理与详细机理最接近，但是规模较大，FSSA 简化机理的组分与反应数目最少，而且误差适中，为了有利于后续与CFD 软件耦合计算，因此优先选择FSSA机理进行优化。

2.2.1 敏感性分析

（1）点火延迟时间的敏感性分析

图3为三种不同温度下，对点火延迟时间比较敏感的基元反应所对应的敏感性系数值，由图3 可知，基元反应R14 只有在温度T=1 100K 时对点火延迟时间有影响作用，R21 和R 54 对T=1 400K 时的点火延迟时间无影响。结合前文分析，主要考虑对低温范围进行优化，所以优先选择对基元反应R14、R21和R54进行点火延迟时间的修正。

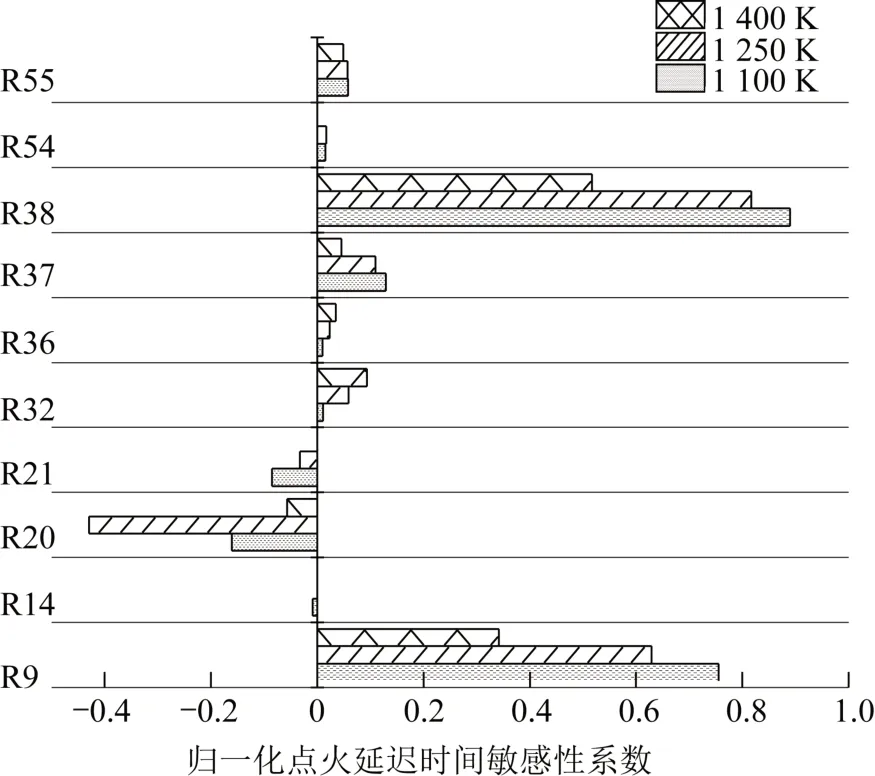
图3 点火延迟时间敏感性系数Fig.3 Normalization of sensitivity coefficient of ignition delay time

（2）层流火焰速度的敏感性分析

图4为三种不同当量比下，对层流火焰速度比较敏感的基元反应所对应的敏感性系数值，从图4中可以看出当量比在1. 0～1. 25范围内，基元反应R6和R59对层流火焰速度有影响，对低当量比0. 75无影响。结合前文分析，需要着重考虑当量比在1. 0～1. 25范围内的优化，所以针对层流火焰速度的修正，选择优化R6和R59两个基元反应。

图4 层流火焰速度敏感性系数Fig.4 Normalization of sensitivity coefficient of laminar flame speed values

（3）粗扰动待修正基元反应

结合点火延迟时间和层流火焰速度，发现基元反应R14、R21和R54对层流火焰速度无影响，R6和R59 同样不影响点火延迟时间，最终确定待修正的基元反应为R6、R14、R21、R54和R59，表5为这些基元反应的化学方程式和指前因子。

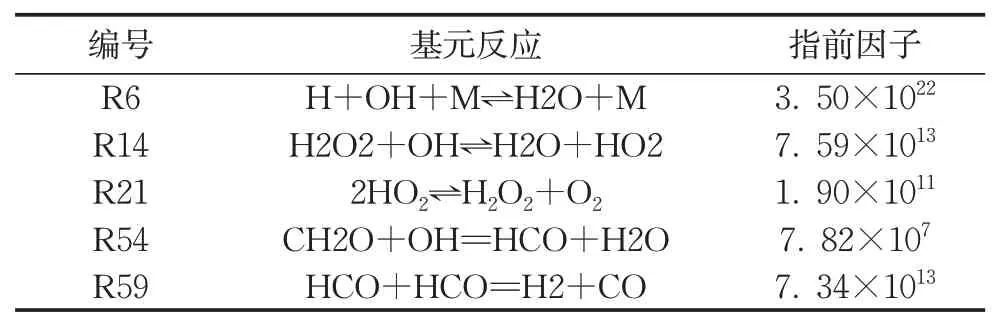
表5 待修正基元反应方程和指前因子Tab.5 Primitive reaction equation and pre-expo⁃nential factor to be modified

2.2.2 粗扰动分析

（1）点火延迟时间

图5为粗扰动下点火延迟时间的计算值，从图中可以看到V3与详细机理的偏差最大，其他优化后的机理都与详细机理的计算值较为接近，其中V6比详细机理的计算值更加接近于实验值，因此选择V6为点火延迟时间的最佳粗扰动进行下一步研究。

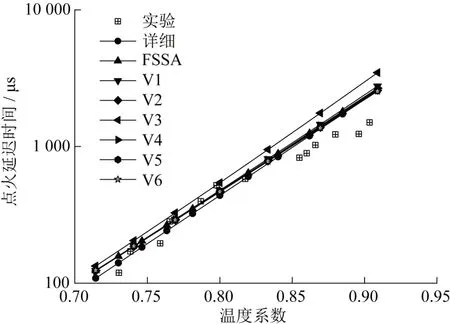
图5 粗扰动下点火延迟时间Fig.5 Ignition delay time in coarse perturbation

（2）层流火焰速度

图6为粗扰动下层流火焰速度的计算值，从图中可以看到V1～V3 的偏差过大，只有V6 接近于实验值，但是高当量比下仍有一定的偏差。因此选择V6为层流火焰速度的最佳粗扰动进行下一研究。

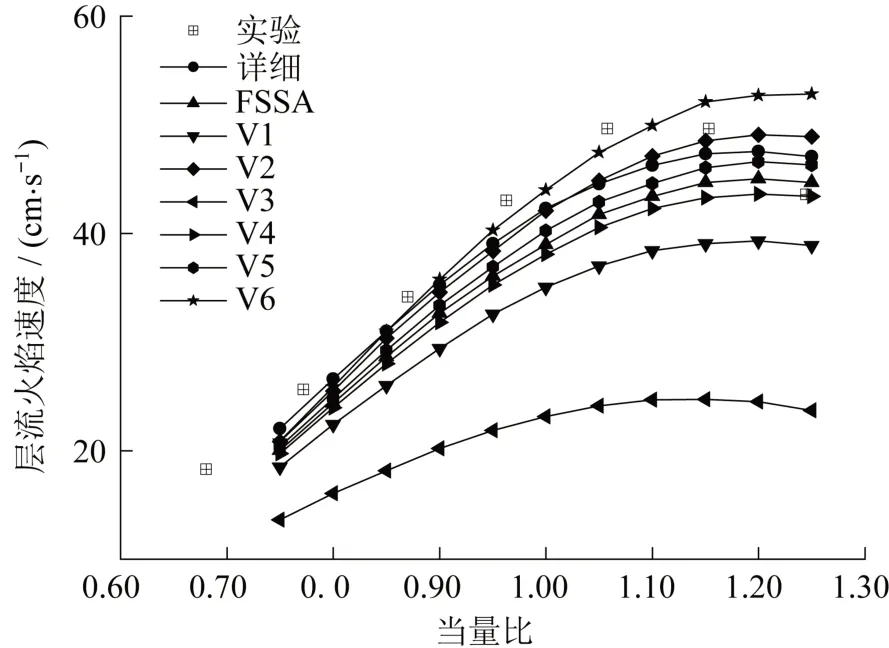
图6 粗扰动下层流火焰速度Fig.6 Laminar flame speed in coarse perturbation

2.2.3 细化扰动分析

经过粗扰动分析，确定了最佳粗扰动V6，接下来则不再对筛选出的关键基元反应进行整体修正，而是局部修正，进而使得优化机理预测的点火延迟时间与层流火焰速度更加接近于实验值。

（1）点火延迟时间

由图5可知，修正过后的机理V6预测的点火延迟时间，仍在低温下有较大偏差，高温下有较小的偏差，所以先考虑对有低温敏感而对高温敏感性不大的基元反应进行修正，由于R14 和R54 的归一化敏感性系数值太小，所以这三个基元反应只选择R21进行低温下的修正。高温下也需要略微修正，由图3可知，R32 和R37 都满足要求，R32 对高温的敏感性系数更大，对中低温不敏感，R37 则恰好相反，所以选择R37不仅可以对高温段的点火延迟时间进行略微修正，还能对中低温段起着更大幅度的修正，最终选择对R21和R37进行修正。

根据前文粗扰动研究发现，正敏感性系数能减少点火延迟时间，负敏感性系数能增大点火延迟时间，所以对于R21 应适当减小，R37 适当增大。因此，设计了表6所示的V6-1、V6-2、V6-3三种修正系数。计算结果如图7 所示，发现V6-3 的计算效果最理想，此外V6-1、V6-2和V6-3的点火延迟时间计算值的变化趋势验证了上述结论的准确性。

表6 细化扰动Tab.6 Refined perturbation

图7 细化扰动下点火延迟时间Fig.7 Ignition delay time in refined perturbation

（2）层流火焰速度

机理V6的计算值在低当量比0. 75～1. 10范围略微偏低，而在高当量比为1. 10～1. 25 范围偏高，因此需要对这两部分进行修正。对点火延迟时间修正的基元反应R21和R37对层流火焰速度几乎无影响，故在V6-3 优化的基础上，以提高层流火焰速度的预测性能为目标，对机理进一步优化。

对于低当量比下的层流火焰速度，选择R57 进行优化，因为R57 对低当量比下的层流火焰速度影响大，对中高当量比工况下影响较小；对于高当量比的层流火焰速度优化则继续选择R6 和R59。当层流火焰速度的敏感性系数为负值时，绝对值越小，层流火焰速度反而会增大，所以对于R6和R59应适当增大，R57适当减小。因此，设计了表6所示的V6-3-1、V6-3-2、V6-3-3、V6-3-4四组修正系数。计算结果如图8所示，四种优化机理的预测值与实验值相比，其中机理V6-3-4在低当量比和高当量比的计算值与实验值较为吻合，中当量比下的偏差也较小，因此V6-3-4作为最佳层流火焰速度修正系数。

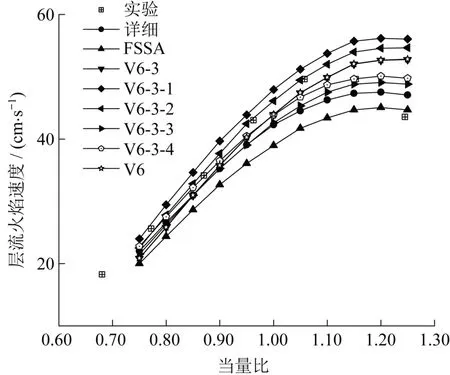
图8 细化扰动下层流火焰速度Fig.8 Laminar flame speed values in refined perturbation

表7为结合粗扰动和细化扰动下的所有修正的基元反应及修正前后的指前因子，其中由于基元反应R59 在粗扰动中缩小十倍，在细化扰动中扩大十倍，相当于没有调整，所以舍去反应R59。

表7 修正基元反应优化前后指前因子的对比Tab.7 Comparison of pre-exponential factors

2.2.4 优化机理的验证

图9为最终优化机理V6-3-4与点火优化机理V6-3的点火延迟时间计算值，二者曲线重合，这说明了本研究中点火延迟时间优化与层流火焰速度优化的相互独立性。图10为详细机理、FSSA简化机理和优化机理V6-3-4的计算值相对于实验值的平均误差，点火延迟时间的平均误差分别为：5. 22%、9. 82%和3.13%，层流火焰速度的平均误差分别为：6.35%、13.06%和2.52%。可以发现优化机理V6-3-4的预测精度相对于FSSA简化机理有了较大幅度的提升，而且相对于详细机理与实验值吻合程度更好。

图9 点火延迟时间Fig.9 Ignition delay time

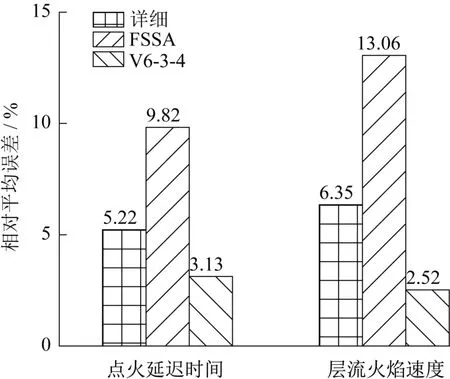
图10 计算值与实验的误差Fig.10 Error between simulation and experiment

3 结论

（1）在微小尺度燃烧工况条件下，对甲醇C3 机理详细机理进行简化，通过分析简化机理对点火延迟时间与层流火焰速度的计算性能，验证了简化机理的准确性。结果表明：与详细机理相比，DRGEP、FSSA、DRGPFA 简化机理预测点火延迟时间平均误差分别为1. 31%、7. 46%和8. 36%，预测层流火焰速度平均误差分别为3. 78%、6. 94%和4. 21%；与实验值相比，三种机理预测的点火延迟时间的平均误差分别为5. 22%、9. 82%和10. 11%，预测层流火焰速度的平均误差分别为6. 90%、8. 96%和8. 19%。包含16种组分、65个基元反应的FSSA简化机理具有较好的预测性能和较小的规模。

（2）基于点火延迟时间与层流火焰速度的敏感性分析，确定了FSSA 简化机理初步待修正基元反应：R6、R14、R21、R54 和R59；基于粗扰动、细化扰动分析，确定了最终的待修正基元反应：R6、R14、R21、R37、R54 和R57，得到了相应的修正值和优化机理V6-3-4。

（3）对比分析了详细机理、FSSA简化机理、V6-3-4优化机理对点火延迟时间、层流火焰速度的预测性能，结果表明与实验值相比，三种机理预测点火延迟时间平均误差分别为5. 22%、9. 82%和3. 13%，层流火焰速度平均误差分别为：6. 35%、13. 06%和2. 52%。V6-3-4优化机理具有良好的预测性能。

作者贡献声明：

张鹏：研究方法、数据建模和计算、论文撰写。

倪计民：研究方案、方法论指导、论文修改。

石秀勇：研究方案、数据建模指导、论文修改。