导弹发射过程同心筒内燃气流场研究*

曹 亮

（驻郑州地区军事代表室 郑州 450006）

1 引言

垂直发射的优越性在于大大节省了军舰的舰面空间，即：跟其他发射方式相比较，在甲板面积相同的情况下，垂直发射方式可装载更多数量的导弹，因而垂直发射方式广泛应用于现代化军舰上，比如俄罗斯的SA-N-6 垂直导弹发射系统，美国的MK-41 垂直发射系统，英国的“海狼”垂直导弹发射系统等等。当垂直发射导弹时，由于受导弹发射空间的局限性，发射导弹时会喷射出大量高温、高速的燃气流，所以能够可靠地、顺利地排导燃气对发射导弹来说非常重要，这直接影响到导弹发射是否成功，因此对导弹发射过程燃气流场开展研究具有重要的意义和价值［1～6］。

本文基于有限体积法，通过求解三维雷诺平均N-S 方程，建立Realizable湍流模型，并利用动网格技术来模拟导弹的运动，对导弹发射过程中导弹发射筒内燃气流场进行数值模拟，得到发射筒内不同位置温度和压力等参数值随时间的变化情况，并通过调整发射筒前盖破碎条件，分析和研究了发射筒前盖破碎对于内燃气流场的影响［7～13］。

2 理论基础

2.1 流场计算方程

本文中燃气流场采用求解非定常、雷诺平均的N-S方程的方法进行数值模拟，具体控制方程如下［7］。

质量守恒方程：

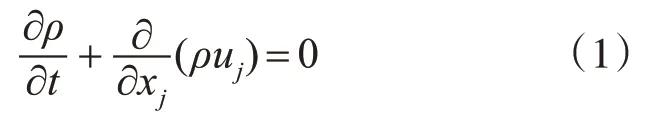
2.2 导弹运动方程

2.3 动网格技术

动网格模型通常采用定义边界或网格节点运动的方式来模拟部件的运动，这种技术最接近真实物理场景。根据其运动定义方式的不同，动网格运动分为隐式和显式运动。隐式运动可通过牛顿定律，依据部件受力情况算出其运动速度；而显式运动直接给定运动部件的运动速度。

动网格模型最核心的技术在于其部件运动导致网格运动的处理，本文采用Layering 方法，该方法非常适用于线性运动，其基本原理为通过设定压缩和分裂因子，当网格被压缩或拉伸时，超过阈值后网格即被合并或分裂。

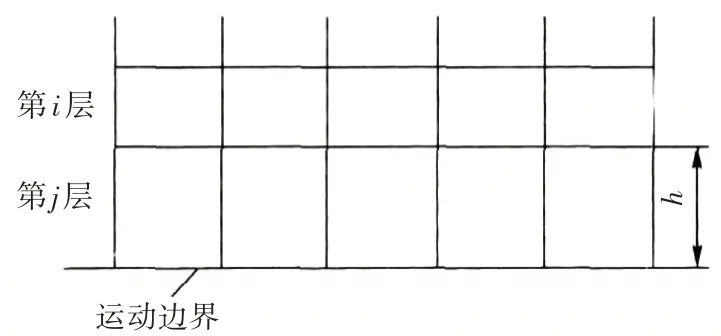
图1 Layering法原理示意图

网格的分裂与合并按以下方式进行，当网格被拉伸时，满足下式，网格分裂：

其中，h 为第j 层网格的高度，αs为网格分裂因子，hideal为理想网格高度，当上式满足时，第j 层网格分裂为两层。

当网格被压缩时，满足下式，网格被合并：

其中，αc为合并因子，当上式满足时，第i 层和第j层被合并，如图1。

3 计算模型

3.1 模型概述

固体火箭发动机燃气流是很复杂的高温高压高速流，其成分很复杂，气体固体混合并且经常伴随着复杂的化学反应。在计算中通常不考虑固体颗粒相，且燃气按性质单一、均匀混合、无化学反应、可压缩气体处理；燃气流和外界环境之间一般不发生化学反应；壁面热边界为绝热边界，忽略与外界环境之间的传热。同时不考虑导弹的尾翼和燃气舵对流场的影响。简化后的计算模型如图1所示，喷管喉部ab 设定为压力入口，处于临界状态，即Ma=1，给定总压p0、总温T0；发射箱底部、发射箱顶端cd、ef设定为压力出口，给定出口压力，如图2所示。

计算中，参考发动机试验测试数据，入口总温为气体的定压燃烧温度，总压为发动机燃烧室压强。

图2 计算模型示意图

3.2 计算模型和网格

燃气流场数值模拟的模型网格数为120 万个，为非结构化网格，如图3 所示。在计算中，设定时间步长为0.01ms，计算时间为1.5s，本文参考某型发动机试验测试数据，入口总温为气体的定压燃烧温度3000K，总压为发动机燃烧室压强10MPa，理论上取无穷远处大气环境状态作为燃气流出口状态，在计算中采用扩展边界，让计算区域足够大，使其满足出口压强为环境压强，即 pout=p∞（1 个大气压），计算区域内初始压强、温度和速度为周围环境条件（分别设定压强为1013.25Pa，温度为300K，速度为0m∕s），发射筒前盖采用燃气胀破式，通过查阅有关文献，破裂压强分别取值0.03MPa和0.05MPa。

图3 数值计算模型

4 数值计算结果与分析

试验中，测点分别设置在发射筒的前部、中部和后部，发动机点火后，燃气压力波作用在发射筒底部导流尾盖，被导流尾盖导向发射筒内外筒之间的燃气排导通道。燃气压力波在内外筒之间的通道向发射筒盖运动，作用在筒盖上，当压力达到设定值，筒盖破裂。

从图4 可以看出，导弹发射过程中，发动机燃烧室内压力最大，压力从燃烧室进入发射筒的过程中，压力逐渐降低，并且内外筒之间的通道内的压强明显大于内筒内的压强。

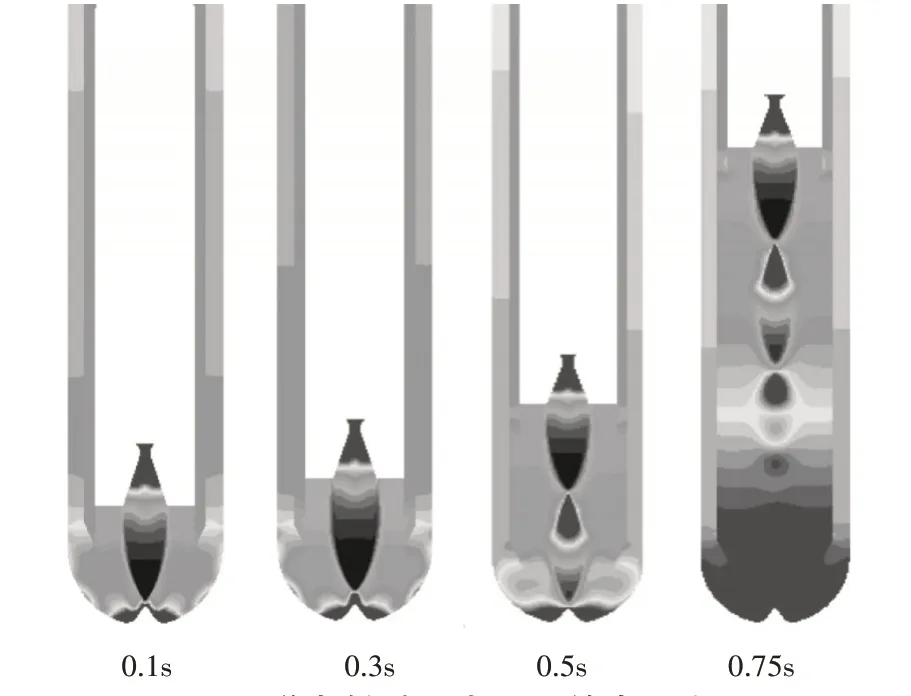
图4 导弹发射过程中同心筒内压力云图

燃气从发动机喷出之前，首先在扩张管里迅速加速膨胀，随着其射流速度的增加，周围的空气不断被压缩、叠加，从而产生正冲波。然后，冷空气被迫向下运动，直到被压缩到导流板上，速度相应降低，导流板上将出现一高压区，使一部分燃气流反冲进入发射筒内，进而使导弹处于高温状态。随后，燃气流开始向侧面和向上运动，逐渐形成正冲区，导致发射筒内压强被迫升高，燃气流的两条斜拦截激波开始收缩并交叉，此时正冲波消失，燃气流的激波结构开始交替出现压缩波节与膨胀波节的现象。

图5 导弹发射过程中同心筒内速度云图

图5 给出了发射箱内速度分布，从中可以看出燃气流经过喷管，速度逐渐增加，但仍处于欠膨胀状态。经过喷管后，在第1 个波节内沿轴线方向速度继续增加，经斜激波后速度下降；第2 个波节内的参数变化趋势与第1 个波节相同，变化幅度减小，且内外筒之间通道内燃气的速度大于导弹和内筒壁间燃气的流速。

观察图6 发现，发射筒发射导弹时，高温燃气在经过喉部后，由于速度不断提高，温度也随之下降，在激波前，温度较低，激波后温度陡增。

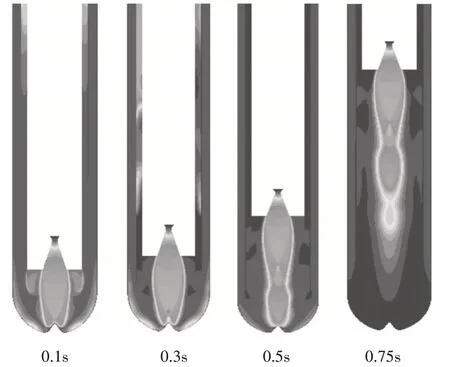
图6 导弹发射过程中同心筒内温度云图

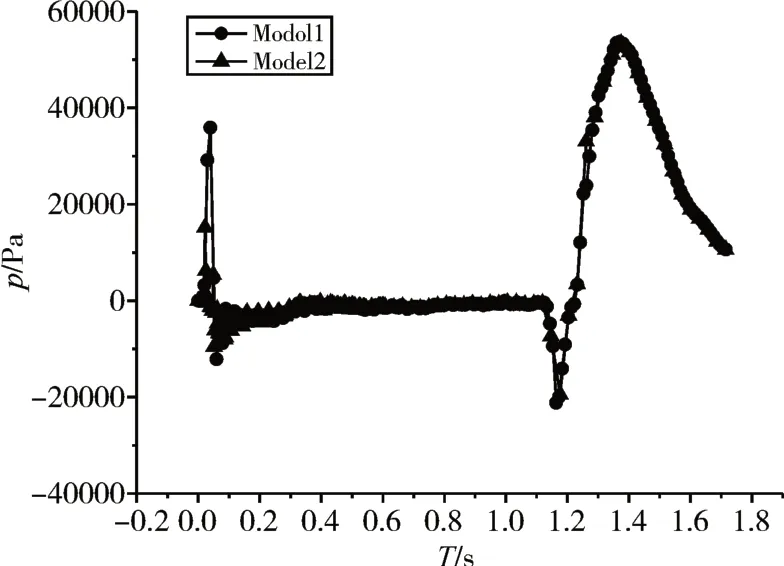
图7 导弹发射过程中同心筒前部测点压强时域曲线

图7 是导弹发射过程中发射筒前部压强（压力）时域曲线，其中Model1 显示的是前盖在0.05MPa 压强下破碎时的数值模拟结果，Model2 显示的是前盖在0.03MPa 压强下破碎时的数值模拟结果，从图中我们可以看出，在发动机点火后大致0.1s 的时间内，压力曲线急剧上升，出现了一个明显的峰值，随后压力又急剧变小，甚至一小段时间出现了负值，这是因为在点火后的短时间内，发射筒前盖完好，它是一个密闭的空间，从发动机喷出的大量高温高压燃气流，经过内筒和外筒之间的间隙，迅速到达发射筒前盖附近，使得前盖附近的压强急剧增大，当压强达到前盖的破碎压强时，前盖破碎，使得压强迅速减小。在0.1s～1.1s 时间内，是筒盖破碎和导弹向上运动的过程，前部压强基本保持恒定，变化很小；在1.1s～1.2s时间内，压强快速减小后，又迅速上升，1.2s～1.8s压强急剧变大，达到峰值后，开始相对缓慢的下降。

如图8 所示，与导弹发射过程中发射筒前部测点压强时域曲线相比，中部测点和后部测点的压强时域曲线在峰值段出现的时间有很大的差别，前部测点压强时域曲线在大约1.4s时达到峰值，中部测点压强时域曲线在大约1.2s时达到峰值，后部测点压强时域曲线在大约0.9s时达到峰值，这种差别是因为导弹向上运动的过程中，发动机跟随弹体先经过发射筒后部测点后经过发射筒前部测点。

图8 导弹发射过程中同心筒中部测点压强时域曲线

如图9 所示，通过对比前部、中部和后部时域曲线中的Model1 和Model2，我们发现在0～0.1s 时间段，Model1 的压强峰值明显大于Model2 的压强峰值，Model1 采用的前盖破碎条件是压强达到0.05MPa，Model2 采用的前盖破碎条件是压强达到0.03MPa，因此通过调整前盖的破碎条件，可以减小燃气流对发射筒的冲击。

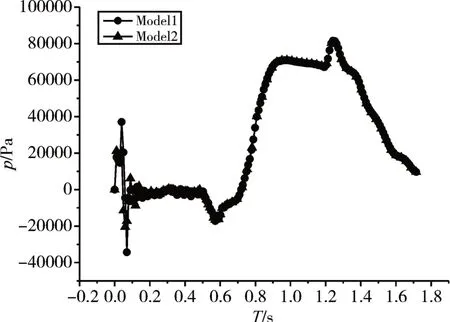
图9 导弹发射过程中同心筒后部测点压强时域曲线

5 结语

本文通过采用数值模拟方法，建立模型，研究了发射筒内不同位置温度、压力等参数随时间的变化情况，对导弹发射过程中发射筒内燃气流场进行了分析研究，得到以下结论。

1）在导弹正常发射过程中，发射筒内的压强会出现两个峰值，一个是出现在发射筒前盖破碎前，这个峰值大约出现在点火后的0.1s内；第二个峰值出现在发动机随弹体向上运动的过程中，发射筒的后部先出现峰值，出现时间大约为0.9s，前部最晚出现峰值时间大约为1.4s。

2）通过调整发射筒筒盖的破碎压强，可以明显改变发射筒内第一个峰值的大小，从而为导弹发射筒的优化设计和改进研制提供借鉴和参考。