山区高速公路限速控制与路线指标的相关性分析

张 邹，郭 鑫

(广西交通设计集团有限公司，广西 南宁 530029)

0 引言

超速行驶一直是致命性交通事故的主要原因之一。现阶段交通建设任务重心正逐步转向西部山区，区别于繁华地段，山区高速公路车流量小，驾驶人不会因拥堵主动降低行驶速度，更有可能超速并造成交通事故。另外，研究表明，道路属性是驾驶人选择车速的主要依据。通常来说，较为平缓或简单的线形组合能够缓解驾驶员的焦虑情绪。相反，复杂且多变的地形地貌往往导致其道路属性同样复杂，驾驶人选择车速变得更加困难。因此，有必要对山区高速公路进行速度控制，以期增加交通运行的安全性。

本文论述了限速控制计算与路线设计之间的相互作用，分析了线形指标在限速计算中的应用情况，以及两种设计速度(几何容许速度与设计速度)对道路路线设计的影响，对未来的道路设计提供相应参考，同时期望降低桥隧等在山区高速公路中的比例，减少“高填深挖”，进而降低建设成本。

1 基于路线复杂性的风险分析

山区高速公路的路线设计是研究重点亦是难点。为了在不超出施工成本的前提下，尽可能保障交通安全，在道路设计中应尽量采用较高的设计指标。然而，山区地形地貌的固有缺陷无疑会增加设计难度，从而增加了道路风险，一般采取的手段是限速控制。因此，在进行两者关系的论证之前，有必要对山区道路线形设计的难点进行讨论。

1.1 设计标准特殊性

(1)应根据远景交通量，结合地形条件，选取适宜的平纵线形指标，同时应考虑环境保护等方面因素，不宜强求公路等级上限[1]。

(2)在充分利用地形条件的基础上，应深度调查交通量组成与气候条件等因素，对线形进行排查与二次优化。

(3)在较长的山岭重丘地段，为降低对原始地貌的破坏与建设成本，应采用对应的高速公路山岭重丘区域线形指标，同时也应兼顾衔接段平纵指标的合理过渡。

1.2 平曲线特殊性

平曲线设计为路线设计工作中最重要的部分之一，该部分设计应该在保证行车安全的前提下，充分考虑舒适性与顺畅性[2]。

(1)圆曲线半径。圆曲线半径的选取是山区高速公路设计工作中的重中之重。为满足驾驶人行驶需求和高速公路服役要求，圆曲线需要绕避病害严重地段，不仅能够减小工程规模，降低工程造价，还有利于交通运行安全。

(2)最小直线长度。对最小直线长度的规定是为了避免断背曲线的出现。考虑到驾驶人操作习惯和反应速度，规定同向曲线间的最小直线长度为6V，反向曲线间的最小直线长度为2V。运行速度的分布曲线呈现正态分布，如图1所示。然而在山区高速公路的设计中，考虑到工程造价和绿色环保等要求，可以不用过分强调直线长度[1]。

图1 运行车速分布曲线图

(3)缓和曲线。在地形复杂多变的山区，缓和曲线的选取十分重要，主要表现在弯道的自然过渡、合理且高效地引导司机视线、弥补曲线间最小夹直线长度、贴合地形地貌从而克服地形障碍等方面。

1.3 纵曲线特殊性

与平曲线设计相似，山区高速公路纵断面设计对线形指标、行车舒适性与安全性以及建设成本等均有重要影响。

(1)纵坡值的选取。在进行山区高速公路纵断面设计时，应结合交通组成、沿线地形地质和气象水文等因素综合确定最大、最小纵坡，以及是否需要设置缓和坡段，最大限度保证道路运行质量与安全。作为重要指标之一，最大纵坡的选取将直接影响山区高速公路的工程规模以及最终的安全等级评估。

(2)坡长与纵曲线半径。在我国现行规范中，根据纵面起伏的幅度大小、设置纵曲线的必要性以及行驶安全性，分别对纵断面的最小坡长和较陡纵坡的最大坡长进行了限制。根据以往的工程经验，山区高速公路采用台阶坡的形式来满足规范中的相关要求。

在山区高速公路实际运行过程中，由于山岭地形变化莫测、植被茂密，纵曲线容易出现断背曲线，影响交通运行安全。一般来讲，增大纵曲线半径可以有效提高纵断面指标，但会大大增加建设成本。因此，在进行山区高速公路纵曲线设计时应综合考虑多方面因素，选取适宜的指标。

2 基于风险的限速必要性分析

在正式论证两者之间的关系之前，应对限速的原因与原理进行说明。道路开通运行后，考虑到车辆行驶安全以及运行效率，需要通过统计与计算确定该路段的最高以及最低运行速度。其中，最高限速的设置主要是为了提高道路运行过程中的安全系数。同时，结合最低限速，可有效限制在同一时间行驶在同一道路上车辆的速度差，保障道路运行安全。此外，最低限速也是在保证安全的基础上，提高道路运行效率的有效措施。因此，公路运行中的事故率与限速有着紧密联系。

2.1 速度风险

根据物理基本原理，交通事故与速度有着密切的关系，速度增加会导致交通事故率的增大，同时加剧事故损坏程度。1981年，Nilsson提出了速度与交通事故之间的关系，如表1所示。由表1可知，当平均速度增加5%，与伤害相关的事故数量会增加约10%，同时与死亡相关的事故数量会增加约20%。通过表1中式(1)～(6)可以看出，事故数量和伤亡人数随着速度增加呈指数增长，因而对于山区高速公路进行速度限制是很有必要的。

2.2 速度差异性风险

大量的科学研究与报告表明事故发生率与速度的统计结果有关，或者说与速度的离散性或者彼此之间的差异性相关。Solomon与Cirillo’s的研究均表明速度与事故发生率之间存在U形曲线关系，如图2所示。Lave于1985年证明了死亡事故发生率(Z1)会随着速度差的增加而增加，这也初步证实了速度离散性对道路安全系数的影响。同时，哈尔滨工业大学裴玉龙[3]通过统计分析证明了亿车公里事故率(AR)与速度标准差(σ)存在指数关系：AR=9.853e0.055σ。

表1 速度与交通事故关系表

事实上，无论是速度与事故发生率，还是速度差异性与事故率的关系分析结果，都证明了速度及其统计学规律均直接或间接地影响了年均交通事故数量与事故伤亡人数。因此，山区高速公路限速是必要的。

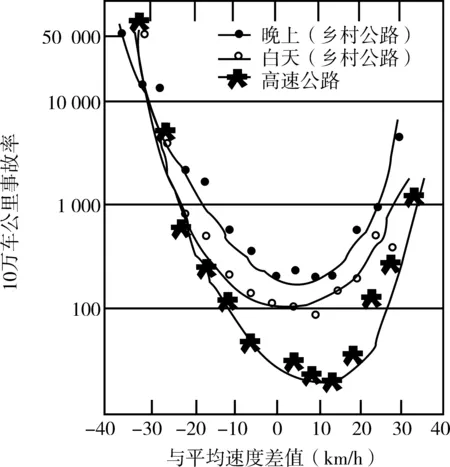
图2 速度与事故发生率之间的U形关系曲线图[4]

3 限速与路线关系论证

从前面的论证可以看出，山区高速公路的道路属性是影响交通安全的最主要因素，而限速又是保证安全的最有力手段，因而十分有必要基于山区高速公路建设对限速策略与路线设计之间的关系进行进一步讨论。

3.1 速度控制与路线设计流程

(1)几何容许速度。几何容许速度是指在理想条件(包括道路条件与其余外部条件)下，车辆能够平稳通过的最大车速。因而，在整个设计、运行、养护过程中，几何线形单元的技术指标通常会超过基于设计速度的计算值，因此，路线设计时应考虑整个过程中体系能够承载的最大车速。

(2)路线设计流程分析。道路线形设计过程如图3所示，整个过程可以分为初步设计和施工图设计两个阶段。初步设计阶段是从确定设计速度开始的，以设计速度和山区的地理地质条件为基础条件，确定基本的路线方案和几何线形，接着根据路线方案的冗余量和协调性确定限制速度，对各项技术指标进行调整，即进入施工图设计阶段。在施工图设计阶段结合几何容许速度进一步调整与优化道路几何线形方案，并最终确定道路设计方案。

图3 道路线形设计流程图

设计过程中，无论是设计速度还是限制速度，均和道路几何线形密不可分，受其影响并反作用于最终的路线方案。设计速度、路线几何线形和限制速度之间是相辅相成、相互影响、彼此为条件和结果的关系[5]。也正如图3中给出的，在调整技术指标时，既要考虑设计速度，同时也要考虑几何容许速度。几何容许速度仅依赖于几何线形指标与车辆运动受力分析，也因此和设计速度一起成为路线指标与限制速度之间相互作用的桥梁。

可见，初步设计路线方案后，考虑设计速度与几何容许速度，确定限速方案，而之后的路线设计优化过程也是以限速方案、设计速度、几何容许速度三者为基础进行的。需进一步深入理论层面，剖析线形指标与限速控制两者之间更为具体的关系。

3.2 可能限速值与道路线形

3.2.1 可能限速值

可能限速值的影响因素有很多，其中包括上文介绍的事故死亡率与速度差，以及旅途时间和期望速度。其中期望速度与可能限速值成正相关，可以用来定量地表示限速值。旅客在途时间可以用式(7)表示：

(7)

式中：T——旅客在途时间(s)；

L——路段长度(km)；

V——运行速度(km/h)。

一般来说，限速值Vk与期望速度VE之间的关系可以由式(8)给出：

ΔVEK=VE-VK≤0

(8)

期望速度是基于心理学与动力学原理，车辆在固定道路以及其他外部条件影响下最适宜的驾驶速度。从式(8)可知，限速值与期望速度之间的差值越小越好。

3.2.2 期望速度与线形指标

效仿几何容许速度，本节拟以期望速度为跳板，建立山区高速公路限速方案与线形指标之间的联系。

道路线形对驾驶员期望速度有较大影响，不同的路线组合形式对驾驶员的心理与生理造成不同的影响，影响程度通常用驾驶员的心率增长大小表征[6]。通过研究不难得出，较为平缓的直线路段对驾驶员心理压力较小，心率增长较小；相对的，曲线起伏较大的上下坡与起伏坡段造成的心理压力较大，心率增长较大。不同地段心率增长的计算模型为：

(9)

式中：N——驾驶员心率增量(次/min)；

R——圆曲线半径(m)；

i——纵坡(%)；

W——坡度半径比，W=i/R。

利用以上心率增长模型对道路线形与限制速度进行修正，可以获得不同坡段的期望速度。

4 不同路段限速计算

4.1 驾驶人期望速度模型

基于上文分析，本节对不同道路组合形式的期望速度模型进行推导。

4.1.1 圆曲线段

利用式(9)可得期望速度下的圆曲线半径修正临界值457 m与491 m，从而可以得到小车和大车的期望速度为：

(10)

(11)

4.1.2 纵坡段

根据式(9)，由于大车驾驶员期望速度修正临界值(iXC=3%)的限制，本研究认为该种组合形式不会对驾驶员对速度的心理预期造成影响。因此无须计算，直接取用初始值(120 km/h和85 km/h)即可。

4.1.3 弯坡组合段

根据式(9)可得小车、大车的期望速度修正值分别为0.03和0.008，从而得到小车和大车期望速度关系值：

(12)

(13)

4.2 实例分析

考虑到山区高速公路的特殊性，本节以西部山区某高速公路为例，基于其部分路段的线形数据，将路段分为平曲线段、纵坡段和弯坡组合段，分别代入上式计算出期望速度，和实测速度进行对比，如表2所示。

表2 不同设计指标限速结果表

从限速结果来看，线形指标以及线形组合确实与山区高速公路的限速控制相互影响，且这种影响可以通过期望速度的计算过程定量表示出来。分析结果如下：

(1)在三种线形组合中，平曲线半径对平曲线线形下道路的期望速度计算影响最大，计算结果随着半径的增大而增大。

(2)坡度的变化造成坡度半径比W变化，从而影响到平纵组合段的期望速度值，但这一影响仅在W超过一定值时出现。

(3)平曲线段、纵坡段及弯坡组合段计算得到的期望速度值有所差异，对比实际的限速参考值，以道路线形指标为影响因素计算的驾驶员期望速度能够给最终的限速控制方案提供参考。

5 结语

本文从山区高速公路路线的复杂性与设计难点出发，解释了此类地区交通事故高发的原因，并利用风险评估剖析了限速控制的原因与重要性。最后，利用期望速度与限速值的正相关性，定量分析了道路路线指标与组合形式对限速计算的作用。研究表明，山区高速公路的路线指标是运行过程中限速控制的重要基本依据，而限速控制也会在设计过程中影响线形指标的调整。