基于有效角动量函数的多参数极移预报*
赵 鑫 吴元伟 杨新宇 杨旭海 张首刚
(1中国科学院国家授时中心 西安 710600)
(2中国科学院大学电子电气与通信工程学院 北京 100049)
(3中国科学院精密导航定位与定时技术重点实验室 西安 710600)
(4中国科学院时间频率基准重点实验室 西安 710600)
1 引言
地球在空间中的受力非常复杂,外部受到太阳、月球及行星的万有引力作用,内部受到大气、海洋、地壳、地幔等圈层相互作用的影响[1],导致了地球的自转不恒定.一方面,自转速率随着时间变化;另一方面,自转轴的方位也随着时间变化.通常,地球的方位可以用地球定向参数(Earth Orientation Parameters,EOP)来描述,包括章动参数、世界时(Universal Time,UT1)和极移参数(Polar Motion,PM),其中,极移参数包括极移X和极移Y两个分量,这些参数与国际天球参考架(International Celestial Reference Frame,ICRF)和国际地球参考架(International Terrestrial Reference Frame,ITRF)之间的转换密切相关[2].地球定向参数对于许多科学研究和工程应用具有重要的作用,例如,在大地测量学、天文学、航海以及时间保持等领域,不仅需要实时地球定向参数,也需要高精度的地球定向参数预报[3].国际地球自转服务(International Earth Rotation Service,IERS)定期提供并维护地球定向参数的事后产品、快速产品和预报产品.
极移是地球自转轴相对于地球表面的运动.作为地球定向参数的组成部分,极移的预报同样对于科学研究和工程应用具有重要的意义[4].近些年来,很多学者参与了极移预报的研究,并提出了多种极移预报的方法.在这些预报方法中,绝大部分都是对事后极移数据的统计外推[5],其中,最小二乘与自回归组合(Least-Squares Extrapolation and Autoregressive Modeling,LS+AR)的方法很早就被应用于极移的预报[6];于2005-2008年举行的地球定向参数预报比赛(EOP Prediction Comparison Campaign)对极移预报方法的总结以及预报精度的提升具有里程碑的意义,除了最小二乘与自回归组合的预报方法之外,其他预报方法包括:卡尔曼滤波[7]、自协方差预报[8]、模糊推理系统预报[9]、离散小波变换与自协方差的组合预报[10]以及人工神经网络等[11].极移与地球各个圈层之间的质量重分布和相对运动有着紧密的联系[12].大气角动量(Atmospheric Angular Momentum,AAM)的变化[13-14]、海洋角动量(Oceanic Angular Momentum,OAM)的变化[15-16]、陆地水圈角动量(Hydrospheric Angular Momentum,HAM)的变化以及海平面角动量(Sea-Level Angular Momentum,SLAM)的变化对于极移有着不同程度的影响[17-18].由于传统的统计预报方法没有考虑地球流体的高频质量变化导致的随机项,Dill等[19]在极移的短期预报中融合了有效角动量函数(Effective Angular Momentum Functions,EAM),从而显著提高了极移短期预报的精度;最近,Dill等[20]在极移预报中组合了大气、海洋和陆地水圈的有效角动量函数,并联合最小二乘与自回归方法,进一步提高了极移90 d内的预报精度.本文以Dill等[20]的预报方法为基础,通过使用分段最小二乘和改进的自回归模型,实现了极移更高精度的预报.
本文通过联合有效角动量函数与LS+AR的数据外推方法,分别对短期(未来1-6 d)和中长期(未来7-90 d)极移进行了预报.其中,短期极移预报外推了大地测量学的角动量(Geodetic Angular Momentum,GAM)和EAM之间的残差,并利用了EAM数据模型1-6 d的预报优势;中长期的极移预报直接外推了完整EAM(full EAM,GAM和短期预报中得到的有效角动量之间的拼接);在两个预报阶段中,使用描述地球旋转变化的刘维尔方程(Liouville Equation)实现了有效角动量和极移之间的转换.在第2节中,阐述了本文所采用的极移预报方法,对LS+AR方法的应用进行了适当的优化,一方面,采用了分段最小二乘以更好地拟合及外推EAM数据;另一方面,对于自回归参数进行了广泛的测试和搜索,选取了一组能够适应不同预报阶段的优化参数,实现了极移的多参数并行预报.本文第3节展示了多次预报实验的结果,在2019年9月至2021年2月的范围内进行了441次极移预报,并将预报结果分别与EOP 14 C04(IAU2000A)(下文简称EOP C04)和IERS Bulletin A(Bulletin A)进行了比较,完成了预报结果的评估.第4节对全文进行了总结和展望.
2 方法与数据
2.1 有效角动量及刘维尔方程
1-6 d的短期极移预报利用了EAM的预报值,并且对GAM和EAM之间的残差(GAMresidual,大地测量学的有效角动量残差)进行了外推.本文所采用的有效角动量函数EAM包括以下几个部分:AAM、OAM、HAM以及SLAM;EAM数据来源于德国地学研究中心地球系统模型组(Earth System Modelling group at Deutsches GeoForschungsZentrum,ESMGFZ)维护的ESMGFZ产品网站http://rz-vm115.gfz-potsdam.de:8080/repositor y.求解GAM residual是短期极移预报中的关键步骤,为此,需要首先获得GAM,刘维尔方程示意极移和角动量函数之间的微分关系[1],如下所示:
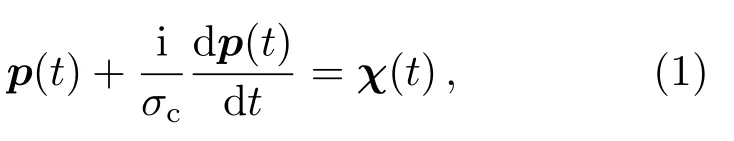
其中,t为时间变量,极移的表达式为p(t)=pX(t)-ipY(t),极移的X分量为pX(t),极移X正变化量的方向指向本初子午线;极移的Y分量为pY(t),极移Y正变化量的方向指向西经90°W.有效角动量函数的表达式为χ(t)=χX(t)+iχY(t),χX(t)和χY(t)分别是有效角动量函数的X分量和Y分量,χX(t)正变化量的方向指向本初子午线,χY(t)正变化量的方向指向东经90°E.可见,极移p(t)中Y分量pY(t)前的负号表达了极移与有效角动量函数之间正变化量方向的不一致性.σc表示钱德勒复频率[21],并且σc=2π[1+i/(2Q)]/Tcw,本文中,钱德勒摆动周期的取值为Tcw=433 d,阻尼因子取值为Q=170[22-24].
Wilson进一步推导出了下面的刘维尔方程的离散形式[25]:


以上两式中,Δt为时间增量.
由于极移数据和角动量数据的产品是离散的时间序列,因此,通过离散化的刘维尔方程即可实现极移和有效角动量之间的转换,于是GAM可以从极移数据中转换得到.本文所使用的极移数据来自IERS提供的事后产品EOP C04,快速产品以及预报产品Bulletin A,详见网站:https://www.iers.org/IERS/EN/DataProducts/data.html.
通过上文中有效角动量函数与极移之间的转换原理和相应的数据集,可以得到最近4 yr的GAM数据和EAM数据如图1所示.GAM由EOP C04的极移数据通过刘维尔方程得出.由图可知,GAM residual表现较为稳定.

图1 上面两幅子图表示GAM数据和EAM数据,其中,黑色实线为GAM,黑色点线为EAM;下面两幅子图表示GAM和EAM之间的残差;左图表示X分量,右图表示Y分量.此外,EAM=AAM+OAM+HAM+SLAM,GAM和EAM都是无量纲的.Fig.1 The top two sub-figures represent GAM data and EAM data,in which the black solid line is GAM,and the black dotted line is EAM;the bottom two sub-figures represent the GAM residual;the left figure represents the X component,and the right figure represents the Y component.In addition,EAM=AAM+OAM+HAM+SLAM,GAM and EAM are dimensionless.
此外,EAM的分量AAM、OAM、HAM、SLAM的数据特征如表1所示,可见各个分量数据的量级在10-9-10-7之间.
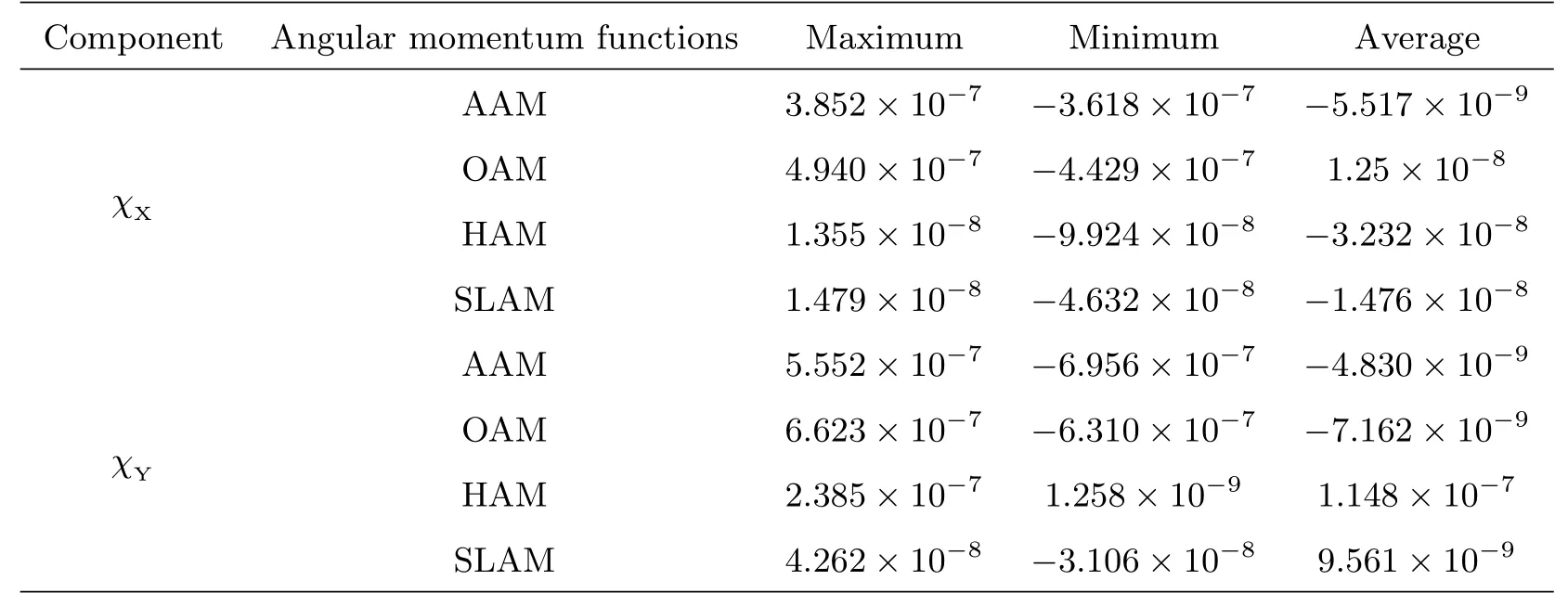
表1 2016—2021年EAM各分量的数据特征Table 1 Data characteristics of each component of the EAM from 2016 to 2021
2.2 最小二乘与自回归组合方法
在极移的短期预报和中长期预报的数据外推阶段,皆使用了最小二乘和自回归组合的方法LS+AR.为了更加准确地拟合极移短期预报中的GAM residual数据以及极移中长期预报中的GAM数据,本文在拟合数据时采用了分段最小二乘的方法.最小二乘拟合公式包括线性项和周期项,对于不同的数据段采用了不同的线性拟合公式,如下所示:
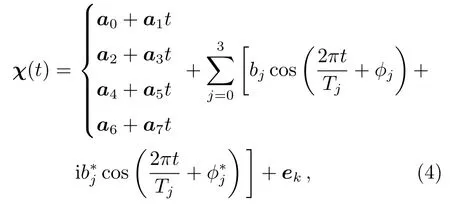
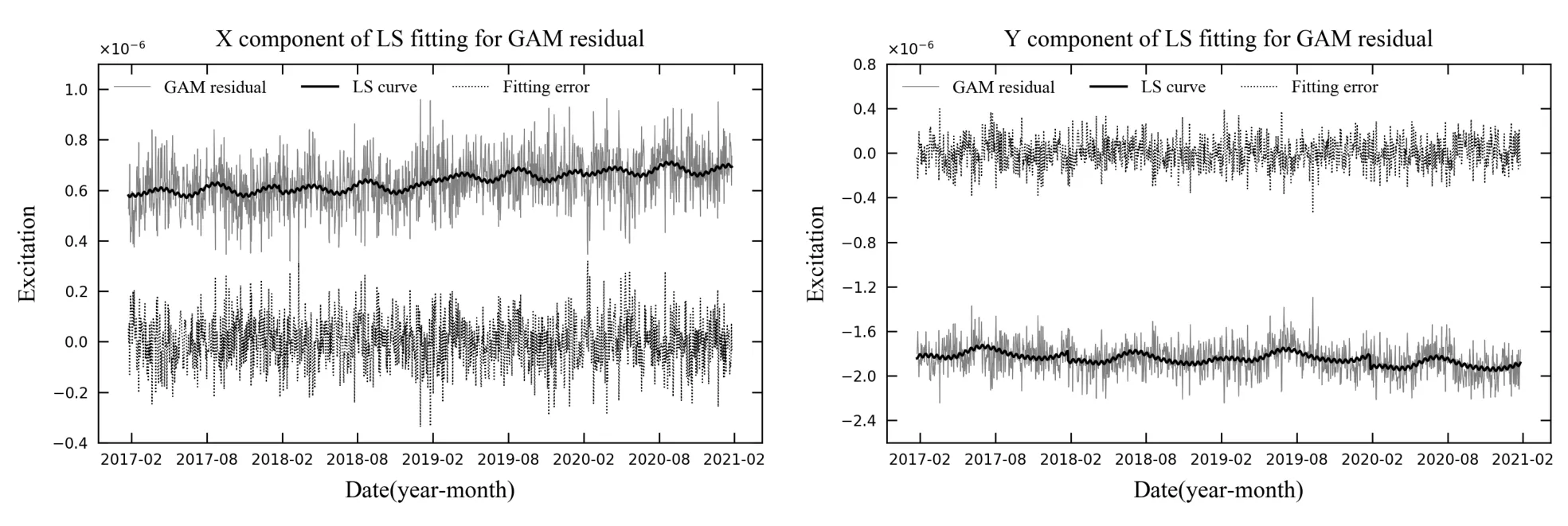
图2 灰色实线为GAM residual,黑色实线为LS拟合曲线,黑色点线为LS拟合误差;左图是X分量,右图是Y分量.Fig.2 The gray solid line represents the GAM residual,the black solid line is LS fitting curve,and the black dotted line is LS fitting error;the left picture is the X component,and the right picture is the Y component.
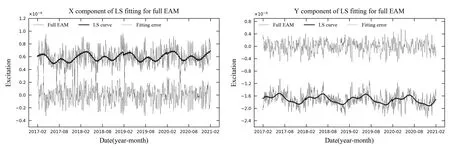
图3 灰色实线为full EAM,黑色实线为LS拟合曲线,黑色点线为LS拟合误差;左图是X分量,右图是Y分量.Fig.3 The gray solid line represents the full EAM,the black solid line is LS fitting curve,and the black dotted line is LS fitting error;the left picture is the X component,and the right picture is the Y component.
由图2-3可见,在使用分段最小二乘的方法对GAM residual以及full EAM进行拟合时,两个阶段都产生了较为平稳的拟合误差.实际上,这些最小二乘拟合误差接近于随机噪声,但由于其量级与拟合数据集(GAMresidual或者full EAM)相当,因此,最小二乘拟合误差的外推就显得尤为重要,对于GAM residual和full EAM的外推有着显著的影响.为了得到更好的最小二乘拟合误差的外推值,本文在使用自回归处理拟合误差的基础上,对于拟合误差数据进行了选择性过滤,也就是从拟合误差数据序列中间隔选取数据,之后再进行自回归操作,此方法实现了在数据选择的同时保证了数据信息的完整度,具体方法如下所述:
在外推最小二乘拟合误差时,本文使用了自回归方法,并且对最小二乘拟合误差时间序列进行了滤波,使得在不同的极移预报阶段以及不同分量的极移预报中,自回归模型能够间隔选取时间序列,以便于在更大范围的参数空间中为不同的极移预报阶段和不同分量的极移预报选择更优的参数,从而获得更优的预报结果.将实现时间序列滤波的参数称为间隔数.因此,在如下式所示的自回归模型中,可调节参数有阶数和间隔数两个,模型如下所示:
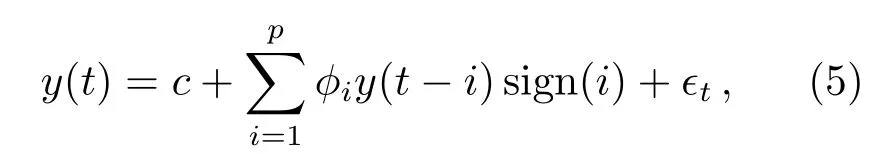
其中,sign(i)是符号函数:

y(t)表示单变量时序数据,c是自回归模型的常数项,p是自回归阶数,i表示数据的序号,φi是自回归系数,ϵt为白噪声;lag是自回归间隔数,取值范围是正整数.sign(i)是与间隔数lag有关的符号函数,实现了在求解自回归模型时,可以在阶数p的范围内以lag为间隔选取时间序列,相当于对时间序列进行了滤波.自回归模型的阶数p和间隔数lag是本文极移预报中的重要参数,下文中将详细论述.
2.3 极移预报流程
本文中,极移的预报总体上可以分为两个阶段,一是1-6 d的短期预报;二是7-90 d的中长期预报.短期预报利用了EAM数据1-6 d的预报值,首先,刘维尔方程将极移数据转换成GAM数据,与EAM数据做差,得到GAM residual.然后,通过LS+AR的方法将GAM residual外推至未来第6 d,EAM数据6 d的预报值与GAM residual数据6 d的外推值相加,获得了未来6 d的有效角动量预报值,再次利用刘维尔方程,即可将有效角动量预报值转换为极移的预报.中长期极移预报的关键在于外推GAM数据,将短期预报中得到的未来6 d的有效角动量预报值与GAM数据的历史值拼接起来,形成full EAM,利用LS+AR的方法对full EAM外推至未来第90 d,并通过刘维尔方程的转换得到7-90 d的极移预报.在极移的整个预报过程中,极移p(t)和有效角动量χ(t)以复数的形式作为整体参与计算.在Dill等人研究的基础上[20],经过多次实验测试,在短期预报中,最小二乘线性项的拟合数据段长度选取为1 yr,周期项的拟合数据段长度选取为4 yr,自回归模型的拟合数据段长度选取为4 yr;在中长期预报中,最小二乘线性项的拟合数据段长度选取为1 yr,周期项的拟合数据段长度选取为4 yr,自回归模型的拟合数据段长度选取为1 yr.
3 结果与讨论
3.1 自回归模型参数
由上文可知,在整个极移预报过程中,自回归模型有两个可调节参数,分别是阶数p和间隔数lag.在1-6 d的极移预报阶段,将X分量和Y分量的自回归阶数固定为60阶,使X分量和Y分量的间隔数在区间[1,20]的整数范围内变化,选择符合条件的阶数和间隔数,可以得到354组自回归模型可调节参数,构成了短期极移预报的自回归参数空间.在7-90 d的极移预报阶段,使X分量和Y分量的自回归阶数在区间[2,20]的整数范围内变化,同时,让X分量和Y分量的自回归间隔数在区间[1,20]的整数范围内变化,选择符合条件的阶数和间隔数,同样可以得到354组自回归模型可调节参数,构成了中长期极移预报的自回归参数空间.两个预报阶段参数空间中的不同参数对于极移预报的影响如图4所示.
图4上方的两个子图表明,在1-6 d的短期极移预报中,自回归模型的可调整参数p和lag的选择对于短期极移预报的MAE(Mean Absolute Error)有较为明显的影响,因此,短期极移预报的自回归参数空间中存在更优的参数.同样的,图4下方的两个子图表明,在7-90 d的中长期极移预报中,自回归可调整参数p和lag的选择对于中长期极移预报的MAE有明显的影响,所以,中长期极移预报的自回归参数空间中也存在更优的参数.于是,可以从参数空间中选择出更优的极移预报参数.
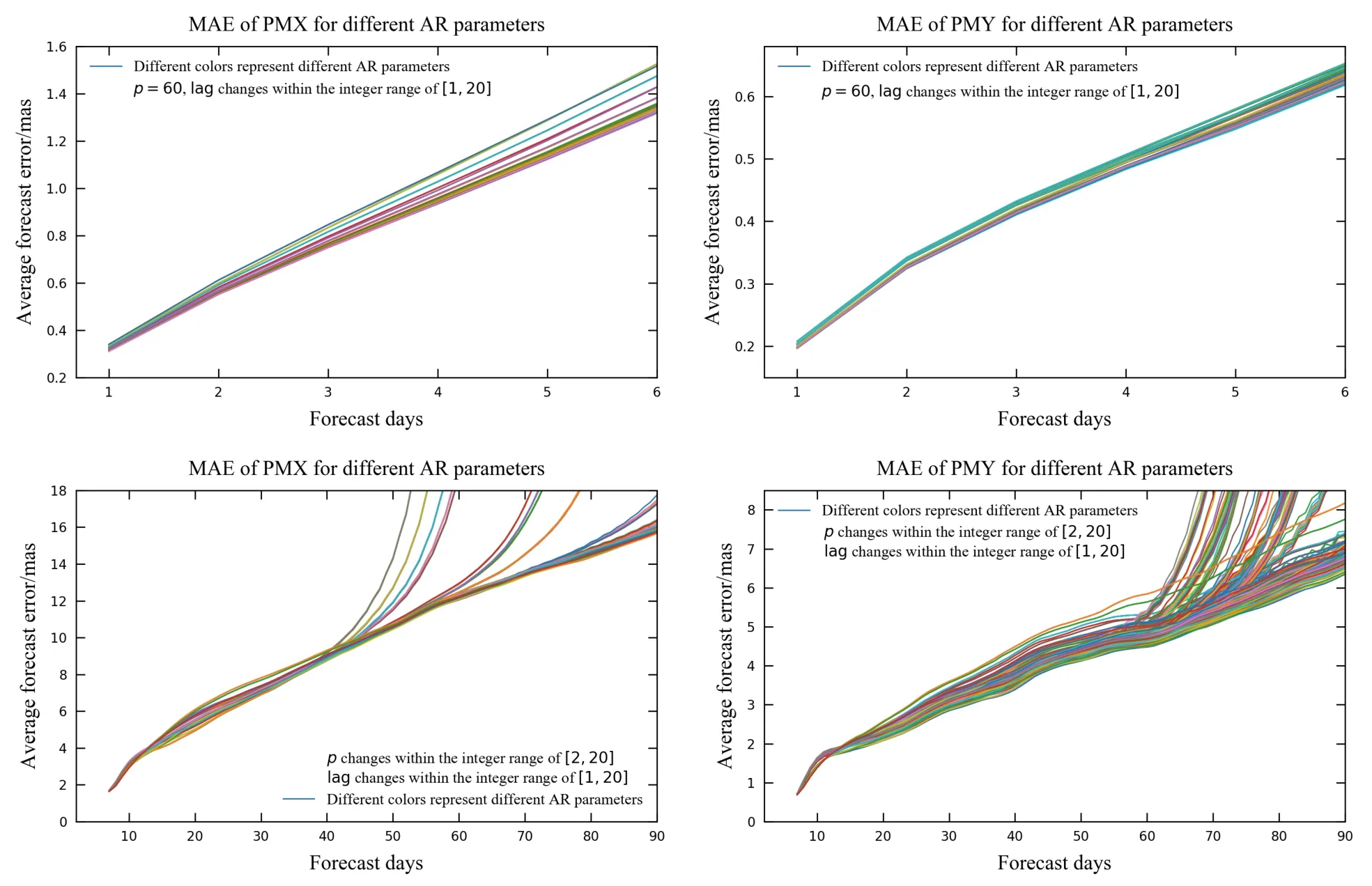
图4 不同的自回归模型参数所对应的极移预报值的MAEFig.4 The MAE of the polar motion prediction values corresponding to different AR model parameters
通过对上述的短期和中长期极移预报自回归参数空间中的参数进行搜索,并且利用多次预报实验比较各组不同参数对于极移预报的影响,就可以选出两组更优的自回归参数,如表2和表3所示.表2-3给出了两组从参数空间中得到的优化参数,其中,表2的参数用于极移X的预报,表3的参数用于极移Y的预报,使得对于不同分量的极移在不同阶段的预报能够采用更优的参数,下文中的预报实验则使用了这两组优化参数.
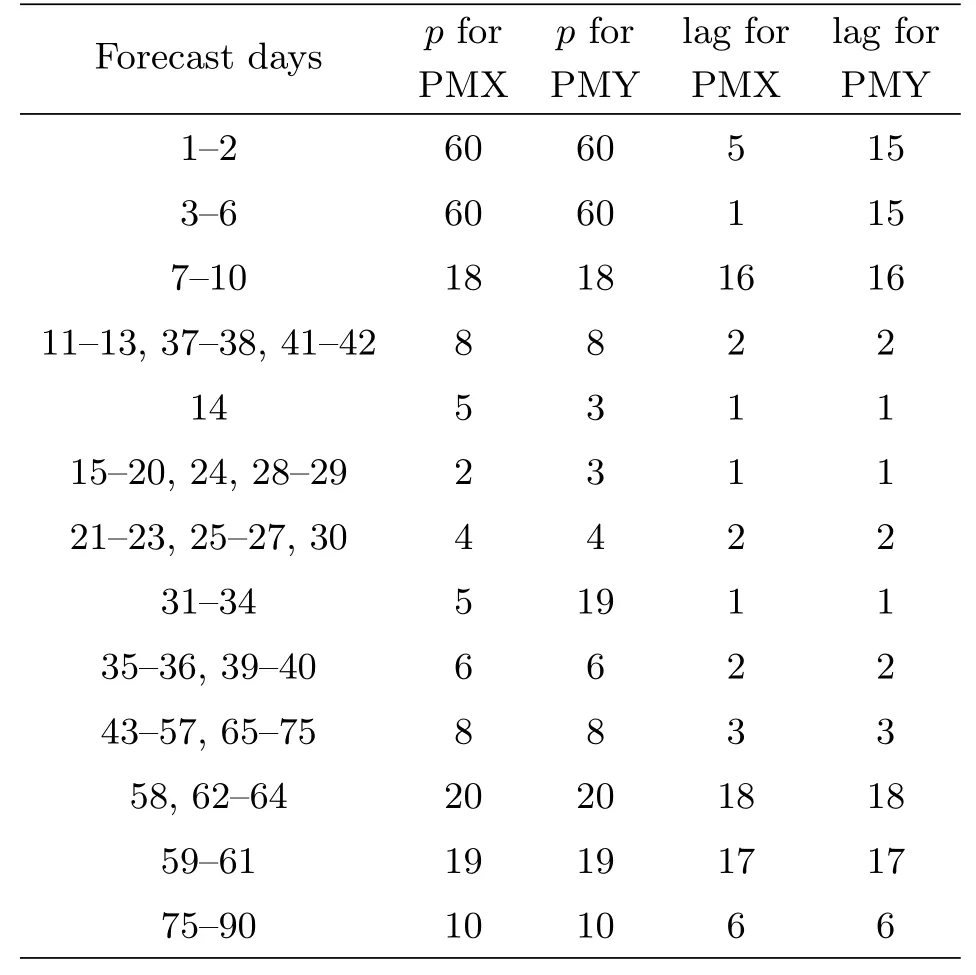
表2 对于极移X预报更优的自回归参数Table 2 Better autoregressive parameters for PMX prediction

表3 对于极移Y预报更优的自回归参数Table 3 Better autoregressive parameters for PMY prediction
由此,对于未来1-90 d中任意一天的极移预报,能够对应一组更优的自回归模型参数p和lag;例如,在预报未来第6 d的极移X时,自回归参数选取为p=(60,60)、lag=(1,15);在预报未来第6 d的极移Y时,自回归参数选取为p=(19,19)、lag=(1,1).可见,为了获得更优的结果,1-90 d的极移预报分别对应多组不同的自回归参数,这同时增加了预报过程中的计算次数,降低了极移预报的计算速度,为了解决此问题,本文采用了不同参数分组并行的计算方法.
3.2 与IERS EOP C04比较
在时间跨度为2019年9月至2021年2月的范围内,采用上文中所述的相关参数,进行了441次极移预报实验,将计算结果与EOP C04提供的极移数据相比较,如图5所示.由图可见,极移X在1-90 d的预报误差分布在0-36 mas的范围内,并且10 d内的预报误差大约在4.5 mas以下;极移Y在1-90 d的预报误差分布在0-16 mas的范围内,并且10 d内的预报误差大约在2 mas以下.此外,极移的预报效果与预报时间段有关,在有些月份预报得好(例如2019年9月),在另一些月份预报得不好(例如2020年8月).

图5 2019年9月至2021年2月之间的441次极移预报实验中1-90 d的预报误差Fig.5 The prediction error from 1 to 90 days in 441 PM prediction experiments between September 2019 and February 2021
3.3 与IERS Bulletin A的比较
在时间跨度为2019年9月至2021年2月的范围内,进行了441次极移预报实验,在实验过程中,采用了上文中所述的相关参数,例如,对于自回归参数的选择,极移X分量的预报中使用了表2所示的参数,极移Y分量的预报中则使用了表3所示的参数.将多次预报结果与Bulletin A提供的极移预报数据相比较(以EOP C04为参考),如图6所示.
由图6可知,整体上,相比于极移X,极移Y的预报优于Bulletin A所占的比例更大.在极移X的预报中,短期有50%以上的预报结果优于Bulletin A,这一比例在第6 d左右达到最大,随着预报日期的增加而下降,30 d之后Bulletin A的预报占据了更多的优势.在极移Y的预报中,短期有60%以上的预报结果优于Bulletin A,同样,这一比例在第6 d左右达到最大,虽然随着预报日期的增加这一比例有所下降,但总体保持在50%以上.由此可见,与Bulletin A相比,极移X的预报在1-30 d更占优势,极移Y的预报则在1-90 d的所有预报阶段均占优势.更进一步,将极移预报划分为3个不同的阶段:1-6 d、7-30 d、31-90 d,以EOP C04为参考,与Bulletin A的比较如图7所示.

图7 极移X预报与Bulletin A的分阶段对比图,白色纹理表示1-6 d的预报阶段,灰色纹理表示7-30 d的预报阶段,点状纹理表示31-90 d的预报阶段.Fig.7 The phase-by-phase comparison of PMX prediction and Bulletin A,the white texture represents the prediction phase from 1 to 6 days,the gray texture represents the forecast phase from 7 to 30 days,and the dotted texture represents the forecast phase from 31 to 90 days.
图7中展示了不同阶段的极移预报与Bulletin A之间的比较,左图表示极移X,右图表示极移Y.横坐标是与Bulletin A之间的差值,即本文相较于Bulletin A的预报精度提升量,其中,负值表示预报误差小于Bulletin A,0值表示预报误差与Bulletin A相差无几,正值表示预报误差大于Bulletin A.以左图为例,在横坐标0值处的白色纹理柱子高度约为45%,那么可以认为有45%的极移X预报与Bulletin A是一样好的;同样的,在横坐标-1处的白色纹理柱子高度约为20%,表明在1-6 d的极移X预报中,有20%的极移X预报误差比Bulletin A小1 mas左右.仍然以白色纹理柱子为例,图中左上角图例的百分比表示在所有的1-6 d的极移X预报中,有56.9%的极移X预报误差要小于Bulletin A.此外,灰色纹理、点状纹理以及极移Y的含义同上.由此可见,在441次预报实验中,极移X的1-6 d预报、7-30 d预报和31-90 d预报比Bulletin A更优的占比分别为56.9%、53.5%和40.5%,并且,大部分预报精度的提升分布在[-3,0]mas的范围内;极移Y的1-6 d预报、7-30 d预报和31-90 d预报比Bulletin A更优的占比分别为66.5%、59.7%和59.2%,并且,大部分预报精度的提升量分布在[-2,0]mas的范围内.
4 总结与展望
本文通过分段最小二乘拟合及改进的自回归模型,使用ESMGFZ提供的数据,提升了1-90 d的极移预报.将AAM、OAM、HAM和SLAM组成的EAM融合进极移的预报,同时,选择更优的自回归模型可调节参数,在多组更优参数的条件下并行预报,从441次极移预报实验来看,极移的预报精度提升是比较明显的.表4为本文中441次预报的MAE(以EOP C04为参考)和Bulletin A相应预报的MAE(以EOP C04为参考)之间的比较.可见,整体上极移Y的预报效果更好;相比于IERS预报,极移X的预报精度在30 d内均有提升,其中,在第1 d和第5 d的提升分别为2.62%和32.98%;极移Y的预报精度在90 d内有明显的提升,其中,在第1 d和第5 d的提升分别为20.77%和48.98%.综上,采用本文中所述的方法,从极移X分量和极移Y分量的角度看,极移Y的预报更有优势;从短期和长期的角度看,短期预报更有优势.

表4 不同阶段的极移预报精度(以EOP C04为参考)Table 4 PM prediction accuracy at different stages(taking EOP C04 as reference)
本文中,极移Y的预报优于极移X的预报,相比于极移Y,极移X的预报误差更大.从有效角动量数据的角度来看,X分量的数据规律性更弱,噪声更大,造成这一现象的主要原因是地球表面的陆地相对于Y轴的分布比X轴更对称.极移的预报结果与时间段也存在着一定的关系,在有些时间段预报得更好,在另外一些时间段预报得不好.在后续的研究中,或许可以通过进一步研究极移的数据特征,寻找更好的最小二乘拟合模型,结合卡尔曼滤波或者人工智能等方法进一步改善极移的预报精度.
致谢感谢Dill博士在本文的研究过程中对于若干问题提供的悉心解答和建议.感谢ESMGFZ和IERS在数据上的支持.

