基于Broyden方法的不对称与对称周期解延拓算法与应用*
徐兴波
(淮阴工学院数理学院应用数学系 淮安 223003)
1 引言
庞加莱(H.Poincar´e)率先用基于隐函数定理的延拓方法来研究限制性三体问题(Restricted Three-Body Problem,RTBP)的周期解,并开创了微分方程定性领域,很多关于周期解的研究都是以庞加莱的方法为根基的.周期解被认为在哈密顿系统有界轨道集合内是稠密的,在很大程度上确定了哈密顿系统相空间的骨架,稳定的轨道对应于有序运动,而不稳定的轨道分布在混沌区域.周期解在非线性动力学研究中具有重要意义,随着理论方法的发展和工程技术的需求,更多复杂的周期解特别是N-体问题的周期解被证明存在、也被计算出来.
周期解问题通常对应于边值问题,给出充分多的定解条件可以确定一个周期解,且只需要知道某个时刻的初值便可将周期解的全部信息计算出来.袁惠群等[1]考虑了非线性自治系统周期解的计算问题,首先将周期解问题化为边值问题,固定部分初值分量,其余初值作为参数,数值积分初值问题可得到对应于周期性条件的非线性方程组,接着利用差商矩阵替代雅可比矩阵,利用拟牛顿法对初值参数做微分改正,求解线性方程组,得到改正值,循环反复直到改正值趋于零且满足精度为止.张锁春[2]综述了关于周期解计算的多种算法,涉及到了庞加莱截面、摄动法、(多重)打靶法、有限差分法、多重网格法、规范型与Hopf分叉、变分与最优控制等方面的知识.庞加莱截面是高维周期解降维计算的常用工具,可将周期解的计算变为截面上不动点的计算.Lindstedt-Poincar´e方法是一种针对含小参数的受摄系统求级数解的摄动方法,数值求解时可以不必展开,这方面的工作可参考Viswanath[3]的工作.
由于很多哈密顿系统存在首次积分和对称性,哈密顿系统周期解的计算不全同于以上这些算法.Farantos[4]给出了基于多重打靶法计算哈密顿系统周期解的算法与程序POMULT(Periodic Orbits MULTishooting),该程序包可以计算周期解、Fourier变换、庞加莱截面、Lyapunov指数等.多重打靶法对高度非线性系统以及不稳定周期解的计算是有效的,它有个特点是需要用压缩算法求解系数矩阵为稀疏矩阵的线性方程组.Lara等[5]针对周期解计算问题的微分改正法,提出了一种基于空间曲线微分几何坐标架的计算方案,并用于计算RTBP的周期解.Wulff等[6-7]先后研究了对称周期解以及哈密顿相对周期解的数值延拓,借助AUTO软件,可以计算三体问题的8-字形周期解,用微分流形方面的数学工具来定义自适应庞加莱截面,并给出了单重和多重两种打靶法来计算不同情形下的周期解.Tsirogiannis等[8]提出了多核并行的网格搜索法,并用于计算Hill问题的全局周期解.Dena等[9]提出了高精度数值延拓周期解的一种方法,该算法包含伪弧长延拓方法(pseudo-arclength)、基于牛顿法的最优打靶法、基于开源软件TIDES(Taylor series Integrator for Differential EquationS)的泰勒级数法以及奇异值分解法(Singular Value Decomposition,SVD).Dena等[10]将这种高精度数值延拓方法与网格搜索、并行计算相结合,应用于计算月球卫星大量周期轨道的初值.Galan-Vioque等[11]回顾了周期解的延拓与周期解稳定性的关系,介绍了边值问题求解软件如何求解对称哈密顿系统周期解的方法,并以数学摆和三体问题8-字形周期解的计算作为验证.
周期解初值延拓计算问题可被转化为边值问题,其中,未知参数包含部分或全部初值,也可以包含周期,并可被蕴含于周期性条件方程组中.问题的关键在于定义周期性条件方程组并求解,但该方程组是动态的:对初值问题进行数值积分,直到数值解抵达某个边界条件,如果周期性条件都满足便得到了周期解初值,如果不满足就要基于微分改正法的思想修正初值,反复这个过程,直到初值收敛且是积分方程组的解.这个非线性积分方程组的求解可以借助数值积分与Broyden方法来完成.对自治与非自治、周期已知与未知、对称与不对称、是否有积分参数、沿着不同参数延拓等不同情形,周期解计算的具体方案有所不同.在一般周期解延拓方法的基础上,基于相关程序[12],本文提出计算一般周期解与对称周期解的一种新方案,并在Linux系统下使用gfortran编程实现,经数值验证,该计算方案是很有效的.
2 一般延拓方法
2.1 微分改正法
考虑N维的常微分初值问题

其中t0是初始时刻,Y=Y(t,Y0)是初值问题(1)式的解,自变量t的定义区间为I⊂R,R为实数域,Y=(y1,y2,···,y N)T∈RN,上标正体符号T表示转置,RN表示每一分量都是实数的N维向量空间,F是(t,Y)∈I×RN映到的函数,这里两个集合相乘的运算是笛卡尔积(以下同).
定义1.称Y(t,Y0)是(1)式所述系统的周期解,如果存在实数T>0,对∀t∈R有Y(t+T,Y0)=Y(t,Y0).其中,T为一个周期,最小正数T为通常所说的周期.
如果有初值Y0,经过约为T0的时间回到初值附近,得Y(t0+T0,Y0)≈Y0,记δY和δT分别为初值和周期的改正值,在改正后得到周期解

为了求得δT和δY,采用微分改正思想进行求解,根据一阶泰勒展开式,


得到

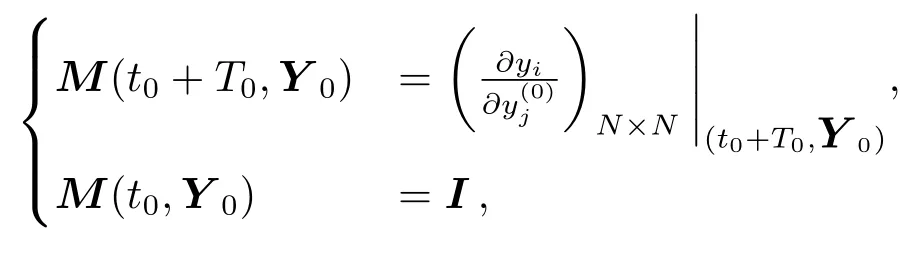
其中,单值矩阵M是解向量Y对初值向量Y0的雅可比矩阵,可以表示为元素(1≤i,j≤N)的集合.为了应用微分改正法求得改正值,需要对(1)式系统中的N个微分方程数值积分,以便得到Y(t0+T0,Y0),同时还需要对微分方程的变分系统

进行积分从而得到单值矩阵M,其中∂F(t,Y)/∂Y为变分矩阵.这样,为得到线性方程组(3),一共需要积分N+N2个微分方程.确定方程组(3)的系数之后,在求解方面仍面临一个关键的问题,即线性方程组(3)有N+1个未知变量而仅有N个方程.为克服该问题,可以利用起始时刻和一个周期后同一个分量的导数相等,增加一个方程来单独改正周期,比如考虑Y第j个分量的导数或者说向量函数F的第j个分量F j在t=t0和t=T+t0时相等.已知第k次迭代计算的初值和周期T(k),得周期改正关系式,
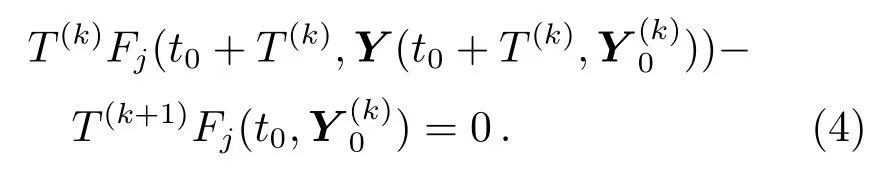
选择F j时,避免F j等于0或接近0的情况,这样可以解出T(k+1).计算δT=T(k+1)-T(k),代入方程组(3)并求解初值的改正值δY,再得+δY.以上过程不断重复,直到改正值满足精度要求.
对微分方程的自变量做适当变换,有时可以提高计算周期解的效果,该方法在多重打靶法中具有重要应用.对系统(1)可以做关于时间t的变换,取τ=mod(t-t0,T)/T∈[0,1],以τ为自变量,得
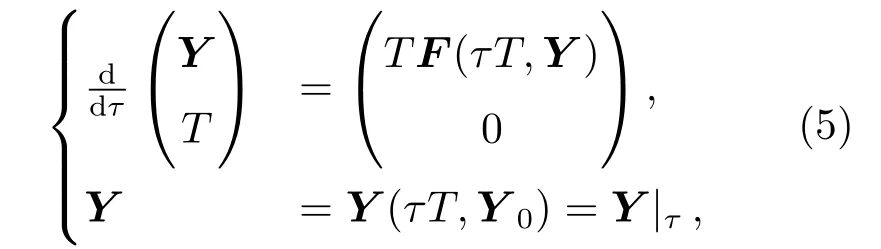
记F|τ=F(τT,Y),以Y0、T0为未知参数,以Y(0)、T(0)为已知参数,初始条件为

N+1维的周期性条件方程组可以写为

交换(6)式中的T和T0不影响求解.
2.2 基于拟牛顿法的算法
如果系统(1)存在周期解,那么方程组(6)存在解.当方程组(6)的雅可比矩阵非奇异时,基于牛顿法(或称Newton-Raphson法)求解方程组(6)是可行的,但为了避免推导变分矩阵和编程的麻烦,使程序面向更多的应用,可以采用差分法来计算系统(1)的单值矩阵,得到方程组(6)的近似雅可比矩阵,再基于牛顿法求解(6),此即拟牛顿法的思想.
已知Broyden方法是一类很有效的拟牛顿法.考虑m维的非线性方程组Φ(X)=0,且Φ:X∈Rm→Rm是Lipschitz连续可微函数.记‖·‖∞为∞-范数,‖·‖2为2-范数,X j为X的第j个分量,那么定义目标函数,求解非线性方程组的Broyden算法如下:
·步0(初始化):迭代次数k=0,初值为X(k),允许误差为eps.
·步1:记Φ(X(k))=Φ(k).若‖Φ(k)‖∞<eps,X(k)即为所求解,返回,算法结束;否则转步2.
·步2:利用向前差分法计算初始雅可比矩阵B(0),第j列为

·步3:根据拟牛顿法,得B(k)δX(k)=-Φ(k),并用正交三角分解法求解,因常用Q表示正交矩阵,R表示上三角矩阵,该分解常被称为QR分解.得到δX(n)后,转步4.

·步4:记X(k+1)=X(k)+λδX(k),线性搜索λ∈(0,1],使目标函数在X(k)处的一阶展开式绝对值最小,

依据是否搜索到λ,分类如下:
步4.1:若得λ,即得X(k+1).若‖λδX(k)‖∞/max(‖X(k)‖∞,1)<eps,返回,算法结束;否则,转步5.
步4.2:若未搜索到λ.令k:=k+1,若k小于最大搜索次数,返回步2重新计算;否则报错,算法结束.
·步5:记两个向量

利用Broyden公式更新雅可比矩阵,⊗表示张量积,

令k:=k+1,转步3.
以上介绍的Broyden方法可以用于求解周期性条件方程组(6),从而得到周期解的初值.
牛顿法具有局部二阶收敛性的特点,在某些凸空间具有非局部收敛性,Broyden同样具备了牛顿法的优点,但用近似雅可比矩阵来寻找下降方向还存在着一些问题,比如,初始近似雅可比矩阵奇异或接近奇异,或者偏离真实雅可比矩阵较多.关于Broyden方法,存在一些改进,对初始雅可比矩阵非奇异情形理论上能够做到算法的全局收敛[13-14].文献[12]提供了结合线性搜索以及可多次尝试计算非奇异初始雅可比矩阵的方法来使用Broyden方法,这种方法的组合增强了求解非线性方程组的有效性.
非线性常微分系统周期解的求解并不是直接调用求解非线性方程组的算法和程序,而是有(a)、(b)、(c)、(d)共4个模块:(a)选择合适的初值和近似的周期并对初值问题进行积分;(b)根据近似的周期确定积分截止时刻并求出对应的解向量;(c)将积分结果代入周期性条件方程组,其中,初值参数的个数和周期性条件方程组的个数是一致的,避免求出奇异的近似雅可比矩阵,这样才得到所要求解的非线性方程组;(d)再利用Broyden类的方法迭代求解该非线性方程组.在程序编制方面,可将(a)、(b)、(c)封装在一起供(d)调用,便可输出满足精度要求的周期性条件方程组的初值参数.
2.3 布鲁塞尔振子算例
为了更清楚地说明如何应用,本节以Brusellator(布鲁塞尔振子)方程[2]为例先进行计算验证.令t、t0、x、y、T、A、B∈R,Brusellator方程为

为了方便在给定初始条件(x(0),y(0),T(0))附近寻找周期解的初值(x0,y0)和周期T0,不失一般性,取初始时刻t0=0,对方程组(7)做时间变量变换,取自变量为τ,满足τ=t/T0∈[0,1],即作如下变元变换,

得周期边值问题,

选取以下3个方程作为周期性条件方程组,

其中x|τ=1,y|τ=1可以由初值问题的数值积分得到.第3个方程被替换为关于周期T的方程,即

求解T,然后再令T0=T,从而周期得到改正,同时数值积分的时间也更新为T.
选择参数A=1、B=3、t0=0时的初值(x0,y0)和近似周期T0为

计算发现,该初值问题的相图接近一个不对称闭圈.由于Brusellator问题的周期解不具对称性,很难做到固定一个分量而只延拓另一个分量就能得到周期解,必须做两个分量的初值延拓.在初始条件附近得到周期解的初值和周期为

数值实验表明,这样的计算方案是可行的.用基于Broyden方法计算周期解初值和周期的方案,对初值相同、周期不同的Brusellator问题,可以延拓得到周期解初值有点偏差的同一个周期解,相图如图1所示.

图1 初始条件为(11)式的Brusellator周期解Fig.1 Periodic solution of Brusellator with initial conditions of Eq.(11)
3 哈密顿系统周期解
3.1 哈密顿系统的对称周期解
如果一个哈密顿系统是含时间的非保守系统,可以通过正则扩充,将时间和哈密顿函数作为一对共轭正则变量,变换得到偶数维的自治系统[15].不失一般性,考虑N维(这里的N为偶数)自治的哈密顿系统H(z)=H(p,q):X⊂RN→R,X为z=(qT,pT)T的定义空间即相空间,q、p分别为广义坐标和广义动量,对应的微分方程组为
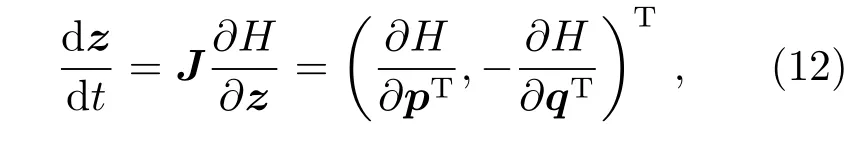
其中J为N阶反对称矩阵,可分为4个子块,左上、右下为零矩阵,右上为负的单位矩阵,左下为单位矩阵,且满足JT=-J=J-1.
定义2.称矩阵Γ为反辛的,如果ΓTJΓ=-J.如果哈密顿系统H(z)满足H(Γz)=H(z),Γ2=I,那么反辛矩阵Γ为H(z)的一个离散辛对称.
引理3.考虑哈密顿系统(12),记该系统在时刻t0的初值为z0,那么它的解z可表示为z=z(t,z0),满足z(0,z0)=z0.如果Γ是它的一个离散辛对称,满足

那么必然存在对称周期解z(T,z0)=z(0,z0)=z0.
证由已知条件,有

如果哈密顿系统存在周期解,取与某处相流z横截的超平面为庞加莱截面Πz,周期解便对应于该截面到自身映射的不动点.记Πz为离散辛对称哈密顿系统的一个对称轴或对称平面,那么两次垂直通过Πz的解为对称周期解.由于周期是未知的,可以设定初值使之满足垂直通过条件,仅需要判断第2次通过是否垂直,但需要借助较为准确的插值确定抵达Πz的时间,然后通过延拓方法修正初值,如此反复,直到初值满足要求.
3.2 解的插值与延拓
为较有效地计算解向量第2次通过Πz的时间,可采用两向量的Hermite插值.采用单步法对系统(12)进行数值积分,记前一步没有通过Πz的时刻为t b=0,而后一步却在Πz上或通过Πz,记该时刻为t a=t b+h,实际上,h>0为解穿过Πz的单步积分时长,记ξ=∈[0,1].再记

整理得Hermite插值的一元三次多项式向量P(ξ),


如果z的某个分量方向恰好通过Πz,则选取P(ξ)的该分量为0,利用一元三次方程求根公式(盛金公式)即可得出实根ξ0∈(0,1),再利用P(ξ0)可求出其他分量在此刻的值.
要求改正后的初值满足从截面Πz垂直出发的条件,即

可将该方程作为一个约束条件用于修正初值.

得线性方程

以上内容介绍了对称周期解的延拓计算方法以及考虑能量守恒系统的单参数周期解的计算方案,下面将以RTBP的周期解计算来验证算法的可行性与有效性.
3.3 PCRTBP周期轨道分类
经典的RTBP是指一个质量可以忽略的小天体在两个可看作质点的大天体的万有引力作用下的运动问题,在不同的坐标系下被写成不同的不可积哈密顿形式,至今仍是很多哈密顿系统理论和方法的试金石[16].
两个大天体的相对轨道为圆型时,这便得到了圆型RTBP.考虑平面圆型RTBP(Planar Circular RTBP,PCRTBP),记大天体为P1、P2.以两大天体的质量和为质量单位,以大天体之间相对轨道(圆型轨道)半径为长度单位,以两个大天体相对轨道的平均运动角频率的倒数为时间单位,使得万有引力常数G在此单位制下恒为1.在归一化的单位制下,P1、P2的质量分别为1-μ、μ.
在大天体运动平面上,以P1为坐标原点,选定某时刻从P1指向P2的方向为横轴(x1轴)正方向,可建立右手螺旋直角坐标系,此即P1心旋转坐标系,记小天体的位置坐标为x=(x1,x2)T,与x共轭的广义动量为

记‖·‖为表示向量长度的2-范数运算符.利用P1心旋转坐标系与质心旋转坐标系之间的换算关系,可计算得到P1心坐标系下的哈密顿函数,
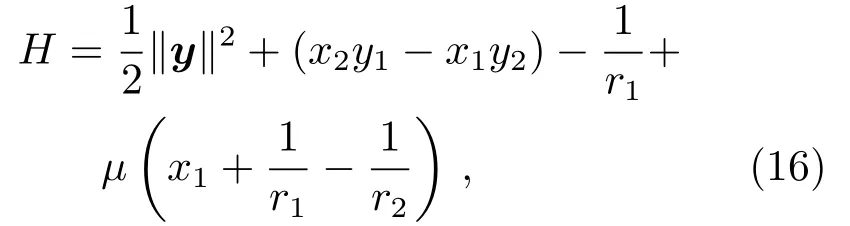
其中r1=‖x‖,r2=‖x-(1,0)T‖.对应的微分系统为

该系统关于大天体连线即x1轴对称,离散辛对称矩阵为Γ1=diag{1,-1,-1,1}.
RTBP中μ=0的未受摄系统的周期轨道也称派生(generating)轨道,均以单参数的解族形式存在.Poincar´e依据延拓法,以μ=0的未受摄系统的周期解类型来对RTBP的周期解进行分类.Bruno等在Poincar´e分类的基础上对PCRTBP的周期轨道做了更详细的研究.以μ为小参数,第1种(1st species)周期轨道是指延拓未受摄系统圆型或椭圆型周期轨道得到的周期轨道.若未受摄系统的周期轨道为:(1)平面圆型,此为第1类(1st kind);(2)平面椭圆型,此为第2类(2nd kind).另外,在惯性坐标系中,如果小天体沿着大天体的绕转方向运动,称之为顺行(direct motion);如果相对静止,称之为相对平衡;如果与大天体的绕转方向相反,称之为逆行(retrograde motion).不经过P2的派生轨道为第1种;绕P1运动且经过P2的派生轨道为第2种(2nd species);局限于P2附近的派生轨道为第3种(3rd species).
当μ=0时,记小天体绕P1的轨道周期为T,平运动为|n|,

当小天体顺行时,n为正,逆行时为负.小天体轨道的平近点角为

小天体的轨道半长径为a,满足n2a3=1,即a=|n|-2/3.在PCRTBP第1种派生轨道中,第1、2类周期轨道按照顺行、逆行以及形状等又划分为不同的型(genre).
给第1类圆型轨道族命名时,Circular的首字母C常用作雅可比积分,故采用第2个字母大写来命名,另外I也形似1.下标的命名,采用了英文首字母:顺行记d,逆行记r,靠内(interior)记i,靠外(exterior)记e.当n>1时,0<a<1,轨道为顺行、内轨道,下标记为di;当0<n<1时,a>1,轨道为顺行、外轨道,下标记为de;当n<0时,轨道为逆行的,下标则记为r.给第2类椭圆轨道族命名时,取Elliptic的首字母命名.下标以P2和小天体的整数周期比来命名;上标的取法按照定义执行,其中上标a代表asymmetric的首字母.
定义4.[17](1)第1类轨道分为3个型:顺行内轨道Idi、顺行外轨道Ide、逆行轨道Ir,轨道解为x1=acos(ℓ-t),x2=asin(ℓ-t).
(2)第2类轨道分为5个型.记天体P2和小天体绕大天体P1顺行运动的圈数分别为互质整数I、J(逆行时为负数).小天体轨道的半长径为a=(I/J)2/3,偏心率为e(0<e<1),称轨道为型、型的,如果I+J为奇数,轨道与正x1轴分别在(0,a)、(a,2a)内有一次垂直相交.称轨道分别为型、型的,如果I、J同为奇数,分别与正x1轴、负x1轴有两次垂直通过.称不关于x1轴对称的轨道为型的(J=1).其中,对称轨道垂直通过正x1轴,x1=a(1±e),
3.4 PCRTBP对称周期解的计算
在延拓计算对称周期解时,本文算法没有用派生轨道的周期来控制积分截止时刻,因为受摄系统的轨道未必在派生轨道的半个周期后能垂直靠近对称轴;如果按照一个周期条件来延拓初值,便失去了对称性约束.考虑PCRTBP的对称周期解的计算,以μ为小参数,P2和小天体在惯性坐标系下分别顺行绕P1转I、J圈,那么在旋转坐标系下,小天体有2|J-I|次经过x1轴.延拓的周期轨道仍与派生轨道具有相同的对称性,经过x1轴的次数也相同.根据引理3,只需要计算半个周期的信息就可以延拓对称周期解.周期未知,但能计算经过对称轴的次数.从初值作为第1次垂直通过x1轴算起,到第1+|J-I|次通过x1轴结束,如果第1+|J-I|次是垂直x1轴的,那么周期解初值已经找到,否则应用Hermite插值得到x2=0的时刻T0/2作为临时的半个周期.利用前后两次经过x1轴的积分结果进行Hermite插值,得到类似于(6)或(9)式的半个周期的周期条件方程组,

并可应用Broyden方法延拓得解.对称周期解能否成功延拓,关键在于能否找到(17)式的解.影响成功延拓的因素有多方面,主要包括周期解的稳定性、解的计算精度、周期性条件、非线性方程组求解算法、代码本身等.下一段将对这些因素进行简要的说明.
(1)周期解的稳定性依赖于初值和小参数.若周期解是稳定的(比如线性稳定),稳定的周期解附近仍存在大量的周期解,满足精度要求下数值积分的步长可以大一些,小参数的变化可以比较大.当计算对称周期解时,可用插值法来计算某解分量再次抵达超平面Πz的解,该解可用一次Hermite插值来估计,将插值解代入周期性条件方程组,在一定精度范围内能够成功延拓周期解.若周期解是不稳定的(比如单值性矩阵的一对特征值即一对特征乘子互为倒数),周期解对初值和小参数的敏感性比较强,待延拓的小参数的变化如果不充分小,采用变步长的数值积分并用插值法来估计某解分量再次抵达超平面Πz,存在的误差有可能影响周期性条件方程组的精确求解.(2)两点的Hermite插值精度与区间长度有关,误差量级为区间长度的4次方.如果对周期性条件方程组的求解精度要求较高,就要选择适当的初始积分步长,既要避免数值积分累计误差过大,也要降低插值误差.(3)如果计算对称周期解,就需要利用对称条件来建立周期性条件方程组,否则得不到对称解.而且周期性条件方程组的方程个数必须与未知初值参数的个数相同,否则计算不出雅可比矩阵.(4)在2.2节的结尾已经作了说明,结合线性搜索、可多次计算初始雅可比矩阵以及用QR分解的Broyden方法对精确的积分型非线性方程组求解是全局超线性收敛的.
下面结合具体算例来叙述一些计算细节.选择以μ为小参数延拓第2类派生轨道来作为算例,考虑延拓后的小参数μ=0.001,并考虑P2与小天体平运动之比I/J等于1/(±2)或1/(±3),派生轨道的周期都为2π,并固定派生轨道的偏心率、轨道倾角、升点经度、近点角距依次为e=0.1、i=0、Ω=0、ω=0.由于考虑到顺行、逆行、近点、远点的情况,得到垂直通过正x1轴的4种初值:(1)近点顺行;(2)近点逆行;(3)远点顺行;(4)远点逆行.初值的形式均为(x1,0,0,),其中x1、与轨道根数的关系见定义4.
对PCRTBP,考虑μ=0.001,延拓I/J=1/(±2)的派生轨道,得到的结果见表1,其中斜体E为偏近点角,|n|为平运动,带上标*的值为对称周期解参数,数值图像见图2;延拓I/J=1/(±3)的派生轨道,得到的结果见表2,数值图像见图3.数值发现积分步长影响计算结果,原因主要在于插值尽管节省时间但存在一定的误差,共振不稳定的解对初值具有敏感性,使得不同初始积分步长情况下得到的周期性条件方程组略有不同,所以使用不同步长延拓的共振周期解可能不同.经验表明,步长可以选择一个较小值比上积分圈数,比如0.01/(1+|J-I|),如果初值和积分一个周期后的值之间的绝对误差超过10-10,可以适当缩小初始步长,使得周期性条件方程组两端误差的最大值不超过10-10,这样得到的周期解精度较高.算法表现出了较好的执行效率,表1-2的最后一列记录了在4核8G内存、i7-6500U CPU上延拓计算所需时间(单位为s).图2中,4个轨道都满足I+J=1+2=3为奇数,左侧的轨道都是顺行,右侧的轨道都逆行;左上侧的轨道与正x1轴有一次垂直通过,且交点横坐标在(0,a)内,属于解族;左下侧的轨道与正x1轴也有一次垂直通过,交点横坐标在(a,2a)内,当属于解族;右侧轨道与正x1轴均有两次垂直通过,由于偏心率e=0.1,使得两次垂直通过分别介于(0,a)、(a,2a)范围内,可知右上侧轨道属于解族;右下侧轨道属于解族.图3仅提供了两幅子图,原因是此情况下近点处的延拓轨道与远点处的延拓轨道形状完全相同,左、右轨道分别属于解族、解族.

图2 μ=0.001情形下的族周期轨道相图(顺行时类型上标为“i”,逆行时上标类型为“e”).派生轨道半长径a=,偏心率e=0.1,近点角距ω=0.左上图顺行,n=2,偏近点角E=0;右上图逆行,n=-2,偏近点角E=0;左下图顺行,n=2,偏近点角E=π;右下图逆行,n=-2,偏近点角E=π.Fig.2 The phase diagrams of the periodic orbits infamilies atμ=0.001(the upper symbol is“i”when the motion is direct,and“e”when the motion is retrograde).The semi-major axis of the corresponding generating orbit is a=,the eccentricity is e=0.1,and the argument of the pericenter isω=0.The upper left panel is for the prograde motion with mean motion velocity n=2 and initial eccentric anomaly E=0;the upper right panel is for the retrograde motion with n=-2 and E=0;the lower left panel is for the prograde motion with n=2 and E=π;the lower right panel is for the retrograde motion with n=-2 and E=π.
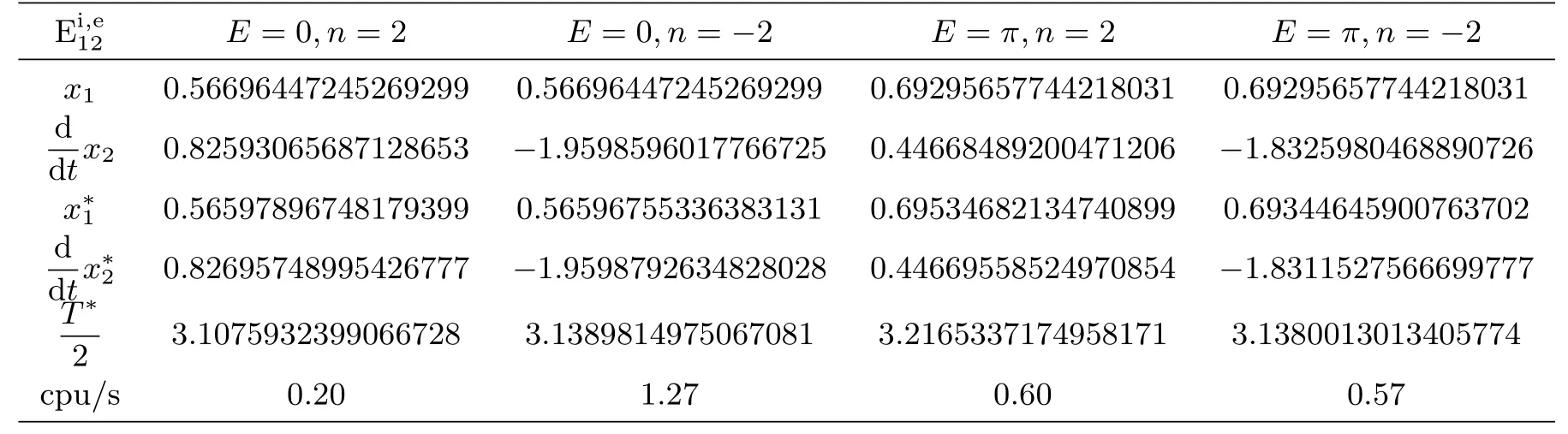
表1 2/1周期比的派生轨道在μ=0.001时延拓得到的对称周期解信息Table 1 Information of the symmetric periodic solution atμ=0.001 continued from the 2/1 resonant generating orbit

表2 3/1周期比的派生轨道在μ=0.001时延拓得到的对称周期解信息Table 2 Information of the symmetric periodic solution atμ=0.001 continued from the 3/1 resonant generating orbit
另外,可以利用数值方法计算出单值矩阵的特征值来了解这些周期解的线性稳定性.以上几个初值问题的线性变分系统各有4个特征乘子,一对为模小于1的共轭复根,另一对为互为倒数的实根或互为共轭的复根(有一个模大于1),以上计算得到的周期解都是线性不稳定的.
4 总结与讨论
在介绍一般周期解延拓方法的基础上,回顾了基于牛顿法的微分改正法,并阐述了一种对求解非线性方程组行之有效的Broyden方法.该Broyden方法并不单单指用差分法来近似计算雅可比矩阵,而是包含了线性全局搜索、可尝试多次计算雅可比矩阵、用QR分解法来减少求解线性方程组的计算复杂度等优点,该方法对求解非线性方程组来说是一种全局收敛方法.但周期解的周期性条件方程组并不是一个确定好了的方程组,而是经数值积分得到且使得周期性条件方程组近似成立.

图3μ=0.001情形下的族周期轨道相图(顺行轨道上标为“+”,逆行时上标为“-”).派生轨道半长径a=,偏心率e=0.1,近点角距ω=0.左图顺行,n=3,偏近点角E=0,π;右图逆行,n=-3,偏近点角E=0,π.Fig.3 The phase diagrams of the periodic orbits infamilies atμ=0.001(“+”for the prograde motion,and“-”for the retrograde motion).The semi-major axis of the corresponding generating orbit is a=,the eccentricity is e=0.1,and the argument of the pericenter isω=0.The left panel is for the prograde motion with the mean motion velocity n=3 and the initial eccentric anomaly E=0 orπ;the right panel is for the retrograde motion with n=-2 and E=0 orπ.
一般的周期解没有对称性约束,需要积分接近一个周期的时间,将周期作为待延拓的参数,不断延拓初值和周期,最终得到收敛参数.对称周期解的延拓需要利用对称性,否则所得的周期解未必是对称的.根据哈密顿的离散辛对称性,两次垂直通过超平面的解是对称解,那么只需数值积分计算半个周期的信息便可延拓初值.初值在超平面上,待延拓的初值参数在该超平面的补空间上,根据某一分量的符号变化来判别何时抵达超平面附近,利用超平面两端节点进行Hermite插值,求解一元三次方程,得到该分量抵达超平面的时间,待延拓的初值参数可以通过插值得到.如果相空间的维数大于4,可以固定一个待延拓初值参数.PCRTB相空间维数为4,如果固定一个待延拓初值参数,最后得到的雅可比矩阵的秩便等于1,这在程序实现时会带来矩阵调用报错的问题.可设满足在超平面上的分量都等于零,同时,为了方便获得周期,将周期作为待延拓参数,设半个周期减去第2次抵达超平面的时间等于零,这便得到周期性条件方程组.
在调用程序计算周期解时,发现数值积分步长对周期解初值的求解精度有一定的影响.积分算法和Hermite插值的精度都依赖于步长,Hermite插值的误差为步长的4次方量级.积分步长较小,插值比较精确,但积分累计误差较大,计算时间也长,而积分步长较大,积分累计误差小,但积分和插值也有误差.数值实验经验显示,对不稳定的共振周期解的计算,变步长RK(Runge-Kutta)78的初始积分步长可以选择区间[0.001,0.02]上的值.另外,今后可以结合比较二分法与Hermite插值对数值延拓效果的影响.
在计算PCRTBP的周期解时,选择简单的共振比2/1和3/1来作为计算对称周期解的约束条件.从摄动小质量为0的未受摄系统的派生轨道的初值开始延拓,延拓时选择小质量参数为μ=0.001.根据H´enon的周期轨道分类,将顺行或逆行、初值在近点或远点这4种情况的椭圆型周期轨道都做了计算,发现2/1共振顺行、逆行轨道分别属于族、族;3/1共振顺行、逆行轨道分别属于族、族.还发现,这些周期解都是线性不稳定的,线性变分系统的特征乘子有一对共轭复根,它们的模小于1,另一对互为倒数或互为共轭,有一个特征乘子的模大于1.顺行的不稳定性强于同等条件下的逆行情形,2/1共振的不稳定性强于同等条件下3/1共振的稳定性,多数情况下近点作为初值的解的不稳定性强于同等条件下远点作为初值的解的不稳定性.关于其他周期解的计算和对稳定性的分析也将是下一步值得考虑的工作.
今后关于周期解研究的工作可能有3方面:理论上,除了延拓方法,还可以考虑使用变分方法、稳定性理论等;数值上,可以引入现代优化方法、高精度积分工具等;应用上,结合天文背景可以将相关研究推广到应用领域.
致谢作者衷心感谢审稿人的评审意见和编辑的修改意见.

