基于集成学习的FRP 加固混凝土梁抗弯承载力预测研究

张书颖，陈适之，韩万水，吴 刚

(1. 长安大学公路学院，西安 710064；2. 东南大学土木工程学院，南京 210096)

随着公路桥梁服役年限增加，上部交通荷载吨位不断上升，大量在役混凝土桥梁性能不可避免的发生退化，导致可靠度降低，形成了巨大的安全隐患。因此为确保在役桥梁安全，研发相应的高效加固方法意义非凡。

FRP 材料具有轻质高强、耐久性好等优点[1-2]，且施工方便，广泛应用于钢筋混凝土(reinforced concrete, RC)结构加固[3-5]。现有FRP 加固RC 梁方式主要包括外贴式[6-7]、端锚式[8-9]和嵌入式[10-11]等。加固后RC 梁的抗弯承载力受到包括梁体截面尺寸、混凝土、钢筋、FRP 材料性能、FRP 截面面积及加固形式等诸多因素影响，加固后的梁体也存在多种潜在破坏模式，致使加固后RC 梁抗弯承载力预测要考虑的情况复杂且参数众多[12-13]。已有的理论公式在实际应用中过于繁琐且存在较大误差，导致无法基于既有RC 规范对FRP 加固后桥梁抗弯承载力进行准确设计评估[14]。为研究FRP 加固后RC 梁性能，建立相应的抗弯承载力预测模型，过去几十年间，国内外学者们已开展了大量试验研究，涉及多种FRP 加固方式[15-17]。

目前，针对工程中最常用的外贴式加固，我国出台了相关技术标准进行加固后RC 梁承载力计算[18]，此外，有学者在大量试验研究的基础上，考虑多种破坏模式，对加固后RC 梁受力状态进行理论分析，提出了外贴式FRP 加固RC 梁的抗弯承载力计算公式[19-20]。对于嵌入式加固，研究人员在RC 梁抗弯承载力计算公式上进行改进，提出了FRP 嵌入式加固梁抗弯承载力计算公式，并通过试验进行验证[21-22]。而对于端锚式的加固方式，多使用外贴式加固后梁抗弯承载力预测模型进行简化计算[18]。此外，针对不同的FRP 加固方式，统一的计算模型仍较为缺乏，导致设计计算过程繁琐，不利于工程使用，且现有理论预测模型多基于力学简化假设，在应用中预测精度往往不稳定，泛化能力有限[14]。因此，亟需建立一种适用于多种加固方式高效准确的FRP 加固钢筋混凝土梁抗弯承载力预测模型。

近年来机器学习方法逐渐兴起[23-24]，它可以基于既有实测数据，通过训练学习数据内的深层规律得到可靠的预测模型，并表现出良好的泛化性能[25-26]，吸引了大量研究人员的关注[27-28]，被广泛应用于工程领域中[29-30]。目前，已有学者将机器学习算法应用于混凝土构件基本力学性能预测[31-32]。针对梁的抗弯承载力预测，有研究人员使用神经网络等机器学习算法进行预测，并取得了较好的效果[33-34]。Naser 尝试基于人工神经网络和遗传算法建立FRP 加固梁抗弯承载力的显式预测公式，并对公式进行了验证[14]。但该研究只建立了外贴式和嵌入式两种加固方式的统一计算公式，无法用于另一种常见的端锚式加固方式。同时该研究最终使用显式函数拟合FRP 加固RC梁抗弯承载力，得到的计算公式复杂，计算过程繁琐，不利于实际应用，一定程度上也损失了机器学习预测模型的精度。

在此背景下，为提升FRP 加固RC 梁抗弯承载力预测的便利性和准确性，本文利用集成学习算法XGBoost，基于文献中收集的既有FRP 加固RC 梁试验样本数据集，建立起统一的FRP 加固RC 梁抗弯承载力预测模型，可同时适用于外贴式、端锚式以及嵌入式等不同的FRP 加固方式。文章具体内容如下：第一部分对既有FRP 加固方法及收集的样本集进行说明；第二部分对选用的集成学习算法XGBoost 进行介绍；第三部分通过训练样本集，建立基于XGBoost 的FRP 加固RC梁抗弯承载力预测模型，随后在测试样本集上与基于SVR 和ANN 两种典型机器学习算法建立的预测模型进行横向对比，同时分析了不同加固方式下的模型精度，验证本文提出模型的精度和泛化能力，最后分析了输入参数的特征重要性，说明了该模型的合理性。

1 FRP 加固混凝土梁

1.1 FRP 加固方法

与传统的工程材料相比，FRP 材料具有轻质高强、耐腐蚀、耐久性好、易施工等优点。

由于FRP 材料的这些优异性能，它被广泛应用于加固既有RC 桥梁。目前工程上常见的加固方式包括：① FRP 外贴式加固，将FRP 布或板材外贴在梁底部；② FRP 端锚式加固，在FRP 初步固定在梁底的基础上，两端使用钢板锚或U 型箍固定；③ FRP 嵌入式加固，将FRP 筋或板材嵌入梁上预先开好的槽中，向槽内注入粘结材料使FRP与梁共同受力。三种加固方式如图1 所示。

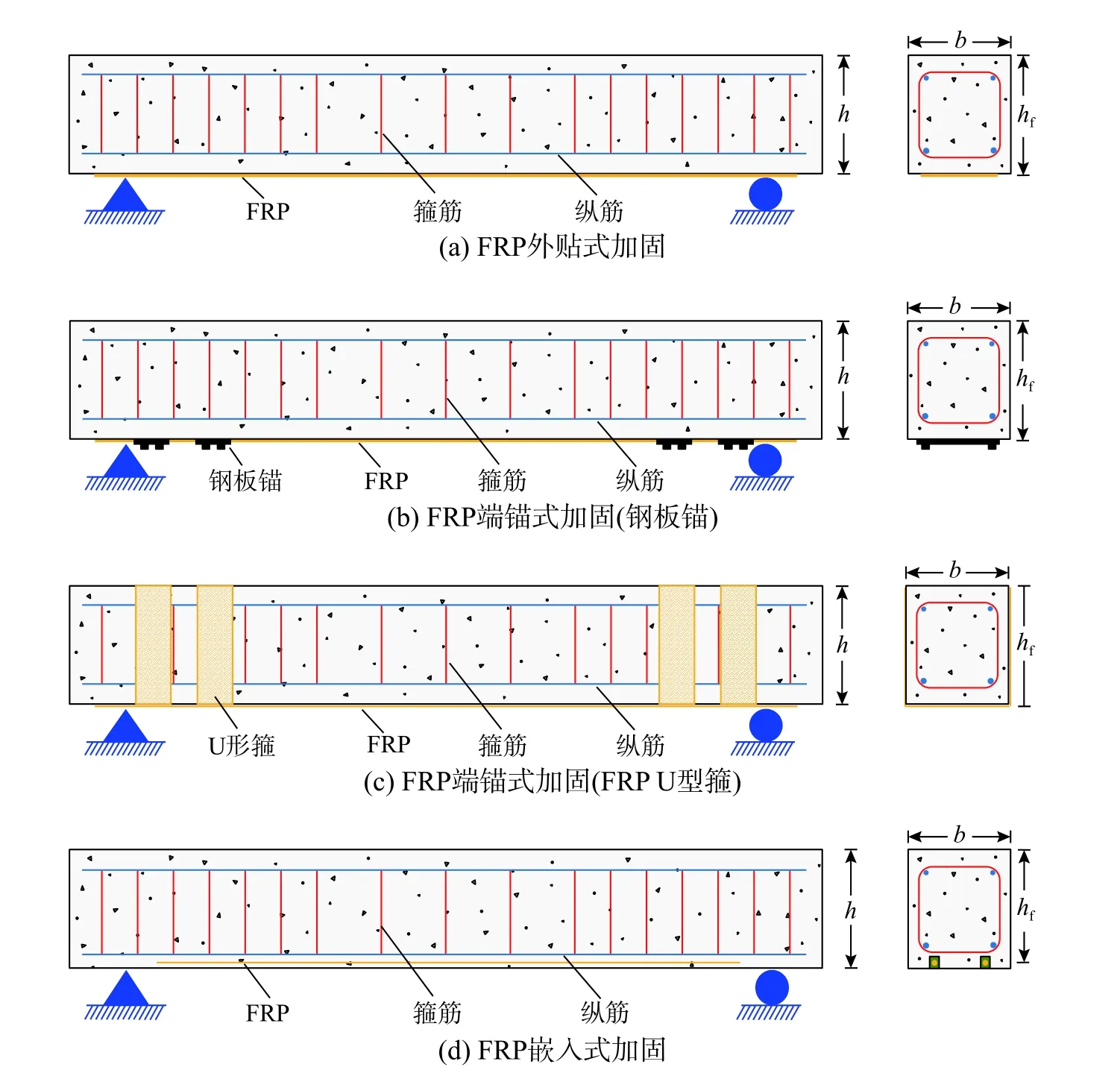
图1 FRP 加固RC 梁示意图Fig. 1 RC beams strengthened with FRP

1.2 FRP 加固数据

通过搜集既有FRP 加固相关文献，建立的数据集包含153 组试验数据(数据来源见参考文献[8 - 10, 15 - 17, 35 - 66])。其中包括42 组FRP 外贴式加固样本、58 组FRP 端锚式加固样本以及53 组FRP 嵌入式加固样本，破坏方式涵盖受压区混凝土压溃、粘结破坏、FRP 拉断以及FRP 剥离破坏等。

基于既有研究，影响FRP 加固RC 梁抗弯承载力的因素，除梁截面尺寸、钢筋强度和配筋率等与普通RC 梁相同的因素外，还包括FRP 材料性能及用量等因素。因此，本次承载力预测模型选定的输入参数包括：混凝土立方体抗压强度fc、钢筋屈服强度fy、FRP 材料抗拉强度ff、FRP 材料弹性模量Efr、纵向钢筋配筋率rs、FRP 材料配布率rf、梁宽b、梁高h。模型输出为FRP 加固RC梁破坏时跨中弯矩M。

其中FRP 材料配布率rf计算方法如下式：

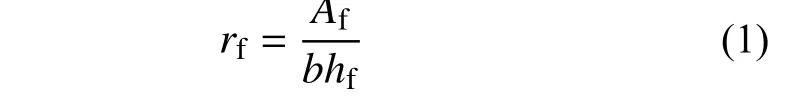
式中：Af为FRP 材料横截面面积；b为RC 梁的宽度；hf为FRP 中心距离梁顶的距离。

表1 为数据集中各项输入输出参数的统计特征，图2 展示了数据集中输入参数与FRP 加固RC 梁的抗弯承载力之间的关系。综合二者可以看到，数据集离散程度大、取值涵盖范围广，同时各参数分布较为均匀，因而可为建立基于数据驱动的抗弯承载力预测模型提供可靠的数据基础。

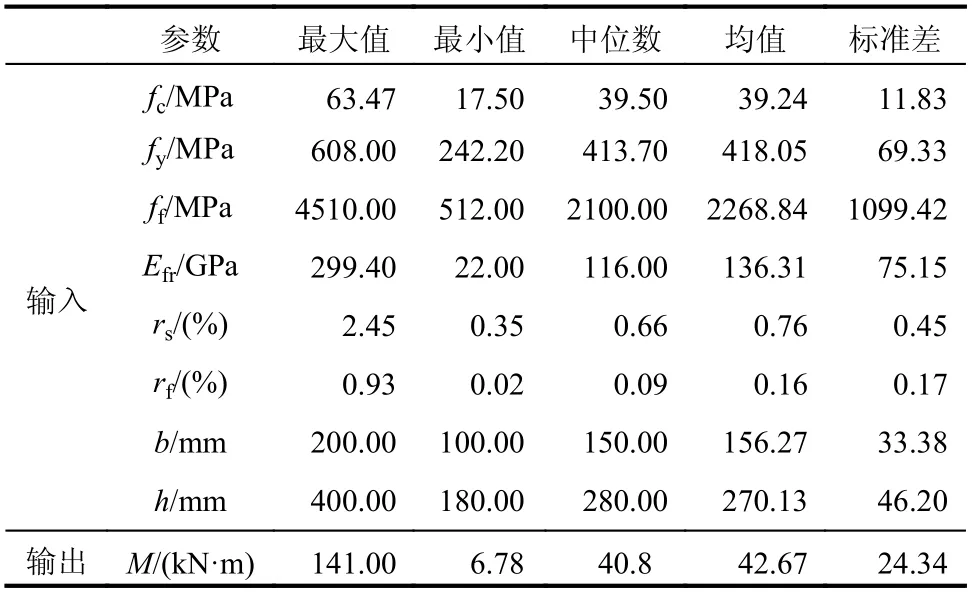
表1 FRP 加固样本集参数统计特征Table 1 Statistical characteristics of FRP strengthened sample parameters

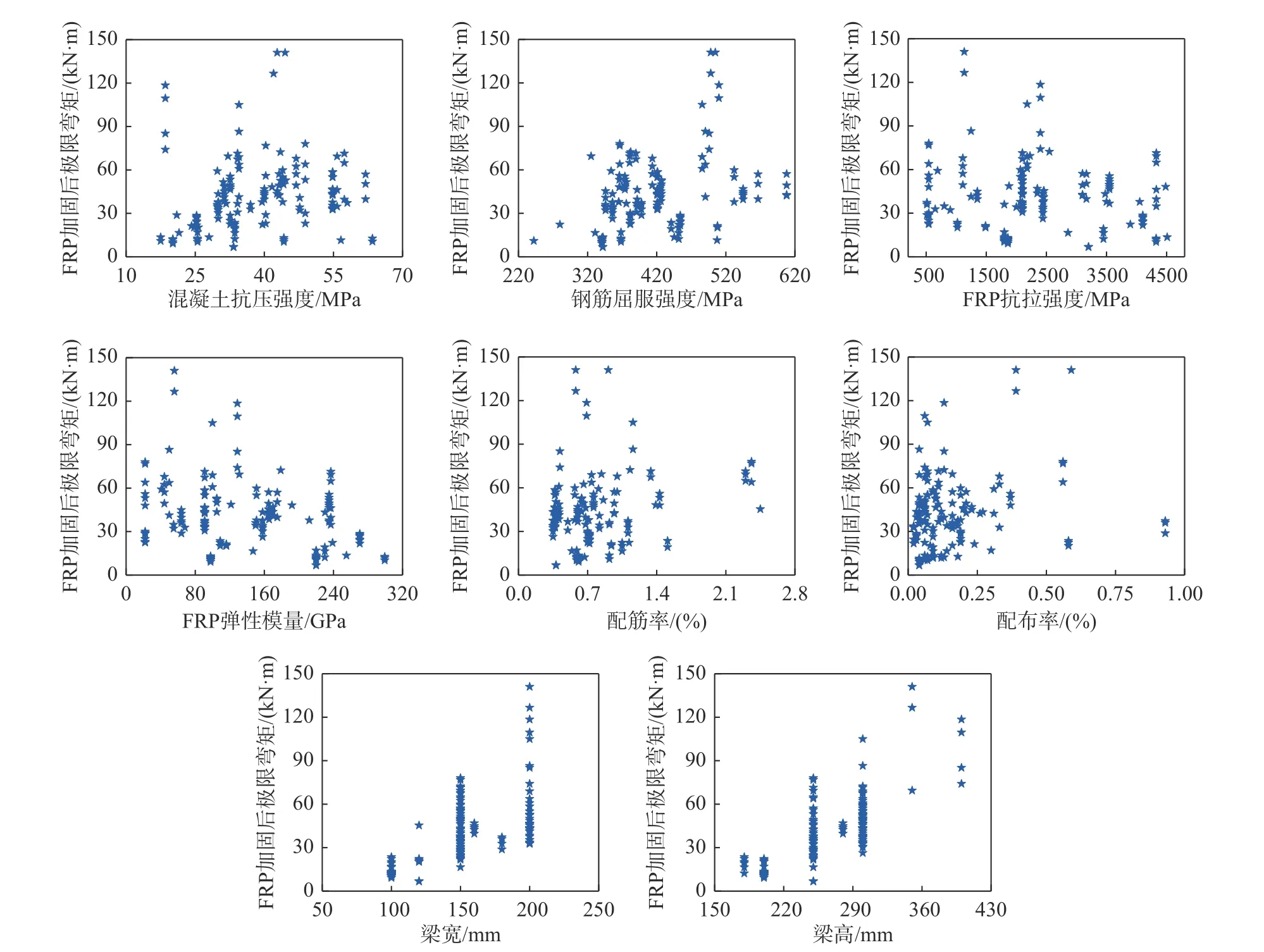
图2 FRP 加固后承载力与输入参数关系Fig. 2 Variation of the bearing capacity with the input parameters after FRP strengthened

2 集成学习

机器学习算法可以从数据中自适应学习输入、输出间的映射关系，相较于传统经验公式拟合拥有更高的识别精度。而集成学习作为机器学习的延伸，通过有机集成多个性能各异的基学习器来完成分类或回归任务，相比于单个机器学习算法，具有更高精度及泛化能力[67]。

极限梯度提升树(extreme gradient boosting,XGBoost)算法作为目前集成学习算法的代表，以决策树作为基学习器，通过整合多个决策树的预测结果得到最终输出结果[68]，具体如下式：

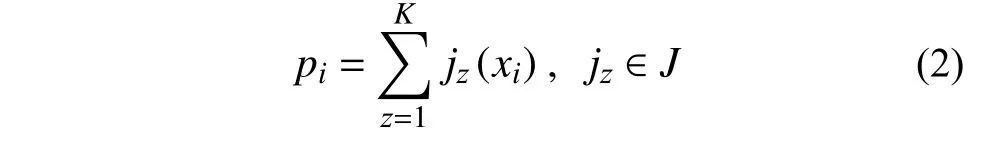
式中：pi为第i个目标的预测值；K为树的数目；jz为树结构和树叶权重函数，每个jz对应一个独立的树模型；J为决策树的值域。

XGBoost 算法的基本思想是顺序学习，即将当前决策树与当前已集成决策树的残差进行拟合，随后将新生成的决策树加入算法序列中从而降低模型整体残差[69]。其目标函数由损失函数项和正则项组成。损失函数描述了算法预测偏差，正则项的作用在于抑制算法复杂度，防止过拟合。XGBoost 算法的目标函数可表示为：

式中：Obj为目标函数；N为总样本量；l(yi,pi)为损失函数即目标预测值与实测值间的差值；yi为第i个目标的实测值；Ω为决策树的复杂度。

训练目标为最小化目标函数，将损失函数泰勒展开至2 阶，令第t轮迭代得到的目标函数导数为0，即得到目标函数最小值，相应得到最优算法。

3 模型训练与结果讨论

3.1 模型训练流程

按照如图3 所示工作流程，建立出基于XGBoost的FRP 加固RC 梁抗弯承载力预测模型。具体说明如下：

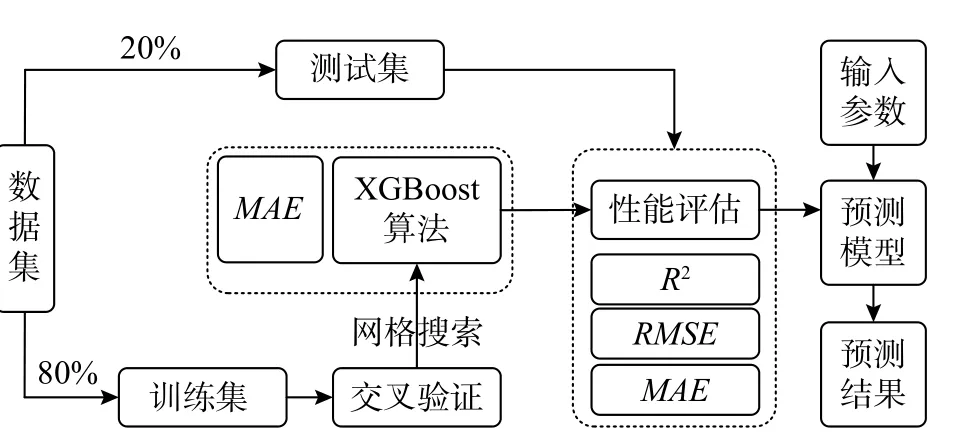
图3 基于XGBoost 的承载力预测模型建立流程Fig. 3 Flowchart of developing a XGBoost-based bearing capacity prediction model

步骤1. 数据集划分。按照8∶2 比例将数据集划分为训练集和测试集，得到的训练集包括122组数据，测试集包括31 组数据。

步骤2. 模型训练。基于训练集对XGBoost 进行训练，应用交叉验证和网格搜索策略进行超参数优化，训练以平均绝对误差MAE(mean absolute error)为优化目标，最终得到全局最优超参数组合下的预测模型。其中，交叉验证是在训练集上进一步划分出训练集和验证集，多次循环替换训练集训练模型，根据多次结果的预测精度均值评估模型预测效果，减小由于样本随机抽取导致的偏差影响；网络搜索使用穷举法将各超参数取值进行组合，训练选取表现最优的超参数组合，以避免选择的参数组合为局部最优组合。

步骤3. 性能评估。基于测试集对步骤2 得到的模型进行检验，模型预测精度通过拟合优度R2、均方根误差RMSE(root mean squared error)以及平均绝对误差MAE等指标进行量化衡量。

拟合优度R2代表回归结果对实测值的拟合程度，越接近于1 则代表回归结果的拟合程度越好。计算式如下：

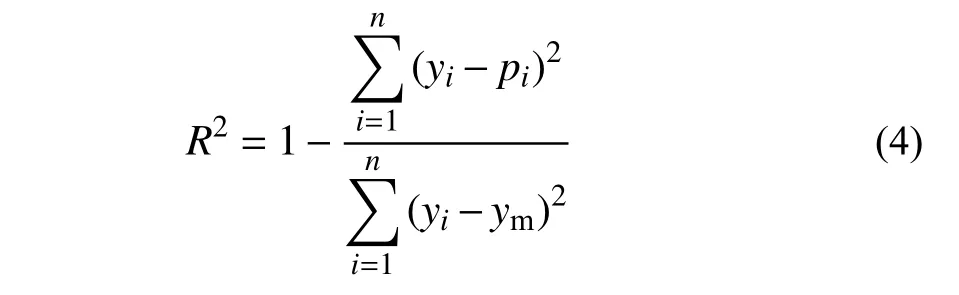
均方根误差RMSE反映预测值与实测值差异程度的度量，越小则模型精度越高，计算式如下：

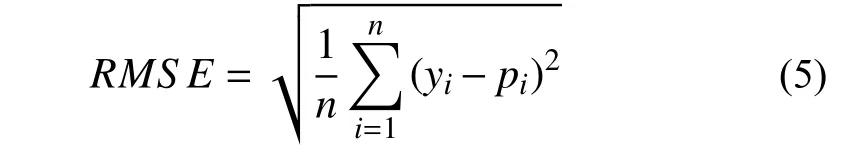
平均绝对误差是预测值与实测值间绝对误差的平均值，反映预测值误差的实际情况，越小则模型精度越高，计算式如下：

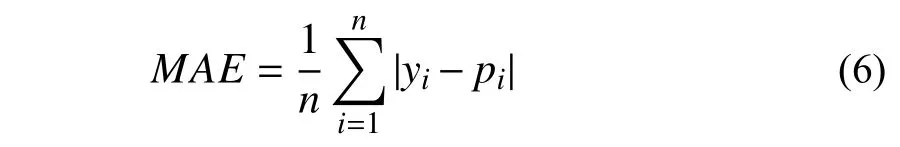
以上各式中：ym为样本均值；n为样本数量。

通过上述流程得到可用于FRP 加固RC 梁抗弯承载力预测的XGBoost 模型，使用时提供8 项输入参数，模型即可预测加固后梁承载力。

训练得到基于XGBoost 的FRP 加固RC 梁抗弯承载力预测模型超参数组合如表2 所示。

表2 XGBoost 参数Table 2 Parameters of XGBoost

3.2 对比模型建立

为对比基于XGBoost 的承载力预测模型精度表现，这里选用机器学习代表性算法SVR 和ANN通过相同的数据集建立起抗弯承载力预测模型。

SVR 通过核函数将低维数据非线性映射到高维特征空间，然后在高维特征空间内求取回归函数。使用同样的网格搜索法和交叉验证策略优化SVR 中超参数：惩罚系数C和核函数参数γ，优化过程如图4(a)所示。最终选定超参数C=1000，γ=0.1。

ANN 包括输入层、隐藏层和输出层三部分，每层神经元可以接收到前一层所有神经元的信号，并产生信号输出到下一层，信号从输入层到输出层做单向传播，整个网络中间无反馈。设置一层隐藏层，同样使用网格搜索法和交叉验证策略优化隐藏层神经元个数n和初始学习率α，图4(b)为参数优化过程，最终选定超参数n=400，α=0.15。

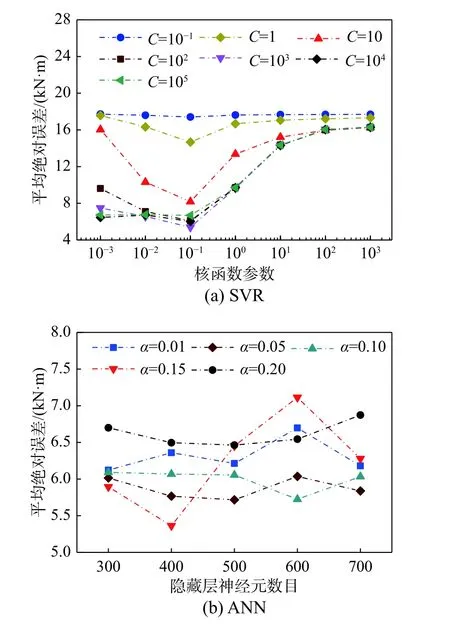
图4 网格搜索中SVR 和ANN 算法的验证结果Fig. 4 Validation results of SVR and ANN under grid search

3.3 结果讨论

图5 为三种模型的预测值与实测值对比结果。从中可以直观地看出，相比于SVR 和ANN，基于XGBoost 的抗弯承载力预测值更为集中的落在±10%的误差限内，落在±20%范围内的比例也明显更高。可见，基于XGBoost 算法的FRP 加固梁抗弯承载力预测模型对样本的预测效果最好。

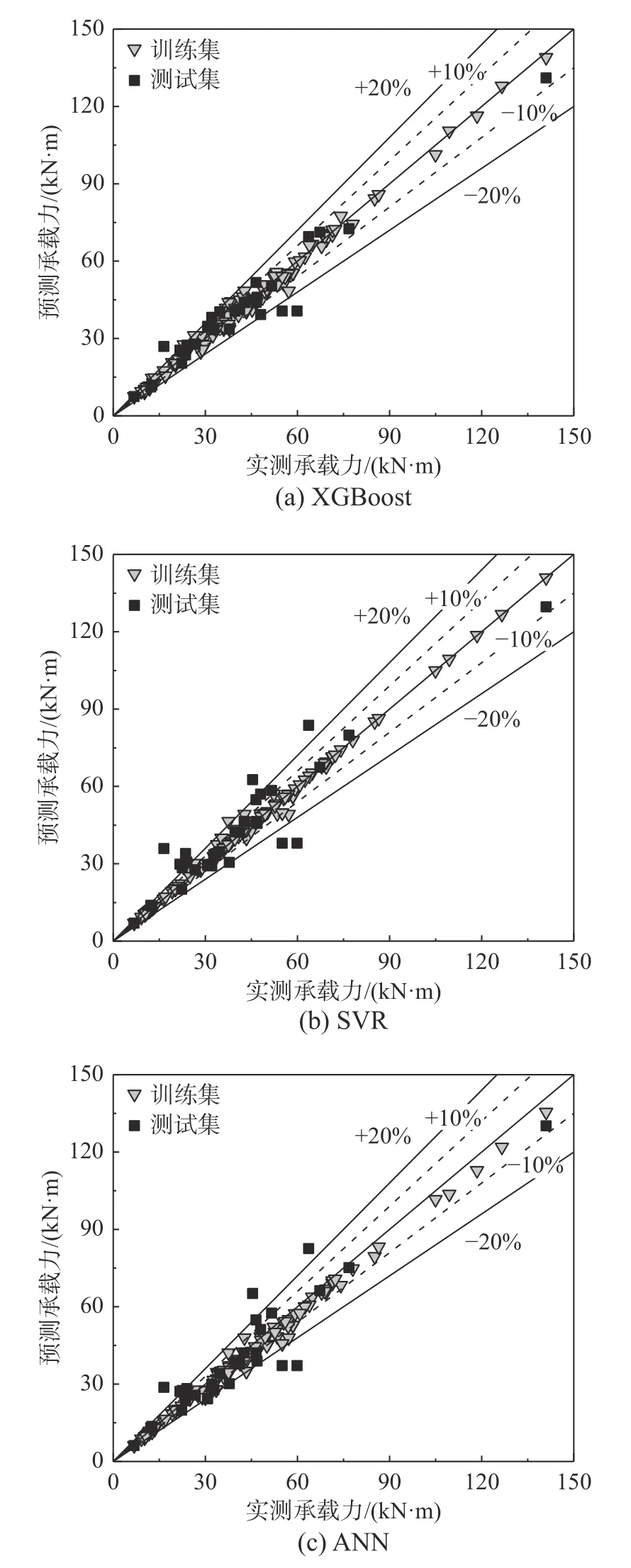
图5 不同模型拟合结果Fig. 5 Fitted result graphs of different models

表3 列出了三种模型在R2、RMSE以及MAE上对比结果。从表中可以进一步看到，基于XGBoost算法的R2达到0.9417，明显高于SVR 的0.8664和ANN 的0.8786，分别提升了8.00%及6.70%，对样本的拟合程度最好。同时，相比于SVR 和ANN，XGBoost 的RMSE分别降低了33.94%和30.72 %，MAE分别降低了32.38%和30.51%，可见XGBoost 的预测值与实测值差异最小，预测精度明显优于SVR 和ANN。

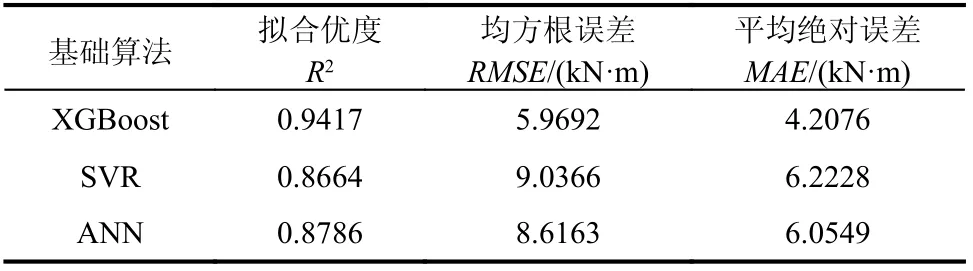
表3 不同模型评估指标Table 3 Evaluation of different models

图6 展示了三种加固方式下基于XGBoost 的承载力预测模型的预测值与实测值对比结果。从图中可以直观的看到，外贴式、端锚式和嵌入式三种情况下大部分预测值均落入±10%的误差限内，对于外贴式和端锚式加固，少量超出10%的预测值也均落入±20%误差限内，嵌入式情况下，绝大多数超出10%的预测值也落入±20%的误差限内，可见预测模型在外贴式、端锚式和嵌入式三种FRP 加固方式上均表现出较高精度。

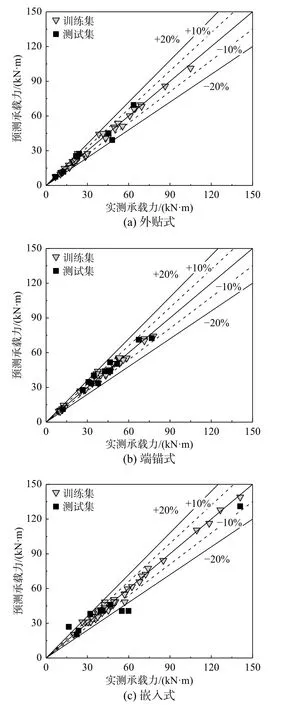
图6 不同加固方式拟合结果Fig. 6 Fitted result graphs of different strengthening methods

表4 列出了三种加固方式下基于XGBoost 的承载力预测模型在R2、RMSE以及MAE上的对比结果。表中可以进一步看到，外贴式、端锚式和嵌入式加固的R2分别达到0.9472、0.9631 和0.9278，对样本拟合均较为良好。在RMSE和MAE指标上，端锚式误差最小，其次为外贴式，嵌入式最弱。整体而言，三种加固方式抗弯承载力预测效果均较为良好，其中，外贴式和端锚式的预测效果最为优良，嵌入式稍弱。

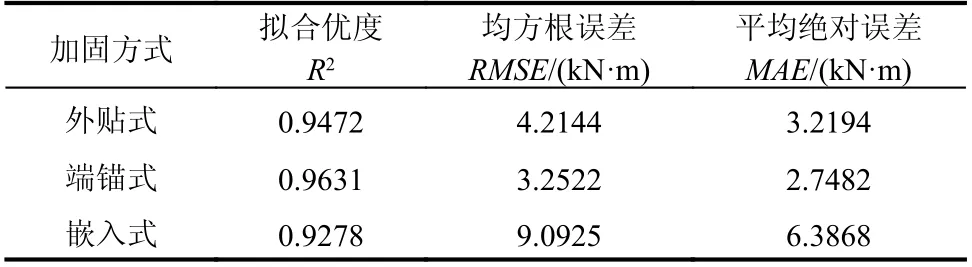
表4 不同加固方式评估指标Table 4 Evaluation of different strengthening methods

3.4 特征重要性分析

为证明基于XGBoost 的FRP 加固RC 梁抗弯承载力预测模型的合理性，本节使用Permutation Importance(排列重要性)进行特征重要性分析。

在针对某一输入特征进行重要性计算时，先将该列特征取值随机打乱并输入到预测模型中，得到新的预测输出。随后通过计算新的预测值与原预测值间的差值得到该参数的重要性。通过循环打乱各输入参数，即可得到所有参数的特征重要性。

图7 即为据此得到的8 个输入参数的特征重要性。可以看出，各参数的特征重要性均有一定程度的波动，但重要性排序稳定。其中梁高、梁宽和纵向钢筋配筋率对抗弯承载力影响最大。相比之下，FRP 材料配布率、钢筋屈服强度、混凝土立方体抗压强度、FRP 材料抗拉强度及弹性模量的特征重要性值较小。可见FRP 各加固参数并不是RC 梁承载力的决定性的因素，该现象是合理的。因为FRP 加固的作用只是在钢筋混凝土梁原有承载力的基础上提升承载力，起决定性作用的仍是初始梁的参数[51,70]。此外，三个FRP 相关参数中，配布率是影响加固效果的最重要因素，FRP 抗拉强度和FRP 弹性模量影响程度均小于配布率，二者大致相等，这也与相关FRP 加固混凝土梁试验结果相吻合[9,63]。

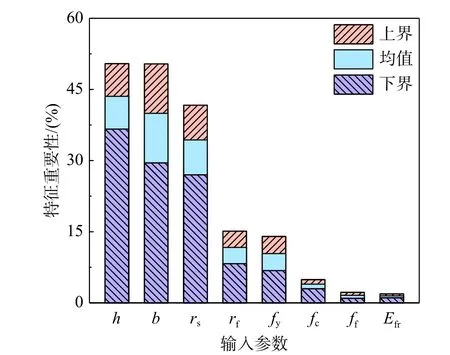
图7 基于XGBoost 的预测模型中参数的特征重要性Fig. 7 Feature importance of the parameters in the XGBoost based prediction model

4 结论

本文建立了基于集成学习XGBoost 算法的FRP 加固钢筋混凝土梁抗弯承载力预测模型，与基于SVR 和ANN 的模型进行精度对比，对不同加固方式下的预测精度进行了分析，并对模型进行了特征重要性分析，得出以下结论：

(1)基于XGBoost 的承载力预测模型展现出了较高的预测精度。在基于既有试验数据建立的测试样本集上，该模型的拟合优度达到0.9417。

(2)基于集成学习算法XGBoost 的承载力预测模型精度远优于基于传统机器学习算法SVR 和ANN 的预测模型。与基于SVR 和ANN 的模型相比，基于XGBoost 的模型拟合优度分别提升了8.00%及6.70%，均方根误差分别降低了33.94%和30.72%，平均绝对误差分别降低了32.38%和30.51%，可见性能提升明显。

(3)基于XGBoost 的承载力预测模型可以统一三种加固方式下的承载力预测模型。该模型在外贴式、端锚式和嵌入式加固方式下拟合优度分别达到0.9472、0.9631 和0.9278，精度表现接近，均较为优良。

(4)在说明预测模型的准确性后，通过特征重要性分析，证明了该模型的合理性。其中梁高、梁宽和纵向钢筋配筋率对RC 梁的抗弯承载力影响最大。三个FRP 加固相关参数中，配布率对加固效果影响最大，FRP 抗拉强度和弹性模量影响程度均小于配布率，二者大致相等。

(5)该预测模型具有相当的泛化能力，可以用于FRP 加固RC 梁的承载力预测，后续研究可以通过扩充数据集不断提升模型精度，并进一步在实际工程中进行验证，从而向桥梁维养决策提供参考。