基于离散宏单元的砌体结构高效非线性分析方法

郭 勇，余丁浩，李 钢

(大连理工大学海岸和近海工程国家重点实验室，辽宁，大连 116024)

砌体结构因其造价低廉、施工方便、性能优异而广泛存在于工业与民用建筑中，此类结构的主要材料为块体和砂浆组成的非均质复合材料，其力学行为由块体、砂浆和二者之间粘结界面的力学性能共同确定。块体和砂浆为典型的脆性材料，抗拉强度远小于抗压强度。二者之间粘结界面的力学性能差，界面受拉行为与材料粘性属性有关，界面剪切行为同时与材料粘性和摩擦属性有关。在极端环境荷载作用下，砌体结构将表现出显著的非线性特征。

目前，砌体结构非线性分析模型按照建模方式的不同可分为分离式和整体式两种。分离式模型将砂浆、块体及二者粘结界面分开建模，各部分的材料性质通过描述各自力学性能的本构关系表征，模型精细化程度高，但计算代价大。Lourenço和Rots[1]在块体-砂浆粘结界面模型中采用复合屈服准则考虑砌体墙的拉、压、剪非线性行为，并在非线性行为中考虑了材料的塑性软化特征；Sandoval 等[2]利用该模型完成了多孔黏土砖砌体墙和灌浆配筋砌体墙[3]的精细化数值模拟，与试验结果的对比分析结果显示该模型能够反映砌体的真实破坏形态； Lourenço[4]和Roca 等[5]对砌体结构非线性分析的数值计算问题进行了综述，认为分离式模型最突出的问题在于计算代价高昂，严重地限制了其在大型工程结构中的应用；Minga等[6]针对分离式模型应用于大型砌体结构计算代价高昂的缺点，采取将结构分解为若干部分，分配给不同处理器并行计算的方式进行非线性分析。整体式分析模型将块体和砂浆假定为连续的匀质体，建模过程简单，非线性分析所需计算量小，此类模型属于宏观分析模型，可以较好地平衡结构分析的计算效率和精度，其关键在于建立能够合理反映结构实际震害特点和关键失效模式的简化建模策略，当前已有众多学者开展了此方面研究，并提出了多种整体式分析模型，如匀质化模型[7-9]、等效框架模型[10-18]等，Grande 等[19]在梁单元的端部设置剪切界面，提出了可考虑砌体墙肢剪切失效的梁单元模型，将所提模型与节点区刚性单元联合使用模拟砌体墙的弯曲和剪切非线性行为；Addessi 等以Timoshenko 梁理论为基础，分别在分布式非线性梁单元模型[20]和集中非线性梁单元模型[21]中设置塑性剪切铰，并用该塑性铰模拟墙肢的剪切失效机制；Caliò等[22]提出了一种考虑砌体墙面内主要失效模式的平面离散宏单元模型，该模型用非线性弹簧构造剪切单元和无厚界面单元，通过耦合两种单元的变形模拟砌体墙的弯曲和剪切非线性行为，目前，该模型经不断改进被应用于无筋砌体墙在静力作用下[23]和动力作用下[24]的平面外受力特性分析、填充墙钢筋混凝土框架结构的平面内抗震分析[25-26]和平面外抗震分析[27-28]、无筋砌体结构的地震易损性分析[29]等，研究结果均表明该模型具有良好的分析精度和计算效率。综上所述，精细化的分离式模型适用于结构构件的细部分析和模拟，而整体式模型在大型砌体结构的分析和模拟方面具有更大优势。

无论整体模型或分离模型，通常采用传统变刚度法进行非线性求解，不可避免地需对切线刚度矩阵进行实时更新和分解，这导致随问题规模增大计算效率急剧降低。为了避免结构大规模整体切线刚度矩阵的实时更新和分解，国内外学者利用土木工程结构材料非线性的局部化特征，发展出一系列高效数值分析方法，例如多尺度方法、子结构方法、重分析方法等。其中，多尺度有限元法通过构造多尺度基函数，将局部非线性区域的精细化模型与其余部位的宏观模型进行有效耦合，避免了传统有限元法采用单一小尺度建模，大幅缩减结构自由度，Drosopoulos 和Stavroulakis[30]、 Giambanco 等[31]、 Silva 等[32]和Krejci 等[33]采用多尺度方法对砌体结构进行了非线性分析，分析结果证明该方法计算效率明显优于传统单一尺度建模方法。Clough 和Wilson[34]提出子结构方法，该方法依据边界力和变形协调条件将整体结构划分为线弹性子结构和非线性子结构，并通过静力凝聚的方式消去线弹性子结构的内部自由度，大幅降低结构自由度数目，提高了计算效率，但该方法需要预判非线性子结构的划分区域，且弹、塑性子结构一旦划分就无法改变，因而适用性有限。为克服其局限性，孙宝印和古泉等[35-36]对整体结构的单元弹塑性状态进行实时判断，仅将进入非线性状态的构件作为隔离塑性子结构，使大规模的非线性分析问题转化为整体结构的线弹性分析和规模较小的局部隔离子结构的非线性分析。重分析方法是一类利用初始结构计算信息快速求解修改后结构响应的计算方法，能够避免结构局部修改后进行耗时的完全分析，此类方法最初用于结构设计，随后被众多学者用来提升局部材料非线性分析的计算效率。重分析方法主要包含直接法和近似法，直接重分析法[37]将局部结构修改或局部非线性变形产生的刚度矩阵表示为初始弹性刚度矩阵的低秩修正形式，并基于Shearman-Morrison-Woodbury 公式进行问题求解，避免了整体切线刚度矩阵耗时的实时更新和分解，组合近似法[38]是基于预处理共轭梯度法发展而来的一种高效的近似重分析方法，该方法通过对变化的刚度矩阵进行降阶处理来缩减问题的计算规模，可快速求解大范围非线性结构的响应。拟力法[39-41]将构件的变形分为弹性和塑性两部分，可在控制方程中保持初始弹性刚度矩阵不变并通过仅更新小规模塑性刚度矩阵实现局部非线性问题的高效求解，受其概念启发，Li等[42-44]提出了隔离非线性法，该方法通过对非线性材料的应变进行分解，并与有限元理论结合，可将切线刚度矩阵转化为初始弹性刚度矩阵的低秩修正形式，结合Woodbury 公式实现了一般局部非线性有限元分析问题的高效求解，为克服该方法随非线性区域规模扩大时效率降低的不足，Li等[45-46]通过引入组合近似法的思想对该方法使用的Woodbury 求解公式进行了深度优化。上述学者针对结构局部非线性特征发展了多种高效数值分析方法，极大推动了结构分析领域的发展。

地震作用下砌体结构的非线性变形状态往往集中于楼梯间、纵横墙交接处等局部区域，具有典型的局部化特征，因此，利用其局部非线性特征发展适用的高效分析方法对提升计算效率具有积极意义。本文基于整体式空间离散宏单元模型，并充分利用结构局部非线性特征，提出了一种砌体结构高效非线性分析方法，首先建立剪切单元和无厚界面单元，并通过耦合两者之间的变形模拟砌体失效模式，随后，结合隔离非线性思想将剪切单元等效斜向弹簧的轴向变形和无厚界面单元上下表面的相对变形分解为线弹性和非线性两部分，并通过附加的塑性自由度描述其中的非线性部分，从而在控制方程中实现了线性与非线性刚度矩阵的分离，以该控制方程为基础将结构切线刚度矩阵表示为初始弹性刚度的低秩修正形式，最后，通过引入Woodbury 公式求解控制方程，使非线性分析过程的主要计算量集中于对一个小规模的非线性矩阵进行更新与分解，有效提升了非线性分析效率。数值模拟与试验结果的对比验证了本文方法的准确性，基于时间复杂度理论的计算效率分析结果表明该文方法在非线性分析效率方面较传统变刚度法具有明显优势。

1 离散宏单元模型

Caliò等[22]基于整体式建模策略提出了砌体结构的空间离散宏单元模型，如图1 所示，其根据砌体墙窗洞构造将墙体离散成一系列剪切单元和无厚界面单元，剪切单元为由四个刚性板和两个对角斜向非线性弹簧构成的铰接四边形结构，无厚界面单元由一系列不同功能的非线性弹簧构成。不同剪切单元之间或剪切单元与支座之间通过无厚界面单元相互连接，砌体墙的平面内、外失效模式通过耦合剪切单元和无厚界面单元的变形进行模拟。

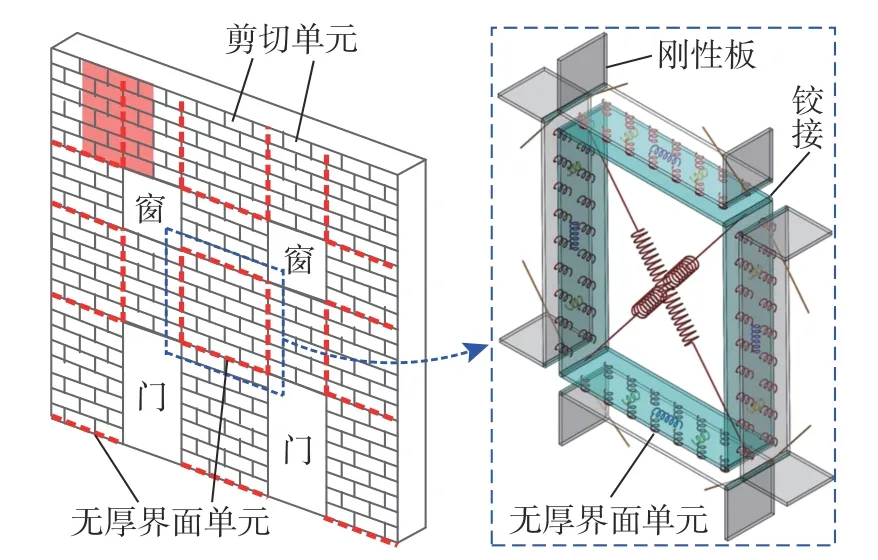
图1 空间离散宏单元模型Fig. 1 Spatial discrete macro-element model

砌体墙斜截面剪切破坏是受损砌体结构中最普遍的失效模式，当墙体在竖向荷载和水平地震作用下产生的主拉应力超过墙体的抗拉强度时，平行于地震作用方向的墙体产生斜向裂缝，如图2(a)所示。该破坏模式通过剪切单元进行模拟，剪切单元将墙肢等效为发生纯剪变形的均质板，非线性行为通过两个对角斜向非线性弹簧进行描述，如图3(a)所示。弹簧的初始弹性刚度可基于墙肢与均质板线弹性变形范围内的能量等效[22]确定，屈服强度可根据Turnsek-Cacovic 准则[22]确定，如图4(a)所示为斜向弹簧的单轴滞回模型[22,24]，模型中考虑了材料屈服软化和卸载刚度退化等非线性行为，卸载刚度退化系数可取为β=0.8[24]。

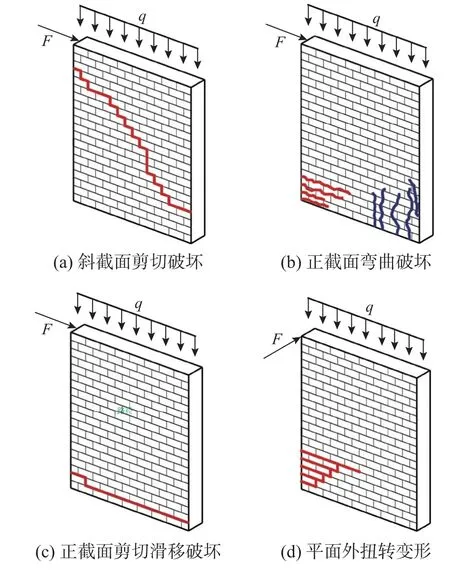
图2 砌体墙平面内外主要失效模式Fig. 2 Main in-plane and out-of-plane failure mechanisms of a masonry portion

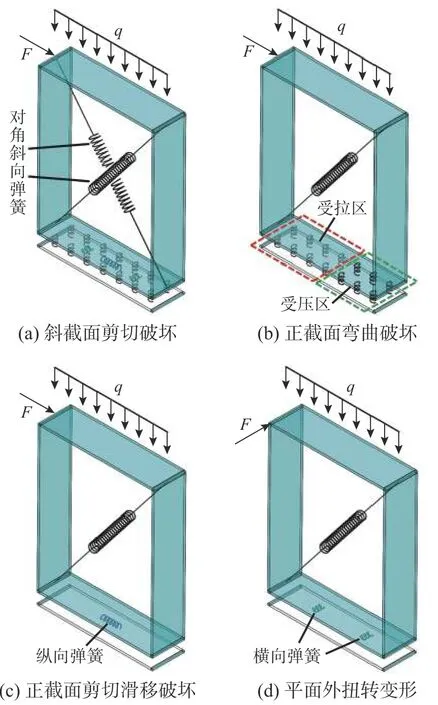
图3 离散宏单元模型模拟砌体墙平面内外主要失效模式(为简化说明，图(b)、(c)、(d)仅画出一根斜向弹簧)Fig. 3 Simulation of the main in-plane and out-of-plane failure mechanisms of a masonry portion by means of the macro-element (For simplicity, only one diagonal spring is shown in figures (b), (c) and (d))

砌体墙正截面弯曲破坏模式表现为墙体受拉区的开裂和受压区的压碎，如图2(b)所示。该破坏模式通过在墙肢截面处划分的若干匀质弹塑性纤维模拟，纤维的受力状态通过界面单元中m行n列法向非线性弹簧进行描述(图3(b))，在多个剪切单元与界面单元组合而成的砌体墙模型中，这些界面弹簧仅影响与其相连的剪切单元的一半区域(如图1 所示，墙体左上竖向界面单元仅影响单元左右两侧阴影区域)，图4(b)为这些弹簧的单轴滞回模型[22,24]，模型中考虑了材料卸载刚度退化行为，卸载刚度退化系数取为 β=0.8[24]。

当砌体墙竖向荷载较小或砌体与砂浆界面摩擦系数较低时，墙体易发生正截面剪切滑移破坏，表现为沿砌体的灰缝出现贯通截面的滑动摩擦行为，如图2(c)所示。为此，沿界面单元纵向设置一根剪切非线性弹簧描述墙体的正截面剪切滑移破坏，如图3(c)所示，该剪切弹簧的本构关系采用理想刚塑性模型[23-24](本文数值计算时将图4(c)所示理想弹塑性模型的弹性刚度取为大数)，屈服强度根据Mohr-Coulomb 准则[22]确定，模型中未考虑材料的卸载刚度退化行为，即 β=0。

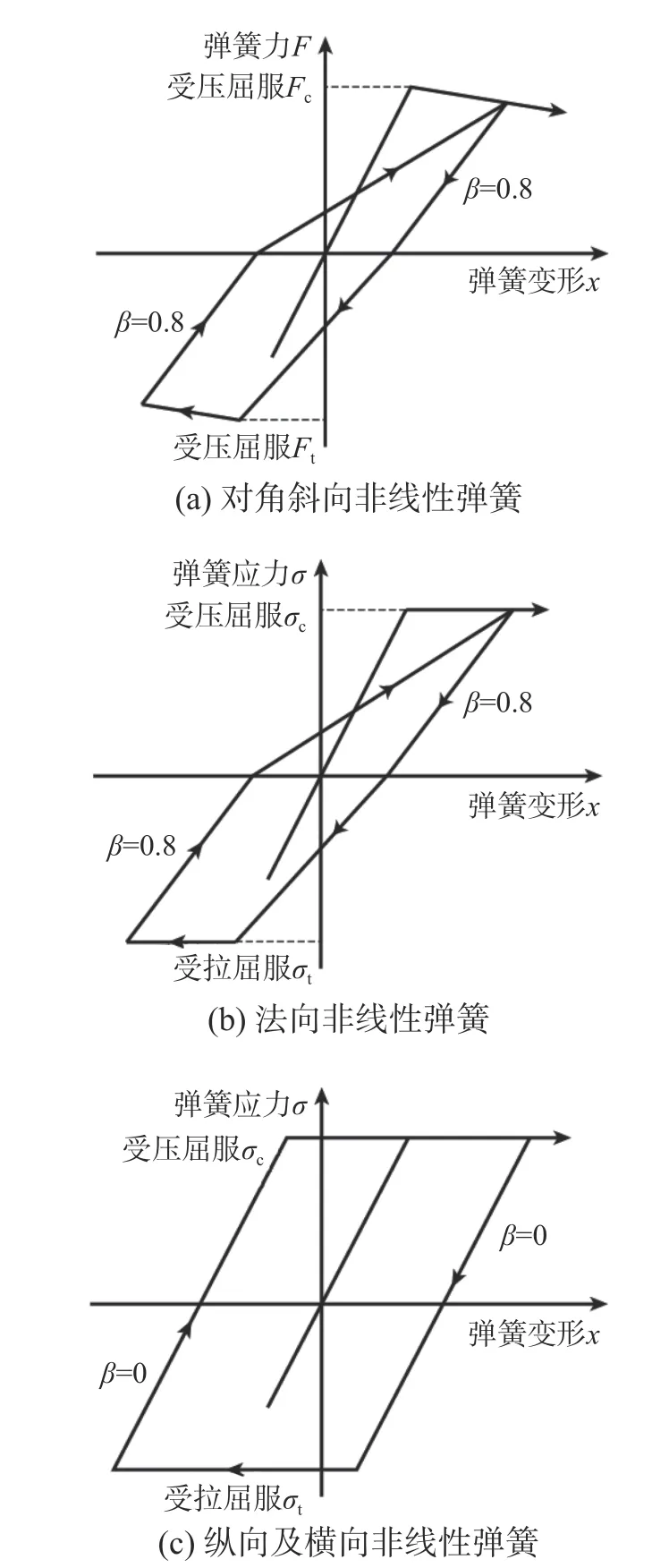
图4 砌体材料的单轴本构关系Fig. 4 Uniaxial constitutive laws of masonry material

当砌体结构纵、横墙间连接薄弱时，在沿横墙方向的水平地震作用下结构内外墙交接处易产生竖向裂缝，此时纵墙向外甩出发生平面外弯曲、剪切和扭转变形，此时墙体变形如图2(d)所示。模型中沿界面单元横向设置两根剪切非线性弹簧(图3(d))模拟墙体的平面外剪切、扭转变形，每根弹簧的单轴滞回模型如图4(c)所示，屈服强度根据Coulomb 失效准则确定[23-24]。

上述剪切单元通过无厚界面单元连接建立砌体墙片模型，如图1 所示，进一步将墙片模型通过共结点的方式连接，并根据结构楼盖形式及支承条件设定边界约束，即可建立整体结构分析模型，进而实现整体结构破坏形式和损伤演化过程的模拟。

2 非线性隔离宏单元模型

基于隔离非线性法基本思想，将材料应变或单元变形分解为线弹性和非线性两部分，图5 以单轴材料的非线性本构关系为例给出了应变分解的基本原理，假设在某个增量步内，材料的非线性状态由B点到C点，根据初始弹性模量Ee将材料应变增量分解为两部分：

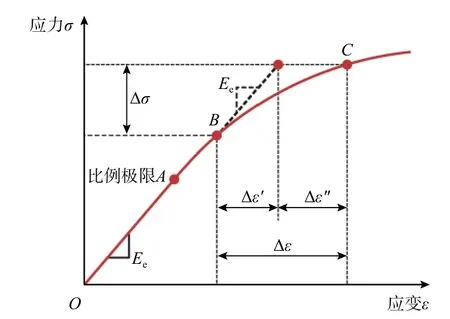
图5 非线性材料应变分解Fig. 5 Decomposition of nonlinear material strain

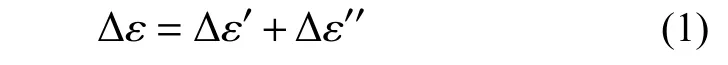
式中： Δε′为材料的线弹性应变增量； Δε′′为材料的非线性应变增量。与应变增量 Δε相对应的应力增量 Δσ可表示为：

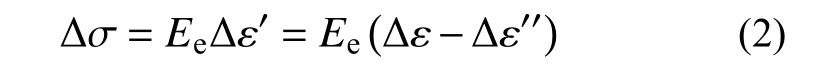
式(2)表明，无论何种本构模型，应变分解后任意时刻的材料应力均可表示为恒常的初始弹性模量与线弹性应变的乘积。

2.1 剪切单元模型

选择剪切单元的形心作为基本结点，每个基本结点k有7 个自由度，其中6 个为刚体运动自由度，1 个为剪切变形自由度，如图6 所示，其中oxyz为单元局部坐标系。在迭代过程的任一线性化增量步中，基本结点k位移增量向量可表示为：

如图6 所示，单元每个刚性板的中心设置1 个外部结点，共4 个外部结点。其中：①号、②号结点沿局部x轴布置；③号、④号结点沿局部z轴布置。每个外部结点r有6 个自由度，即有6 个广义位移和6 个广义力，其中仅在xz面内的剪力使单元发生剪切变形。外部结点r位移增量向量为：

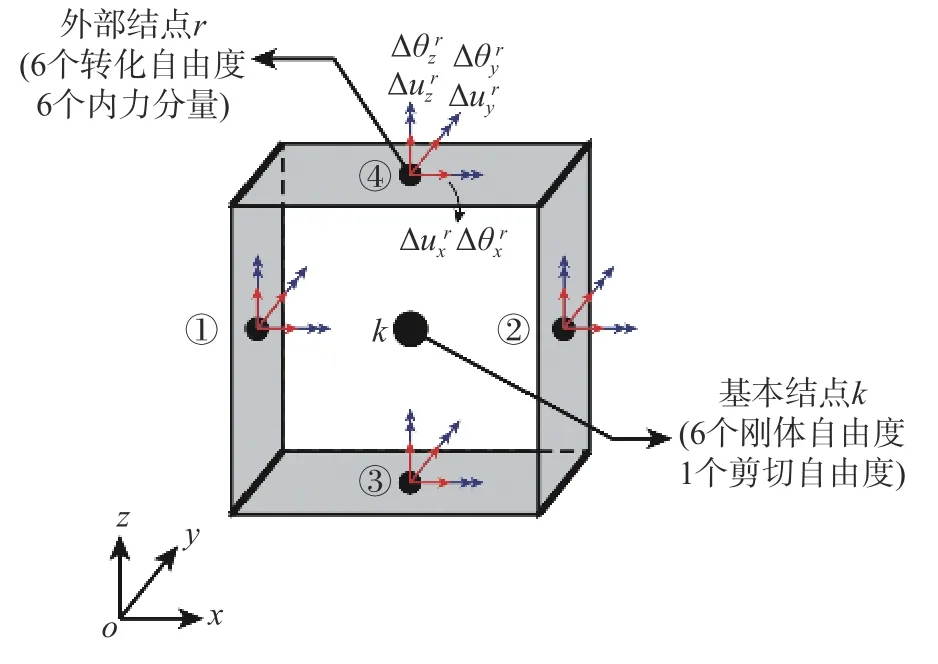
图6 剪切单元结点自由度Fig. 6 Shear element nodal degrees of freedom

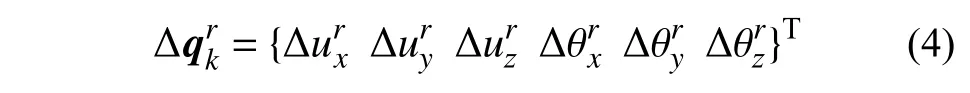
图7 给出了单元的剪切变形模式(考虑小变形假设)，将③、④号外部结点的连线定义为单元剪切变形模式的主线，该主线在xz面内的转动变形Δγy(基本结点剪切变形自由度)将引起主线端部外部结点③、④的平动位移dz·Δγy和其他外部结点①、②的转动位移 Δγy。

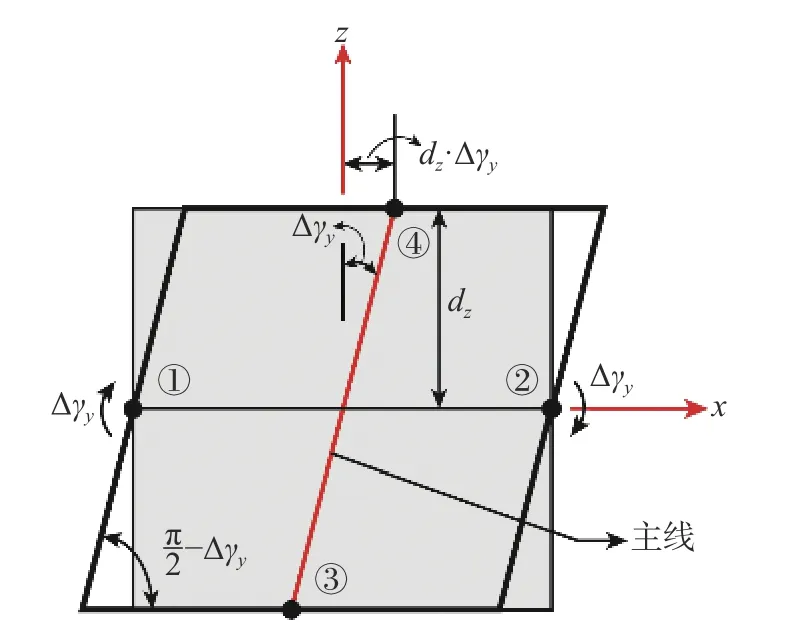
图7 剪切单元剪切变形模式Fig. 7 Shear deformation mode of shear element

在单元剪切变形模式下，等效斜向弹簧的变形如图8 所示，根据图中几何关系，可建立剪应变 Δ γy和弹簧变形 Δd之间的关系：

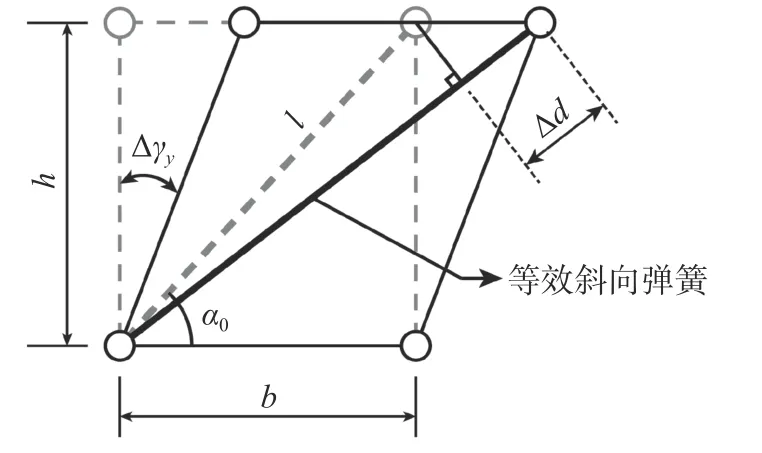
图8 等效斜向弹簧变形图Fig. 8 Deformation of equivalent diagonal spring

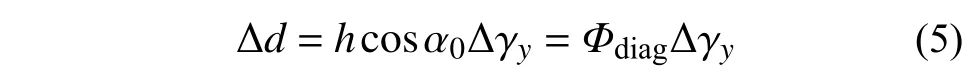
式中： Δd为剪切单元斜向弹簧变形增量； Φdiag为变形矩阵。

基于图5 所示的隔离非线性方法应变分解思想，可将等效斜向弹簧变形 Δd分解为线弹性和非线性两部分：

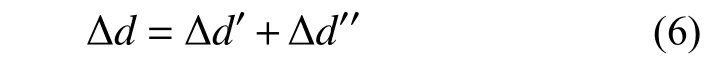
式中，线弹性部分 Δd′等于单元等效斜向弹簧初始弹性刚度的倒数乘以等效斜向弹簧内力增量ΔN，即：

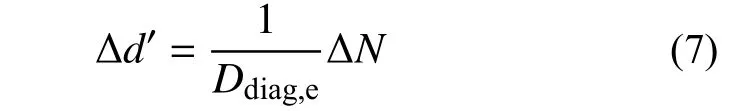
非线性部分 Δd′′等于弹簧变形增量 Δd与线弹性变形增量 Δd′的差值。斜向弹簧内力增量可表示为其初始弹性刚度与线弹性变形增量的乘积，即：

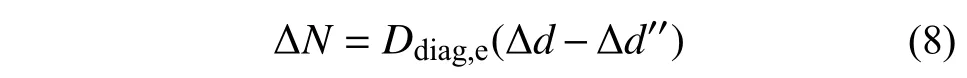
式中，Ddiag,e为剪切单元的等效斜向弹簧的初始弹性刚度。

2.2 无厚界面单元模型

基于多点线性约束方法(multi-point constraints,MPC)，剪切单元每一外部结点r的位移可以用基本结点k刚体运动引起的位移和剪切变形(图7 所示剪切变形模式)引起的转动位移或平动位移表示。在局部坐标系中，求解外部结点r的位移时，定义以基本结点k为起点、外部结点r为终点的向量=(dx,dy,dz)(如图9 给出了k=2，r=④2时的向量，④2表示基本结点2 的④号外部结点)，则单元外部结点r的位移函数为：

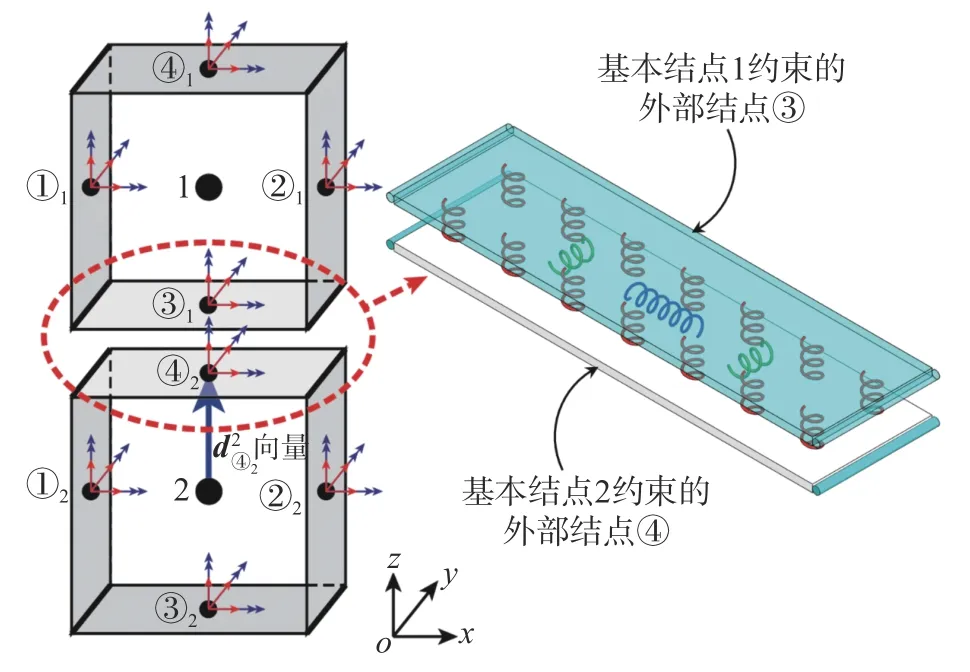
图9 无厚纤维界面单元Fig. 9 Zero-thickness fiber interface element

式中，等号右端第一项为基本结点k刚体运动引起的位移项，第二项和第三项分别为剪切变形引起的转动位移项和平动位移项，其中 Δγrot和Δγdisp分别为剪切变形模式下控制外部结点r转动位移和平动位移的转动自由度，erot=(,,)和edisp=(,,) 分 别为 Δγrot和 Δγdisp的单位方向向量，在图7 所示的单元剪切变形模式下，控制外部结点①、②位移的转动自由度 Δγrot=Δγy，Δγdisp=0，erot=(0,1,0)，控制外部结点③、④位移的转动自由度 Δγrot=0 ， Δγdisp=Δγy，edisp=(0,1,0)。

图9 表示出无厚纤维界面单元连接基本结点1 的③号外部结点(即图中③1结点)和基本结点2 的④号外部结点(即图中④2结点)。从图9 可知相邻③1、④2号外部结点的相对位移产生了界面相对变形，基于此可将界面单元相对位移函数表示为：

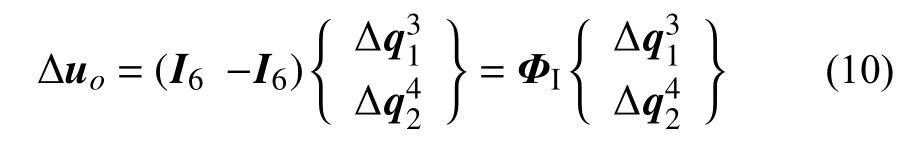
式中： Δuo={ΔuΔvΔwΔθxΔθyΔθz}T为界面单元相对变形增量；I6为6 阶单位矩阵； ΦI为变形矩阵。

将无厚界面单元的相对变形 Δuo分解为线弹性和非线性两部分：

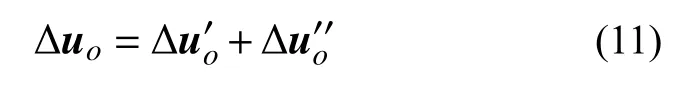
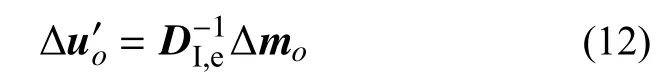
为方便后文对图3(b)、图3(c)、图3(d)描述的单元变形分量展开讨论，对界面单元相对变形增量进行初等变换后写为：

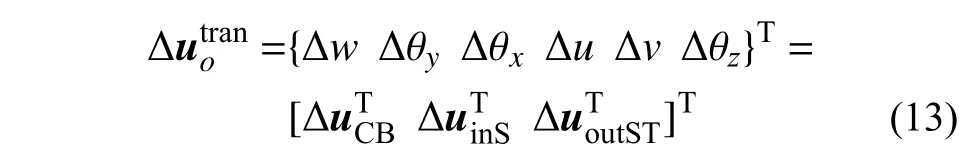
式中： ΔuCB={ΔwΔθyΔθx}T为单元法向弹簧模拟压弯受力行为的变量； ΔuinS={Δu}T为局部x向切向弹簧控制面内剪切滑移变形的变量；ΔuoutST={ΔvΔθz}T为局部y向切向弹簧模拟面外剪扭受力行为的变量。基于此可将分解后的界面单元变形写为如下形式：

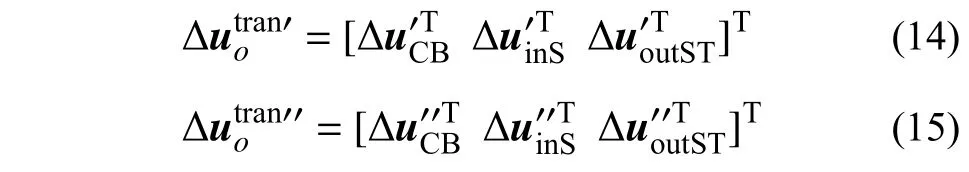
式(16)中，DCB需通过对单元中各法向弹簧的弹性刚度集成得到，即：

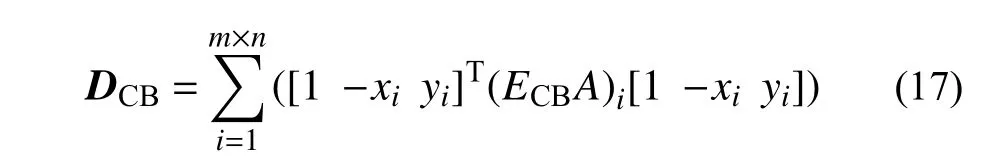
式中：ECB和A分别为弹簧的弹性模量和影响面积；xi和yi为第i根弹簧的局部坐标，弹簧沿局部y向布置m行，沿局部x向布置n列，m×n为弹簧的数量，DinS根据单元中沿局部x向切向弹簧的弹性刚度得到：

式中：EinS代表弹簧的弹性模量；沿单元局部x向设置一根切向弹簧，影响面积AinS为单元的面积；DoutST需对单元中沿局部y向两根弹簧的弹性刚度集成得到：

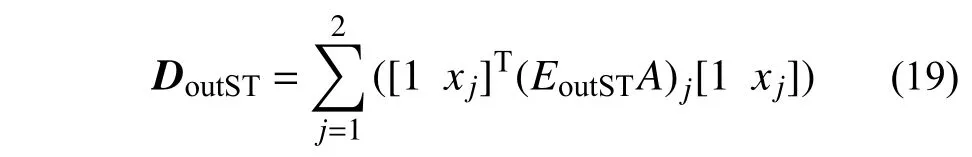
式中：EoutST和A分别为弹簧的弹性模量和影响面积；xj表示第j根弹簧的局部坐标。

1) 根据隔离非线性法中的变形分解原理，单元中第i根法向弹簧的相对位移增量可分解为：

实际分析中采用Newton-Raphson 迭代法求解，理想弹塑性模型会导致刚度矩阵奇异而出现求解失败，为了改善数值计算的收敛性，本文将本构关系中屈服后刚度与弹性刚度的比值取为0.001。当弹簧本构关系采用理想弹塑性模型时，根据图5 所示非线性区段内的材料应变分解思想，相应的弹簧应力增量可表示为：

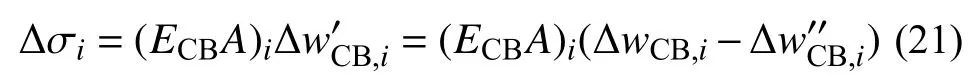
对单元中各法向弹簧的应力增量进行集成，可得与 ΔmCB对应的单元法向内力和弯矩表达式：

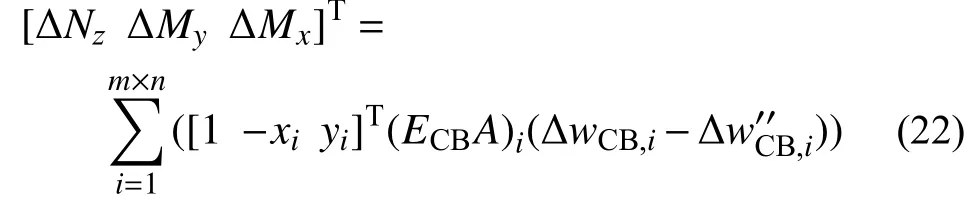
式中： ΔNz为单元法向内力； ΔMy和 ΔMx为单元弯矩。将式(22)代入式(16)中可建立与各法向弹簧的相对位移的关系：

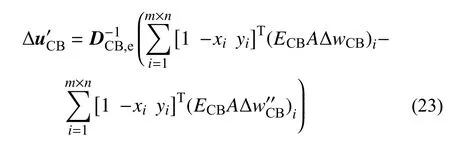
对比式(23)和式(12)可知，单元相对变形分量 ΔuCB和非线性相对变形分量可分别表示为：

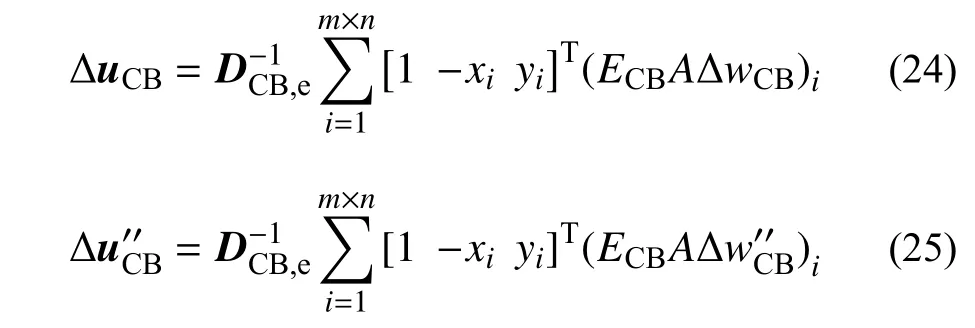
式(25)表明，当单元中所有法向弹簧的非线性相对位移均为零值时，单元的相对非线性变形分量才为零向量(此时相应塑性自由度处于未激活状态)，若部分弹簧的非线性相对位移为非零值，则无论这些弹簧数量的多寡，单元非线性相对变形分量均为非零向量(此时相应的塑性自由度被激活)。

2) 沿单元局部x向仅设置一根切向弹簧，与ΔminS对应的单元剪力为：

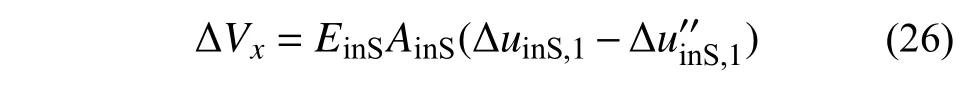
式中， ΔVx为单元剪力。根据单元线弹性变形表达式(12)可知当单元中该切向弹簧处于弹性状态时，单元非线性相对变形分量为零向量(相应塑性自由度未激活)，若为非零值，则为非零向量(相应塑性自由度被激活)。

3) 同样地，对单元中沿局部y向切向弹簧的剪切相对位移进行分解，将两根弹簧的应力增量进行集成，得与 ΔmoutST对应的单元剪力和扭矩为：[ΔVyΔMz]T=

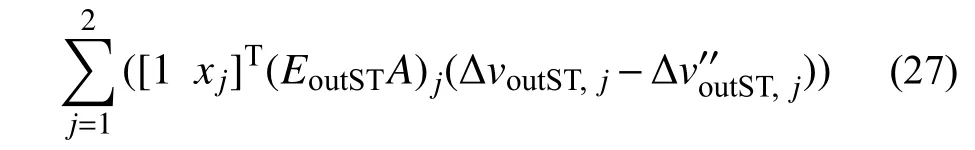
式中： ΔVy为单元剪力； ΔMz为单元扭矩。进一步根据单元线弹性变形表达式(12)可知单元相对变形分量 ΔuoutST和非线性相对变形分量分别为：

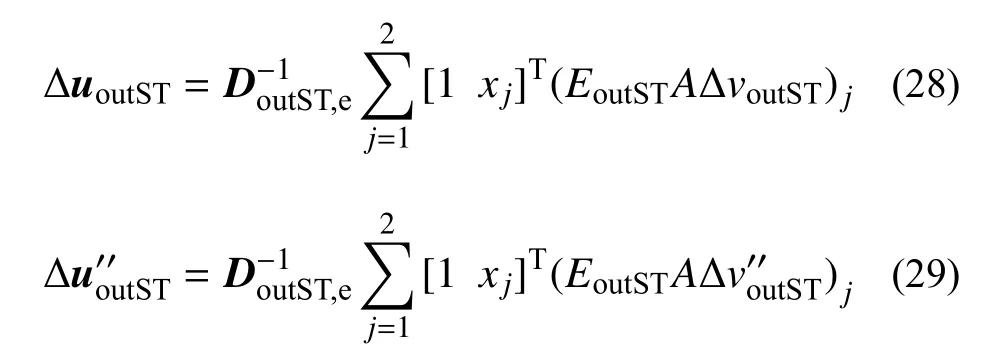
式(29)表明，当单元中两根切向弹簧的非线性剪切相对位移均为零值时，单元的非线性相对变形分量才为零向量(相应塑性自由度未激活)，若其中一根弹簧的非线性剪切相对位移为非零值，单元非线性相对变形分量为非零向量(相应塑性自由度被激活)。

2.3 单元控制方程

上述剪切单元和界面单元的变形分解后，单元内力增量与其变形增量和非线性变形增量相关，式(5)和式(9)、式(10)分别给出了剪切单元和界面单元变形增量的计算模型，单元非线性变形通过 Δd′′和进行描述，其中每个元素代表一个塑性自由度。

图9 建立的两基本结点单元可作为模型的基础单元，包含两个剪切子单元及一个界面子单元，建立其虚功方程如下：

式中： δu为单元的虚变形向量；ΔT=[ΔNT]T为单元内力； δa为单元虚结点位移向量； Δf为结点荷载增量。将单元位移函数式(5)、式(9) 、式(10)和内力增量表达式(8)、式(16)代入虚功方程式(30)，整理可得：

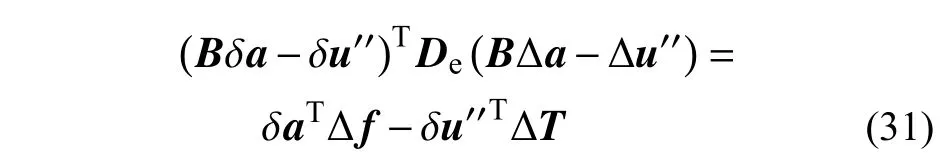
此外，考虑单元中各弹簧的非线性本构关系可建立补充方程，对于进入非线性状态的单元内力使用下式求解：

将式(32)代入式(31)，可得基础单元的隔离非线性控制方程：

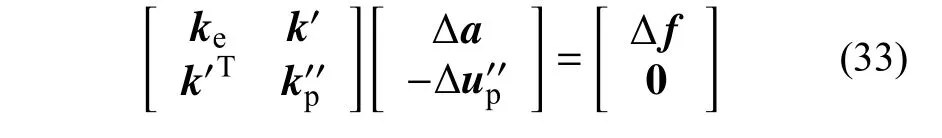
式中：ke为单元的初始弹性刚度矩阵；k′为描述单元结点力与非线性变形之间联系的系数矩阵；为描述单元非线性行为的系数矩阵。具体通过下式计算：

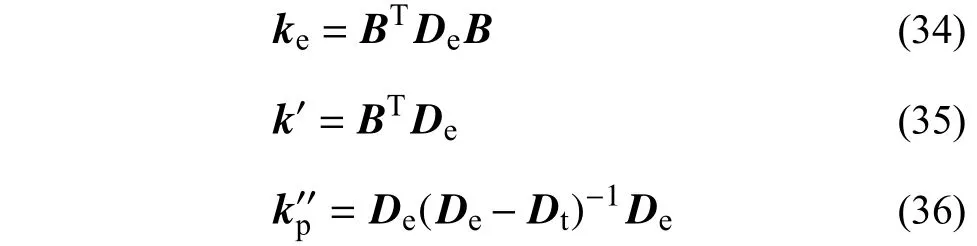
式中，B矩阵为代表基本结点自由度与两剪切子单元斜向弹簧变形 Δd和界面子单元相对变形 Δuo之间关系的变形矩阵。对B矩阵，可先将式(9)代入式(10)得到界面单元的变形矩阵，再将式(5)扩充为与其统一阶数的矩阵形式，最后进行合并得到。De=diag(DI,e,Ddiag,e)，且Ddiag,e=diag(,)，和分别为图9 中相邻1、2 号剪切单元的等效斜向弹簧的初始弹性刚度，Dt为相应的切向刚度矩阵。

3 结构控制方程求解

将基础单元控制方程进行集成，可得整体结构的隔离非线性控制方程：

式中： ΔX和 ΔF分别为整体结构的结点位移增量向量和结点荷载增量向量；为整体结构的非线性变形增量向量，其中仅包含了结构中呈激活状态的m个塑性自由度；Ke为整体结构的初始弹性刚度矩阵，其规模为n×n阶，阶数等于结构位移自由度数n；K′为描述整体结构结点力与非线性变形之间联系的系数矩阵，其规模为n×m阶；为描述整体结构材料非线性行为的系数矩阵，其规模为m×m阶。当结构发生局部材料非线性变形时，激活的塑性自由度数目m将远小于结构自由度数目n(即m＜＜n)。

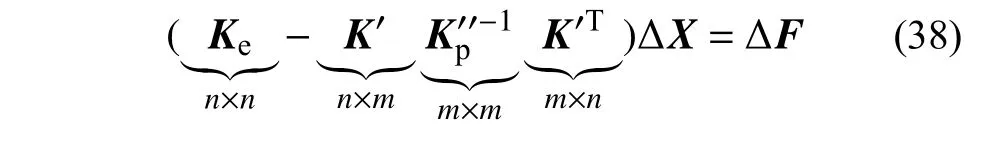
式(38)表明：当m远小于n时，任意时刻结构的切线刚度矩阵可表示为初始弹性刚度矩阵的低秩摄动形式。

采用完全Newton-Raphson 迭代法进行结构非线性分析，引入Woodbury 公式(式(39))在每个迭代步中对相应式(38)进行高效求解：

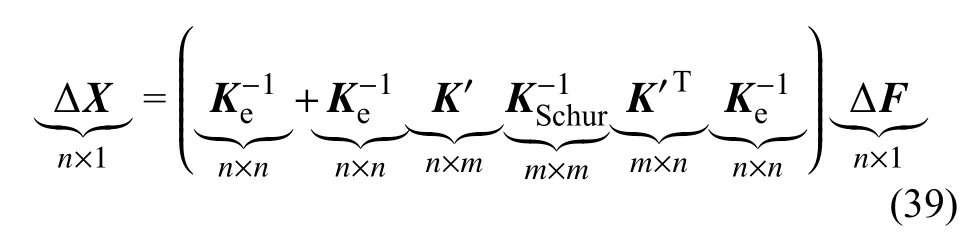
式中，KSchur为Schur 补矩阵：

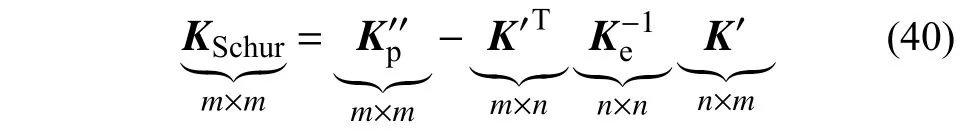
从式(39)可以看出，结构整体刚度项Ke在整体分析过程中始终保持初始弹性状态，仅需在分析前进行一次分解即可，当材料非线性集中在结构的局部区域时，控制方程中塑性自由度数目远小于结构自由度数目(即m＜＜n)，此时Woodbury公式在求解结构切向位移反应时的主要计算开销将仅集中于小规模的Schur 补矩阵(m×m阶)的更新分解[43]，从而可避免传统变刚度法中对整体切线刚度矩阵(n×n阶)的反复合成与分解运算，实现计算效率的大幅提升。

4 数值算例

4.1 试验验证

为了验证本文提出的砌体结构非线性分析方法的正确性，以Anthoine 等[47]的拟静力试验数据为依据，对2 片不同高度的砖砌体墙进行数值模拟。墙体的材料属性和几何属性分别如表1 和表2所示，2 片墙体在竖向压应力下的低周反复荷载试验结果如图10 所示，其中图10(a)为Wall-1 正截面弯曲破坏的试验滞回曲线，可以看出，曲线捏缩较为显著，墙体耗能能力较弱但强度在变形较大时没有明显退化；图10(b)为Wall-2 斜截面剪切破坏的试验滞回曲线，曲线的包围面积较大，墙体耗能能力相对较强，但存在严重的刚度和强度退化，试验详细信息见参考文献[47]。

表1 墙体材料属性Table 1 Material properties of masonry walls

表2 墙体几何属性Table 2 Geometry properties of masonry walls

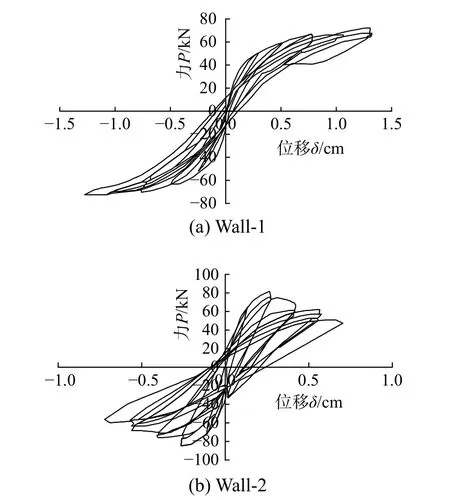
图10 砌体墙片试验滞回曲线Fig. 10 Experimental behaviour of simple piers

采用本文方法模拟2 片砌体墙在竖向荷载和水平荷载共同作用下的面内滞回行为，每个模型使用1 个剪切单元和1 个设置于底端的无厚界面单元。模型中各类非线性弹簧的力学参数取值根据表1 中砌体墙力学参数确定。两个模型数值模拟结果如图11 所示，分别为Wall-1 和Wall-2 基底剪力与顶点位移之间的滞回曲线，此外，图12给出了Caliò和Pantò等求解的Wall-1 和Wall-2 两片砌体墙宏单元模型在低周反复荷载作用下的滞回曲线(CP 方法求解结果)[22]。对比砌体墙数值模拟与试验结果：三者刚度和强度整体上吻合良好，其中CP 方法求解Wall-1 滞回曲线捏缩更为显著，这是由模型中非线性弹簧本构关系中滞回规则的差异所导致的。为更充分验证本文方法的正确性，图13 提取了三组滞回曲线的骨架曲线，从图中知，对比Wall-1 顶端最大位移处荷载P1，本文方法求解结果和CP 方法求解结果与试验结果的相对误差分别为12.38%和16.14%；对比Wall-2 顶端最大位移处荷载P2，本文方法求解结果和CP 方法求解结果与试验结果的相对误差分别为9.51%和25.73%。可见：本文方法求解误差小于CP 方法，本文所提方法可以有效地模拟砌体墙的失效模式，验证了该分析方法的正确性。

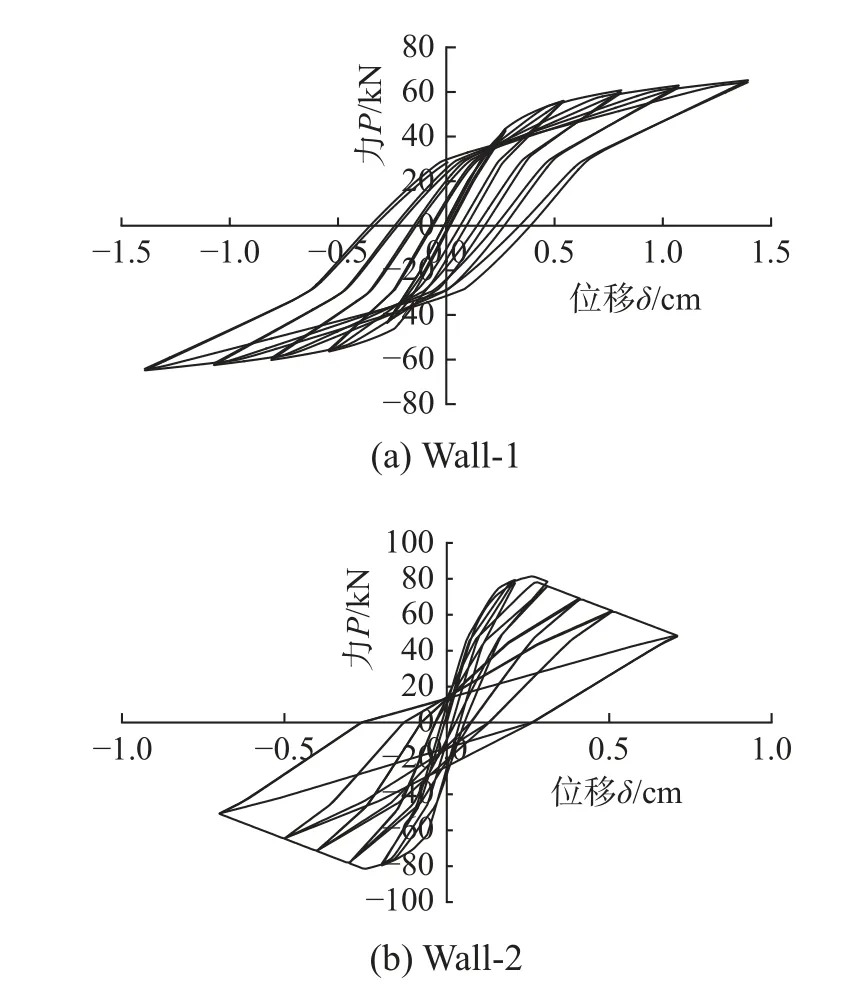
图11 砌体墙片本文方法计算滞回曲线Fig. 11 Numerical simulation results of piers(proposed method)

图12 砌体墙片CP 方法计算滞回曲线Fig. 12 Numerical simulation results of piers (CP method)

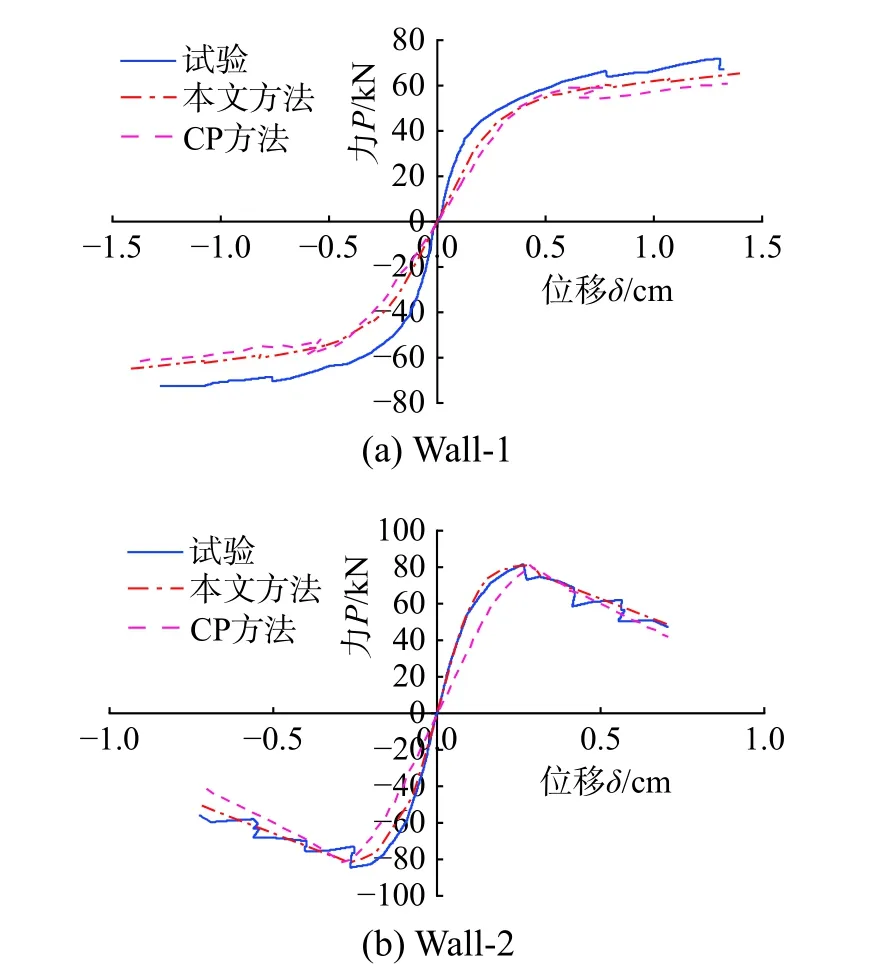
图13 砌体墙片骨架曲线Fig. 13 Skeleton curves of simple piers

4.2 动力非线性分析

为进一步对本文方法进行验证，对某4 层约束砌体结构进行地震反应分析，该结构平面简图如图14 所示。结构层高为3 m，总高度为12 m，纵墙上窗洞的尺寸为1.5 m ×1.8 m，门洞的尺寸为1.0 m ×1.8 m。在结构纵横墙交接处设置构造柱(如图14 所示)，结构所有纵横墙在楼层标高处设置钢筋混凝土圈梁，构造柱和圈梁采用C20 混凝土，截面尺寸为250 mm ×250 mm，纵筋采用4 根HRB335直径16 mm 的钢筋；墙体厚度为250 mm，材料为烧结普通砖，强度等级为MU10，混合砂浆强度等级为M10。结构楼面恒载为5.49 kN/m2，活载为2.0 kN/m2，屋面恒载为6.371 kN/m2。设防烈度为8 度(0.2g)，Ⅱ类场地，地震动选取汶川地震中卧龙波(幅值为400 cm/s2)，加速度时程如图15 所示。图16 为本文方法建立的该结构数值分析模型，其中，模型假设在结构首层底端设置固定约束，圈梁和构造柱采用隔离非线性纤维梁单元进行模拟，共划分1894 个隔离非线性纤维梁单元[48]，砌体墙划分为4198 个剪切单元和9770 个无厚界面单元，该空间模型共有39 934 个位移自由度。圈梁与构造柱和砌体墙的相互连接通过在接触面设置界面单元的方式实现，另外，在楼板的每一区格设置两根斜向刚性杆传递水平荷载和协调楼面结点位移。为简化模拟，本例中仅考虑纤维界面单元的轴向和弯曲非线性变形，其剪切和扭转变形假设为弹性。

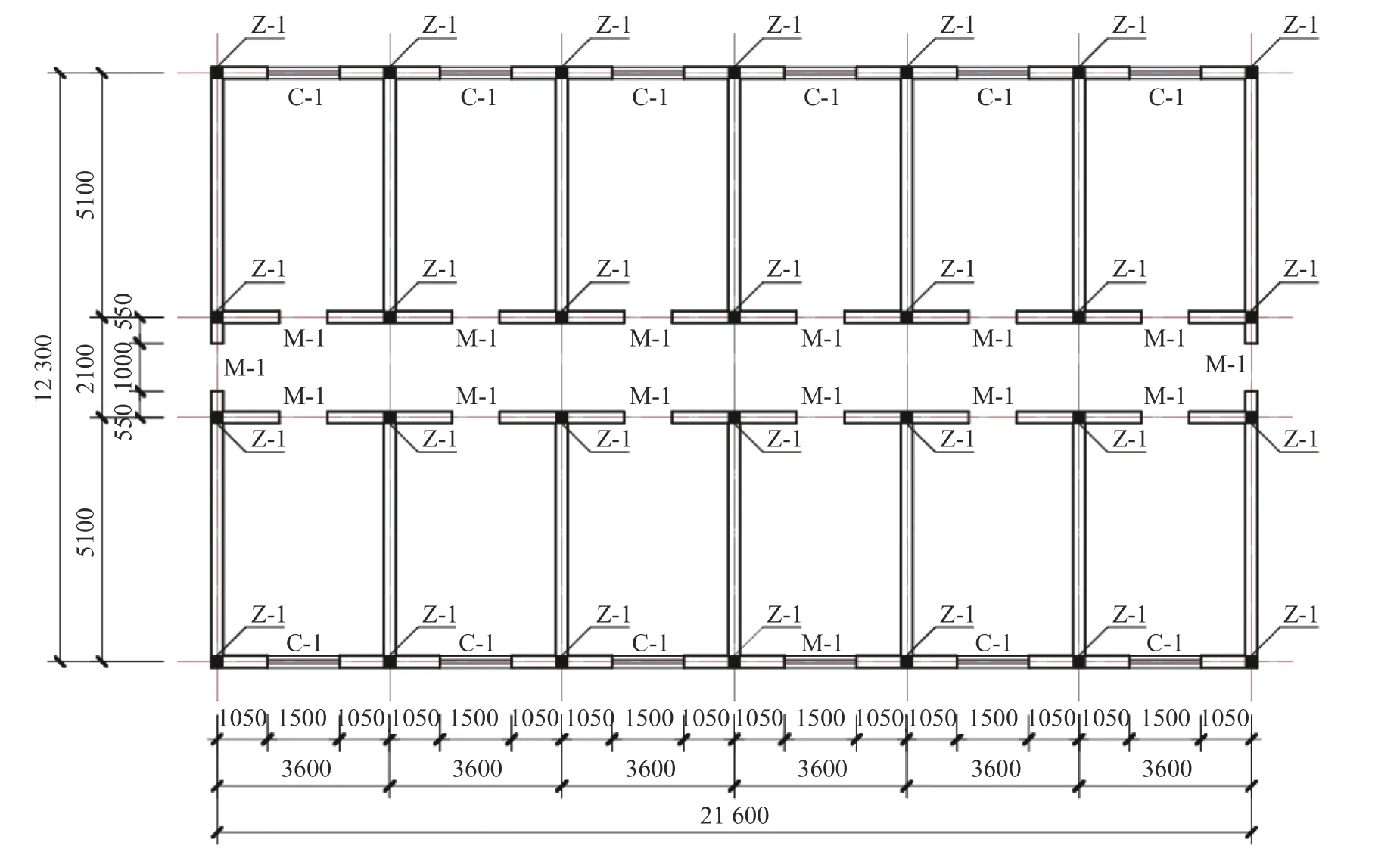
图14 结构平面简图Fig. 14 Plane of the masonry structure

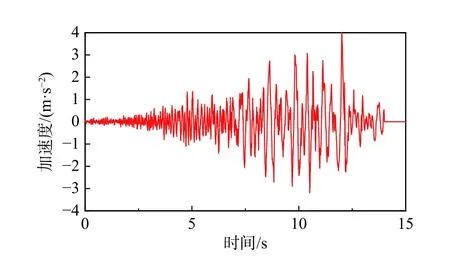
图15 卧龙地震波加速度记录Fig. 15 Acceleration record of Wolong earthquake

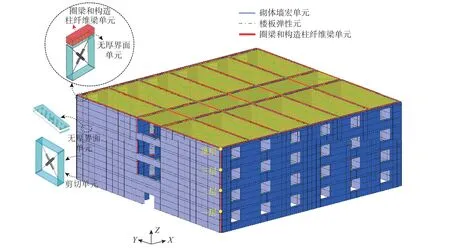
图16 约束砌体结构数值分析模型Fig. 16 Discrete macro-element model of the masonry structure

结构动力响应分析之前对结构进行模态分析，发现结构第一阵型是一阶Y向平动，一阶阵型的周期为T1=0.14 s，第二阵型是一阶X向平动，二阶阵型的周期是T2=0.1 s。分析结构在Y向水平地震作用下的动力响应，结构外纵墙与外横墙交接处各楼层(图16 示)位移时程响应如图17所示，结构的基底剪力时程响应如图18 所示，根据各楼层位移时程曲线发现该结构底层层间位移角最大，峰值达到0.6%，依据文献[49]中约束砌体结构0.4%的倒塌限值判定该砌体结构已达到倒塌的破坏状态。本砌体结构主要震害集中在底层，外横墙墙肢的损伤分布如图19 所示，墙体下部1 层、2 层的剪切单元均发生剪切破坏，下部损伤明显比上部严重。

图17 各楼层位移时程曲线Fig. 17 Time-history curves of all floors

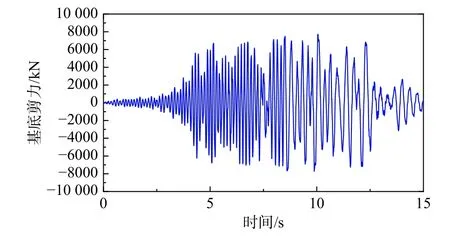
图18 结构基底剪力时程曲线Fig. 18 Base shear force curve of the masonry structure

图19 外横墙损伤分布图Fig. 19 Damage distribution of outer transversal wall

图20 给出了塑性自由度数随增量步的变化曲线，在3.265 s(增量步为653 步)之前结构处于弹性状态，塑性自由度数为0。非线性分析过程中产生的最大塑性自由度数为6545，占总自由度数的16.4%，而每个增量步的平均塑性自由度为1997，仅占总自由度数的5%，说明结构具有显著的局部非线性特征，采用式(39)进行求解时，由于需进行实时更新和分解的Schur 补矩阵阶数等于塑性自由度数目，局部非线性引发的较少的塑性自由度可保证本文方法实现大幅度的效率提升。

图20 塑性自由度时程曲线Fig. 20 Time-history curves of plastic degrees of freedom

为了进一步论证本文方法的高效性，将传统非线性分析方法(矩阵分解采用LDLT法)和本文方法的时间复杂度[50]进行统计对比，如图21 所示，传统非线性分析方法和本文方法的平均时间复杂度分别为1.54 ×1010和1.40 ×109，传统方法的平均时间复杂度是本文方法的11 倍，证明了本文方法的高效性。

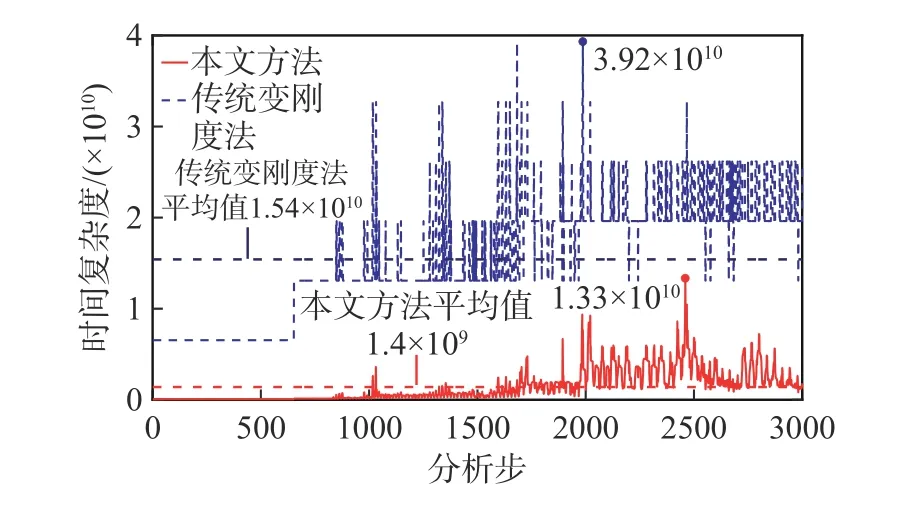
图21 时间复杂度时程曲线Fig. 21 Time-history curves of time complexity

5 结论

本文通过耦合剪切单元和无厚界面单元来模拟砌体结构失效行为，以隔离非线性法理论为基础，通过将剪切单元中等效斜向弹簧轴向变形和无厚界面单元上下表面的相对变形分解为线弹性和非线性两部分，推导出砌体结构离散宏单元的隔离非线性控制方程，采用Woodbury 公式求解控制方程，得到如下结论：

(1) 本文利用砌体结构材料非线性的局部化特征建立了结构非线性隔离宏单元模型，该模型基于多点线性约束方法使每个基本结点的自由度大幅缩减，相比于已有宏观模型和精细模型，其在大型砌体结构非线性分析时既能保证较高的计算精度也能使模型规模维持在相对较低的程度。同时，模型中激活的塑性自由度数目等于结构控制方程中小规模非线性矩阵的维度，其可直观地衡量砌体结构中产生增量非线性变形的区域规模。

(2) 通过分离结构弹塑性状态使砌体结构非线性分析时仅对小规模非线性矩阵进行更新和分解，可以避免传统变刚度法中对整体切向刚度矩阵的更新与分解，该方法的时间复杂度明显低于传统变刚度法，可以实现砌体结构非线性问题的高效求解。