Valley-dependent transport in strain engineering graphene heterojunctions

Fei Wan(万飞)， X R Wang(王新茹)， L H Liao(廖烈鸿)， J Y Zhang(张嘉颜)，M N Chen(陈梦南)， G H Zhou(周光辉)， Z B Siu(萧卓彬)，Mansoor B.A.Jalil， and Yuan Li(李源)，†

1Department of Physics，Hangzhou Dianzi University，Hangzhou 310018，China

2Department of Physics and Key Laboratory for Low-Dimensional Quantum Structures and Manipulation(Ministry of Education)，Hunan Normal University，Changsha 410081，China

3Computational Nanoelectronics and Nano-device Laboratory，Electrical and Computer Engineering Department，National University of Singapore，Singapore 117576，Singapore

Keywords: strain engineering，valley-dependent separation，graphene，on-site energy

1. Introduction

So far，extensive attention[1，2]has been given to graphene systems owing to the unique band structures and properties of graphene since it has been experimentally fabricated.[3，4]Pristine graphene is a zero-gap semiconductor and has a linear dispersion relationship near the Dirac points，[2，5]which cause electrons to behave as relativistic Dirac particles. It has also been experimentally verified that graphene has a remarkably high electron mobility at room temperature，which makes graphene an excellent semiconductor. Because of its exceptional electrical and thermal transport properties， graphene is an important two-dimensional material for exploration of physical phenomena in condensed matter，[2]and is expected to be very useful in the next-generation electronic devices.

Valley filtering effect is first reported in graphene nanoribbons，[6，7]which has been widely studied in various low-dimensional materials. Based on the semiclassical transport formulas， the valley-contrasting Berry phase effect has been taken into account in graphene nanoribbons.[8]There are also some beyond-graphene candidate materials for valleytronics applications， such as silicene，[9，10]black phosphorus，[11]and Weyl semimetals.[12，13]The interplay of spin and valley in transition-metal dichalcogenides (TMDs)can induce a valley-dependent spin-Hall effect[14]and large valley polarization.[15]

It is expected to modulate the valley-dependent transport by utilizing mechanical deformation in graphene systems.[16，17]The band structure does not change substantially for realistic strains of up to 15%.[18，19]The effect of long-range strain on electronic properties is a unique feature of graphene.[20，21]At low energies， the effects of strains can be modeled as a gauge field that acts as additional pseudomagnetic field in the momentum operators.[22]The most obvious evidence for the unusual effects of strain on the electronic states comes from scanning tunneling microscope measurements of the electronic local density of states of graphene grown on platinum.[23]An average compression of 10% creates effective fields of the same order of magnitude as the pseudo-magnetic fields observed in experiments.[24]

Although these previous works have reported many interesting results on the properties of graphene systems under strain， the effect of strain on the valley-dependent transport and separation in graphene systems has not been extensively discussed. In this study， we adopt the tight-binding modematching method and propose an efficient way to separate the Dirac fermions in different valleys by utilizing strain and the on-site energy in graphene systems. Our results show that the electrons can be dispersed by strain and the on-site energy in a valley-dependent manner. The combination of strain and onsite energy can be used to realize the effective modulation of valley-dependent transport without the need for ferromagnetic materials or magnetic fields.This phenomenon provides an alternative route to effectively modulate the valley polarizations of graphene devices.

The paper is organized as follows: In Section 2，we consider a graphene heterojunction under the influence of strain and an on-site potential applied to the central scattering region.We then calculate the strain-modulated hopping parameters based on the Slater–Koster framework. In Section 3， we analyze the dispersion relations and employ the mode-matching method to investigate the valley-dependent angular transmission. The combined effects of strain and on-site energies on the valley separation are analyzed and discussed. Finally， a summary is given in Section 4.

2. Model and analysis of strain

We consider the dynamics of electrons hopping in the honeycomb lattice governed by the nearest-neighbor tightbinding Hamiltonian[25，26]

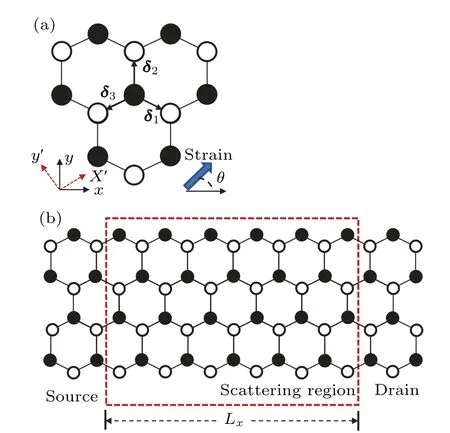
Fig. 1. (a) Honeycomb lattice geometry. The vectors δ1， δ2， δ3 connect the A sites(white)to their B-site(black)neighbors. (b)Schematic of the graphene heterojunction with an applied uniaxial strain in the central scattering region. The zigzag direction of the honeycomb lattice(x–y plane)is parallel to the x axis，and the tension is applied at an angle θ relative to the x axis.

The first term in Eq. (1) is on-site potential energy withΩbeing the magnitude of on-site energy. In practice，the onsite energy can be realized and tuned by applying top or bottom gates on the central graphene sheet. The second term is the nearest-neighbor hopping with the hopping energyt(δi j)，where the dependence oftonδi j，the vector between two sites connected byt， is explicitly stated to reflect the fact that the applied strain breaks the isotropy of the honeycomb lattice and that of the coupling strengths between a given lattice site and its three neighbors. In the central scattering region， the graphene sheet is uniformly stretched (or compressed) along the angleθrelative to thexaxis. Noticeably，we assume that there exists no strain outside the central scattering region.

When the strain is applied to the graphene system， the lattice deformation will result in changes to the vectorsδℓ(ℓ=1，2，3). The strain-dependent vectors are given byδℓ=(1+ξ)·δ0ℓ，which thus modulate the hopping terms. Accordingly，we obtain the following deformed bond lengths:

whereξκ，κ′(κ=1，2)are the matrix components of the strain tensorξin Eq.(2)，anda0=0.142 nm is the distance between nearest-neighbor lattice sites in unstrained graphene.

The change in bond lengths leads to different hopping amplitudes between each site and its three nearest neighbors. In the Slater–Koster framework，[28]the hopping terms can be obtained from the dependence of the integralVppπon the interorbital distance. A more convenient assumption is an exponential decay. Thus，we assume that，in graphene，[18]

whererℓ=|δℓ|is the bond length，and the hopping energyt0is 2.7 eV. We calculate the conductance of graphene using the Landauer formula[29]

Utilizing periodic boundary conditions along the transverse direction，an infinite graphene sheet can be modeled using a graphene nanoribbon with the zigzag chain number ofNy=2.[34]There exists an extra hopping term between the sites at the transverse boundaries， which are wrapped around and so as to overlap with each other. Thus we can introduce a Bloch phase factor ei3kya0to modify these hopping terms withkybeing the Bloch wave vector. The incident angle is defined asφ=arcsin(ky/kF)，where the Fermi wave vectorkFcan be obtained from the relationkF=2EF/(3a0t).

3. Numerical results and discussion

Fig.2. Dispersion relations plotted as a function of the wave vector kx for(a)ε=0.002 and(b)ε=0.02. The other parameters are ν=0.165，θ =45°，Ω =0 and ky=0. The red(blue)curve denotes the presence(absence)of the applied strain.

3.1. Influence of the strain on band structures

We investigate the dispersion relation of the infinite-size homogeneous graphene sheet under the influence of the strainε. The dispersion relations atky=0 are shown in Fig. 2. In the absence of strain， there is no band gap in energy bands[see blue curves] atKandK′valleys. Whenε=0.002， the energy difference between the bottom of conduction band and the top of valence band increases to about 80 meV [see red curves in Fig. 2(a)]. With the strength of strain increasing toε=0.02， the energy difference is significantly enlarged to about 308 meV.

It is natural to ask if the minima of the energy profiles for the two valleys still occur atky= 0 in the presence of strain. To clarify the effect of the strain on Dirac points， we plot equal-energy contours as a function of the wave vectorskxandkyat different strain strengths in Fig.3. We can see that whenε=0， the Dirac points ofKandK′valleys are located at(kx，ky)=(0.667，0)and(1.332，0)，respectively. When the strain increases fromε=0 to 0.005 in Fig. 3(b)， the Dirac point ofKvalley moves towards smaller value ofkxand negative value ofky，while the Dirac pointK′moves towards the opposite direction. Interestingly，in Figs.3(b)–3(d)，the Dirac points ofKandK′valleys gradually deflect from the axis ofky=0 along negative direction as the strain increases fromε=0 to 0.005， 0.015 and 0.03. It is obvious that the valley separation and transverse shifts of Dirac cones increase with the increasing strain. Because the dispersion relations in Fig.2 depict only a cut of the Dirac cone atky=0，the energy difference between the top of valence band and the bottom of conduction band does not refer to the real band gap.

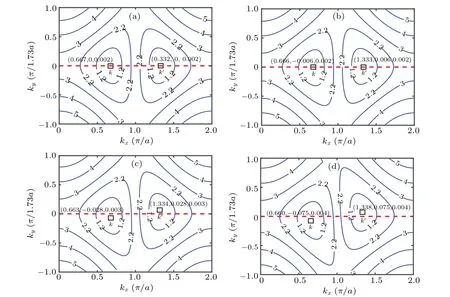
Fig.3. Contour plot of the energies as a function of the wave vectors kx and ky for different strain strengths: (a)ε=0，(b)ε=0.005，(c)ε=0.015，and(d)ε=0.03. The solid lines are equal-energy contour lines corresponding to energy values of 1.2 eV，2.2 eV，3 eV，and 4 eV. The other parameters are Ω =0，ν =0.165，and θ =45°. The black squares denote the positions of Dirac points of K and K′ valleys with the value of(kx，ky，E).

3.2. Effect of the strain on the valley-dependent transmission

Next we further study the effect of strain on the transport properties for the stretched angleθ=30°in the absence of potential energy in the central scattering section. Whenε=0，as shown in Fig.4(a)， the transmissions ofKandK′valleys are identical and equal to 1. In this case the graphene system is homogenous in the absence of any impurities and external disturbances， and the electrons are correspondingly completely transmitted without reflection. Whenεis increased to 0.003，the transmission curve ofKvalley is deflected downwards，while that ofK′valley is deflected upwards. Moreover， the maximum value of the transmission is significantly reduced to about 0.15 because of the strain. Because the graphene system is no longer a homogeneous system under the influence of the strain，which leads to the relative shift of two Dirac cones and the non-perfect transmission of electrons in two valleys.These results imply that the strain can be used to separate the Dirac fermions in theKandK′valleys，which is similar to the deflection behavior induced by magnetic fields.[35–37]

In Fig. 5， we plot the transmissions of valleysKandK′versus the incident angleφfor different stretching anglesθwhenΩ= 0. It is obvious that the transmission curves ofK(K′)valley are deflected downwards(upwards)for positive incident angles fromθ=0°to 30°，as shown in Fig.5. However，as the stretching angle increases，the value of the valleydependent transmission decreases sharply， while the incident angle associated with large values of the transmission basically keeps unchanged. When the angle is changed to negative values ofθ=0°to-30°， the transmission profiles ofKandK′valleys are pushed upwards and downwards， respectively.When the strain is applied along the zigzag (θ=0°) or armchair directionθ=90°(-90°)， the transmission profiles of two valleys are symmetrical with respective to the normal incident. The electrons inKandK′valleys therefore cannot be separated at these strain configurations. The results show that the valley-dependent transmission of electrons can be effectively tuned by changing the stretching angle in the absence of the on-site energy.

Fig.4. Valley-dependent transmission plotted as a function of the incident angle φ for(a)ε =0 and(b)ε =0.003. The other parameters are EF=15 meV，θ =30°，Ω =0 and Lx=123 nm.

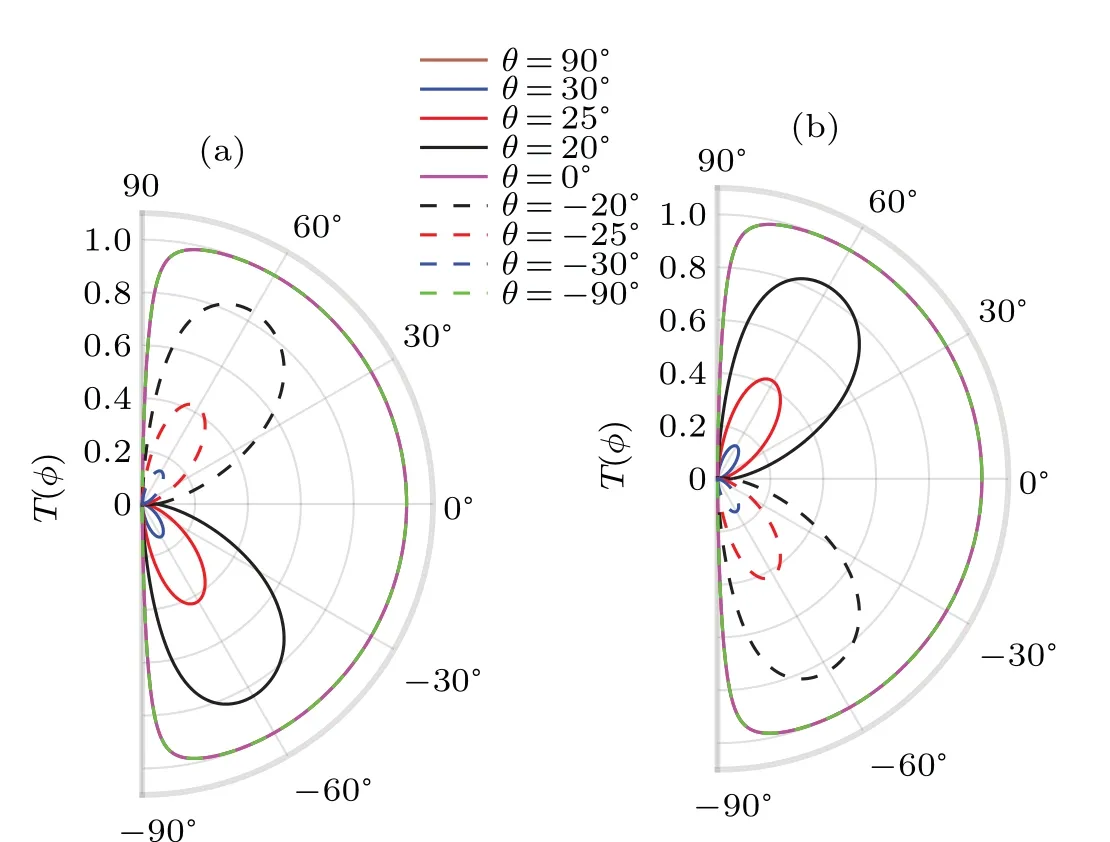
Fig.5. The transmission of(a)K and(b)K′ valleys plotted as a function of the incident angle φ for different stretching angles θ. The other parameters are EF=15 meV，ε =0.003，Ω =0 and Lx=123 nm.

Fig.6. (a)The K and(b)K′ valley dependence of the transmission versus the incident angle φ for different strengths of the strain. The other parameters are EF=15 meV，θ =30°，Ω =0，and Lx=123 nm.

To clarify the effect of the strain strength on the valleydependent transport whenΩ=0，we plot the transmission ofKandK′valleys as a function of the incident angleφfor different values of the strain strengths in Fig. 6. We find that the transmission profile ofK(K′) valley is deflected downwards(upwards)by the strain.As the strain increases fromε=0.0024 toε=0.003， the transmission magnitude of the electrons decreases gradually，but the symmetry axes of the transmission lobes are not deflected. The transmission curve ofKvalley remains within the angle interval-75°＜φ ＜-25°[see Fig.6(a)]and that of theK′valley remains within the angle interval 25° ＜φ ＜75°over the ranges of strain strengths [see Fig. 6(b)]. These results imply that when the on-site energy is zero， the transmission profile does not exhibit a deflection behavior， and the valley-dependent transmission of electrons decreases with the increasing strain strength.

Based on the above analysis， whenΩ= 0， strain can effectively cause the separation of the transmission profiles of the electrons in the two valleys， and the valley-dependent transport behavior can be effectively tuned by changing the strength of the strain. However， the symmetry axes of transmission profiles of two valleys remain unchanged when the strain angle or strength of the strain is varied.

3.3. Combined effect of the strain and on-site energy

In the above section， we can see that the strength of the strain can be used to effectively tune the valley-dependent transmission，but the change in the symmetry axis of the transmission profile is not obvious. We thus further study the combined effect of the strain and the on-site energy on the transport property. In Fig.7(a)，whenΩ=0，the transmission curve ofK(K′)valley is deflected downwards(upwards)，and the maximum value of the transmission is about 0.15. In Fig. 7(b)，when the on-site energy increases toΩ=25 meV， the transmission lobe ofKvalley is centered aroundφ=-63°，while the transmission lobe ofK′valley is centered aroundφ=63°.Moreover， the addition of the on-site energy significantly increases the maximum value of the transmission to 1. The onsite potential energy results in the formation of an n–p–n type heterojunction， which in turn leads to the recovery of perfect Klein tunneling in the considered system. These results imply that the on-site energy can result in the concentration of the electron transport inKandK′valleys in one special direction and significantly increase the transmission amplitudes，which is similar to the deflection behavior induced by electric fields in silicene systems.[10]

Fig.7. Valley-dependent transmission plotted as a function of the incident angle φ for(a)Ω =0 and(b)Ω =25 meV. The other parameters are EF=15 meV，θ =30°，ε =0.003，and Lx=123 nm.

To illustrate the effect of the on-site energy on the valleydependent transport properties，Fig.8 shows the contour plots of the transmission ofKandK′valleys as a function of the on-site energyΩand the transverse wave vectorkyfor different strain strengths. For each subgraph in Fig.8， the left and right panels are respectively associated withKandK′valleys.In this numerical calculation，θ=30°andEF=15 meV. In Fig.8(a)，whenε=0，electrons in both valleys undergo perfect transmission through the graphene heterojunction at normal incidence irrespective of the values ofΩ， which is a characteristic of Klein tunneling. It is obvious that the transmission contour plot is symmetrical aboutφ=0. Interestingly， there exists a region at 10＜Ω ＜30 meV in which the incident angle range with large transmission is contracted. As the strain increases fromε=0.001 toε=0.003，the regions with large transmission values for theKvalley gradually becomes tilted downwards，while that ofK′valley moves upwards.This tilted trend is particularly obvious in the contraction region within the interval of 10＜Ω ＜30 meV， which shows a significant effect of the strain and on-site energy.

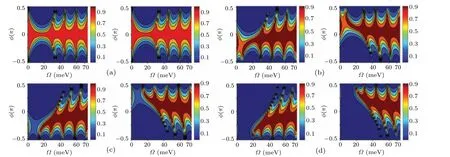
Fig.8. Contour plots of the valley-dependent transmission of the graphene heterojunction as a function of the on-site energy Ω and the incident angle φ for different strain strengths: (a)ε =0，(b)ε =0.001，(c)ε =0.002，(d)ε =0.003. The other parameters are ν =0.165，θ =30°，and Lx=123 nm. For each panel，the left and right subgraphs are associated with K and K′ valleys，respectively.

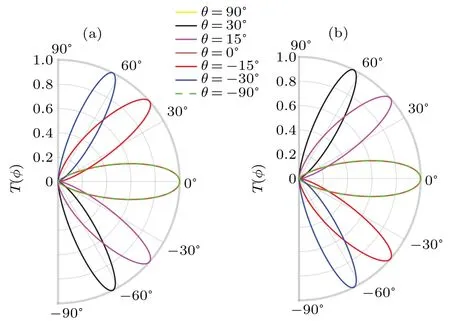
Fig.9.The transmission of(a)K and(b)K′valleys plotted as a function of the incident angle φ for different stretching angles θ. The other parameters are EF=15 meV，ε=0.003，Ω =25 meV，and Lx=123 nm.

Correspondingly， we further study the effect of the stretching angleθon the valley-dependent transport atΩ=25 meV， as shown in Fig. 9. We find that the transmission curves ofK(K′) valley are deflected downwards (upwards)fromθ=0°to 30°. However， when the stretching angle is changed to negative values， fromθ=0°to-30°， the transmission profiles ofKandK′valleys are respectively pushed upwards and downwards， respectively. When the stretching angle is increased， the transmission curves shift to larger incident angles. When the strain is applied along the zigzag or armchair direction，i.e.，atθ=0°or 90°(-90°)，the transmission profiles of two valleys are symmetrical aboutφ=0°，and there is no deflection behavior， which is a distinct anisotropy behavior for the strain modulation of the valley current. Thus，the electrons ofKandK′valleys are not separated at these strain configurations. It can be seen that the valley polarization can be effectively modulated by changing the stretching angle of the strain.

Fig. 10. The transmission of (a) K and (b) K′ valleys is plotted as a function of the incident angle φ for different strengths of the strain.The other parameters are EF =15meV， θ =30°， Ω =25 meV， and Lx=123 nm.

Similar results can be seen in Fig.10. We plot the transmission ofKandK′valleys as a function of the incident angleφfor different strengths of the strain whenΩ=25 meV. We find that the transmission profile ofKvalley is deflected downwards as the strain is increased from 0.001 to 0.003， which differs from the results in Fig.6 in which the incidence angle for the peak transmission is independent of the strain magnitude. For example， whenε=0.002， the incident angles at which electrons will be transmitted is pushed towards the angular region ofφ ＜-30°[see Fig.10(a)].This implies that theK-valley electrons will be scattered back into the left region if the incident angle is larger than a certain critical angle. The transmission profile ofK′valley is correspondingly deflected upwards under the influence of the strain. TheK′-valley electrons will be deflected back into the incident region when the incident angle is smaller than a certain angle.

Based on the above analysis， when the on-site energy is not zero， strain can be used to effectively separate electrons from different valleys， and the incident angles with high values of the transmission effectively adjusted by changing the angle and strength of the strain. This finding is of great significance for graphene-based valleytronics devices.

4. Conclusions

In summary，we have studied the effects of the strain and on-site energy on the dispersion relation and transport properties of graphene heterojunctions. It is found that the electrons can be dispersed in a valley-dependent manner by the uniaxial strain. When the on-site energy is zero and only strain acts on the graphene system，the transmission profiles are deflected to two opposite transverse directions， resulting in the separation ofKandK′valleys. When the strengths of the strain are changed，the magnitude of the transmission is significantly affected by the strain， but the transport angles associated with large values of the transmission are basically keep unchanged.When an additional on-site energy is applied to the scattering region， not only are the electrons in theKandK′valleys separated into two branches， but the transport angle of the electrons are also changed significantly as the angle and strength of the strain increases. Therefore， by combining the strain and on-site energy，an effective modulation of the valleydependent transport can be achieved by changing the strength and direction of the strain. Our results may be helpful for exploring the transport mechanism of strain-modulated graphene systems and the design of novel types of graphene-based valleytronics devices.

Acknowledgement

Project supported by National Natural Science Foundation of China(Grant No.11574067).