Manipulation of nonreciprocal unconventional photon blockade in a cavity-driven system composed of an asymmetrical cavity and two atoms with weak dipole–dipole interaction

Xinqin Zhang(张新琴)， Xiuwen Xia(夏秀文)，，†， Jingping Xu(许静平)，Haozhen Li(李浩珍)， Zeyun Fu(傅泽云)， and Yaping Yang(羊亚平)

1Institute of Atomic and Molecular Physics and Functional Materials，School of Mathematics and Physics，Jinggangshan University，Ji’an 343009，China

2MOE Key Laboratory of Advanced Micro-structure Materials，School of Physics Science and Engineering，Tongji University，Shanghai 200092，China

3College of Communication Engineering，Hangzhou Dianzi University，Hangzhou 310018，China

Keywords: unconventional photon blockade，quantum nonreciprocity，dipole–dipole interaction

1. Introduction

Photon blockade (PB)， especially one-photon blockade，provides an efficient way to produce antibunching photon source， which plays an important role in quantum metrology and quantum information technology. The first strong twomode PB has been proposed in two coupled Kerr-like nonlinear coupler， in which the quantum evolution can be closed within a finite set ofn-photon Fock states，[1]and has been observed in an optical cavity with one trapped atom.[2]Due to the potential applications in quantum communication and quantum networking，the study of PB has been paid extensive attention in various systems recently.[3–9]

Compared with the conventional photon blockade(CPB)，which is induced by anharmonicity，[10–14]quantum destruction interference induced unconventional photon blockade(UCPB) provides a strong PB effect beyond the strong coupling limitation.[15–26]Researches have shown UCPB in both cavity- and atom-driven cavity QED system recently.[27–29]However， the collective UCPB in asymmetrical cavity with and without atom-atom interaction are not revealed.

Quantum nonreciprocity in optical region is a kind of nonclassical optical nonreciprocity. The combination of PB effect and quantum nonreciprocity is prospective in achieving back-action-free quantum sensing and chiral photonic communication， which has been proposed firstly in a high-speed spinning optomechanical system，[30]and has been explored in various systems in the consequent works.[31–37]Anti-bunching or bunching photon outcomes when the incident direction is alternated. However， the vibration disturbance of mechanical rotation is always irksome and does damage to the brittle quantum procedure. As we know， Lorentz reciprocity breaking is essential to optical nonreciprocity，which is related to the collaboration of spatial symmetry breaking， time-reversal symmetry breaking and optical nonlinearity.[38–40]In this sense，the rotating ring cavity in a certain direction plays the role of breaking spacial symmetry. Producing nonreciprocal UCPB(NUCPB)without any mechanical motion，is not only beneficial to weaken the operating difficulty，but also to improve the stability of NUCPB effect.

In this work， we will introduce an all-optical NUCPB in atom–cavity QED system composed of an asymmetrical cavity and two interacting identical two-level atoms (TLAs)， where the spacial symmetry is broken naturally by asymmetrical cavity. In the atom–cavity coupling system，quantum destructive interference can lead to collective UCPB and giant NUCPB，and weak dipole–dipole interaction provides a new and feeble perturbation to quantum interference pathways.

The structure of this paper is organized as follows.In Section 2，the model of two identical atoms embedded in an asymmetrical cavity and the Hamiltonian are introduced and solved mathematically. In Section 3， two restrictions for UCPB are formulized. Controllable UCPB， as well as manipulation of normal and giant NUCPB are discussed in detail. The conclusions are given in Section 4.

2. Theoretical model

Recently， UCPB in cavity-driven QED with one or two identical TLAs in symmetrical cavity has been discussed，showing a prospective UCPB in weak coupling regimes.[28]Here，we adopt the concise model by considering two interacting TLAs with transition frequencyωaembedded in the center of a single-mode asymmetrical cavity with frequencyωc. Different with previous works，we introduce a weak dipole–dipole interactionGbetween two atoms in the asymmetrical cavity.The cavity is driven by a continuous-wave(CW)coherent field with frequencyωL， whereδa=ωa-ωL(δc=ωc-ωL) is the detuning between the atom (cavity) and input field. We respectively denotegandγas the single-atom-cavity coupling strength and atomic spontaneous decay rate，and the nonradiation dephasing effect is ignored by lettingγnon=0 in this work. The schematic diagram is shown in Fig.1(a).

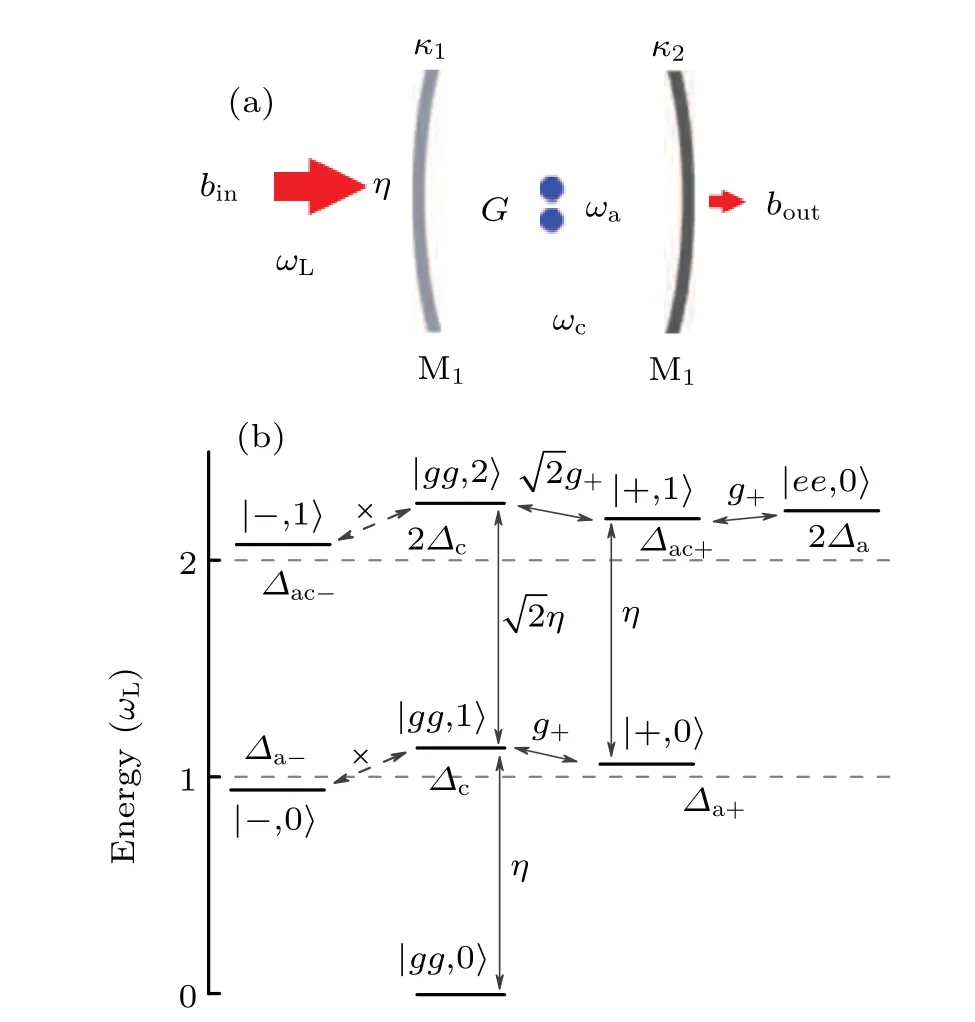
Fig.1. (a)Scheme of the asymmetrical cavity–atoms coupling system driven by CW on the left wall M1 with driving strength η. Here，cavityloss rate κ1 (κ2)represents the decay of cavity mode through M1 (M2)，ωa (ωc and ωL) the frequency of atom (cavity and light)， and G the atom-atom interacting strength.Panel(b)shows the transition pathways in the detuned cavity-driven case in weak driving limitation.

In order to break the spatial symmetry， cavity-loss ratesκ1andκ2of the cavity walls M1and M2are different from each other in general， fulfillingκi=-clnRi/2L(i=1， 2)，wherecis the velocity of light，Riis the reflectance of cavity wall Mi，andLis the effective length of the optical cavity.The cavity is symmetrical only whenκ1=κ2. We presentκave=(κ1+κ2)/2 is the average cavity-loss rate，and the total cavity-loss rate isκ=κave+κlosswhereκlossrepresents the cavity mode dissipation. We fixκloss/κ ≪1 as the highquality and low dissipation cavity is considered in this work.

In a frame rotating with the frequency of input fieldωL，the Hamiltonian of the cavity-driven system is

As mentioned in Ref. [28] and shown in Fig. 1(b)， there are three interferential pathways corresponding to the transition from|gg，1〉to|gg，2〉. One is the direct pathway of|gg，1〉 ↔|gg，2〉through pumping effect， and the other is the pathway of|gg，1〉↔|+，0〉↔|+，1〉↔|gg，2〉combined the pumping effect and atom–cavity interaction，and the third one is the pathway of|gg，1〉↔|+，0〉↔|+，1〉↔|ee，0〉↔|+，1〉↔|gg，2〉. If the three quantum channels intervene destructively and completely，the two-photon excitation will not be allowed and the probability of detecting bunching photons will be zero.

The evolution of the wave function is governed by Schr¨odinger equation. Following a much standard procedure which has been applied widely in previous works，the equation can be solved analytically and be simulated numerically. By setting column vectors asC=（cgg，1c+，0cgg，2c+，1cee，0

）T andA=（-ηcgg，00 0 0 0）T， we can get the dynamical equations for the amplitudes of each state reading

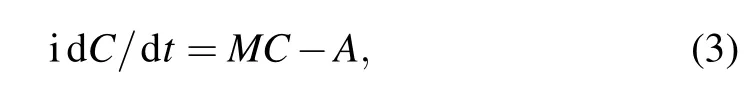
where the 5×5 matrixMis the truncated Hamiltonian in the two-exciton framework reading

whereCiis thei-th component of vectorC，D=det(M) andDi=det(Mi)are the determinants ofMandMi，whereMiis the transformation of matrixMby replacing thei-th column with column vectorA. Then， one can get the intensity of the cavity fieldnc=〈a†a〉as

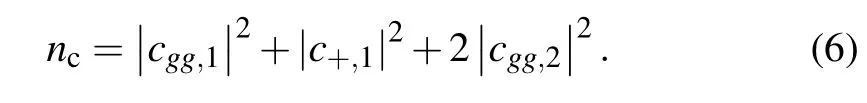
It indicates that the cavity filed is composed of both bunching and anti-bunching components in general. By introducing the output filed operatorboutand applying the quantum input–output theory，[41]we can get

The antibunching light without any bunching photon can be obtained by solving eitherg(2)(0)=0 orD3=0. Restrictions for fully antibunching output can be obtained which is to be discussed in the following section.

For simplicity and without loss of generality， we focus on the asymmetrical cavity withκ1＜κ2to discuss the phenomenon of NUCPB.In this case，UCPB in asymmetrical cavity for the backward case can be easily obtained by alternatingκ1withκ2.We will in detail show the manipulation of controllable collective UCPB and NUCPB in the following section by taking or not taking the atom–atom interaction into account.

3. Manipulation of UCPB and NUCPB

3.1. Without atom–atom interaction

The atom–atom interaction makes atoms to excite each other by dipole–dipole coupling. From the energy level diagram in the collective picture， atom–atom interaction pushes down the state|-，n〉while pulls up|+，n〉a shift ofG. Such push-and-pull effect of energy level can be used to manipulate UCPB. However， dipole–dipole coupling only occurs when two atoms are cold and close enough， and can be ignored in most common cases. Therefore，we first discuss the phenomena of UCPB and NUCPB in the absence of atom–atom interaction by settingG=0.

After solvingD3=0， we can getη2-g2-ΔaΔac=0.Letting the real and imaginary parts equal to zeros，two restrictions for producing of UCPB can be obtained mathematically，which is exactly the same to those in single-atom case.[42]The first restriction is the frequency condition

Here， we rewriteδac=δa+δc. It shows that the detunings(δa，δc)and decay rates(γ，κ)are combined together to match the restriction in cavity-driven case， which is different to that in atoms-driven case.[28]However， in the resonant case withδa=δc=0，the frequency restriction is always matched naturally.

The second one is the intensity restriction，

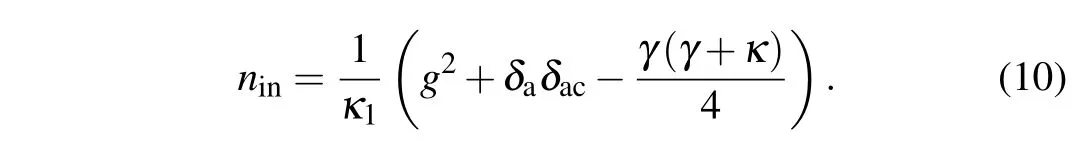
It indicates that the optimal atom–cavity coupling strength to get the fully antibunching output light relies on the incident direction，

In the asymmetrical cavity，the optimal atom–cavity coupling strength shall be split into two values according to incident direction， i.e.，gopt-1for the forward case andgopt-2for the backward case，fulfillinggopt-1＜gopt-2as we setκ1＜κ2.

From now on，we normalize all the parameters by settingκ ≡1 andκloss=0.02 for simplicity and set the asymmetrical cavity withκ1=0.36 andκ2=1.60. In order to show UCPB in asymmetrical cavity intuitively， we plot the functions ofg(2)(0)as a function of atom–cavity coupling strengthgwith respect to one-atom and two-atom cases in both forward and backward directions， as shown in Fig.2(a). We focus on the resonant case withδa=δc= 0 to match the frequency restriction naturally，γ=0.1 as well asnin=0.04 in present numerical simulation.

As expected， optical atom–cavity coupling strengthsgopt-1≈0.2047 andgopt-2≈0.3025 separate from each other when light incidents on different walls in both one-atom and two-atom cases.In the asymmetrical cavity，spatial asymmetry breaking opens a new access to control UCPB by asymmetric cavity-loss rates.

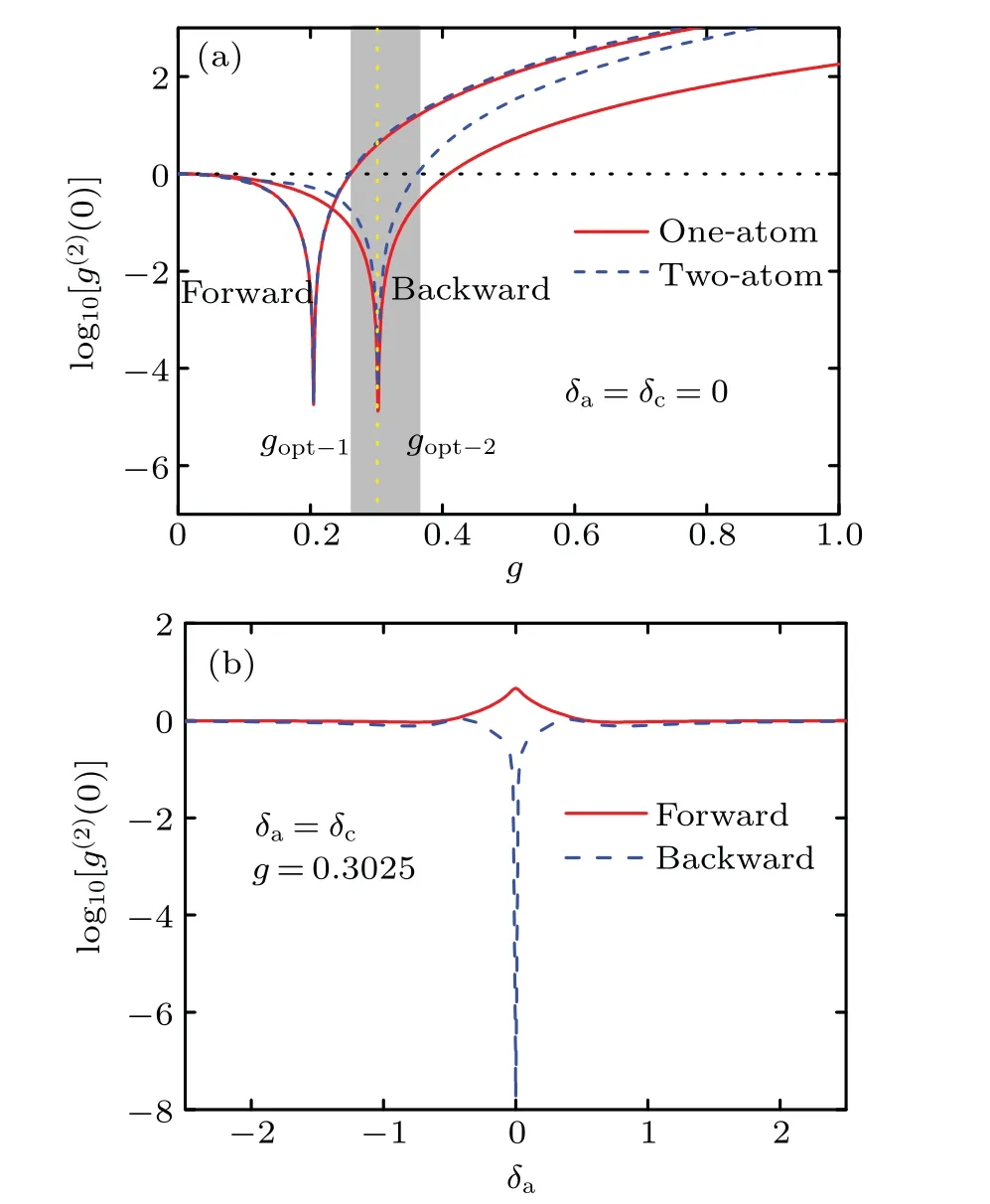
Fig.2. UCPB and NUCPB in asymmetrical cavity without atom–atom interaction. In panel (a)， the red solid curves are g(2)(0) for one-atom case while the blue dashed ones are for two-atom case with δa =δc =0. Operating regime for normal NUCPB is covered by the gray rectangle while the yellow dotted line presents a giant NUCPB. Panel (b)shows g(2)(0)for both forward and backward incident directions in twoatom case by fixed δa =δc and g=0.3025. In both panels， the total cavity-loss rate is fixed and normalized as unit，the asymmetrical cavity is κ1 =0.36 and κ2 =1.60， and the other parameters are κloss =0.02，γ =0.1 and nin=0.04.

Compared the results in both two-atom and one-atom cases， two trapped non-interaction atoms do not harm or improve noteworthily the effects of UCPB and NUCPB as the restrictions for UCPB in both cases change nothing. It indicates that one can using two non-interaction atoms to replace a single atom in generating controllable UCPB and NUCPB.

3.2. With dipole–dipole interaction

Compared the UCPB restrictions with and without dipole–dipole interaction，the later ones are much complex and rigorous to match simultaneously since dipole–dipole interaction disturbs the quantum interfering pathways by the pushand-pull effect.

In order to show the influence of atom–atom interaction on UCPB clearly，we plotg(2)(0)against detuningsδaandδcin Figs.3(a)and 3(b). As a smallerγis beneficial to produce UCPB in weak coupling regime，we setγ=0.1，g=0.25 andη=0.1980 in the following numerical simulations， and setG=0 in Fig. 3(a) whileG=0.01 in Fig. 3(b). Due to the push-and-pull effect induced by weak dipole–dipole interaction，UCPB regime is compressed more or less whenG=0.01，and the minimum ofg(2)(0)is pull down a lot which indicates an improving NUCPB on some special points. NUCPB is promoted when the two complex UCPB restrictions are matched，while it may be suppressed when restrictions are mismatched.In general， a suppressed or promoted UCPB is depending on the working parameters.

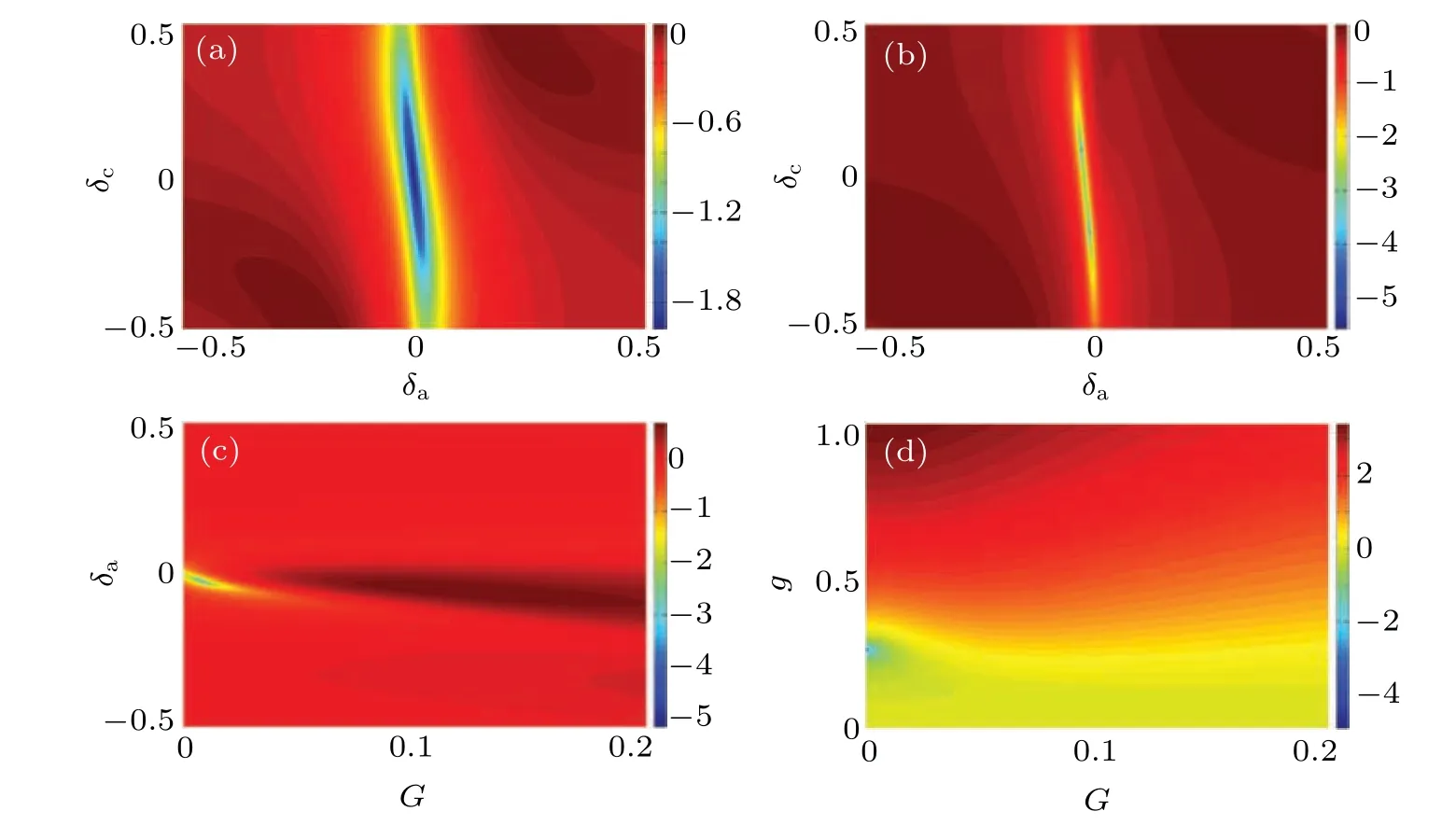
Fig.3.Controllable UCPB with atom–atom interaction.Panels(a)and(b)are g(2)(0)against atom and cavity detunings for G=0 and G=0.01.Panel(c)is g(2)(0)against G and δa. Panel(d)is g(2)(0)against G and g. We set g=0.25 in panels(a)–(c)，δc=δa in panels(c)and(d). In all panels，we fix κ =1，κloss=0.02，γ =0.1 and η =0.1980.

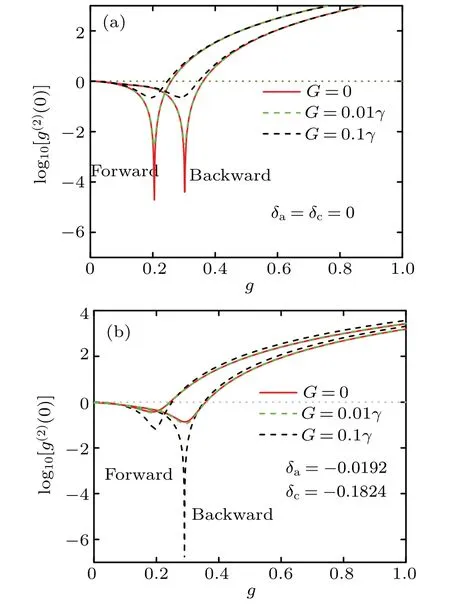
Fig. 4. Manipulation of NUCPB in asymmetrical cavity with atom–atom interaction. The red solid curves are g(2)(0) for G=0 while the green and black dashed ones are for G=0.01γ and 0.1γ. Panel(a)is a suppressed NUCPB for δa=δc=0 and nin=0.04 while panel(b)is a promoted NUCPB for δa=-0.0192 and δc=-0.1824 and nin=0.04.The other parameters are same as those used in Fig.2(a).

Compared with previous works of the NUCPB within the rotating optomechanical systems，[31–33]our model is alloptical without any mechanical rotation， and provides a method to manipulate UCPB by controlling atom–atom interaction. Using the existing magneto-optical trapping technology， cold atoms can be captured and moved into the optical microcavity. Therefore， it is feasible to carry out our prediction under careful designing.To our surprise，the experimental demonstration of NUCPB may has been carried out partially in atoms–cavity coupling system while the parameters are imperfect to produce giant quantum nonreciprocity.[43]

4. Conclusion

In conclusion， we have proposed a cavity-driven QED model combined an asymmetrical Fabry–Perot cavity and two identical TLAs to generate controllable UCPB and NUCPB.In the case of atom–atom direct interaction absence， the frequency and intensity restrictions of UCPB can be specified，which are identical to the restrictions of UCPB when single atom embedded. Giant NUCPB exists due to the splitting of optimal atom–cavity coupling strength in proper parameters regime. However， when a weak atom–atom interaction disturbing the quantum interference pathways is taken into account， two restrictions of UCPB are modified complexly，which are rigorous to be matched simultaneously. It makes the region of UCPB to be compressed more or less while the effect of UCPB can be improved as a smaller minimum ofg(2)(0) may be presented. We also examine the influence of NUCPB by weak atom–atom interaction and giant NUCPB occurs when atom–atom interaction is weak enough. In general，whether the giant NUCPB is suppressed or promoted depends on the working parameters.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grants Nos. 12164022， 11864018， and 12174288) and the Fundamental Research Funds for the Provincial Universities of Zhejiang Province， China (Grant No.GK199900299012-015).