Goos–H¨anchen and Imbert–Fedorov shifts in tilted Weyl semimetals

Shuo-Qing Liu(刘硕卿)， Yi-Fei Song(宋益飞)， Ting Wan(万婷)，You-Gang Ke(柯友刚)， and Zhao-Ming Luo(罗朝明)，2，‡

1Key Laboratory of Hunan Province on Information Photonics and Freespace Optical Communications，School of Information Science and Engineering，Hunan Institute of Science and Technology，Yueyang 414006，China

2School of Physics and Chemistry，Hunan First Normal University，Changsha 410205，China

Keywords: Goos–H¨anchen shift，Imbert–Fedorov shift，Weyl cone tilting，chemical potential

1. Introduction

Reflection of plane waves can be simply described by geometric optics. However， for laboratory reflected beams with a finite width，it does not obey Snell’s law and exhibits peculiar physical effects. Goos–H¨anchen(GH)shift is considered as one of the representative physical phenomena due to angular spectrum diffraction，which refers to the longitudinal shift of the beam transmission path parallel to the geometric optical path for total or partial reflection.[1，2]It was first found experimentally by Goos and H¨anchen in 1947，and theoretically demonstrated by Artmann in 1948.[3]Soon after， it was observed that there was also a transverse shift in the direction perpendicular to the geometric optical path，which was predicted by Fedorov in 1955 and experimentally demonstrated by Imbert in 1972，called the Imbert–Fedorov(IF)shift.[4–6]The GH and IF effects have attracted wide attention in physics and have been studied at different interfaces in recent decades， such as hybridized topological insulator，[7]metasurface，[8，9]photonic crystal，[10，11]temporally dispersion attenuation material，[12]graphene.[13–19]Specifically in these studies，GH and IF shifts were tuned by magnetic field and chemical potential，[7，17–19]and often used as effective probes in precision metrology of material structural parameters since they were sensitive to material properties.[15，16]

Weyl semimetal (WSM)， an emerging topological material who takes non-mass Weyl fermions as quasi-particles， is also known as “three-dimensional graphene”. The Hamiltonian of WSM extends to three-dimensions leading to extraordinary physical properties different from two-dimensional materials，such as anomalous Hall effect，[20]peculiar electromagnetic response，[21]and negative magneto-resistivity.[22]Recently， researchers have demonstrated that there also exist beam shifts relative to the geometric path after reflecting on the WSMs interface.[23–26]Jianget al.theoretically predicted the existence of GH and IF shifts in WSMs.[23]Yeet al.studied the GH and IF shifts in WSMs，and revealed the role of the separation of the two Weyl points in the beam shifts.[24]Note that these studies mainly focus on the ideal type-I WSMs， where the dispersion of the corresponding Weyl fermions satisfies the Lorentz symmetry and has no tilting and doping. Nonetheless，the dispersion of Weyl fermions is generally tilted with broken Lorentz symmetry. Eventually， when the tilting is strong enough， the Weyl cones will turn over and cause the WSM from type I to type II，[27，28]thus leading to some new physical phenomena such as Klein tunneling，[29]epsilon-near zero response.[30]Researchers have studied novel photoelectric effects in tilted WSMs in succession.[31–33]Sonowalet al.studied the optical activity of tilted WSMs， and demonstrated the presence of a giant Kerr effect in this material.[31]Xinget al.found that the type-II WSM TalrTe4has superconducting properties.[33]We discussed the role of Weyl cone tilting in photonic spin Hall effect in tilted WSMs，and proposed a new method for determining the type of WSMs and sensing the tilt degree of Weyl cone precisely.[34]In spite of this， the beam shifts are rarely discussed in the case of tilted Weyl nodes，while the study plays an important role for the more comprehensive grasp of the light-WSMs interaction and the related application.

In this paper，we extend the beam shift models from ideal type-I WSMs to tilted type-I and type-II WSMs， and systematically investigate the roles of Weyl cone tilting and chemical potential in the GH and IF shifts. Based on the models with fixed incident photon frequency， we achieve the relation between Weyl cone tilting and conductivities of WSMs， and further obtain the relationship between the Weyl cone tilting and the reflection coefficients. Subsequently， the influences of Weyl cone tilting and chemical potential of WSMs on the GH and IF shifts are discussed and summarized. The results show that GH and IF shifts almost present symmetry distribution relative to Weyl cone tilting， and chemical potential can adjust the distribution. In addition，we extend the discussions to the influences of frequency on the GH and IF shifts.

2. Theoretical analysis

Figure 1(a) shows schematic of the light reflected in a WSM-substrate structure. The GH and IF effects generate when a Gaussian beam reflects on the WSM-substrate structure. Here，ΔGHandΔIFrepresent the spatial shift of the GH and IF effects，respectively;ΘGHandΘIFrepresent the angular shifts of the GH and IF shifts;the coordinate frames(xi，yi，zi)and(xr，yr，zr)are central wave vectors of the incident and reflected wavepacket; andθiis the incident angle. Here， we consider Weyl points existing in pairs with opposite chiralityξ=±1，positioned at(0，0，∓b)in bulk Brillouin zone，andbindicates the Weyl points separation. The low-energy Hamiltonian of the Weyl points with chiralityξcan be written as

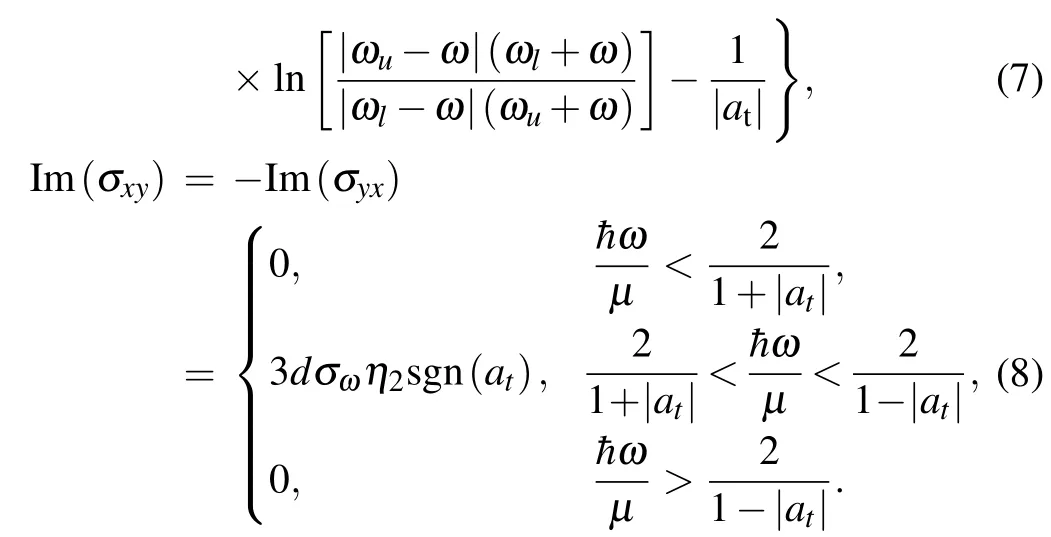
For type-II WSM with|at|＞1，the longitudinal and Hall conductivities are given by[31]

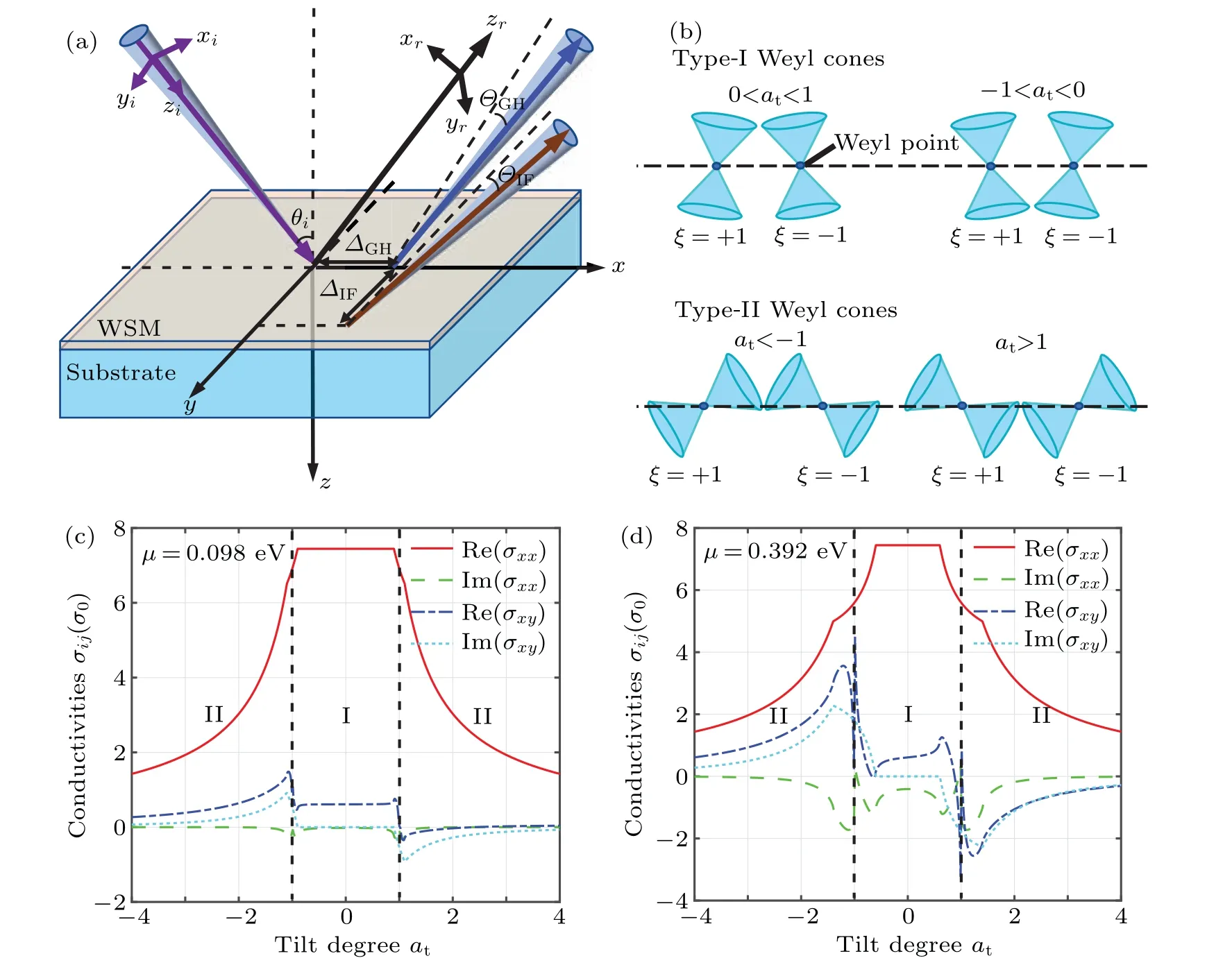
Fig. 1. (a) Schematic of the light reflected in a WSM-substrate structure. After the Gaussian beam reflects on the structure， GH and IF effects generate and induce the spatial beam shifts ΔGH，ΔIF and angular shifts ΘGH，ΘIF;θi is the incident angle. (b)Schematic of a pair of Weyl points with opposite chirality ξ =±1 and titled Weyl cones. The tilt degrees of type-I and type-II Weyl cones are|at|＜1 and|at|＞1，respectively. (c)and(d)Dependences of WSMs conductivities on tilt degrees at at chemical potentials μ=0.098 eV and μ=0.392 eV，respectively. Red lines and green lines describe the real and imaginary parts of longitudinal conductivity(i.e.， Re(σxx)and Im(σxx))， respectively. Blue lines and cyan lines represent the real and imaginary parts of Hall conductivity(i.e.，Re(σxy)and Im(σxy)). These conductivities are in units of σ0.

Previous studies have shown that the optical conductivities play an important role in influencing the reflection coefficients， and may then affect the optical effects at the material surface.[31–34]For the purpose of establishing the models of GH and IF shifts in tilted WSMs more comprehensively，it is necessary to solve the reflection coefficients of WSMs and investigate the relationship between these coefficients and WSMs conductivities.

Solving the boundary condition expressions by considering the electromagnetic field and Ohm’s law，[39]the Fresnel reflection coefficients of WSM-substrate can be expressed as[31]

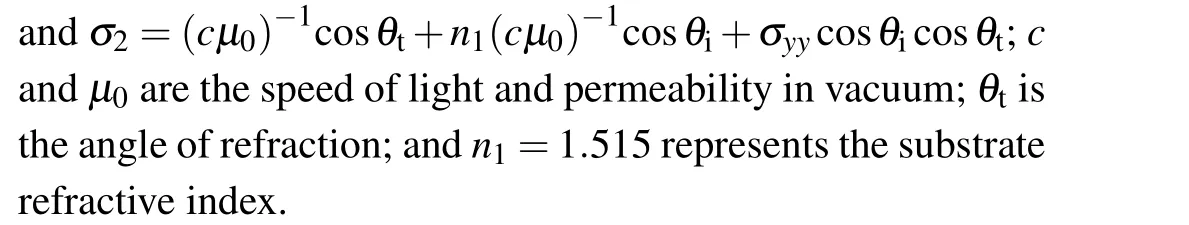
Figure 2 shows the variation of the corresponding reflection coefficients modulus as functions ofatat different chemical potentials ofμ= 0.098 eV andμ= 0.392 eV. Here，Figs. 2(a)–2(c) are reflection coefficients in the case ofμ=0.098 eV，while Figs.2(d)and 2(f)are those ofμ=0.392 eV.It is worth noting that the reflection coefficientsrps=-rspaccording to Eqs.(17)and(18)，so that we only plot the reflection coefficientsrpp，rsp，rss. From Fig. 2， all reflection coefficients almost present symmetry distribution with the change ofat，which are almost invariant in type-I WSMs and decrease symmetrically in type-II WSMs. These phenomena are largely owing to the different dependence properties of conductivities onatin type-I and type-II WSMs.Meanwhile，there is an obvious boundary between the reflection coefficients of type-I and type-II WSMs， especially the drastic change of the modulusRpsyielded here. These trends are very similar to the boundary behavior of the Hall conductivity in Fig. 1， so it can be speculated that the cross reflection coefficient is mainly correlated with the Hall conductivity.

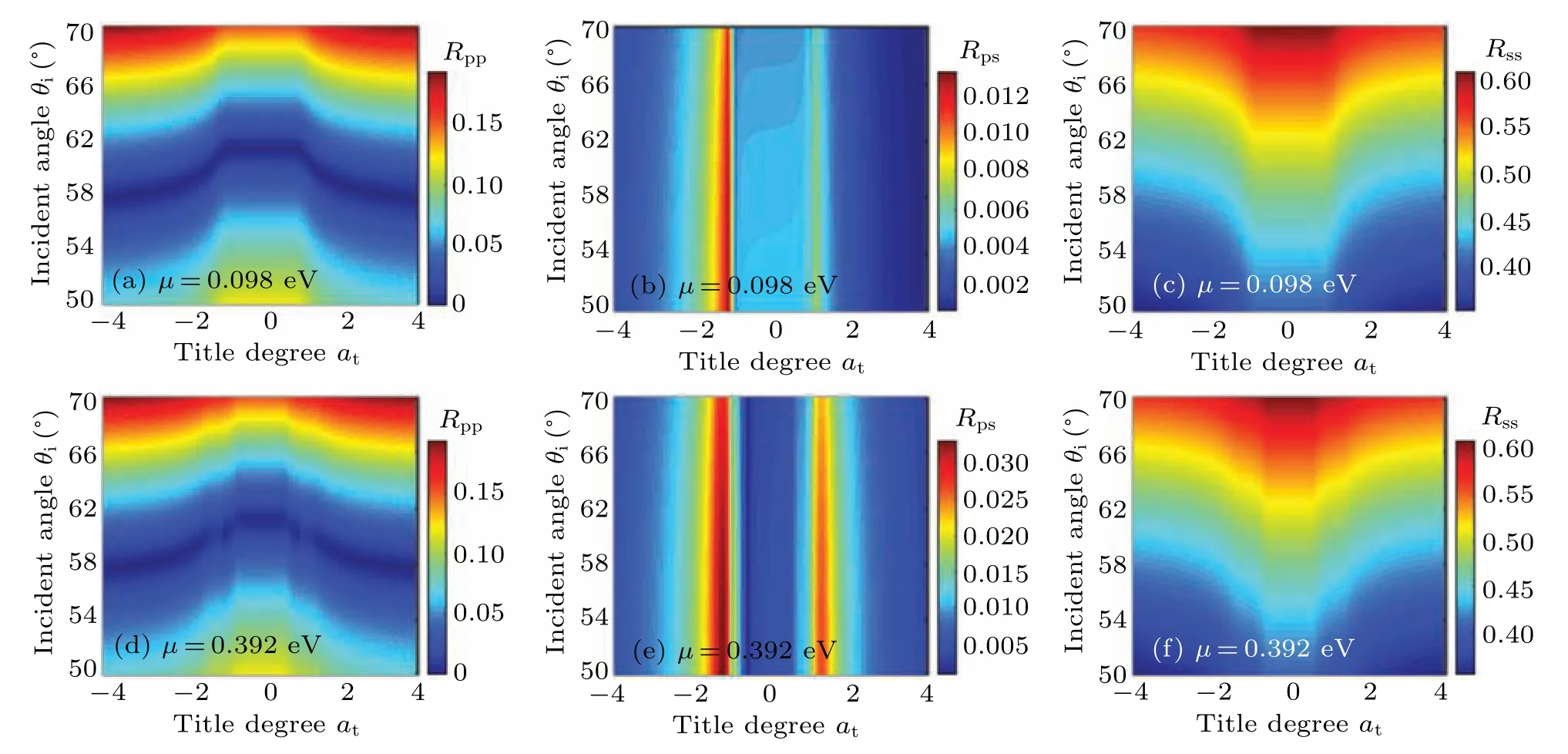
Fig.2. Pseudo-color images of modulus value of reflection coefficients Rpp，Rps，Rss as functions of the tilt degrees at and the incident angles θi at different chemical potentials: (a)–(c)μ =0.098 eV，(d)–(f)μ =0.392 eV.

Note that the incident angle corresponding to theRpp=0 is usually called the Brewster angle.[25]Here， the Brewster angle increases from 58°to 61.3°and then decreases to 58°，which also presents symmetric distribution with the variation ofat， approximating to the variation of Re(σxx)， so that the Brewster angle is closely related to Re(σxx). In comparison of the reflection coefficients atμ=0.098 eV in Figs. 2(a)–2(c)withμ=0.392 eV in Figs.2(d)–2(f)，the boundary of reflection coefficients in type-I and type-II WSMs expand with the increase ofμ， and the peak value ofRpsin the boundary increases correspondingly. It is consistent with the trend of Hall conductivity withμin Figs. 1(c) and 1(d)， and demonstrates again that Hall conductivity plays a major role in affecting cross reflection coefficients.

So far，we have established the reflection models in tilted and doped WSMs，and discovered the relationship between the conductivities and the reflection coefficients. In the following statement， we will further explore the influences of the Weyl cone tilting and chemical potential on the GH and IF shifts based on these models， and discuss the role of the frequency in the beam shifts of tilted WSMs， and regularize the results systematically.

3. Results and discussion

In this section，we establish the beam models of GH and IF effects in tilted and doped WSMs. Considering the Gaussian beam incidence，the angular spectrum expression is

Here，kix=k0cosθiandkiy=k0sinθiare the components of the incident beam vector in thexrandyrdirections， respectively;k0=2π/λdenotes the wave vector of vacuum; andw0=18 μm is the beam waist. Subsequently， we calculate the GH and IF shifts according to the beam angular spectrum and discuss the role of Weyl tiltingatand chemical potentialμin the GH and IF shifts at a fixed frequency ¯hω=1.96 eV withλ=632.8 nm， and extend to discuss the influences of frequency on the beam shifts.

3.1. Influences of Weyl cone tilting and chemical potential on the GH shifts in tilted WSMs

The GH effect appears when the beam is reflected on the tilted WSMs， and the expression for the relation between the reflected angular spectrum and the incident angular spectrum can be obtained as follows:[21]

To simplify the calculation， we consider the incident beam with horizontal linear polarization，i.e.，α=1，β=0. According to the boundary conditionskrx=-kixandkry=-kiy，and substituting Eqs.(19)and(21)into Eq.(20)，the angular spectrum of the reflected beam can be further expressed as

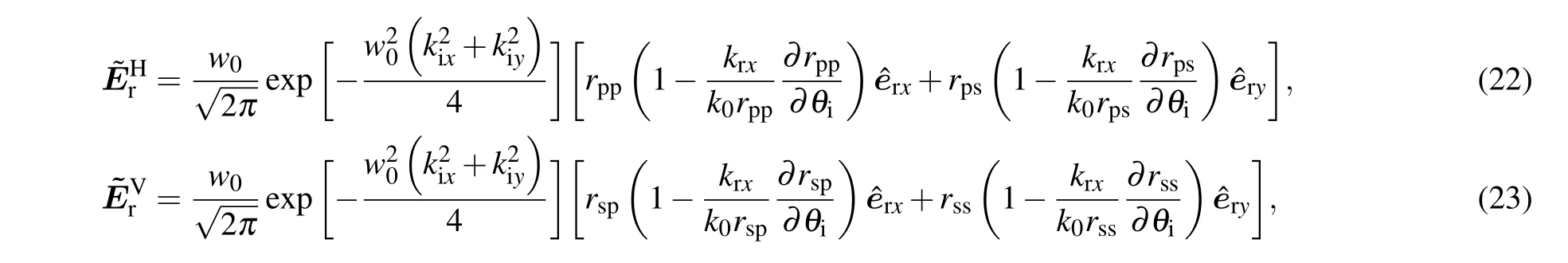
wherekrxandkryare the reflected wave vector inxrandyrdirections. Taking the paraxial approximation into account， the complex amplitude of the reflected beam is given by

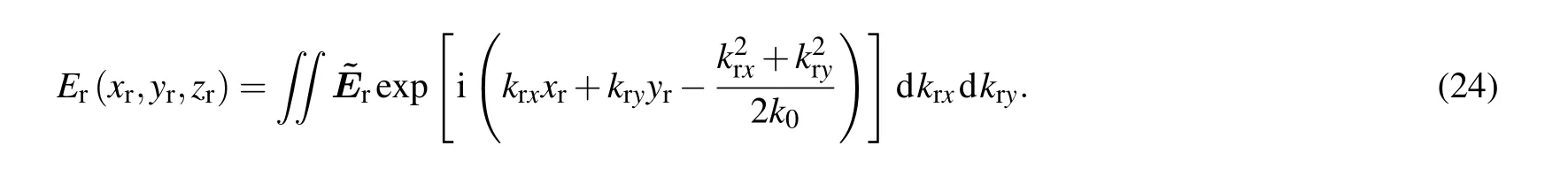
Substituting Eqs.(22)and(23)into Eq.(24)，the intensity distribution of beamI(xr，yr，zr)can be obtained. At any given planezr=const，the GH shift of field centroid can be defined as

From Eq.(25)，the GH spatial and angular shifts can be finally given by

Here，zR=k0w20/2 is the Rayleigh length，ψA=Im(1/rA×∂rA/∂θi)andρA=Re(1/rA×∂rA/∂θi).

We further study the influences of Weyl cone tiltingatand chemical potentialμon the GH shifts. Figure 3 shows the GH shifts as functions ofatandθiin different chemical potentials. Here，Figs.3(a)and 3(b)are GH spatial and angular shifts in the case ofμ=0.098 eV， respectively. Figures 3(c)and 3(d)are those ofμ=0.392eV. From Figs.3(a)and 3(b)，it is found that the GH spatial shifts are mainly concentrated in type-I WSM，while the angular shifts are significant in WSMs of both types I and II.These shifts almost show symmetry distribution respect toat=0. At a fixed angle of incidence near the Brewster angle，as|at|increases，the spatial shifts first remain unchanged in the type-I WSMs，then increase to the peak near the boundary of type-I and type-II WSMs due to the drastic change of cross reflection coefficient，and finally reduce in type-II WSMs. Here， the peak of the spatial shifts is about-4100 nm atat=-0.91. Angular shifts barely change withatin type-I WSMs but are sensitive toatin type-II WSMs.These trends arise because the conductivities keep stable in type-I WSMs and gradually decrease with tilt degree in type-II WSMs in Figs.1(c)and 1(d).Specifically，in the case ofθiless than or near the Brewster angle of type-I WSM(θi=61.3°)，as|at|increases，the angular shifts increase first to the peak，then quickly switch to the reverse direction peak and gradually decrease. The angular shifts yield by up to 5600 μrad during these processes. It is noteworthy that there are small differences in GH shifts foratwith the same size and the opposite sign.Comparing the cases ofμ=0.098 eV withμ=0.392 eV[see Figs.3(c)and 3(d)]，we conclude that as chemical potential increases， the spatial shifts increase significantly and can reach up to-7589.66 nm atat=-0.61， while the angular shifts reduce continuously. Simultaneously，the boundary between type-I and type-II WSMs extends，because the boundary ofrpswidens withμ.

From the above analysis， we can find that the GH shifts almost present symmetric distribution relative to Weyl cone tilting. The GH shifts in type-I WSMs almost show no dependence on Weyl cone tilting，whereas the shifts in type-II WSMs change significantly with Weyl cone tilting. Meanwhile，there exists drastic change of GH shifts in the boundary between the two types of WSMs， and the peak value of mutations can be manipulated significantly by adjusting chemical potential.These phenomena are mainly related to dramatic variations of conductivities induced by Weyl cone tilting and chemical potential. Furthermore， it can be provided as a reference to the determination of WSMs’ type due to the distinct difference in the tilt-dependent GH shifts in type-I and type-II WSMs，which has important implications for the study of WSMs and the application of related optoelectronic devices.

Fig.3. Pseudo-color images of GH shifts as functions of the tilt degrees at and the incident angles θi at different chemical potentials μ. (a)and(b)The spatial shift ΔGH and angular shift ΘGH in the case of μ =0.098 eV. (c)and(d)The GH shifts in the case of μ =0.392 eV.

3.2. Influences of Weyl cone tilting and chemical potential on the IF shifts in tilted WSMs

When the light reflects in tilted WSMs， the IF effect generates with an extra more transverse part perpendicular to the geometric path compared with the GH effect， thus the relation between reflected angular spectrum and the incident angular spectrum can be expressed as[34]

Here，the reflection coefficientrps=-rsp. After substituting Eqs.(19)and(21)into Eq.(28)，the angular spectrum expression of the reflected beam can be further expanded to

After substituting Eqs.(29)and(30)into Eq.(24)，the reflected field expression for the light in position space can be written as

At any given planezr=const，the transverse shift of f ield centroid can be def ined as

Combined w ith Eqs.(33)–(36)，it can be noted that the IF spatial shifts exist obviously while the angular shifts are null. So far，we have established the calculation model of IF shifts in tilted WSMs.

Fig.4. Pseudo-color images of IF shiftsas functions of the tilt degrees a t and the incident anglesθi atdifferentchem ical potentialsμ.(a)and(b)The spatialshifts of the incident beams w ith left-handed circular polarization Δand right-handed circular polarization Δ in the case of μ =0.098 eV.(c)and(d)The IFshifts in the case of μ =0.392 eV.

We now focus on discussing the influence of Weyl cone tiltingaton the IF spatial shifts. Figures 4(a) and 4(b) describe the IF shifts as functions ofatandθifor left-handed and right-handed circular polarization incidences by fixingμ=0.098 eV. It is shown that the IF shifts are almost invariant in type-I WSMs while change dramatically in type-II WSMs， and almost exhibit obvious symmetry relative to theat=0. These trends are mainly attributed to the nearly symmetric distribution of WSMs conductivities in Figs. 1(c) and 1(d). To study the influence ofμon IF shifts， we also plot the IF shifts atμ=0.392 eV，as shown in Figs.4(c)and 4(d).The results reveal that the peak of the IF shifts is almost not dependent onμand the shifts still show symmetry distribution relative toat， but the symmetry axis produces a slight shift from the previousat=0. Note that in our case， strange IF shifts near Brewster angle almost do not exist for circular polarization incidences. For linear polarization incidence， a phenomenon similar to the IF effect， called the photonic spin Hall effect， may be produced in tilted WSMs because of the spin-orbit coupling. Meanwhile the Brewster angle will affect the spin-orbit coupling and lead to a peculiar spin-dependent splitting.[40，41]

It is worth mentioning that the IF shift is weak. To describe influences of Weyl cone tiltingatand chemical potentialμon IF shifts more clearly， we further plot the IF shifts (both left- and right-handed circular polarization incidences) as functions ofatin the cases ofμ=0.098 eV andμ=0.392 eV，as shown in Figs.5(a)and 5(b).

Referring to the special angle ofθi=61.3°in Fig.3，the incident angles here are fixed as 58°(less than 61.3°)， 61°(near 61.3°)， and 64°(larger than 61.3°). From Fig. 5(a)， IF shifts all keep stable in type-I WSMs first for arbitrary circular polarization incidences， and then decrease with the increase ofatin type-II WSMs. These shifts almost show symmetry distribution relative toat=0. It is worth noting that the IF shifts exist small differences in IF shifts foratwith the same size but opposite symbols (the same|at|). Furthermore，the IF shifts gradually decrease with the increases ofθidue to inversely proportional relations betweenθiand cotθiin Eqs.(33)and(35). Compared the IF shifts of the left-handed and right-handed circular polarization incidences，the IF shifts are symmetric relative to the coordinate origin at any fixed incident angle. Then， we further discuss the influence ofμon IF shifts by comparing Fig.5(a)with Fig.5(b). It is found that with the increase ofμ， the symmetric distribution of the IF shifts still remains，but the symmetry axis of IF shifts products a slight movement relative toat=0. Specifically， the symmetry axis moves to the left or the right relative toat=0 in the cases of the left-or right-handed circular polarization incidences. The above analyses provide a new reference to revisit the IF shift in WSMs. Since the IF shift is too weak to be observed， effective experimental detection can be performed by using a weak signal amplification technique called quantum weak measurement.[39]The application of this technique can also be extended to optical effects observations in other approximate topological materials of WSMs.

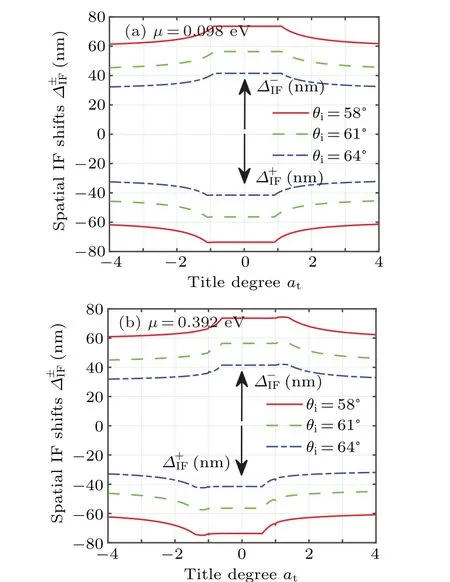
Fig. 5. Dependences of IF shifts on the tilt degrees at and the incident angles θi at different chemical potentials μ. (a)and(b)The spatial shifts of the incident beams with left-handed circular polarization Δ+IF and right-handed circular polarization Δ-IF in the case of μ =0.098 eV.(c)and(d)The IF shifts in the case of μ =0.392 eV.

3.3. Influences of frequency on the GH and IF shifts in tilted WSMs

The influences of Weyl cone tilting on beam shifts in both doped type-I and type-II WSMs，have been discussed systematically，in the case of He–Ne laser incident with beam intensity¯hω=1.96 eV and frequencyω=2.98×1015Hz.It is also worth noting that the photon frequency， as an indispensable parameter of beam intensity， may change the physical properties of the optical material and exert an influence on lightmatter interaction. Consequently， we additionally expand the frequency range and discuss the role of the frequency on the reflection coefficients and beam shifts in tilted WSMs.

By fixing the chemical potential asμ=0.098 eV，we discuss the variation of the reflection coefficients modulusRpp，Rps，Rssas functions of frequency in type-I and type-II WSMs as shown in Fig. 6. Here Figs. 6(a)–6(c) show reflection coefficients in the case ofat= 0.5 (type-I WSMs)， whereas Figs. 6(d)–6(f) show those ofat=2.0 (type-II WSMs). The Brewster angle (Rpp= 0) in both type-I and type-II WSMs becomes larger with the increase of photon energy， and the larger trend in type-I WSMs is more obvious than that in type-II WSMs [Figs. 6(a) and 6(d)]. Meanwhile， as the frequency increases at any certain incident angle，Rpsdecreases gradually[Figs.6(b)and 6(e)]，andRssshow a weak increase[Figs.6(c)and 6(f)]. Overall， combining with the previous study， it can be speculated that the photon frequency may also play its interesting function in influencing the beam shifts，especially near the Brewster angle. Subsequently， we discuss the influences of the frequency on the GH and IF shifts in tilted WSMs near the Brewster angle.

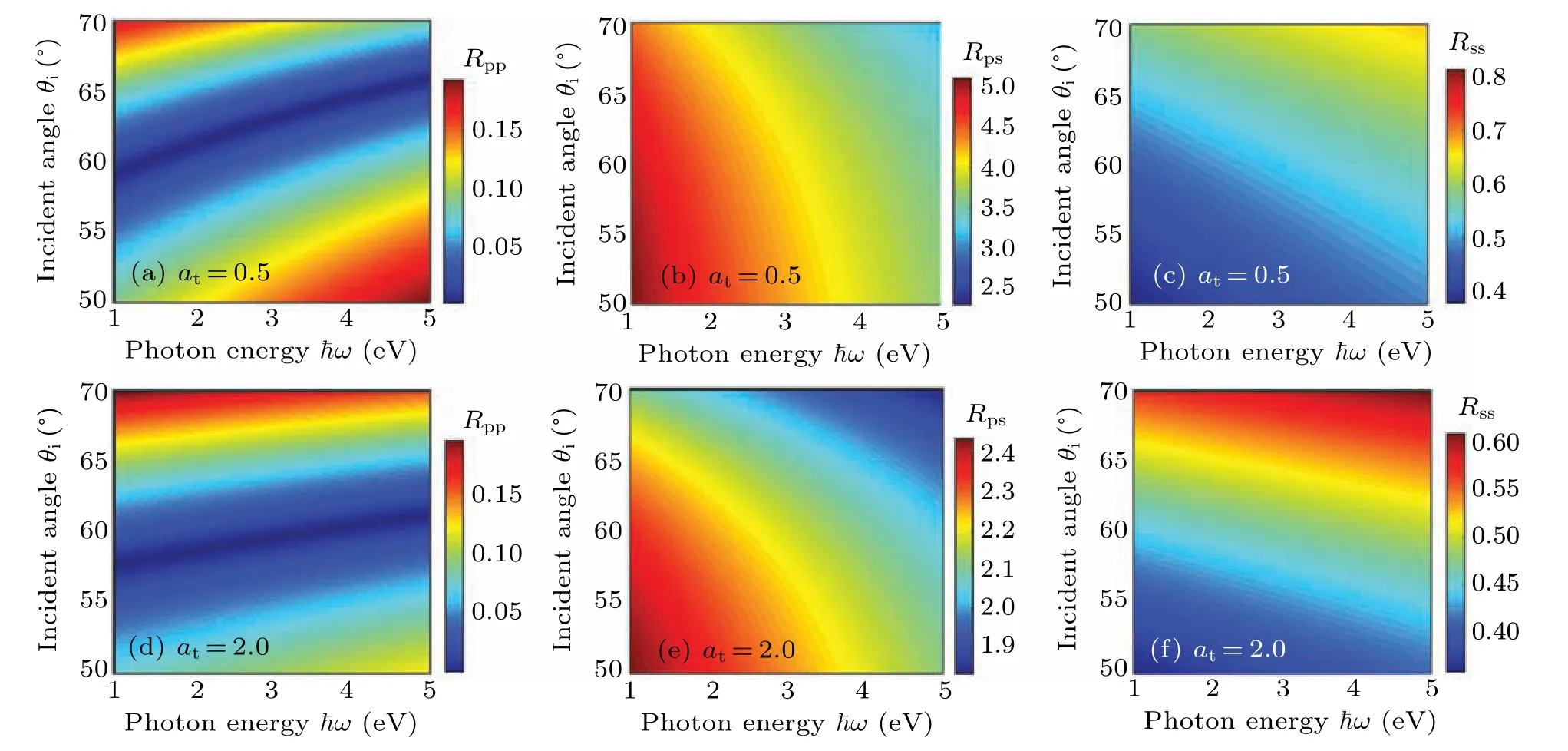
Fig.6. Pseudo-color images of modulus value of reflection coefficient Rpp，Rps，Rss as functions of photon energy ¯hω and the incident angles θi at Weyl cone tilting: (a)–(c)at=0.5(type-I WSMs)，(d)–(f)at=2.0(type-II WSMs). Chemical potential is chosen as μ =0.098 eV.

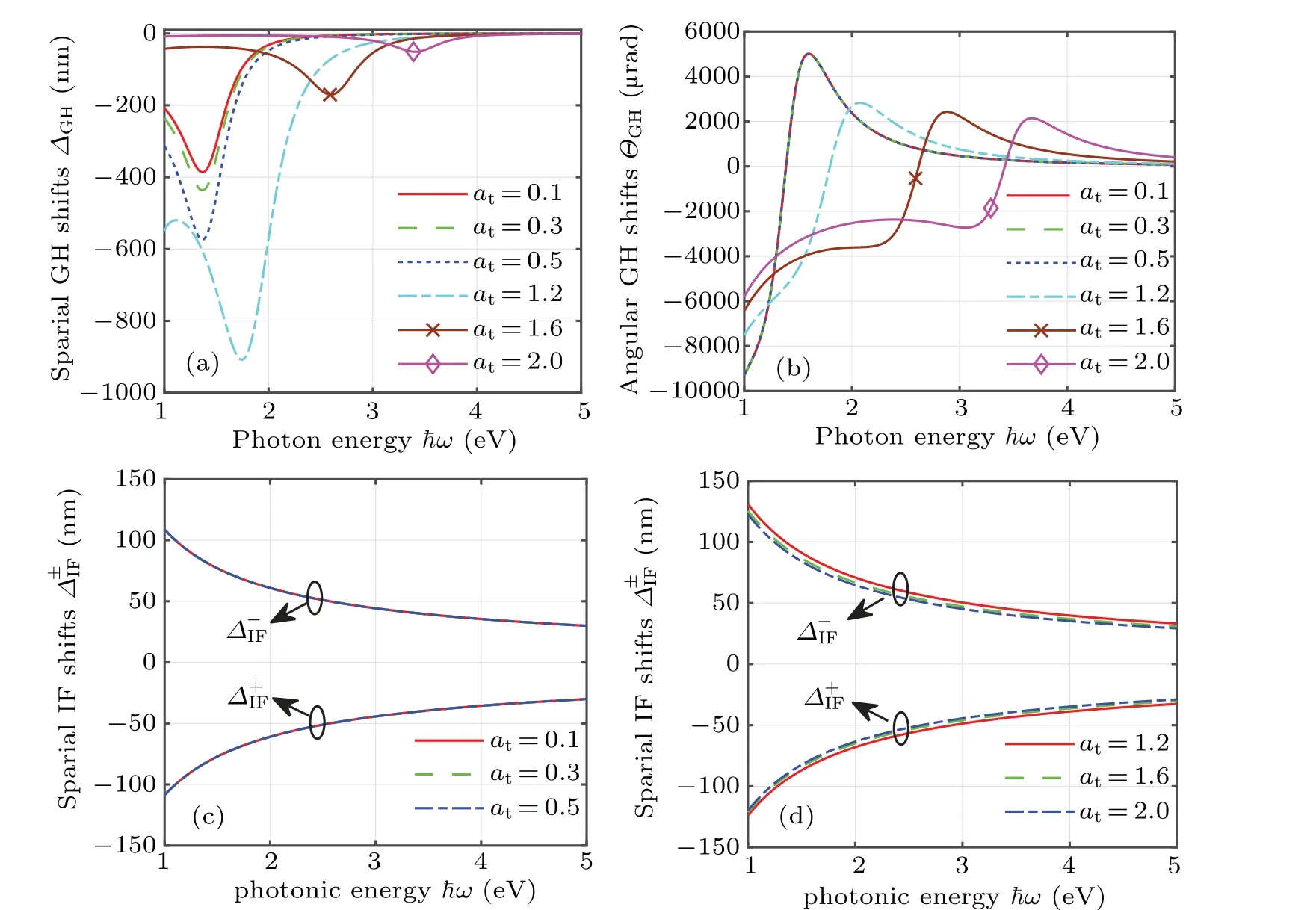
Fig.7. Dependences of GH and IF shifts on photon energy ¯hω at different Weyl cone tilting: (a)and(b)spatial GH shift ΔGH and angular GH shift ΔGH，respectively，(c)and(d)spatial IF shifts Δ±IF in type-I and type-II WSMs，respectively. Here+and-indicate left-and right-handed circular polarization correspondingly. The tilt degree are chosen as at =0.1，0.3，0.5 (type-I WSMs) and at =1.2，1.6，2.0 (type-II WSMs).Chemical potential is chosen as μ =0.098 eV.

The GH shifts [Figs. 7(a) and 7(b)] and IF shifts[Figs. 7(c) and 7(d)] are plotted as functions of photon energy at discrete tilt degrees ofat=0.1，0.3，0.5(type-I WSMs)andat=1.2，1.6，2.0 (type-II WSMs). It is obtained that GH spatial shifts increase to their peaks first and then gradually decrease with photon energy [Fig. 7(a)]. Notably， the positions of peak values in type-I WSMs almost keep stable because the Brewster angle does not change with Weyl cone tilting at this time， which fits with the description in Fig. 2(a). However，the positions of peak values in type-II WSMs vary obviously with Weyl cone tilting due to the changing Brewster angle illustrated in Fig.2(a). Moreover，the peak value of spatial GH shifts in type-I WSMs changes weakly while that in type-II WSMs decrease significantly with frequency. Similarly， we can obtain the variation rule of angular GH shifts with photon energy[Fig.7(b)]. The IF shifts for left-and right-handed circularly polarization incidences are of equal size and in the opposite directions，which gradually decrease with the frequency in both type-I WSMs[Fig.7(c)]and type-II WSMs[Fig.7(d)].Meanwhile， in the case of fixed frequency， the shifts are not dependent onatin type-I WSMs but change withatin type-II WSMs， as seen in ¯hω=1.96 eV. These trends are highly consistent with the tilt-dependent GH and IF shifts illustrated in Figs.3(a)–3(b)and 4(a)–4(b). In brief，our study can be extended to the study and application of tilt-dependent GH and IF shifts in tilted and doped WSMs， in the case of other frequency bands.

4. Conclusion

In summary， we have established the models to describe the GH and IF effects in tilted WSMs，and systematically studied the influences of Weyl cone tilting and chemical potential on the GH and IF shifts. The results show that the GH and IF shifts in tilted WSMs almost exhibit symmetry distribution relative to the Weyl cone tilting. The beam shifts in type-I WSMs are hardly dependent on Weyl cone tilting， while the shifts in type-II WSMs are very sensitive to the tilting. Meanwhile，there exists drastic changes of GH shifts in the boundary between type-I and type-II WSMs，where the peak value of GH spatial shift reaches up to-7589.66 nm，and the boundary and peak values can be manipulated significantly by adjusting chemical potential. The IF shifts are symmetric relative to the coordinate origin，whose symmetry axis produces an obvious relative offset with the variation of chemical potential.In addition，we have extended to discuss the influences of frequency on the GH and IF shifts. With the increase of frequency， the GH shifts occur with a peak fluctuation， and the IF shifts decrease gradually. Importantly， the change rule of beam shifts in two types of WSMs at any fixed frequency fits well with the case of photon energy 1.96 eV. Notice that IF shifts are generally too weak to be detected，which can be amplified and experimentally observed by introducing a weak signal amplification method called quantum weak measurement. The present study can provide a new reference to revisit the beam shifts in tilted WSMs and to determine the type of WSMs，and can provide a reference to research and applications of tilt-dependent GH and IF shifts in other frequency bands.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 62075060)， the Natural Science Foundation of Hunan Province (Grant No. 2020JJ4033)， the Research Foundation of Education Bureau of Hunan Province(Grant Nos. 20A218 and 19A198)， Science and Technology Plan Project of Hunan Province(Grant No.2019TP1014)，and the Hunan Province Innovation Foundation for Postgraduate Grant(Grant No.CX20211185).